kordaja meetodLagrange(ingliskeelses kirjanduses "LaGrange'i määramata kordajate meetod") ˗ see on arvuline meetod optimeerimisülesannete lahendamiseks, mis võimaldab määrata "tingimusliku" ekstreemumi objektiivne funktsioon(minimaalne või maksimaalne väärtus)

selle muutujatele antud piirangute olemasolul võrduste kujul (st pindala lubatud väärtused)

˗ need on funktsiooni argumendi väärtused (kontrollitud parameetrid) reaalalal, kus funktsiooni väärtus kaldub äärmusesse. Nime "tingimuslik" ekstreemum kasutamine on tingitud asjaolust, et muutujad on peale surutud lisatingimus, mis piirab funktsiooni äärmuse otsimisel lubatud väärtuste vahemikku.

Lagrange'i kordaja meetod võimaldab lubatavate väärtuste hulgast sihtfunktsiooni tingimusliku ekstreemumi leidmise probleemi teisendada funktsiooni tingimusteta optimeerimise probleemiks.

Kui funktsioonid Ja on pidevad koos nende osatuletistega, siis on muutujad λ, mis ei ole samaaegselt võrdsed nulliga, mille korral on täidetud järgmine tingimus:

Seega koostan vastavalt Lagrange'i kordajate meetodile sihtfunktsiooni ekstreemumi otsimiseks lubatavate väärtuste hulgast Lagrange'i funktsiooni L(x, λ), mida optimeeritakse veelgi:

kus λ ˗ on täiendavate muutujate vektor, mida nimetatakse määramatuteks Lagrange'i kordajateks.

Seega on funktsiooni f(x) tingimusliku ekstreemumi leidmise probleem taandatud funktsiooni L(x, λ) tingimusteta ekstreemumi leidmise probleemiks.

Ja

Lagrange'i funktsiooni ekstreemumi vajalik tingimus on antud võrrandisüsteemiga (süsteem koosneb "n + m" võrranditest):

Selle võrrandisüsteemi lahendus võimaldab määrata funktsiooni (X) argumendid, mille juures funktsiooni väärtus L(x, λ), samuti sihtfunktsiooni väärtus f(x) vastavad äärmus.

Lagrange'i kordajate (λ) väärtus pakub praktilist huvi, kui piirangud esitatakse võrrandi vaba liikmega (konstant) kujul. Sel juhul saame sihtfunktsiooni väärtust edasi kaaluda (suurendada/vähendada), muutes võrrandisüsteemis konstandi väärtust . Seega iseloomustab Lagrange'i kordaja sihtfunktsiooni maksimumi muutumise kiirust piirava konstandi muutumisega.

Saadud funktsiooni ekstreemumi olemuse määramiseks on mitu võimalust:

Esimene viis: Olgu - äärmuspunkti koordinaadid ja - sihtfunktsiooni vastav väärtus. Võetakse punkt, mis on punktile lähedal, ja arvutatakse sihtfunktsiooni väärtus:

Kui , siis on punktis maksimum.

Kui , siis on punktis miinimum.

Teine viis: Piisav tingimus, mille põhjal saab määrata ekstreemumi olemuse, on Lagrange'i funktsiooni teise diferentsiaali märk. Lagrange'i funktsiooni teine ​​diferentsiaal on defineeritud järgmiselt:

Kui sisse antud punkt miinimum, kui , siis on sihtfunktsioonil f(x) tingimuslik maksimaalselt.

Kolmas viis: Samuti saab funktsiooni ekstreemumi olemuse leida, võttes arvesse Lagrange'i funktsiooni Hessi. Hesseni maatriks on sümmeetriline ruutmaatriks funktsiooni teised osatuletised punktis, kus maatriksi elemendid on põhidiagonaali suhtes sümmeetrilised.

Ekstreemumi tüübi (funktsiooni maksimum või miinimum) määramiseks võite kasutada Sylvesteri reeglit:

1. Et Lagrange'i funktsiooni teine ​​diferentsiaal oleks positiivse märgiga on vajalik, et funktsiooni nurkmollid oleksid positiivsed. Sellistel tingimustel on sellel hetkel funktsioonil miinimum.

2. Et Lagrange'i funktsiooni teine ​​diferentsiaal oleks märginegatiivne , on vajalik, et funktsiooni nurkmollid vahelduksid ja maatriksi esimene element peab olema negatiivne sv . Sellistel tingimustel on funktsioonil antud hetkel maksimum.

Nurkmoll on moll, mis asub algmaatriksi esimeses k reas ja k veerus.

Peamine praktiline väärtus Lagrange'i meetod on see, et see võimaldab teil liikuda tingimuslikult optimeerimiselt tingimusteta ja vastavalt laiendada arsenali kättesaadavad meetodid probleemi lahendamine. Kuid võrrandisüsteemi lahendamise ülesanne, millele seda meetodit, üldiselt pole see lihtsam algne probleemäärmuslik otsing. Selliseid meetodeid nimetatakse kaudseteks. Nende kasutamine on seletatav vajadusega saada äärmuslikule probleemile lahendus analüütilises vormis (näiteks teatud teoreetiliste arvutuste jaoks). Kui käsitleda konkreetset praktilisi ülesandeid Tavaliselt kasutatakse otseseid meetodeid, mis põhinevad optimeeritavate funktsioonide väärtuste arvutamise ja võrdlemise iteratiivsetel protsessidel.

Arvutusmeetod

1 samm: Määrame Lagrange'i funktsiooni antud sihtfunktsioonist ja piirangute süsteemist:

Edasi

Artiklile kommentaari lisamiseks registreeruge saidil.

Parameetri nimi	Tähendus
Artikli teema:	Lagrange'i meetod.
Rubriik (temaatiline kategooria)	Matemaatika

Polünoomi leidmine tähendab selle koefitsiendi väärtuste määramist . Selleks saate interpolatsioonitingimust kasutades moodustada lineaarsete algebraliste võrrandite süsteemi (SLAE).

Selle SLAE determinanti nimetatakse tavaliselt Vandermonde determinandiks. Vandermonde determinant ei ole null for for , st juhul, kui otsingutabelis pole ühtegi sobivat sõlme. Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, võib väita, et SLAE-l on lahendus ja see lahendus on ainulaadne. SLAE lahendamine ja tundmatute koefitsientide määramine saab konstrueerida interpolatsioonipolünoomi.

Polünoom, mis vastab interpolatsiooni tingimustele, kui seda interpoleeritakse Lagrange'i meetodil, konstrueeritakse n-nda astme polünoomide lineaarse kombinatsioonina:

Polünoomideks nimetatakse põhilised polünoomid. Selleks, et Lagrange'i polünoom täidab interpolatsiooni tingimusi, on äärmiselt oluline, et selle põhipolünoomide jaoks oleksid täidetud järgmised tingimused:

Sest .

Kui need tingimused on täidetud, on meil kõigil:

Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, põhipolünoomide etteantud tingimuste täitmine tähendab, et ka interpolatsioonitingimused on täidetud.

Määrakem põhipolünoomide kuju neile seatud piirangute alusel.

1. tingimus: aadressil .

2. tingimus: .

Lõpuks võime põhipolünoomi jaoks kirjutada:

Seejärel asendades saadud avaldise põhipolünoomide jaoks algse polünoomiga, saame Lagrange'i polünoomi lõpliku vormi:

privaatne vorm Lagrange'i polünoomi at nimetatakse tavaliselt lineaarseks interpolatsiooni valemiks:

.

Punktis võetud Lagrange'i polünoomi nimetatakse tavaliselt ruutinterpolatsiooni valemiks:

Lagrange'i meetod. - mõiste ja liigid. Kategooria "Lagrange'i meetod" klassifikatsioon ja omadused. 2017, 2018.

- Lagrange'i meetod (suvalise konstandi muutmise meetod).

Lineaarsed kaugjuhtimispuldid. Definitsioon. tüübikontroll st. lineaarne tundmatu funktsiooni ja selle tuletise suhtes nimetatakse lineaarseks. Seda tüüpi lahenduse jaoks on ur-th kaks meetodit: Lagrange'i meetod ja Bernoulli meetod. Vaatleme homogeenset DE-d.

- Lineaarne kaugjuhtimispult, homogeenne ja heterogeenne. Üldlahenduse kontseptsioon. Lagrange'i meetod konstantide korrutiste muutmiseks.

Definitsioon. DU nimetatakse homogeenseks, kui f-i saab esitada kui f-i nende argumentide suhtes Näide. F-Mind kutsutakse homogeenseks f-s mõõtmine kui Näited: 1) - 1. järku homogeensus. 2) - 2. homogeensuse järjekord. 3) - homogeensuse nulljärk (lihtsalt homogeenne... .

- Loeng 8. Osatuletiste rakendamine: ekstreemumi ülesanded. Lagrange'i meetod.

Ekstreemsed ülesanded on suur tähtsus majanduslikes arvutustes. See on näiteks maksimaalse tulu, kasumi, minimaalsete kulude arvutamine, mis sõltub mitmest muutujast: ressursid, tootmisvarad jne. Funktsioonide ekstreemumite leidmise teooria... .

- T.2.3. DE kõrgemate tellimuste kohta. Võrrand summaarsetes diferentsiaalides. T.2.4. Teist järku lineaarne DE konstantsete koefitsientidega. Lagrange'i meetod.

3. 2. 1. DE eraldatavate muutujatega S.R. 3. Loodusteadustes, tehnoloogias ja majanduses tuleb sageli tegeleda empiiriliste valemitega, s.t. statistiliste andmete töötlemise põhjal koostatud valemid või ...

Tingimusliku ekstreemumi määramise meetod algab konstruktsioonist abistaja funktsioon Lagrange, mis saavutab teostatavate lahenduste piirkonnas maksimumi samade muutujate väärtuste korral x 1 , x 2 , ..., x n , mis on sihtfunktsioon z . Olgu probleemiks funktsiooni tingimusliku ekstreemumi määramine z=f(X) piirangute all φ i ( x 1 , x 2 , ..., x n ) = 0, i = 1, 2, ..., m , m < n

Koostage funktsioon

mida nimetatakse Lagrange'i funktsioon. X , - konstantsed tegurid ( Lagrange'i kordajad). Pange tähele, et Lagrange'i kordajaid saab anda majanduslik mõte. Kui f(x 1 , x 2 , ..., x n ) - tulu vastavalt plaanile X = (x 1 , x 2 , ..., x n ) ja funktsioon φ i (x 1 , x 2 , ..., x n ) on sellele plaanile vastava i-nda ressursi kulud, siis X , - i-nda ressursi hind (hinnang), mis iseloomustab sihtfunktsiooni äärmise väärtuse muutust sõltuvalt i-nda ressursi suuruse muutusest (marginaalne hinnang). L(X) - funktsioon n+m muutujad (x 1 , x 2 , ..., x n , λ 1 , λ 2 , ..., λ n ) . Selle funktsiooni statsionaarsete punktide määramine viib võrrandisüsteemi lahendamiseni

Seda on lihtne näha . Seega funktsiooni tingliku ekstreemumi leidmise probleem z=f(X) taandub funktsiooni lokaalse ekstreemumi leidmisele L(X) . Kui statsionaarne punkt leitakse, siis lahendatakse ekstreemumi olemasolu küsimus kõige lihtsamatel juhtudel ekstreemumi jaoks piisavate tingimuste alusel - teise diferentsiaali märgi uurimine. d 2 L(X) statsionaarses punktis tingimusel, et muutuja suureneb Δx i - seotud suhetega

mis saadakse piiranguvõrrandite diferentseerimisel.

Kahe tundmatuga mittelineaarsete võrrandite süsteemi lahendamine Solver tööriista abil

Seadistamine Lahenduse leidmine võimaldab leida lahenduse kahe tundmatuga mittelineaarsete võrrandite süsteemile:

Kus
- muutujate mittelineaarne funktsioon x Ja y ,
on suvaline konstant.

On teada, et paar x , y ) on võrrandisüsteemi (10) lahend siis ja ainult siis, kui see on järgmise võrrandi lahend kahes tundmatus:

KOOS teisest küljest on süsteemi (10) lahendus kahe kõvera lõikepunktid: f ] (x, y) = C Ja f 2 (x, y) = C 2 pinnal XOY.

Sellest tuleneb meetod süsteemi juurte leidmiseks. mittelineaarsed võrrandid:

Määrake (vähemalt ligikaudne) võrrandisüsteemi (10) või võrrandi (11) lahendi olemasolu intervall. Siin tuleb arvesse võtta süsteemis sisalduvate võrrandite tüüpi, nende iga võrrandi definitsioonipiirkonda jne. Mõnikord kasutatakse lahenduse esialgse lähenduse valikut;

Koostage valitud intervallil muutujate x ja y võrrandi (11) lahendus või koostage funktsioonide graafikud f 1 (x, y) = C ja f 2 (x, y) = C 2 (süsteem(10)).

Lokaliseerige võrrandisüsteemi väidetavad juured - leidke mitu minimaalsed väärtused koostage tabelist võrrandi (11) juured või määrake süsteemi (10) sisalduvate kõverate lõikepunktid.

4. Leidke lisandmooduli abil võrrandisüsteemi (10) juured Otsige lahendust.

Lagrange'i kordajate meetod.

Lagrange'i kordaja meetod on üks meetoditest, mis võimaldab probleeme mitte lahendada lineaarne programmeerimine.

Mittelineaarne programmeerimine on matemaatilise programmeerimise haru, mis uurib meetodeid äärmuslike probleemide lahendamiseks mittelineaarse sihtfunktsiooniga ja mittelineaarsete piirangutega määratletud teostatavate lahenduste valdkonnaga. Majandusteaduses vastab see asjaolule, et tulemused (efektiivsus) suurenevad või vähenevad ebaproportsionaalselt ressursikasutuse ulatuse (või samaväärselt tootmismahu) muutustega: näiteks ettevõtete tootmiskulude jagamise tõttu muutujateks. ja tinglikult konstandid; kaupade nõudluse küllastumise tõttu, kui iga järgnevat üksust on raskem müüa kui eelmist jne.

Mittelineaarse programmeerimise probleem püstitatakse kui teatud sihtfunktsiooni optimumi leidmise probleem

F(x 1 ,…x n), F (x) → max

tingimustel

g j (x 1,…x n)≥0, g (x) ≤ b , x ≥ 0

Kus x-vajalike muutujate vektor;

F (x) -objektiivfunktsioon;

g (x) on piirangufunktsioon (pidevalt diferentseeritav);

b - kitsenduskonstantide vektor.

Mittelineaarse programmeerimisülesande lahendus (globaalne maksimum või miinimum) võib kuuluda kas lubatava hulga piiridesse või sisemusse.

Vastupidiselt lineaarsele programmeerimisprobleemile ei ole mittelineaarse programmeerimisülesande puhul optimaalne tingimata piirangutega määratletud piirkonna piiril. Teisisõnu, probleemiks on selliste muutujate mittenegatiivsete väärtuste valimine, mis sõltuvad ebavõrdsuste kujul olevate piirangute süsteemist, mille korral saavutatakse antud funktsiooni maksimum (või miinimum). Sel juhul ei sätestata ei sihtfunktsiooni ega ebavõrdsuse vorme. Võib olla erinevad juhtumid: sihtfunktsioon on mittelineaarne ja piirangud on lineaarsed; sihtfunktsioon on lineaarne ja piirangud (vähemalt üks neist) on mittelineaarsed; nii sihtfunktsioon kui ka piirangud on mittelineaarsed.

Mittelineaarse programmeerimise probleem esineb loodusteadustes, inseneriteaduses, majanduses, matemaatikas, ärisuhetes ja riigiteadustes.

Näiteks mittelineaarne programmeerimine on seotud põhilisega majanduslik ülesanne. Nii et jaotusprobleemis piiratud ressursid maksimeerida kas tõhusust või, kui tarbijat uuritakse, tarbimist piirangute alusel, mis väljendavad ressursside nappuse tingimusi. Sellise üldsõnastuse puhul võib ülesande matemaatiline sõnastamine osutuda võimatuks, kuid konkreetsetes rakendustes saab kõikide funktsioonide kvantitatiivse vormi otse määrata. Näiteks toodab tööstusettevõte plasttooteid. Tootmise efektiivsust mõõdetakse siin kasumiga ja piiranguid tõlgendatakse kui saadaolevat tööjõudu, tootmispinda, seadmete tootlikkust jne.

"Tasuvuse" meetod sobib ka mittelineaarse programmeerimise skeemi. See meetod töötati välja valitsuse otsuste tegemisel. Üldfunktsioon tõhusus on heaolu. Siin kerkivad esile kaks mittelineaarse programmeerimise probleemi: esimene on efekti maksimeerimine piiratud kuludega, teine ​​on kulude minimeerimine eeldusel, et mõju on üle teatud miinimumtaseme. See probleem on tavaliselt hästi modelleeritud, kasutades mittelineaarset programmeerimist.

Mittelineaarse programmeerimise probleemi lahendamise tulemused on abiks valitsuse otsuste tegemisel. Saadud lahendus on loomulikult soovitatav, mistõttu on enne lõpliku otsuse tegemist vaja uurida mittelineaarse programmeerimisülesande sõnastuse eeldusi ja täpsust.

Mittelineaarsed ülesanded on keerulised, sageli lihtsustatakse neid lineaarsete probleemidega. Selleks eeldatakse tinglikult, et konkreetses piirkonnas sihtfunktsioon suureneb või väheneb võrdeliselt sõltumatute muutujate muutumisega. Seda lähenemist nimetatakse osade kaupa lineaarsete lähenduste meetodiks, kuid see on rakendatav ainult teatud tüüpi mittelineaarsete probleemide korral.

Mittelineaarsed ülesanded teatud tingimustel lahendatakse Lagrange'i funktsiooni abil: olles leidnud selle sadulapunkti, leiavad nad ka ülesande lahenduse. Arvutusalgoritmide hulgas N. p. tore koht hõivata gradiendi meetodeid. Mittelineaarsete probleemide jaoks pole universaalset meetodit ja ilmselt ei pruugi ka olla, kuna need on äärmiselt mitmekesised. Multi-äärmuslikke probleeme on eriti raske lahendada.

Üks meetoditest, mis võimaldab taandada mittelineaarse programmeerimise probleemi võrrandisüsteemi lahendamiseks, on meetod määramatud kordajad Lagrange.

Lagrange'i kordaja meetodi abil tehakse sisuliselt kindlaks vajalikud tingimused, mis võimaldab tuvastada optimeerimisprobleemide optimaalseid punkte piirangute kujul võrdsuste kujul. Sel juhul muudetakse piirangutega seotud probleem samaväärseks piiramatu optimeerimise probleemiks, milles ilmnevad mõned tundmatud parameetrid, mida nimetatakse Lagrange'i kordajateks.

Lagrange'i kordaja meetod seisneb tingimusliku ekstreemumi probleemide taandamises abifunktsiooni tingimusteta ekstreemumi probleemideks - nn. Lagrange'i funktsioonid.

Funktsiooni ekstreemumi probleemi jaoks f(x 1, x 2,..., x n) tingimustel (sidustamisvõrrandid) φ i(x 1 , x 2 , ..., x n) = 0, i= 1, 2,..., m, on Lagrange'i funktsioonil vorm

L(x 1, x 2… x n, λ 1, λ 2,… λm)=f(x 1, x 2… x n)+∑ i -1 m λ i φ i (x 1, x 2… x n)

Kordajad λ 1 , λ 2 , ..., λm helistas Lagrange'i kordajad.

Kui kogused x 1 , x 2 , ..., x n , λ 1 , λ 2 , ..., λm on Lagrange'i funktsiooni statsionaarseid punkte määravate võrrandite lahendid, nimelt diferentseeruvate funktsioonide puhul on need võrrandisüsteemi lahendid

siis piisavalt üldistel eeldustel x 1 , x 2 , ..., x n esitab funktsiooni f ekstreemumi.

Mõelge n muutuja funktsiooni minimeerimise probleemile, võttes arvesse üht piirangut võrdsuse kujul:

Minimeeri f(x 1, x 2… x n) (1)

piirangutega h 1 (x 1, x 2… x n)=0 (2)

Kooskõlas Lagrange'i kordaja meetodiga muudetakse see probleem järgmiseks piiramatuks optimeerimise probleemiks:

minimeerida L(x,λ)=f(x)-λ*h(x) (3)

kus funktsiooni L(х;λ) nimetatakse Lagrange'i funktsiooniks,

λ on tundmatu konstant, mida nimetatakse Lagrange'i kordajaks. λ märgile ei esitata mingeid nõudeid.

Laske kl seatud väärtusλ=λ 0 funktsiooni L(x,λ) tingimusteta miinimum x suhtes saavutatakse punktis x=x 0 ja x 0 rahuldab võrrandi h 1 (x 0)=0. Siis, nagu on lihtne näha, minimeerib x 0 (1), võttes arvesse (2), kuna kõigi x väärtuste korral, mis rahuldavad (2), h 1 (x)=0 ja L(x,λ)= min f(x).

Loomulikult on vaja valida väärtus λ=λ 0 nii, et tingimusteta miinimumpunkti x 0 koordinaat rahuldaks võrdsust (2). Seda saab teha siis, kui λ muutujana arvesse võttes leiame funktsiooni (3) tingimusteta miinimumi funktsiooni λ kujul ja seejärel valime λ väärtuse, mille korral võrdus (2) on täidetud. Illustreerime seda konkreetse näitega.

Minimeerige f(x)=x 1 2 +x 2 2 =0

piiranguga h 1 (x) = 2x 1 +x 2 -2 = 0 = 0

Vastav piiramatu optimeerimise probleem on kirjutatud järgmiselt:

minimeerida L(x,λ)=x 1 2 +x 2 2 -λ(2x 1 +x 2 -2)

Lahendus. Võrdsustades gradiendi L kaks komponenti nulliga, saame

→ x 1 0 =λ

→ x 2 0 =λ/2

Kontrollimaks, kas statsionaarne punkt x° vastab miinimumile, arvutame välja funktsiooni L(x; u) Hessi maatriksi elemendid, mida vaadeldakse x funktsioonina,

mis osutub positiivseks kindlaks.

See tähendab, et L(x, u) on x-i kumerfunktsioon. Seetõttu määravad koordinaadid x 1 0 =λ, x 2 0 =λ/2 globaalse miinimumpunkti. Optimaalne väärtusλ leitakse asendades väärtused x 1 0 ja x 2 0 võrrandis 2x 1 +x 2 =2, millest 2λ+λ/2=2 või λ 0 =4/5. Seega saavutatakse tingimuslik miinimum x 1 0 =4/5 ja x 2 0 =2/5 ning on võrdne min f(x)=4/5.

Näite põhjal ülesande lahendamisel käsitlesime L(x; λ) kahe muutuja x 1 ja x 2 funktsioonina ning lisaks eeldasime, et parameetri λ väärtus on valitud nii, et piirang on täidetud. Kui süsteemi lahendus

J = 1,2,3,…,n

ei saa saada λ eksplitsiitsete funktsioonide kujul, siis leitakse x ja λ väärtused, lahendades järgmise süsteemi, mis koosneb n + 1 võrrandist n + 1 tundmatuga:

J = 1,2,3,…,n., h1 (x) = 0

Et kõik üles leida võimalikud lahendused Selle süsteemi puhul saate kasutada numbrilisi otsingumeetodeid (näiteks Newtoni meetodit). Iga lahenduse () jaoks tuleks arvutada funktsiooni L Hessi maatriksi elemendid, mida vaadeldakse kui funktsiooni x, ja välja selgitada, kas see maatriks on positiivne kindel (lokaalne miinimum) või negatiivne kindel (kohalik maksimum). ).

Lagrange'i kordajate meetodit saab laiendada ka juhul, kui ülesandel on mitu piirangut võrduste näol. Mõelge üldisele probleemile, mis nõuab

Minimeeri f(x)

piirangute all h k =0, k=1, 2, ..., K.

Lagrange'i funktsioon võtab järgmine vaade:

Siin λ 1 , λ 2 , ..., λk-Lagrange'i kordajad, st. tundmatud parameetrid, mille väärtused tuleb määrata. Võrdsustades L osatuletised x suhtes nulliga, saame järgmine süsteem n võrrand n tundmatuga:

Kui ülaltoodud süsteemile osutub keeruliseks lahenduse leidmine vektori λ funktsioonide näol, siis on võimalik süsteemi laiendada, lisades piiranguid võrduste kujul

Laiendatud süsteemi lahendus, mis koosneb n + K võrrandist, milles on n + K tundmatuid, määrab funktsiooni L statsionaarse punkti. Seejärel rakendatakse miinimumi või maksimumi kontrollimise protseduur, mis viiakse läbi arvutamise alusel. funktsiooni L Hessi maatriksi elemendid, mida vaadeldakse x funktsioonina, sarnaselt sellele, mida tehti ühe piiranguga ülesande puhul. Mõne probleemi puhul ei pruugi n+K tundmatutega n+K võrrandite laiendatud süsteemil lahendusi olla ja Lagrange'i kordaja meetod osutub mittekasutatavaks. Siiski tuleb märkida, et sellised ülesanded on praktikas üsna haruldased.

Kaaluge erijuhtum ühine ülesanne mittelineaarne programmeerimine, eeldades, et piirangute süsteem sisaldab ainult võrrandeid, puuduvad tingimused muutujate mittenegatiivsuseks ja ja - funktsioonid on pidevad koos nende osatuletistega. Seega, pärast võrrandisüsteemi (7) lahendamist saadakse kõik punktid, mille juures funktsioonil (6) võivad olla äärmuslikud väärtused.

Lagrange'i kordajate meetodi algoritm

1. Koostame Lagrange'i funktsiooni.

2. Leiame Lagrange'i funktsiooni osatuletised muutujate x J ,λ i suhtes ja võrdsustame need nulliga.

3. Lahendame võrrandisüsteemi (7), leiame punktid, kus ülesande sihtfunktsioonil võib olla ekstreemum.

4. Ekstreemumi kahtlaste punktide hulgast leiame need, kus ekstreemumi saavutatakse, ja arvutame nendes punktides funktsiooni (6) väärtused.

Näide.

Algandmed: Tootmisplaani kohaselt on ettevõttel vaja toota 180 toodet. Neid tooteid saab valmistada kahel tehnoloogilisel viisil. 1. meetodi x 1 toote valmistamisel on kulud 4x 1 + x 1 2 rubla ja 2. meetodi x 2 toote valmistamisel on need 8x 2 + x 2 2 rubla. Määrake, mitu toodet tuleks iga meetodiga valmistada, et tootmiskulud oleksid minimaalsed.

Probleemi eesmärgifunktsioonil on vorm
® min tingimustes x 1 +x 2 =180, x 2 ≥0.
1. Koostage funktsioon Lagrange
.
2. Arvutame osatuletised x 1, x 2, λ suhtes ja võrdsustame need nulliga:

3. Lahendades saadud võrrandisüsteemi, leiame x 1 \u003d 91, x 2 \u003d 89

4. Olles sihtfunktsioonis x 2 \u003d 180-x 1 asendanud, saame ühe muutuja funktsiooni, nimelt f 1 \u003d 4x 1 +x 1 2 +8 (180-x 1) + (180- x 1) 2

Arvuta või 4x1 -364=0 ,

kust meil on x 1 * =91, x 2 * =89.

Vastus: Esimese meetodiga toodetud toodete arv on x 1 \u003d 91, teise meetodiga x 2 \u003d 89, samas kui sihtfunktsiooni väärtus on 17278 rubla.

• õpetus

Kõik head päeva. Selles artiklis tahan näidata ühte neist graafilised meetodid hoone matemaatilised mudelid dünaamiliste süsteemide jaoks, mida nimetatakse sidemete graafik("side" - ühendused, "graafik" - graafik). Vene kirjandusest leidsin selle meetodi kirjeldusi ainult Tomski Polütehnilise Ülikooli õpikust A.V. Voronin "MEHHATROONILISTE SÜSTEEMIDE MODELLEERIMINE" 2008. Näidake ka klassikalist meetodit läbi Lagrange'i võrrandi 2. tüüpi.

Lagrange'i meetod

Teooriat ma maalima ei hakka, näitan arvutuste etappe ja paari kommentaariga. Mulle isiklikult on lihtsam näidetest õppida, kui teooriat 10 korda läbi lugeda. Mulle tundus, et vene kirjanduses on selle meetodi ja matemaatika või füüsika seletused väga rikkalikud. keerulised valemid, mis nõuab vastavalt tõsist matemaatilist tausta. Lagrange’i meetodit õppides (õppides Itaalias Torino Polütehnilises Ülikoolis) õppisin arvutusmeetodite võrdlemiseks vene kirjandust ja selle meetodi lahendamise edenemist oli mul raske jälgida. Isegi Harkovi Lennuinstituudi modelleerimiskursusi meenutades oli selliste meetodite tuletamine väga tülikas ja keegi ei vaevunud sellest küsimusest aru saama. Selle otsustasin kirjutada, Lagrange'i järgi mattide mudelite ehitamise juhendi, nagu selgus, pole see sugugi keeruline, piisab, kui teada, kuidas arvutada ajatuletisi ja osatuletisi. Keerulisemate mudelite jaoks on lisatud rotatsioonimaatriksid, kuid ka neis pole midagi keerulist.

Modelleerimismeetodite omadused:

• Newton Euler: dünaamilisel tasakaalul põhinevad vektorvõrrandid jõud (jõud) Ja hetked
• Lagrange: skalaarvõrrandid, mis põhinevad kineetika ja potentsiaaliga seotud olekufunktsioonidel energiat
• sidemete graafik: voolupõhine meetod võimsus (võimsus) süsteemi elementide vahel

Alustame sellest lihtne näide. Kaal koos vedru ja siibriga. Jätame tähelepanuta gravitatsioonijõu.

Joonis 1. Kaal koos vedru ja siibriga

Kõigepealt määratleme:

• esialgne süsteem koordinaadid(NSK) või fikseeritud sk R0(i0,j0,k0). Kuhu? Võite näpuga taevasse pista, kuid ajus olevate neuronite otste tõmblemisel läheb mõte panna NSC M1 keha liikumisjoonele.
• iga massiga keha koordinaatsüsteemid(meil on M1 R1(i1,j1,k1)), orientatsioon võib olla meelevaldne, kuid milleks oma elu keerulisemaks teha, me määrame selle minimaalse erinevusega NSC-st
• üldistatud koordinaadid q_i(minimaalne muutujate arv, mis võib liikumist kirjeldada), in see näideüks üldistatud koordinaat, liikumine ainult mööda j-telge

Joonis 2. Koordinaatsüsteemide ja üldistatud koordinaatide ülespanemine

Joonis 3. Keha asend ja kiirus M1

Pärast seda, kui leiame siibri kineetilise (C) ja potentsiaalse (P) energia ning dissipatiivse funktsiooni (D) vastavalt valemitele:

Joonis 4. Täielik valem kineetiline energia

Meie näites pole pöörlemist, teine ​​komponent on 0.

Joonis 5. Kineetilise, potentsiaalse energia ja dissipatiivse funktsiooni arvutamine

Lagrange'i võrrandil on järgmine vorm:

Joonis 6. Lagrange'i võrrand ja Lagrange'i võrrand

Delta W_i See virtuaalne töö täiustatud rakendatud jõudude ja hetkedega. Leiame selle üles:

Joonis 7. Virtuaalse töö arvutamine

Kus delta q_1 virtuaalne liikumine.

Asendame kõik Lagrange'i võrrandisse:

Joonis 8. Saadud massimudel vedru ja siibriga

Siin lõppes Lagrange'i meetod. Nagu näete, pole see nii keeruline, kuid see on siiski väga lihtne näide, mille jaoks Newton-Euleri meetod oleks suure tõenäosusega isegi lihtsam. Keerulisemate süsteemide puhul, kus mitu keha on pööratud üksteise suhtes erinevate nurkade all, on Lagrange'i meetod lihtsam.

Bondi meetod graafik

Näitan teile kohe, kuidas mudel välja näeb sidegraafikul, näiteks vedru ja siibri massiga:

Joonis 9. Ühendusgraafiku mass vedru ja siibriga

Siin tuleb rääkida veidi teooriat, mille ehitamiseks piisab lihtsad mudelid. Kui kedagi huvitab, võib raamatut lugeda ( Võlakirjade graafik metoodika) või ( Voronin A.V. Mehhatrooniliste süsteemide modelleerimine: õpetus. - Tomsk: Tomski Polütehnilise Ülikooli kirjastus, 2008).

Esmalt määratleme selle keerulised süsteemid koosneb mitmest domeenist. Näiteks koosneb elektrimootor elektrilistest ja mehaanilistest osadest või domeenidest.

sidemete graafik põhineb nende domeenide, alamsüsteemide vahelisel energiavahetusel. Pange tähele, et mis tahes vormis elektrivahetus määratakse alati kahe muutujaga ( muutuv võimsus), mille abil saame uurida erinevate alamsüsteemide koostoimet dünaamilise süsteemi osana (vt tabel).

Nagu tabelist näha, on võimsuse väljendus kõikjal peaaegu sama. Kokkuvõttes, Võimsus- See töö " vool - f" peal " jõupingutused – e».

Pingutus(Inglise) pingutus) elektrivaldkonnas on see pinge (e), mehaanilises valdkonnas on see jõud (F) või moment (T), hüdraulikas on see rõhk (p).

Voolu(Inglise) voolu) elektrilises valdkonnas on see vool (i), mehaanilises valdkonnas on see kiirus (v) või nurkkiirus (oomega), hüdraulikas on see vool või vedeliku vool (Q).

Võttes need tähistused, saame võimsuse avaldise:

Joonis 10. Võimsuse valem võimsusmuutujate kujul

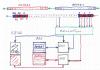
Seostegraafiku keeles on kahe võimsust vahetava alamsüsteemi vaheline seos kujutatud sidemega. võlakiri). Seetõttu nimetatakse seda meetodit sidemete graafik või g raf-ühendused, ühendatud graafik. Kaaluge plokkskeem sidemed elektrimootoriga mudelis (see pole veel sidegraafik):

Joonis 11. Domeenidevahelise võimsusvoo plokkskeem

Kui meil on pingeallikas, siis vastavalt genereerib see pinge ja annab selle tagasikerimiseks mootorile (seetõttu on nool suunatud mootori poole), olenevalt mähise takistusest tekib Ohmi seaduse järgi vool (suunatud mootor allikani). Sellest lähtuvalt on üks muutuja alamsüsteemi sisend ja teine ​​peab olema vajalik. tee välja allsüsteemist. Siin on pinge ( pingutus) – sisend, vool ( voolu) – väljumine.

Kui kasutate vooluallikat, kuidas diagramm muutub? Õige. Vool suunatakse mootorisse ja pinge allikasse. Siis praegune ( voolu) - Sisendpinge ( pingutus) – väljumine.

Vaatleme mehaanika näidet. Massile mõjuv jõud.

Joonis 12. Massile rakendatud jõud

Plokkskeem on järgmine:

Joonis 13. plokkskeem

Selles näites Strength ( pingutus) on massi sisendmuutuja. (massile rakendatud jõud)
Newtoni teise seaduse järgi:

Mass reageerib kiirusega:

Selles näites, kui üks muutuja ( jõudu - pingutus) on sissepääs mehaanilisse domeeni, seejärel teise võimsusmuutuja ( kiirust - voolu) - muutub automaatselt tee välja.

Selleks, et eristada, kus on sisend ja kus on väljund, kasutatakse vertikaalne joon elementide vahelise noole (ühenduse) lõpus nimetatakse seda joont põhjuslikkuse märk või põhjuslikkus (põhjuslikkus). Selgub: rakendatav jõud on põhjus ja kiirus on tagajärg. See märk on süsteemimudeli õigeks konstrueerimiseks väga oluline, kuna põhjuslikkus on kahe alamsüsteemi füüsilise käitumise ja jõuvahetuse tagajärg, mistõttu ei saa põhjuslikkuse märgi asukoha valik olla meelevaldne.

Joonis 14. Põhjuslikkuse märkimine

See vertikaalne joon näitab, milline alamsüsteem võtab vastu jõudu ( pingutus) ja selle tulemusena tekitavad voolu ( voolu). Massinäites näeks see välja järgmine:

Joonis 14. Massile mõjuva jõu põhjuslikkus

Noole järgi on selge, et massi sisend - jõudu, ja väljund on kiirust. Seda tehakse selleks, et mitte risustada näidishoone skeemi ja süstematiseerimist nooltega.

Edasi oluline punkt. Üldine hoog(liikumise hulk) ja liigub(energia muutujad).

Võimsuse ja energia muutujate tabel erinevates valdkondades

Ülaltoodud tabelis on toodud kaks täiendavat füüsikalist suurust, mida kasutatakse sidegraafiku meetodil. Neid kutsutakse üldistatud hoog (R) Ja üldine nihe (q) või energiamuutujaid ning neid saab saada võimsusmuutujate integreerimisel aja jooksul:

Joonis 15. Võimsuse ja energia muutujate vaheline seos

Elektrivaldkonnas :

Faraday seaduse järgi Pinge juhi otstes on võrdne seda juhti läbiva magnetvoo tuletisega.

A Praegune tugevus - füüsiline kogus, mis on võrdne mõne aja t läbi juhi ristlõike läbinud laengu Q ja selle ajaintervalli väärtuse suhtega.

Mehaaniline domeen:

Newtoni 2. seadusest, Jõud on impulsi aja tuletis

Ja vastavalt kiirust- nihke aja tuletis:

Teeme üldistuse:

Põhielemendid

Kõik elemendid sees dünaamilised süsteemid, saab jagada kahe- ja neljapooluselisteks komponentideks.
Kaaluge bipolaarsed komponendid:

Allikad
Allikad on nii pingutus kui ka vool. Analoogia elektrivaldkonnas: pingutuste allikas – pingeallikas, vooluallikas – praegune allikas. Allikate põhjuslikud märgid peaksid olema ainult sellised.

Joonis 16. Põhjuslikud seosed ja allikate määramine

R komponent – dissipatiivne element

Komponent I - inertsiaalne element

Komponent C - mahtuvuslik element

Nagu joonistelt näha, erinevaid elementeüks tüüp R,C,I kirjeldatakse samade võrranditega. Erinevus on AINULT elektrilise mahtuvuse osas, see tuleb lihtsalt meeles pidada!

Neljapooluse komponendid:

Mõelge kahele komponendile: trafo ja güraator.

viimane olulised komponendidühendused on sidegraafiku meetodil. Sõlme on kahte tüüpi:

See on komponentide lõpp.

Peamised sammud põhjuslike seoste tuvastamiseks pärast sidegraafiku koostamist:

1. Pange kõigele põhjuslikkus allikatest
2. Käige läbi kõik sõlmed ja pange pärast punkti 1 üles põhjuslikud seosed
3. Sest komponendid I määrata sisend põhjuslikkus (pingutus sisaldub selles komponendis), jaoks komponendid C määrata väljundi põhjuslik seos (pingutus tuleb sellest komponendist)
4. Korrake punkti 2
5. Joonistage põhjuslikud seosed R komponendid

Sellega on teooria minikursus lõpetatud. Nüüd on meil olemas kõik, mida vajame mudelite ehitamiseks.
Lahendame paar näidet. Alustame sellest elektriahel, on parem mõista sidegraafiku koostamise analoogiat.

Näide 1

Alustame pingeallikast sidegraafiku koostamist. Lihtsalt kirjuta Se ja pane nool.

Näete, et kõik on lihtne! Vaatame edasi, R ja L on ühendatud järjestikku, mis tähendab, et neis voolab sama vool, kui rääkida võimsusmuutujatest - sama vool. Millisel sõlmel on sama voog? Õige vastus on 1-sõlm. 1-sõlme külge kinnitame allika, takistuse (komponent - R) ja induktiivsuse (komponent - I).

Järgmisena on meil mahtuvus ja takistus paralleelselt, mis tähendab, et neil on sama pinge või jõud. 0-sõlm sobib nagu ükski teine. Ühendame mahtuvuse (komponent C) ja takistuse (komponent R) 0-sõlmega.

Sõlmed 1 ja 0 on samuti omavahel ühendatud. Noolte suund valitakse meelevaldselt, ühenduse suund mõjutab ainult märki võrrandites.

Hankige järgmine linkide graafik:

Nüüd peame põhjuslikud seosed maha panema. Järgides nende kinnitamise järjestuse juhiseid, alustame allikast.

1. Meil on stressi (pingutuse) allikas, sellisel allikal on ainult üks põhjuslikkuse variant – väljund. Panime.
2. Siis on I komponent, vaatame, mida soovitatakse. Panime
3. Panime maha 1-sõlme jaoks. Sööma
4. 0-sõlmel peab olema üks sisend ja kõik väljundi põhjuslikud seosed. Meil on üks vaba päev. Otsime komponente C või I. Leitud. Panime
5. Näitab, mis on alles

See on kõik. Ehitatud sidegraafik. Hurraa, seltsimehed!

Ainus asi, mida teha, on kirjutada meie süsteemi kirjeldavad võrrandid. Selleks loome 3 veeruga tabeli. Esimene sisaldab kõiki süsteemi komponente, teine ​​sisaldab iga elemendi sisendmuutujat ja kolmas sisaldab sama komponendi väljundmuutujat. Oleme sisse- ja väljapääsu juba põhjusliku seose järgi määranud. Nii et probleeme ei tohiks olla.

Võrrandite kirjutamise mugavuse huvides nummerdame iga ühenduse. Võtame iga elemendi võrrandid komponentide C, R, I loendist.

Pärast tabeli koostamist defineerime olekumuutujad, selles näites on 2, p3 ja q5. Järgmisena peate kirjutama olekuvõrrandid:

See on kõik, mis mudel on valmis.

Näide 2. Tahan lihtsalt vabandada foto kvaliteedi pärast, peaasi, et lugeda oskad

Lahendame veel ühe näite mehaaniline süsteem, sama, mille lahendasime Lagrange'i meetodil. Näitan lahendust ilma kommentaarideta. Kontrollime, milline neist meetoditest on lihtsam, lihtsam.

Matipallis koostati mõlemad matimudelid samade parameetritega, mis saadi Lagrange'i meetodi ja sidegraafiku abil. Tulemus allpool: lisage sildid