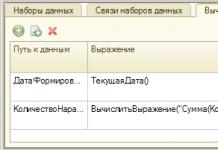
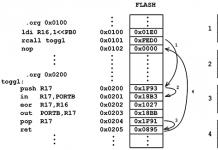
Sihtfunktsiooni ja piirangute süsteemi salvestamine erinevates lineaarses programmeerimisülesannetes ei ole sama: mõnes ülesandes on vaja leida sihtfunktsiooni miinimum ja teistes - maksimaalne; mõnel juhul sõltuvad otsitavad muutujad ühest indeksist, teistel aga kahest; mõnes ülesandes on piirangud määratud süsteemi kujul lineaarsed ebavõrdsused ja teistes – süsteemi kujul lineaarvõrrandid. Praktikas võib esineda ka probleeme, mille puhul osa piirangutest on lineaarsete võrratuste ja osa lineaarsete võrrandite kujul. Samuti ei pruugi kõik probleemid nõuda muutujate mittenegatiivsust.

Selliste erinevate lineaarsete programmeerimisprobleemide arvessevõtmine nõuab spetsiaalsete meetodite väljatöötamist nende üksikute klasside lahendamiseks. Keskendume oma tähelepanu õppimisele üldised omadused ja meetodid lineaarne programmeerimine, kirjutatud nn kanoonilises vormis.

Kui lineaarse programmeerimisülesande puhul on algpiirangute süsteem võrrandite kujul nagu

ja peate leidma lineaarse sihtfunktsiooni maksimumi

siis loetakse lineaarse programmeerimise ülesanne kanoonilisel kujul üleskirjutatuks.

Iga lineaarse programmeerimise probleemi saab hõlpsasti taandada kanooniliseks vormiks. Üldjuhul piisab selleks, et esiteks on võimalik taandada sihtfunktsiooni minimeerimise probleem selle maksimeerimise probleemiks, teiseks liikuda ebavõrdsuse piirangutelt võrdsuse piirangutele ja kolmandaks muuta neid muutujaid, mis on ei allu mittenegatiivsuse tingimusele .

Juhul, kui peate leidma funktsiooni miinimumi , saame jätkata funktsiooni maksimumi leidmisega , kuna järgmine väide on tõsi:
.

Algse probleemi ebavõrdsuse piirang, mille vorm on " ", saab muuta võrrandipiiranguks, lisades selle vasakule küljele täiendava mittenegatiivse muutuja ja vormi ebavõrdsuse piirangu ” – lahutades selle vasakust servast täiendava mittenegatiivse muutuja.

Pange tähele, et sisestatud täiendavate mittenegatiivsete muutujate arv on alati võrdne ebavõrdsete arvuga esialgses piirangute süsteemis.

Kasutusele võetud lisamuutujatel on väga spetsiifiline majanduslik tähendus. Seega, kui algse lineaarse programmeerimise probleemi piirangud peegeldavad tootmisressursside kulusid ja saadavust, siis numbriline väärtus lisamuutuja näitab vastava kasutamata ressursi hulka.

Pange tähele ka seda, et kui mõni muutuja ei allu mittenegatiivsuse tingimusele, siis tuleb see asendada kahe mittenegatiivse muutujaga Ja , olles vastu võtnud
.

Näide. Kirjutage kanoonilisel kujul järgmine lineaarse optimeerimise ülesanne: leidke funktsiooni miinimum
piirangute all

Lahendus

Selles ülesandes peate leidma sihtfunktsiooni miinimumi ja piirangute süsteem sisaldab nelja ebavõrdsust. Selle kanoonilisel kujul kirjutamiseks peate liikuma ebavõrdsuse piirangutelt võrrandipiirangutele ja ka teisendama sihtfunktsioon.

Kuna ülesande piirangute süsteemis sisalduvate võrratuste arv on võrdne neljaga, tuleb see üleminek läbi viia nelja täiendava mittenegatiivse muutuja sisseviimisega. Veelgi enam, teises ja neljandas ebavõrdsuses on märk " ", seega lisame nende vasakule küljele täiendavaid muutujaid. Esimeses ja kolmandas ebavõrdsuses on märk " “, mis tähendab, et lahutame nende vasakult küljelt täiendavad muutujad.

Teisendame ka sihtfunktsiooni, muutes kõik märgid vastupidiseks ja leiame selle maksimumi.

Seega kirjutatakse see lineaarse programmeerimise probleem järgmisel kanoonilisel kujul:

funktsiooni maksimumi leidmine

piirangute all

1. lehekülg

Ülesande kanoonilist vormi iseloomustavad järgmised kolm tunnust: 1) homogeenne piirangute süsteem võrrandisüsteemi kujul; 2) homogeensed mittenegatiivsuse tingimused, mis kehtivad kõigi probleemiga seotud muutujate kohta, ja 3) lineaarse funktsiooni maksimeerimine. Selles probleemis on kõik kolm funktsiooni rikutud.

Ülesande kanoonilist vormi iseloomustavad järgmised kolm tunnust: 1) homogeenne piirangute süsteem võrrandisüsteemi kujul; 2) homogeensed mittenegatiivsuse tingimused, mis kehtivad kõigi probleemiga seotud muutujate kohta, ja 3) lineaarse funktsiooni maksimeerimine. Selles probleemis on kõik kolm funktsiooni rikutud.

Lineaarse programmeerimise ülesande kanooniline vorm on mugav selle poolest, et teostatava piirkonna algtipu on lihtne leida.

Vaatleme lineaarse programmeerimise probleemi kanoonilist vormi ja Jordani-Gaussi elimineerimismeetodit.

Lineaarse programmeerimise probleemi kanooniline vorm on sageli mugav.

Piirangute süsteemi teisendamisel lineaarse programmeerimisülesande kanooniliseks vormiks tuleb võrratused (12) ja (13) asendada võrdustega. Selleks võetakse kasutusele täiendavad mittenegatiivsed muutujad.

Tõesta, et paarikaupa pendeldavad reaalmaatriksid taandatakse samaaegselt ülesande 1128 kanooniliseks vormiks sarnasuse teisendusega, kasutades ortogonaalset maatriksit.

Põhimõtteliselt võib (4) - (5) pidada mittelineaarse programmeerimisprobleemi kanooniliseks vormiks, kuna peatükis kirjeldatud meetodid. Tavaliselt ei ole mittelineaarsete programmeerimisülesannete puhul nõuet, et muutujad oleksid täisarvud.

Piirangute tüübid ja nende teisendamise meetodid.

Ülesande kanoonilist vormi iseloomustab piirangute süsteemi homogeensus võrrandisüsteemi kujul; eesmärgifunktsiooni maksimeerimine; kõigi probleemiga seotud muutujate mittenegatiivsuse tingimus.

Mitte ühtegi lisafunktsioone probleemide kanooniline vorm vaadeldavale arvutusskeemile ei lisa.

Vaatleme esmalt miinimumülesande teist kanoonilist vormi.

Simpleks-mete algoritmi saab jagada kaheks etapiks. Esimeses etapis leitakse muutujate kõrvaldamise teel põhilahendus. Kui see leitakse, on meil ülesande kanooniline vorm, et liikuda teise etappi. Teine samm on kontrollida, kas on olemas piiratud optimum. Kui see on olemas, siis määratakse lubatavad põhilahendused ja nende hulgast valitakse optimaalne.

Kui probleem lahendatakse kanoonilisel kujul, kasutatakse ainult osa teises lõigus toodud tehtetest. Seega realiseerub kanoonilise miinimumprobleemi puhul ainult punktis 3.4.1 kirjeldatud juhtum ning vaja on vaid sammaste tsüklilise ümberpaigutamise, veeru vertikaalse piirtsooni läbimise, konstruktsioonirikkumiste parandamise ja osa kärpimisoperatsiooni toiminguid. Sümmeetriliselt realiseeritakse kanoonilise maksimumi ülesande lahendamisel ainult punkti 3.4.2 juhtum ning stringide tsüklilise ümberpaigutamise, stringi läbimise horisontaalsest piiritsoonist, konstruktsioonirikkumiste parandamisest ja kärbimise operatsiooni muust osast. vaja. Muidu ei midagi täiendavad spetsiifikatülesande kanooniline vorm ei lisa.

Sissejuhatuse esimene lõik näitas, kuidas ühine ülesanne Lineaarse programmeerimise saab taandada ühele selle kanoonilisest vormist. Kanooniliste ülesannete puhul on järjestikuse parenduse meetodi kirjeldus formaalselt lihtsustatud, kuna pole vaja kaaluda kahte võimalust optimaalsuse tingimuste rikkumiseks ja kahte võimalust järgmise tipuni jõudmiseks, kuid see suurendab suurust alusmaatriks A [ /, J ], mis määravad peamiselt ühe shati keerukuse. Kuid paljudel juhtudel osutub eelistatavamaks meetodi rakendamine ülesande kanoonilistele vormidele ja selles osas peatume konkreetsete lineaarse programmeerimisprobleemide jaoks saadud meetodi variantidel.

Lehekülgi: 1    

Iga lineaarse programmeerimise probleemi saab taandada kanoonilisel kujul olevaks lineaarseks programmeerimisülesandeks. Selleks peate üldiselt suutma taandada maksimeerimisprobleemi minimeerimisprobleemiks; liikuda ebavõrdsuse piirangutelt võrdsuse piirangutele ja asendada muutujad, mis ei allu mittenegatiivsuse tingimusele. Teatud funktsiooni maksimeerimine võrdub sama funktsiooni minimeerimisega vastupidise märgiga ja vastupidi.

Reegel lineaarse programmeerimise probleemi vähendamiseks kanooniline vorm on järgmine:

• kui sisse algne probleem Kui soovite määrata lineaarse funktsiooni maksimumi, peaksite muutma märki ja otsima selle funktsiooni miinimumi;
• kui on piiranguid parem osa on negatiivne, siis tuleks see piir korrutada -1-ga;
• kui piirangute vahel esineb ebavõrdsusi, siis täiendavate mittenegatiivsete muutujate sisseviimisega muudetakse need võrdsusteks;
• kui mõni muutuja x j ei oma märgipiiranguid, siis asendatakse see (sihtfunktsioonis ja kõigis piirangutes) kahe uue mittenegatiivse muutuja erinevusega:
  x 3 = x 3 + - x 3 - , Kus x 3 +, x 3 - ≥ 0 .

Näide 1. Lineaarse programmeerimise probleemi taandamine kanoonilisele kujule:

min L = 2x1 + x2-x3;
2x 2 - x 3 ≤ 5;
x 1 + x 2 - x 3 ≥ -1;
2x 1 - x 2 ≤ -3;
x 1 ≤ 0; x 2 ≥ 0; x 3 ≥ 0.

Toome igasse piirangute süsteemi võrrandisse nivelleerimismuutujad x 4, x 5, x 6. Süsteem kirjutatakse võrduste kujul ning piirangute süsteemi esimeses ja kolmandas võrrandis muutujad x 4, x 6 sõlmitakse vasak pool"+" märgiga ja teises võrrandis muutuja x 5 sisestatakse "-" märgiga.

2x 2 - x 3 + x 4 = 5;
x 1 + x 2 - x 3 - x 5 = -1;
2x 1 - x 2 + x 6 = -3;
x 4 ≥ 0; x 5 ≥ 0; x 6 ≥ 0.

Kanoonilisel kujul olevad vabad liikmed peavad olema positiivsed; selleks korrutage kaks viimast võrrandit -1-ga:

2x 2 - x 3 + x 4 = 5;
-x 1 - x 2 + x 3 + x 5 = 1;
-2x 1 + x 2 - x 6 = 3.

Lineaarse programmeerimisülesannete kirjutamise kanoonilisel kujul peavad kõik piirangute süsteemis sisalduvad muutujad olema negatiivsed. Oletame, et x 1 = x 1" – x 7 , Kus x 1 "≥ 0, x 7 ≥ 0 .

Asendamine see väljend piirangute süsteemi ja sihtfunktsiooni ning kirjutades muutujad kasvavas indeksi järjekorras, saame kanoonilisel kujul esitatud lineaarse programmeerimise probleemi:

L min = 2x 1" + x 2 - x 3 - 2x 7;
2x 2 - x 3 + x 4 = 5;
-x 1" - x 2 + x 3 + x 5 + x 7 = 1;
-2x 1" + x 2 - x 6 + 2x 7 = 3;
x 1 "≥ 0; x i ≥ 0, i = 2, 3, 4, 5, 6, 7.

Kanoonilise LP-ülesande põhiplaani optimaalsustingimus. Simpleksmeetod ja selle konvergents.

Lihtne meetod on universaalne, kuna see võimaldab teil lahendada peaaegu kõik sisse kirjutatud lineaarse programmeerimise ülesanded kanooniline vorm.

Simpleksmeetodi idee plaani järjepidev täiustamine, on see, et alustades mõnest esialgsest võrdluslahendusest, järjestikku suunatud liikumineülesande etalonlahendustest optimaalseni.

Eesmärkfunktsiooni väärtus ei vähene selle liikumise käigus probleemide korral maksimaalselt.

Kuna tugilahenduste arv on lõplik, siis lõpliku arvu sammude järel saame optimaalse tugilahenduse.

Võrdluslahus on põhiline mittenegatiivne lahendus.

Simpleksmeetodi algoritm

1. Ülesande matemaatiline mudel peab olema kanooniline. Kui see on mittekanooniline, siis tuleb see viia kanoonilisele kujule.

2. Leidke esialgne võrdluslahend ja kontrollige selle optimaalsust.
Selleks täitke simpleks laud 1.
Täidame 1. sammu tabeli kõik read vastavalt piirangute süsteemi ja sihtfunktsiooni andmetele.

Võimalik järgmistel juhtudel probleemide lahendamisel maksimaalne:

1. Kui kõik koefitsiendid viimane rida simpleks tabelid Dj³ 0, siis leitud

lahendus optimaalne.

2 Kui vähemalt üks koefitsient Dj £ 0, kuid vastava muutuja puhul pole ühtegi positiivset hinnangulist seost, siis lahendus lõpetame ülesanded, kuna F(X) ® ¥ , st eesmärgifunktsioon ei ole teostatavate lahenduste osas piiratud.

Kui viimase rea vähemalt üks koefitsient on negatiivne ja vastava muutuja puhul on vähemalt üks positiivne hindav hoiak, siis tuleb liikuda teisele võrdluslahusele.

4. E kui siis on viimases reas mitu negatiivset koefitsienti aluseks olevasse muutujate veergu(BP) tutvustavad seda muutuv, mis vastab suurim sisse absoluutväärtus negatiivne koefitsient.

5. Kui vähemalt üks koefitsient Dk< 0 , Seda k - th veerg aktsepteerima saatejuhi jaoks.

6. Sest juhtiv rida aktsepteerime seda, mis vastab miinimum vabaliikmete suhe bi positiivsetele koefitsientidele juhtiv, k – see üks veerg.

7. Nimetatakse elementi, mis asub juhtivate ridade ja veeru ristumiskohas juhtiv element.

Simplekstabeli 2 täitmine :

· täitke põhiveerg nullide ja ühtedega

· kirjutage juhtrida ümber, jagades selle juhtiva elemendiga

· kui esireas on nullid, siis saab vastavad veerud liigutada järgmisse simplekstabelisse

· ülejäänud koefitsiendid leiame "ristküliku" reegli abil

Saame uue etalonlahenduse, mida kontrollime optimaalsuse huvides:

Kui kõik viimase rea koefitsiendid Dj³ 0, siis leiti lahendus maksimaalselt.

Kui ei, siis täitke 8. sammu simplekstabel ja nii edasi.

Kui sihtfunktsioon F(X) nõuab leidmist minimaalne väärtus, siis kriteerium probleemi optimaalsus on mittepositiivsed koefitsiendid D j kõigi j = 1,2,...n.

Simpleksmeetodi lähenemine. LP probleemide degeneratsioon. Iga arvutusalgoritmi kõige olulisem omadus on konvergents, st võimalus saada soovitud tulemusi selle rakendamisel (antud täpsusega) piiratud arvu etappide (iteratsioonide) jooksul.

Lihtne on näha, et r-i väärtuse valimise etapis (jaotis 2") võivad tekkida probleemid simpleksmeetodi konvergentsiga juhul, kui sama minimaalsed väärtused suhe

saavutatakse samaaegselt mitme tabeli T (q) rea puhul. Järgmisel iteratsioonil sisaldab veerg b(β(q+1)) null elementi.

: Lineaarse programmeerimise probleemid (LPP)

1. Lineaarne programmeerimine

2. Lineaarse programmeerimise ülesannete tüübid

3. Kujundid PAP-i kirjed

4. Lineaarse programmeerimise ülesannete kanooniline vorm

Lineaarne programmeerimine

Lineaarne programmeerimine on matemaatilise programmeerimise haru, mida kasutatakse ekstreemumi leidmise meetodite väljatöötamiseks lineaarsed funktsioonid mitu muutujat lineaarsega täiendavad piirangud, mis on muutujatele peale pandud.

Lahendatavate probleemide tüübi järgi jagunevad LP-meetodid universaalseteks ja spetsiaalseteks. Kasutades universaalsed meetodid Kõik lineaarse programmeerimise probleemid (LPP) on lahendatavad. Spetsiaalsed võtavad arvesse probleemmudeli tunnuseid, selle objektiivset funktsiooni ja piirangute süsteemi.

Lineaarse programmeerimise ülesannete põhijooneks on see, et sihtfunktsiooni ekstreemum asub teostatavate lahenduste piirkonna piiril.

Joonis 1 – sihtfunktsiooni ekstreemum

ZLP matemaatiline mudel on kirjutatud järgmiselt:

max (või min) Z=z(X),(1)

ODR-i saab esitada lineaarsete võrrandite või võrratuste süsteemiga.

Vektor X = (x 1, x 2, .... x p) on juhtvektor või juhtefekt.

Lubatud plaani X, milles optimaalsuse kriteerium Z=z(X) saavutab äärmusliku väärtuse, nimetatakse optimaalseks ja tähistatakse X*-ga, sihtfunktsiooni äärmist väärtust Z*=z(X*).

Lineaarse programmeerimise probleemide tüübid

Lineaarseid programmeerimismeetodeid kasutatakse tööstusettevõtetes laialdaselt tootmisprogrammi optimeerimisel, töökodade ja ajavahemike kaupa jaotamisel, seadmete sortimentide laadimisel, kaubavoogude planeerimisel, käibeplaani koostamisel jne.

Kõige tavalisem ülesannete tüüp on ülesanne optimaalne kasutamine ressursse. Laske mõnel tootmisüksusel (töökoda, ettevõte, ühistu vms), lähtudes turutingimustest, tehnilised võimalused ja olemasolevaid ressursse, suudab toota n erinevat tüüpi numbrite j all tuntud tooted.

Toodete tootmisel on ettevõte piiratud olemasolevate ressurssidega, mille kogust tähistatakse m-ga ja ressursside vektor B = (b 1, b 2, ..., b t). Tuntud on ka tehnoloogilised koefitsiendid a ij, mis näitavad i-nda ressursi kulumäära j-nda toote ühiku tootmiseks. Ühiku väljundi efektiivsus j-i tooted mida iseloomustab kasum p j .

On vaja kindlaks määrata tootmisplaan X = (x 1, x 2, ..., x p), maksimeerides etteantud ressurssidega ettevõtte kasumit.

Sihtfunktsioon näeb välja selline

piirangute all

Sageli on tootevaliku kehtestanud kõrgem organisatsioon, st selle mahud peavad jääma teatud piiridesse D j-s ja D-s j: siis seatakse järgmine piirang:

Selle aluseks on ressursside optimaalse kasutamise probleemi mudel mudelid ettevõtte iga-aastase tootmisprogrammi optimeerimiseks. Mudel sisaldab piiranguid seadmete tööajale.

Sama tähist hoides kirjutame läbi b j ja c j vastavalt müügihinna ja ühiku maksumuse jth tooted. Optimaalsuse kriteeriumidena võib võtta järgmist:

1) maksimaalne kasum

2) minimaalsed tootmiskulud

3) maksimaalne toodang väärtuses (tulu toote müügist)

Näide. Ettevõte suudab toota nelja tüüpi tooteid 1, 2, 3 ja 4. Igas mahus müük on garanteeritud. Kvartali jooksul on ettevõttes tööjõudu 100 inimvahetust, pooltooteid kaaluga 260 kg ja masinaid 370 masinavahetust. Iga tooteliigi ressursitarbimise määrad ja kasum ühiku kohta on toodud tabelis 1.

Vajalik:

a) meik matemaatiline mudelülesanne määrata tootmisplaan, mis saavutab maksimaalse kasumi;

b) lahendada probleem pakendi nõudega nii, et kolmanda toote ühikute arv oleks 3 korda suurem rohkem kogustühikud esiteks;

c) leida optimaalne sortiment lisatingimused: toota vähemalt 25 ühikut esimest toodet, mitte rohkem kui 30 ühikut kolmandat ning teist ja neljandat toodet vahekorras 1:3.

Tabel 1

Esialgsed andmed

Ülesande matemaatiline mudel:

objektiivne funktsioon:

max: Z=40x1 +50x2 +100x3 +80x4

piirangutega:

a) tööjõuressursside puhul:

2,5x1 +2,5x2 +2x3 +1,5x4? 100;

pooltoodete puhul:

4x1 +10x2 +4x3 +6x4? 260;

tööpinkide jaoks:

8x 1 +7x 2 +4x 3 +10x 4 ? 370;

mittenegatiivsuse tingimus:

b) konfiguratsiooni lisanõuet väljendab tingimus

3x1 =x3, st 3x1x3 =0;

c) esitame piirtingimused ja konfiguratsioonitingimuse järgmiselt: x 1 ? 25,

x 3?30, 3*x 2 = x 4.

Probleemid tellimuste esitamisel või vahetatavate seadmerühmade laadimisel. See on umbes o tellimuste jaotus m (i=1,..., m) erineva tootmis- ja tehnoloogiliste omadustega, kuid tellimuste täitmise mõttes omavahel asendatava ettevõtte (kauplused, masinad, esinejad) vahel. Kohustuslik on koostada tellimuste esitamise plaan, milles ülesanne oleks täidetud ja efektiivsusnäitaja saavutaks äärmusliku väärtuse.

Sõnastame ülesande matemaatiliselt. Olgu vaja toota n tüüpi tooteid, kasutades m homogeenset seadmerühma. Tootmisplaan iga tooteliigi jaoks teatud periood antud hulgaga x j (j=1,2, …n). Igat tüüpi seadmete võimsus on piiratud ja võrdne b i-ga. Tehnoloogiline maatriks A=||a ij || on teada, kus a ij on ajaühikus toodetud j-nda toote ühikute arv. i-s varustus. Maatriks C on kulumaatriks, kus c ij on toodanguga seotud kulud j-ndat ühikut tooted i-ndal seadmel. X on väljundmahu vektor.

Probleemi mudel on järgmisel kujul:

eesmärgifunktsioon – kõigi tellimuste elluviimise kulude minimeerimine

piirangutega:

a) seadme võimsuse järgi

b) tootmiseks

c) mittenegatiivsuse tingimus

Seda probleemi nimetatakse jaotus- või jaotusprobleemiks.

Kui mõne tooteliigi puhul lubatakse plaani ületada, võetakse piirangu (b) kuju

Sihtkasumiks võib võtta ka järgmist:

a) maksimaalne kasum

b) masina aja minimaalne kulu

Sest Iga mudel sisaldab lihtsustavaid eeldusi; saadud tulemuste õigeks rakendamiseks on vaja nende lihtsustuste olemust selgesti mõista, mis lõpuks võimaldab teha järelduse nende vastuvõetavuse või vastuvõetavuse kohta. Kõige olulisem lihtsustus vaadeldavates mudelites on ressursitarbimise mahtude ja tootmismahtude vahelise otseselt proportsionaalse (lineaarse) seose eeldamine, mis täpsustatakse kulunormide a ij abil. Ilmselgelt ei ole see eeldus alati täidetud. Seega muutuvad paljude ressursside (näiteks põhivara) tarbimismahud järsult – olenevalt tootmisprogrammi X muutustest. Teiste lihtsustavate eelduste hulka kuuluvad eeldused hindade j sõltumatuse kohta mahtudest x j, mis kehtivad vaid teatud piiride puhul. nende muutumisest. Samuti on oluline teada neid "haavatavaid" punkte, kuna need näitavad mudeli täiustamise põhisuundi.

PAP-i salvestusvormid

PAP-i salvestamiseks on 3 vormi:

1) funktsioonide kujul

max(või min)Z=,max(või min)Z=,

2) vektorvorm

(vektorite skalaarkorrutis)

piirangute all

A 1 x 1 +A 2 x 2 +..+A n x n = B

Kus on vektorid

C = (C 1, C 2 .. C n), X = (X 1, X 2 .. X n) ja.

3) maatriksvorm

piirangute all

kus C = (c 1, c 2,...c n),

Lineaarse programmeerimise ülesannete kanooniline vorm

Kui kõik lineaarse programmeerimise ülesande piirangud on võrrandid ja mittenegatiivsuse tingimused on kehtestatud kõikidele muutujatele x j, siis nimetatakse seda lineaarse programmeerimise probleemiks kanoonilisel kujul või kanooniliseks lineaarse programmeerimise probleemiks (CLP).

piirangute all

ZLP-lt CLLP-le üleminekuks on vaja liikuda ebavõrdsuse piirangutelt võrdsuspiirangutele ja asendada muutujad, mis ei allu mittenegatiivsuse tingimustele.

ZLP kanoonilisse vormi viimise reeglid:

1) kui piirangute parem pool on negatiivne, siis tuleb see piirang korrutada -1-ga;

2) kui piirangute vahel esineb ebavõrdsusi, siis täiendavate mittenegatiivsete muutujate sisseviimisega muudetakse need võrdsusteks;

3) kui mõnel muutujal xk pole märgipiiranguid, siis asendatakse see sihtfunktsioonis ja kõigis piirangutes kahe uue mittenegatiivse muutuja vahega: xk=x * k - xl, kus l on koondindeks, x * k>=, xl >=0.

Vaatame näidet. Toome selle kanoonilisele kujule:

Toome igasse piirangute süsteemi võrrandisse nivelleerimismuutujad x 4, x 5, x 6. Süsteem kirjutatakse võrduste kujul ning piirangute süsteemi esimeses ja kolmandas võrrandis on muutujad x 4, x 6 sisestatud vasakule küljele plussmärgiga ja teise võrrandisse x. 5 sisestatakse märgiga "-".

Kanoonilisel kujul olevad vabad liikmed peavad olema positiivsed; selleks korrutage kaks viimast võrrandit -1-ga:

Lineaarse programmeerimisülesannete kirjutamise kanoonilisel kujul peavad kõik piirangute süsteemis sisalduvad muutujad olema mittenegatiivsed. Oletame, et

Asendades selle avaldise piirangute ja sihtfunktsiooni süsteemiga ning kirjutades muutujad kasvavas indeksi järjekorras, saame kanoonilisel kujul esitatud lineaarse programmeerimise probleemi:

optimeerimise simpleksline lineaarne programmeerimine

ZLP kanooniline vorm- lineaarne programmeerimisülesanne kujul ax = b kus a on koefitsiendi maatriks, b on piiranguvektor.

Teenuse eesmärk. Veebikalkulaator on mõeldud PPP üleminekuks KZLP-le. Probleemi viimine kanoonilisele kujule tähendab, et kõik piirangud on võrdsuste kujul, lisades täiendavaid muutujaid.
Kui ühelegi muutujale x j piirangut ei kehtestata, siis asendatakse see täiendavate muutujate erinevusega, x j = x j1 - x j2, x j1 ≥ 0, x j2 ≥ 0.

Juhised. Valige muutujate arv ja ridade arv (piirangute arv). Saadud lahendus salvestatakse Wordi faili.

Muutujate arv 2 3 4 5 6 7 8 9 10
Ridade arv (piirangute arv) 2 3 4 5 6 7 8 9 10

Kuidas taandada lineaarse programmeerimise probleem kanooniliseks vormiks

ZLP matemaatilist mudelit nimetatakse põhilised, kui selles olevad piirangud on esitatud võrrandite kujul, eeldusel, et muutujad ei ole negatiivsed.

Matemaatilist mudelit nimetatakse kanooniline, kui selle piirangute süsteem on esitatud m lineaarselt sõltumatu võrrandi süsteemi kujul (süsteemi auaste r=m), eraldatakse süsteem ühiku alusel, defineeritakse vabad muutujad ja eesmärgifunktsiooni väljendatakse vabade muutujatena. Sel juhul on võrrandite parempoolsed küljed mittenegatiivsed (b i ≥ 0).

Muutujaid, mis sisalduvad ühes süsteemi võrrandis koefitsiendiga üks ja puuduvad teistes võrrandites, nimetatakse põhilised tundmatud ja kõik teised - tasuta.

Süsteemi lahendust nimetatakse põhilised, kui selles olevad vabad muutujad on võrdsed 0-ga ja sellel on vorm:
X alused = (0, 0; b 1 , …, b m), f (X alused) = c 0

Põhilahendus on süsteemi lahenduste hulga nurgapunkt, s.o. määrab mudeli lahendushulknurga tipu. Selliste lahenduste hulgas on ka see, milles sihtfunktsioon on optimaalne väärtus.

Põhilahendust nimetatakse võrdluslahenduseks, kui see on lubatav, s.t. süsteemi võrrandite (või võrratuste) kõik parempoolsed küljed on positiivsed b i ≥ 0.

Kanoonilise mudeli kompaktne vorm on:
AX = b
X ≥ 0
Z = CX(max)

Vastuvõetava lahenduse kontseptsioon, vastuvõetavate lahenduste valdkond, optimaalne lahendus lineaarse programmeerimise probleemid.
Definitsioon 1. Vektorit X, mis rahuldab ZLP piirangute süsteemi, sealhulgas mittenegatiivsuse tingimusi, kui neid on, nimetatakse ZLP lubatavaks lahenduseks.
2. definitsioon. Kõigi vastuvõetavate lahenduste kogum moodustab PLP lubatavate lahenduste piirkonna (ADA).
3. määratlus. Teostatavat lahendust, mille puhul sihtfunktsioon saavutab maksimumi (või miinimumi), nimetatakse optimaalseks lahenduseks.

Näide nr 1. Vähendage järgmine LP-ülesanne kanooniliseks vormiks: F(X) = 5x 1 + 3x 2 → max piirangute korral:
2x 1 + 3x 2 ≤20
3x 1 + x 2 ≤15
4x 1 ≤16
3x 2 ≤12
Mudel on sisse kirjutatud standardvorm. Toome sisse tasakaalu mittenegatiivsed muutujad x 3 , x 4 , x 5 , x 6 , mille lisame ebavõrdsuse piirangute vasakule küljele. Sisustusfunktsiooni lisame kõik lisamuutujad, mille koefitsiendid on võrdsed nulliga:
Esimeses tähenduse võrratuses (≤) võtame kasutusele põhimuutuja x 3 . 2. tähenduse võrratuses (≤) võtame kasutusele põhimuutuja x 4 . Kolmandas võrratuses tutvustame põhimuutujat x 5 . Neljandas võrratuses - põhimuutuja x 6. Saame mudeli kanoonilise vormi:
2x 1 + 3x 2 + 1x 3 + 0x 4 + 0x 5 + 0x 6 = 20
3x 1 + 1x 2 + 0x 3 + 1x 4 + 0x 5 + 0x 6 = 15
4x 1 + 0x 2 + 0x 3 + 0x 4 + 1x 5 + 0x 6 = 16
0x 1 + 3x 2 + 0x 3 + 0x 4 + 0x 5 + 1x 6 = 12
F(X) = 5x1 + 3x2 + 0x3 + 0x4 + 0x5 + 0x6 → max

Näide nr 2. Leidke süsteemi kaks etalonlahendust
x 1 + 2x 4 - 2x 5 = 4
x 3 + 3x 4 + x 5 = 5
x 2 + 3x 5 = 2