34. Optimaalse plaani unikaalsuse test, komplekt optimaalsed plaanid ja optimaalse plaani puudumine LP-ülesande lahendamisel simpleksmeetodil.
Probleemide lahendamisel simpleksmeetodi abil on võimalikud järgmist tüüpi optimaalsed lahendused:
1. Unikaalsus . Kui kõigi vabade vektorite hinnangud on rangelt negatiivsed, siis on saadud võrdlusplaan optimaalne ja kordumatu. (vt näide eelmises lõigus).
2. Alternatiivne optimum (optimaalsete lahenduste komplekt).
Kui vabade vektorite mittepositiivsete hinnangute hulgas on vähemalt üks null, siis on saadud võrdlusplaan optimaalne, kuid mitte ainus. Sel juhul saab edasi liikuda teiste toetusplaanide juurde (alusesse sisestatakse nullhinnangule vastavad vektorid) ja seejärel kirjutada saadud optimaalsete toetusplaanide kumera kombinatsioonina üldine optimaalne lahendus.
3. ZLP-l pole optimaalset lahendust, kuna sihtfunktsioon ei ole altpoolt piiratud . Kui simplekstabelil on positiivne skoor ja kõik elemendid sellest veerust on negatiivsed ja null, siis saab selle vektori baasi sisestada. Ühtegi alusvektorit ei saa aga baasist tuletada. Sellest järeldub, et mittereferentsplaanile üleminekul on võimalik sihtfunktsiooni edasine vähendamine.
4. ZLP-l pole optimaalset lahendust, kuna piirangute süsteem on vastuoluline. Mis ajast PPP otsus tavaline simpleksmeetod peab olema algne võrdlusplaan, siis pole lineaarvõrrandisüsteem kindlasti vastuoluline. Järelikult ei saa sellise juhtumiga kokku puutuda, kui lahendatakse tavalisel simpleksmeetodil.
5. Kui ODZ koosneb ühest punktist, siis on sellise ülesande lahendus triviaalne ja selle saab ilma simpleksmeetodit kasutamata.
35. Millistel juhtudel kasutatakse kunstliku baasi meetodit?
kunstlik.
36. M-ülesande konstrueerimine tehisliku baasi meetodil
Kui lineaarse programmeerimise probleem on käes kanooniline vorm aga mitte kõik võrrandid ei sisalda põhimuutujaid, st esialgne võrdlusplaan puudub. Sel juhul on nendes võrrandites, milles põhimuutujaid pole, lisada mõni mittenegatiivne muutuja koefitsiendiga +1. Sellist muutujat nimetatakse kunstlik.
Väga suure positiivse arvuga sihtfunktsioonile tuleb lisada tehismuutuja (kuna sihtfunktsioon on miinimumi leidmine). See number on tähistatud Ladina täht M. Seda võib pidada võrdseks +∞. Sellega seoses nimetatakse kunstlikku alusmeetodit mõnikord M-meetodiks. See transformatsioon algne probleem nimetatakse laiendatud probleemi konstrueerimiseks. Kui lahendatakse ülesannet eesmärgifunktsiooniga, tuleb sellele lisada tehismuutuja sihtfunktsioon väga suurega positiivne arv(kuna eesmärgifunktsioon on miinimumi leidmine). Seda numbrit tähistatakse ladina tähega M. Seda võib pidada võrdseks +∞. Sellega seoses nimetatakse kunstlikku alusmeetodit mõnikord M-meetodiks. Seda algse probleemi teisendust nimetatakse laiendatud probleemi konstrueerimiseks. Kui ülesanne lahendatakse maksimumi leidmiseks sihtfunktsiooniga, siis kaasatakse sihtfunktsiooni tehismuutujad koefitsiendiga –M.
Seega on laiendatud ülesandes meil võrdluskujundus (kuigi mõned baasmuutujad on kunstlikud).
Esialgne simplekstabel on konstrueeritud.
37. indeksjoone koostamine tehisliku baasmeetodil
Koostatakse esialgne simplekstabel, milles indeksirida jagatakse kaheks reaks, kuna hinnangud koosnevad kahest liikmest. IN ülemine rida hinnangu liige ilma M-ta, alumisele reale - koefitsiendid M-le. Hinnangu märk määratakse koefitsiendi M-i märgiga, sõltumata M-ta liikme väärtusest ja märgist, kuna M on väga suur positiivne arv.
Seega on baasi sisestatava vektori määramiseks vaja analüüsida alumist indeksijoont. Kui baasist tuletatakse tehisvektor, siis ei saa järgnevates simplekstabelites vastavat veergu arvutada, kui lahendust pole vaja kahekordne probleem(vaata järgmist teemat).
Pärast seda, kui kõik tehisvektorid on baasist tuletatud, alumine joon saab kõike null elementi, välja arvatud tehisvektoritele vastavad hinnangud. Need on võrdsed -1. Sellise joone võib kaalumisest eemaldada ja edasise lahenduse saab läbi viia tavalisel simpleksmeetodil, kui duaalülesande lahendust pole vaja saada (vt järgmist teemat).
38. Optimaalsuse kriteerium kunstliku baasi meetodil. Algülesande esialgse võrdlusplaani koostamise märk.
39. Algoritm kaksik-simpleksmeetodi jaoks
Dual simplex meetodi algoritm:
täitke esimene simplekstabel tavapärasel viisil, pööramata tähelepanu vabade tingimuste märkidele. Arvatakse, et sellisel probleemil peab olema esialgne ühikupõhi.
Valige juhtjoon suurima järgi absoluutväärtus vabade terminite veeru negatiivne element A0
Juhtveerg valitakse indeksirea elementide ja juhtrea negatiivsete elementide absoluutväärtuste väikseima suhte alusel.
Ülelugemine simpleks laud Jordaania täieliku välistamise reegli kohaselt
kontrollige saadud plaani vastuvõetavust. Vastuvõetava võrdlusplaani saamise märk on negatiivsete elementide puudumine veerus A0. Kui veerus A0 on negatiivseid elemente, siis minge teise punkti. Kui neid pole, jätkavad nad tekkinud probleemi lahendamist tavapärasel viisil.
märk optimaalse lahenduse leidmisest dual simplex meetod on tavapärase simpleksmeetodi optimaalsuse kriteerium.
41. Avatud ja suletud transpordimudelid. Üleminek avatud transpordimudelilt suletud mudelile.
Transpordiülesannete tüübid.
Saadaval m teadaolevate tootevarudega homogeensete toodete tarnijad ja n nende toodete tarbijad teatud vajadustega. Samuti on teada transpordi ühikukulud.
Kui tootevarude mahtude summa võrdub kõigi tarbijate vajaduste mahuga, siis seda probleemi nimetatakse suletud transpordi probleem
(st kui ∑ Ai = ∑ Bj), vastasel juhul kutsutakse välja transpordiprobleem avatud. Lahenduste jaoks transpordi probleem see peab olema suletud.
Avatud transpordiprobleemi saab teisendada suletud probleemiks järgmiselt.
Olgu ∑Ai > ∑Bj. Sel juhul on vaja kasutusele võtta fiktiivne n+1 tarbija vajaduste mahuga ∑Ai – ∑Bj Tarnijalt fiktiivse tarbijani transpordi ühikukulu eeldatakse 0-ga, kuna tegelikkuses on selline transport. ei teostata ja osa tooteid jääb tarnijatele.
Kui ∑Bj > ∑Ai . Sel juhul on vaja sisestada fiktiivne m+1 tarnija varude mahuga ∑Bj – ∑Ai . Eeldatakse, et fiktiivselt tarnijalt tarbijale transpordi ühikukulu on 0, kuna tegelikkuses sellist transporti ei teostata ja tarbijad ei saa osa tooteid kätte.
42. Transpordiprobleemi algjaotuse konstrueerimise meetodid: loodenurga meetod ja maatriksi väikseima elemendi meetod.
Loode-meetod võrdlusplaani koostamiseks. Selle meetodi järgi algab transpordiväärtuste kujunemine loodest. laua nurk, st. lahtrist x11. Selle meetodi järgi jaotatakse esmalt esimese tarnija kaubad. Pealegi rahuldab esimene tarnija esmalt esimest tarbijat nii palju kui võimalik. Seejärel, kui tarnijal on kaup alles,
Maatriksi väikseima elemendi meetod.
Meetodi olemus seisneb selles, et maksimaalne võimalik tarne paigutatakse alati lahtrisse, mis vastab maatriksi madalaimale tariifile.
Esiteks teeme märgid (näiteks ▼-märgiga) nende ridade lahtritesse, kus on täheldatud rea madalaimat hinda. Seejärel liigume tabeli veergude kaupa ringi ja teeme samad märkmed lahtritesse, mis sisaldavad veergude madalaimat hinda.
Edasine jaotamine toimub esmalt, nii palju kui võimalik, kahe märgiga lahtritesse, seejärel ühega ja seejärel tasakaalustatakse ülesanne uuesti (m + n – 1) täidisteks. Korraldame täidised liikudes läbi tabeli vasakult paremale ja ülevalt alla.
43. Transpordiprobleemide omadused
Transpordiprobleemil on mõned omadused, mida saab kajastada järgmiste teoreemidega.
1. teoreem. Suletud transpordiprobleemil on alati lahendus.
2. teoreem. Kui tootevarude ja vajaduste mahud on täisarvud, siis on ka transpordiprobleemi lahendus täisarv.
3. teoreem. suletud transpordiprobleemi piirangute süsteem on alati lineaarselt sõltuv.
Sellest teoreemist järeldub, et suletud transpordiülesande jaotuses on alati m + n – 1 põhimuutujat ja (m – 1) (n – 1) vaba aja muutujat.
44. Mandunud jaotus transpordiprobleemides, degeneratsioonist vabanemine. Läbikriipsutatud kombinatsioon.
Jaotust nimetatakse degeneratiivseks, kui rakkude arv on väiksem kui m + n – 1.
45. Transpordiprobleemi optimaalsusteoreemid.
Teoreem. Kui mõne jaotus transpordi probleem teile
tingimused on täidetud:
A). ui+vj = сij hõivatud kambrite jaoks
b) ui+vj ≤ сij, vabade rakkude jaoks,
siis on see jaotus optimaalne.
Suurusi ui nimetatakse reapotentsiaalideks ja suurusi vj veerupotentsiaalideks.
46. Potentsiaalid ja nende arvutamise meetodid.
Ridade ja veergude potentsiaalide leidmiseks kasutage optimaalsusteoreemi tingimuse a) alusel järgmist arutluskäiku.
Sellel tingimusel põhinevate võrrandite arv on võrdne m + n – 1 ning tundmatute arv ui ja vj võrdub m + n. See. muutujate arv on suurem kui võrrandite arv ja kõik võrrandid on lineaarselt sõltumatud. Sellise lineaarvõrrandisüsteemi lahendus on ebakindel, seega tuleb ühele potentsiaalile omistada mis tahes väärtus. Praktikas ui = 0. Saadakse m + n – 1 võrrandisüsteem m + n – 1 tundmatu muutujaga. Seda süsteemi saab lahendada mis tahes meetodiga. Praktikas võetakse potentsiaalide arvutamiseks arvesse hõivatud rakke, mille üks nende potentsiaalidest on teada, ja lähtudes teoreemi tingimusest a) arvutatakse ülejäänud tundmatute potentsiaalide väärtused.
47. transpordiülesannete jaotuse ja optimaalsuse kriteeriumi optimaalsuse hinnangute arvutamine.
Teoreemi seose b) põhjal saame hinnangute arvutamiseks kirjutada järgmise valemi: δ ij= ui +vj – сij. Tagamaks, et hinnanguid ei aetaks segi transpordimahtudega, on need (hinnangud) ümbritsetud ringidega.
Optimaalsuse hinnangud TZ vabades lahtrites kujutavad endast optimaalsuse kriteeriumi, mille abil kontrollitakse jaotuse optimaalsust. Kui kõigi vabade lahtrite hinded on nullist väiksemad või sellega võrdsed, on see jaotus optimaalne.
48. tarnete ümberjagamine transpordiprobleemis
Kui jaotus ei ole optimaalne, on vaja varusid ümber jagada.
Ümberjaotamiseks konstrueeritakse ümberarvutustsükkel. Lahtriks valitakse kõrgeima positiivse tulemusega lahter. See lahter on tähistatud "+" märgiga, see tähendab, et sinna tuleb kirjutada teatav tarnekogus. Kuid siis rikutakse selle veeru tasakaal, seetõttu tuleb selle veeru üks hõivatud lahtritest tähistada märgiga "-", see tähendab, et tarnemahtu tuleb sama palju vähendada. Kuid siis selle rea tasakaal muutub, seetõttu tuleb mõni selle rea hõivatud lahter märkida "+" märgiga. See protsess jätkub, kuni märk “-” asetatakse reale, kus asus algne lahter.
Iga vaba lahtri jaoks on ümberarvutustsükkel ja pealegi ainulaadne.
Võrdlusplaani optimaalsuse märk
Kui kindlat tugiplaani sisaldavas simplekstabelis on kõik f-rea elemendid (v.a vaba liige) mittenegatiivsed, siis on see tugiplaan optimaalne.. Laske tabeli f-rida sisse. 2.b 0j > (i=1, ..., n m). Selles tabelis sisalduvas võrdlusplaanis x 0 on kõigi vabade muutujate x m+j väärtused võrdsed nulliga ja f(x 0) =b 00. Kui suurendada mõnd vaba muutujat x m+ j, siis, nagu on näha võrrandist (2.5), hakkab b 0j mittenegatiivsuse tõttu f(x) väärtus vähenema. Järelikult saavutab x o funktsioon f(x) oma suurima väärtuse, mis tähendab, et x 0 on tõepoolest optimaalne võrdlusplaan.
Võimalus liikuda ühelt võrdlusplaanilt teisele
Nagu eelpool mainitud, seisneb simpleksmeetodi olemuses järgmise kriteeriumi tõestamise protsess: kui mingit võrdlusplaani sisaldava simplekstabeli f-real on vähemalt üks negatiivne element (vaba liiget arvestamata), mis vastab veerule, millel on vähemalt üks positiivne element, siis saab aluse teisendamisega liikuda teisele võrdlusplaanile, mille sihtfunktsiooni väärtus on suurem.
Tõestame seda märki. Kehtestame reeglid muutujate valimiseks selliseks algaluse B o teisenduseks võrdlusplaaniga x 0 in uus alus B 1 võrdlusplaaniga x 1, milles; funktsiooni f väärtus suureneb, st f(x i)>f(x 0). Seejärel teisendame vastavalt simplekstabelist elementide ümberarvutamise reeglile need uuele alusele, mis võimaldab leida uue võrdlusplaani komponendid.
Oletame, et tabelis. 2.1, näiteks b 0s<0, а среди элементов b is s-го столбца есть хотя бы один положительный. Полагая в равенстве (2.5) все свободные переменные х m+j кроме x m+s , равными нулю, получаем f = b oo -- b os xm+s . Из этого равенства видно, что при увеличении x m+s значение f тоже возрастает. Таким образом, при указанных в признаке условиях действительно есть возможность увеличить f(x), переходя к планам, в которых x m+s принимает положительные значения, а все остальные компоненты x m+j по-прежнему равны нулю. Покажем, что среди таких планов существует и опорный. Тем самым будет найден путь направленного преобразования базиса Б о в новый базис Б 1 . В самом деле, если переменная x m+s принимает положительное значение в некотором опорном плане, значит, она является в нем базисной компонентой (в опорном плане x о она была свободной компонентой и равнялась нулю). Поэтому прежний базис следует преобразовать за счет включения в него переменной x m+s . Но здесь предстоит решить два вопроса:
1) millised muutujatest tuleks eelmisest baasist eemaldada, et muutujale x m+s ruumi teha;
2) millise väärtuse peaks saama uus põhimuutuja x m+s uues võrdlusplaanis.
Esitatud küsimuste lahendamiseks oletame, et võrratustes (2.4) on kõik x m+j, välja arvatud x m+s, võrdsed nulliga. Siis
x i = b io -b on x m+s (i=l, ..., m)
Nendest võrdustest on selge, et x m+s suurenemisega on nende põhimuutujate x i väärtused, mille koefitsiendid b on<0, тоже будут расти, оставаясь положительными. Значит, на отрицательные коэффициенты b is можно внимания не обращать, так как они не влияют на знак базисных переменных. Иначе обстоит дело с базисными переменными, у которых b is >0. Kui x m+s suureneb, hakkavad nende muutujate väärtused kahanema ja saabub hetk, mille järel nad omandavad negatiivsed väärtused ja tingimus (2.3) ei ole enam täidetud. Seda ei saa lubada. Seetõttu uurime välja, millise piirväärtuseni x m+s saab suurendada põhimuutujate mittenegatiivsuse tingimust rikkumata. Selleks kirjutame süsteemist (2.6) välja need võrrandid, milles b on >0. Oletame, et see puudutab võrdusi arvudega i=d,…,k,…,p:
x d = b do -- b ds x m+s ,
…………………..
x k = b k0 - b ks x m+s ,
………………….
x p =b p0 - b ps x m+s .
Põhimuutujad x d, ..., x k, ..., x p jäävad mittenegatiivseteks seni, kuni x m+s rahuldab võrratuste süsteemi
b do - b ds x m+s >0, x m+s
……………… ………………
b k0 - b ks x m +s >0 või x m+s< b ko /b ks
……………… ………………
b p0 - b ps x m+s >0 x m+s< b po /b ps
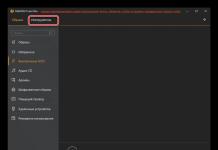
st x m+s juures Olgu väikseim murdudest b io /b vastab i = k, s.o. min ( b io /b on )= b k0 /b ks . Siis võime öelda, et seni kuni x m+s ei ületa väärtust b k0 /b ks , st x m+s 0, siis muutub muutuja x k võrdseks täpiga: x k = b k0 -- b ks b ko /b ks =0 ja seeläbi teisendatakse alus B o = (x 1 ; ...; x k ; . ..; x m ) uude baasi, milles muutuja x m+s läheb vabast rühmast põhilistesse ja muutuja x k asendab x m+s vabas rühmas. Samal ajal on kõik muud vabad muutujad endiselt võrdsed nulliga ja ülejäänud põhimuutujad on endiselt positiivsed. Järelikult on põhiplaanil x 1 uues baasis B 1 = (x 1 ; ...; x m+s ; ...; x m ) m positiivset komponenti ja m-n nulli. Kavas x 1 võivad mõned põhimuutujad omandada nullväärtused kahel juhul: 1) kui plaanis x 0 on nulliga võrdsed põhimuutujad; 2) kui väikseim murdudest b io /b vastab kahele või enamale arvule i. Meie puhul vastab see ainult i = k. Alusesse kaasatav muutuja määratakse f-stringi negatiivse elemendiga. Võrdusest f =b oo - b os x m+s on selge, et kui b 0s<0 и фиксированном x m+s >0, sõltub f(x) väärtus koefitsiendi b 0s absoluutväärtusest: mida suurem |b 0s |, seda suurema väärtuse f(x) uues baasis saab. Aga sellest võrdsusest selgub ka, et uue baasmuutuja poolt võetud väärtusest sõltub ka sihtfunktsiooni väärtus uues baasis x m+s. Valime baasi sisestatud muutuja, keskendudes ainult f-rea negatiivsetele elementidele. Seega, kui f-real on mitu negatiivset elementi, siis sisestame baasi suurima absoluutväärtusega negatiivsele elemendile vastava muutuja x m+j. Aluses sisalduva muutuja koefitsientide veergu nimetatakse lahendamiseks. Seega, valides f-rea negatiivse elemendi alusel baasi sisestatud muutuja (või valides lahendava veeru), tagame funktsiooni f suurenemise. Baasist välja jäetava muutuja määramine on veidi keerulisem. Selleks koostavad nad vabade liikmete suhted lahendava veeru positiivsete elementide vahel (sellisi seoseid nimetatakse simpleksiks) ja leiavad nende hulgast väikseima, mis määrab välistatud muutujat sisaldava rea (lahutav). Alusest välja jäetud muutuja valik (või lahutusrea valik) minimaalse simpleksseotuse järgi tagab baaskomponentide positiivsuse uues võrdlusplaanis. Seega oleme tõestanud, et märgis määratud tingimustel on tõepoolest võimalik suure sihtfunktsiooni f(x) väärtusega ühelt võrdlusplaanilt teisele liikuda. Pange tähele, et uue baasmuutuja x m+s väärtust teame juba uues võrdlusplaanis: see on võrdne b ko /b ks . Mis puudutab uue võrdlusplaani ülejäänud põhimuutujate arvväärtusi ja vastavat f(x) väärtust, siis need on leitavad alles pärast muudetud põhimuutujate süsteemi x 1 ;..., x m+s ; ...,x m väljendatakse vabade muutujate x m+1,…,x k,…, x n modifitseeritud süsteemi kaudu. Selleks seadistame; reeglid, mille järgi probleemi tingimused muudetakse ühelt aluselt teisele. Selles võrrandis olevat koefitsienti b ks = 0 x m+s nimetatakse lahutuselemendiks. Võrdsuses (2.7) väljendub uus põhimuutuja x m+s vabade muutujatena, mille hulgas nüüd asub endine põhimuutuja x k. Seega vahetusid muutujad x m+s ja x k rollid. Samamoodi väljendame ülejäänud põhimuutujaid uue vabade muutujate komplekti kaudu. Selleks asendame ülejäänud võrdsustest väärtuse x m+s (tähistame f väärtusega x 0, siis võetakse võrdsus süsteemi i = 0 juures) Süsteemi viimist uuele alusele nimetatakse simpleksteisenduseks. Kui vaadelda simpleksteisendust kui formaalset algebralist tehtet, siis võib märgata, et selle toimingu tulemusena jaotuvad rollid ümber kahe muutuja vahel, mis kuuluvad teatud lineaarfunktsioonide süsteemi: üks muutuja muutub sõltuvast sõltumatuks ja teine. , vastupidi, sõltumatust ülalpeetavaks . Seda operatsiooni tuntakse algebras kui Jordani eliminatsioonietappi. Lihtne meetod. Algoritm. Võrdlusplaani optimaalsuse märk. ZLP geomeetrilisest tõlgendusest on selge, et funktsiooni maksimum või miinimum saavutatakse kumera hulktahuka - ODP - piirangute süsteemi nurgapunktis. Seetõttu põhineb simpleksmeetod ideel kaaluda ja optimaalsust testida ainult nurgapunkte - hulktahuka tippe, mitte kogu selle punktide lõpmatut komplekti. Riis. Simpleksmeetodi idee geomeetriline tõlgendus kahe (joonis a) ja kolme (joonis b) muutuja puhul. Lihtne on kumer hulknurk n-mõõtmelises ruumis n+1 tipuga, mis ei asu samas hüpertasandis (hüpertasand jagab ruumi 2 poolruumiks). Lihtne meetod on arvutusprotseduur, mis põhineb lahenduse järjestikuse täiustamise põhimõttel. Sel juhul liigume ühest baaspunktist teise. Sihtfunktsiooni väärtus paraneb alati. Põhilahendus– see on üks ODR-is leitud vastuvõetavaid lahendusi. Nimetatakse muutujaid, mille jaoks on lahendatud lineaarvõrrandisüsteem põhilised. Seejärel kutsutakse kõiki teisi muutujaid tasuta. On tõestatud, et kui optimaalne lahendus on olemas, siis leitakse see lõpliku arvu sammudega, välja arvatud silmuste puhul. Simpleksmeetodi algoritm: 1. Koostage ülesande matemaatiline mudel. Võrdlusplaani optimaalsuse märk Kui lahendame ülesande max väärtusega, peavad kõik hinnangud olema mittenegatiivsed. Kui lahendame ülesande min jaoks, peavad kõik hinnangud olema mittepositiivsed. Kui võrdlusplaan ei ole optimaalne, peate üle minema parema võrdlusplaani juurde. Selleks valime halvima hinnangu. See vastab eraldusvõime veerule. Pärast seda peate leidma lubamisrea. Θ (simpleksseoste veerg) ei joonista negatiivsete ja nullväärtustega ridadele. Kõigist θ-dest valime väikseima, seda tehakse alati olenemata sellest, kas algülesanne on min või max. Lahendusrida näitab alati, milline element tuleb aluselt eemaldada, ja lahutusveerul on alati näha, milline element tuleb alusele sisestada. PPP tabelivaade. Simplex - tabelid. LIHTNE MEETOD ZLP LAHENDAMISEKS 3.1. Simpleksmeetodi üldised omadused ja põhietapid Simpleksmeetodi rajajad on nõukogude matemaatik L.V. Kantorovich ja Ameerika matemaatik J. Dantzig. Simpleksmeetodi abil saate lahendada mis tahes probleemi või avastada selle lahendamatuse. Paljusid eriülesannete klasse saab lahendada teiste meetoditega, mis on nende klasside jaoks tõhusamad. Simpleksmeetodi eeliseks on aga selle mitmekülgsus. Peaaegu kõigi arvutite jaoks on välja töötatud standardprogrammid probleemide lahendamiseks simpleksmeetodil. Kirjeldame simpleksmeetodi üldist ideed. Usume, et ZLP on kirjutatud kanoonilises vormis ja eesmärgifunktsiooni tuleb minimeerida. Nagu me juba teame, tuleks optimaalset plaani otsida ZLP põhiplaanide hulgast. Simpleksmeetod ei läbi kõiki võrdlusplaane (mis oleks nende tohutu hulga tõttu sageli võimatu), vaid alates mõnest esialgsest võrdlusplaanist liigub see järjestikku teiste võrdlusplaanide juurde eesmärgifunktsiooni vähenemisega. Simpleksmeetod lakkab töötamast, kui leitakse optimaalne võrdlusplaan või tuvastatakse probleemi lahendamatus. Probleemi lahendamisel simpleksmeetodi abil saab eristada järgmisi etappe: 1) ZLP viimine kanoonilisse vormi; 2) lineaarvõrrandisüsteemi taandamine Jordani vormile mittenegatiivsete parempoolsete külgedega, kontrollides samal ajal elukestva õppe programmi lahendamatust lineaarsete piirangute süsteemi vastuolu tõttu; 3) optimaalsuse võrdlusplaani uurimine; 4) ZLP uurimine eesmärgifunktsiooni ODD altpoolt piiramatuse tõttu otsustamatuse osas; 5) üleminek uuele, “paremale” referentsplaanile. Kirjete vähendamiseks ja korrastamiseks ZLP lahendamisel simpleksmeetodil kasutatakse nn simplekstabeleid. Simplekstabeli kasutamiseks tuleb ZLP teisendada tabelivormiks. Seda tehakse nii. Olgu ZLP kirjutatud kanoonilises vormis (2.3-2.5). ZLP taandamiseks tabelikujuliseks tuleks süsteem (2.4) esmalt taandada Jordani kujule, millel on mittenegatiivsed parempoolsed küljed. Oletame, et sellel Jordani kujul on vorm (2.6). Avaldame (2.6) põhimuutujad vabade kujul: Asendades sihtfunktsiooni (2.3) põhimuutujate asemel nende avaldised vabade muutujate kaudu valemite (3.1) järgi, jätame seega põhimuutujad sihtfunktsioonist välja. Eesmärgifunktsioon on järgmisel kujul: Tabelina kirjutatakse eesmärgifunktsioon järgmiselt: Kus Märgime PPP tabelivormi järgmisi tunnuseid: a) lineaarvõrrandisüsteem taandatakse Jordani kujule, millel on mittenegatiivsed parempoolsed küljed; b) põhimuutujad jäetakse sihtfunktsioonist välja ja see kirjutatakse kujul (3.3). Liigume nüüd edasi simplekstabeli kirjelduse juurde. Olgu ZLP kirjutatud tabeli kujul: Siis näeb valmis simplekstabel välja selline. Tabel 3.1. PPL põhiplaan:
..., nimetatakse sellele simplekstabelile vastavaks võrdlusplaaniks. Nagu valemist (3.2) näha, on selle võrdlusplaani sihtfunktsiooni väärtus võrdne γ 0. Vaatame näidet. Vähendage järgmine ZLP tabelivormiks ja täitke simplekstabel: Esiteks tuleks ZLP viia kanoonilisse vormi. Selleks kasutatakse funktsiooni f
tuleb asendada -f-ga: Võrrandisüsteem tuleb kirjutada Jordaania kujul mittenegatiivsete parempoolsete külgedega. Üldist tehnikat, mille abil see saavutatakse, arutatakse hiljem (jaotis 3.7). Meie näites on selline Jordani vorm juba baasmuutujatega ja . Jätame sihtfunktsioonist välja põhimuutujad - f. Selleks väljendame neid vabade väljenditena ja asendame need väljendid sihtfunktsiooniga. ZLP tabelivaade on järgmine: Täidame simplekstabeli (kirjete lühendamiseks kannab esimene veerg pealkirjaga “B”, viimane veerg “Q”). Tabel 3.2. Sellele simplekstabelile vastav võrdlusplaan on järgmisel kujul: Funktsiooni - f väärtus selle võrdlusplaaniga on -20. Olgu siis täidetud simplekstabel. Sõnastagem võrdlusplaani optimaalsustingimus. Kui simplekstabeli alumine rida sisaldab kõiki numbreid, välja arvatud võib-olla parempoolseim, mittepositiivne, siis on sellele tabelile vastav võrdlusplaan optimaalne. Lihtsuse huvides põhjendame selle väite paikapidavust näitega. Laske valminud simplekstabel välja näha selline: Tabel 3.3. Simplekstabelile vastava võrdlusplaani sihtfunktsiooni väärtus on 6. Kirjutame eesmärgifunktsiooni tabeli kujul: 3.4. Elukestva õppe programmi otsustamatuse tingimus, mis tuleneb sihtfunktsiooni ODD altpoolt piiramatusest. Kui ZLP jaoks on täidetud simplekstabel, siis ülesande ODD on mittetühi, seega kuulub simplekstabelile vastav võrdlusplaan ODD-sse. Siiski võib ZLP olla lahendamatu, kuna sihtfunktsiooni ODD on altpoolt piiritlemata. Otsustamatuse tingimus on sõnastatud järgmiselt. Kui simplekstabel sisaldab vähemalt ühte veergu, välja arvatud parempoolseim, mille alumises reas on positiivne arv ja veeru kõigis teistes ridades mittepositiivsed numbrid, siis on ZLP lahendamatu, kuna ODD sihtfunktsioon on altpoolt piiramatu. Selle õigustamiseks toome taas näite. Tabel 3.4. Alumise rea veerg sisaldab positiivset arvu ja ülejäänud read sisaldavad mittepositiivseid numbreid. Tõestame ZLP otsustamatust. Kirjutame välja simplekstabelile vastava Jordani vormi ja liigutame , sisaldavad terminid paremale poole. Saame Olgu a suvaline positiivne arv. Ilmselt on ZLP-l järgmine teostatav lahendus:. Arvutame selle teostatava lahenduse jaoks välja sihtfunktsiooni väärtuse. Tabelist 3.4 on meil: 3.5. Üleminek uuele võrdlusplaanile. Oletame, et optimaalsuse ja otsustamatuse tingimused ei ole täidetud. Seejärel liigub simpleksmeetod uude võrdlusplaani. See üleminek saavutatakse ühe põhimuutuja eemaldamisega baasist ja ühe vaba muutuja sisestamisega baasi. Sel juhul peavad olema täidetud kaks järgmist tingimust: 1) uus alus peab ikka lubatav olema, s.t. vastava Jordani vormi parempoolsed küljed peavad siiski olema mittenegatiivsed; 2) uue võrdlusplaani puhul ei tohiks sihtfunktsiooni väärtus ületada selle väärtust eelmise võrdlusplaaniga. Alusse sisestatud muutujat sisaldavat simplekstabeli veergu kutsutakse üldine veerg. Nimetatakse rida, mis sisaldab baasist tuletatud muutujat üldine joon. Nimetatakse elementi, mis asub üldrea ja üldveeru ristumiskohas üldine element. Üldelemendi valimise reegel. Üldveeruks valitakse kõik simplekstabeli veerud, välja arvatud parempoolseim ja mille alumises reas on positiivne arv. Siis võetakse arvesse ainult neid simplekstabeli ridu peale madalaima, millel on positiivsed arvud ristumiskohas üldveeruga. Iga selle rea jaoks arvutatakse vaba liikme ja üldveerus oleva elemendi suhe. Üldise rida valitakse, mille puhul see suhe on minimaalne. Üldise rea ja üldise veeru ristumiskohas olev element on üldelement. Illustreerime seda reeglit näitega. Tabel 3.5. Üldveerguks saate valida veeru või veeru. Valime (enamasti valitakse veerg, mille allosas on suurim positiivne arv). Nüüd hakkame valima üldjoont. Selleks kaaluge kahte rida - ja . Teeme suhted 4:2 ja 8:3. Suhe 4:2 on väiksema väärtusega, seega valime esimese rea üldiseks. Seetõttu on üldelement 2 - see seisab veeru ja rea ristumiskohas. Peale üldelemendi valimist tuleb liikuda uuele võrdlusplaanile, milles muutuja muutub põhiliseks ja muutuja x 1 vabaks. Uuel Jordani vormil peab koefitsient for olema võrdne 1-ga. Seetõttu jagatakse tabeli 3.5 esimene rida 2-ga. Seejärel korrutatakse saadud esimene rida arvuga (-3) ja liidetakse teisele reale. ,
teisest võrrandist välja jätta. Samamoodi, kasutades Jordani protseduuri, jätame selle välja kolmandast võrrandist ja sihtfunktsioonist (viimane eeldab ZLP tabelivormi). Selle tulemusena saame järgmise tabeli. Tabel 3.6 Pange tähele, et veerus Q esimesed kolm rida sisaldavad mittenegatiivseid numbreid, st. uus alus on endiselt kehtiv. See ei ole juhuslik fakt: see on alati nii, kui järgitakse rangelt üldjoone valimise reeglit. Edasi on sihtfunktsiooni väärtus uue võrdlusplaaniga võrdne -2, vanaga 12. Võrdlusplaani “täiustamine” tagab üldveeru valiku reegli. Kuigi me ei tõesta neid fakte rangelt, tuleb meeles pidada, et need esinevad alati. Vaadates tabelit H.6, näeme, et ei ole täidetud ei võrdlusplaani optimaalsuse ega ZLP lahendamatuse tingimus. See tähendab, et peame uuesti valima üldise elemendi ja liikuma edasi uuele simplekstabelile. Lugeja saab seda ise teha. 3.6. Tabeliline simpleksalgoritm. Olgu siis täidetud simplekstabel. Eelnevat kokku võttes saame järgmise algoritmi LLP lahendamiseks simpleksmeetodil. 1. Kui simplekstabeli alumises reas on kõik arvud, välja arvatud ehk parempoolseim, mittepositiivsed, siis on simplekstabelile vastav võrdlusplaan optimaalne ja algoritm peatub. Vastasel juhul minge punkti 2 juurde. 2. Kui simplekstabel sisaldab muud veergu kui parempoolseim, mille alumises reas on positiivne arv ja kõigis teistes ridades mittepositiivsed arvud, siis on elukestva õppe programm lahendamatu, kuna tabelis on ODD altpoolt piiramatus. eesmärgifunktsiooni ja algoritm peatub. Vastasel juhul minge punkti 3 juurde. 3. Valige mõni muu veerg peale parempoolseima, mille alumisel real on positiivne arv – nimetagem seda üldiseks. Seejärel vaatleme neid simplekstabeli ridu, mis ei ole alumised ja millel on üldises veerus positiivsed arvud. Iga selle rea jaoks arvutame vaba liikme suhte üldise veerus oleva elemendiga. Rida, mille puhul see seos on minimaalne, on üldine rida. Üldelemendiks on element, mis asub üldise veeru ja üldrea ristumiskohas. Mine punkti 4 juurde. 4. Loome uue simplekstabeli, milles: 1) üldreal olev muutuja tuletatakse alusest; baasi sisestatakse muutuja üldises veerus; 2) üldjoon jaguneb üldelemendiks; 3) Jordani protseduuri kasutades muudetakse kõik üldveerus olevad numbrid, välja arvatud 1, mis on üldreal, võrdseks nulliga. Mine punkti 1 juurde. Näide I Lahendage simpleksmeetodil Ülesanne on kirjutatud kanoonilises vormis, peate selle viima tabelivormi. Võrrandisüsteem on kirjutatud Jordani kujul mittenegatiivsete parempoolsete külgedega (põhimuutujad ja ). Eesmärkfunktsioon on vaja taandada tabelikujuliseks. Selleks väljendame põhimuutujaid vabadena x 3 = 10 - 2x 1 - x 2 x 4 = 8 - x 1 - 2x 2 ja asendage see sihtfunktsiooniga Tabelivormi saamiseks kirjutame funktsiooni järgmiselt: Nüüd on meil ZLP tabelivaade: Täidame esimese simplekstabeli Tabel 3.7 Tabelis 3.7 ei ole optimaalsuse ja otsustamatuse tingimused täidetud. Valime üldiseks veeruks , mille alumisel real on positiivne arv. Seejärel, võrreldes suhteid 10:3 ja 8:1, valime esimese rea üldiseks. Tabelis on üldelement 2. Toimides vastavalt tabeli simpleksalgoritmi punktile 4, liigume edasi tabeli 3.8 juurde. Tabel 3.8 Optimaalsuse ja otsustamatuse tingimused ei ole täidetud. Valige tabelis 3.8 üldelement ja liikuge järgmise tabeli juurde Tabel 3.9 Tabel 3.9 vastab optimaalsuse tingimusele. Vastus: optimaalne plaan Sihtfunktsiooni minimaalne väärtus f min = - 24. Näide 2. Lahendage simpleksmeetodi abil: Kõigepealt tuleb ZLP viia kanoonilisse vormi Nüüd viime ZLP tabelina. Näeme, et võrrandisüsteem on kirjutatud Jordani kujul mittenegatiivsete parempoolsete külgedega (ja z-põhimuutujatega). Eesmärkfunktsioon sisaldab aga baasmuutujat. Meil on: Seetõttu on ZLP tabelivaade järgmine: Täitke simplekstabel (tabel 3.10). Tabel 3.10 Pärast üldelemendi valimist minge tabeli 3.11 juurde PPP tabelivaade. Simplex - tabelid. LIHTNE MEETOD ZLP LAHENDAMISEKS 3.1. Simpleksmeetodi üldised omadused ja põhietapid Simpleksmeetodi rajajad on nõukogude matemaatik L.V. Kantorovich ja Ameerika matemaatik J. Dantzig. Simpleksmeetodi abil saate lahendada mis tahes probleemi või avastada selle lahendamatuse. Paljusid eriülesannete klasse saab lahendada teiste meetoditega, mis on nende klasside jaoks tõhusamad. Simpleksmeetodi eeliseks on aga selle mitmekülgsus. Peaaegu kõigi arvutite jaoks on välja töötatud standardprogrammid probleemide lahendamiseks simpleksmeetodil. Kirjeldame simpleksmeetodi üldist ideed. Usume, et ZLP on kirjutatud kanoonilises vormis ja eesmärgifunktsiooni tuleb minimeerida. Nagu me juba teame, tuleks optimaalset plaani otsida ZLP põhiplaanide hulgast. Simpleksmeetod ei läbi kõiki võrdlusplaane (mis oleks nende tohutu hulga tõttu sageli võimatu), vaid alates mõnest esialgsest võrdlusplaanist liigub see järjestikku teiste võrdlusplaanide juurde eesmärgifunktsiooni vähenemisega. Simpleksmeetod lakkab töötamast, kui leitakse optimaalne võrdlusplaan või tuvastatakse probleemi lahendamatus. Probleemi lahendamisel simpleksmeetodi abil saab eristada järgmisi etappe: 1) ZLP viimine kanoonilisse vormi; 2) lineaarvõrrandisüsteemi taandamine Jordani vormile mittenegatiivsete parempoolsete külgedega, kontrollides samal ajal elukestva õppe programmi lahendamatust lineaarsete piirangute süsteemi vastuolu tõttu; 3) optimaalsuse võrdlusplaani uurimine; 4) ZLP uurimine eesmärgifunktsiooni ODD altpoolt piiramatuse tõttu otsustamatuse osas; 5) üleminek uuele, “paremale” referentsplaanile. Kirjete vähendamiseks ja korrastamiseks ZLP lahendamisel simpleksmeetodil kasutatakse nn simplekstabeleid. Simplekstabeli kasutamiseks tuleb ZLP teisendada tabelivormiks. Seda tehakse nii. Olgu ZLP kirjutatud kanoonilises vormis (2.3-2.5). ZLP taandamiseks tabelikujuliseks tuleks süsteem (2.4) esmalt taandada Jordani kujule, millel on mittenegatiivsed parempoolsed küljed. Oletame, et sellel Jordani kujul on vorm (2.6). Avaldame (2.6) põhimuutujad vabade kujul: Asendades sihtfunktsiooni (2.3) põhimuutujate asemel nende avaldised vabade muutujate kaudu valemite (3.1) järgi, jätame seega põhimuutujad sihtfunktsioonist välja. Eesmärgifunktsioon on järgmisel kujul: Tabelina kirjutatakse eesmärgifunktsioon järgmiselt: Kus Märgime PPP tabelivormi järgmisi tunnuseid: a) lineaarvõrrandisüsteem taandatakse Jordani kujule, millel on mittenegatiivsed parempoolsed küljed; b) põhimuutujad jäetakse sihtfunktsioonist välja ja see kirjutatakse kujul (3.3). Liigume nüüd edasi simplekstabeli kirjelduse juurde. Olgu ZLP kirjutatud tabeli kujul: Siis näeb valmis simplekstabel välja selline.

![]() .
. (3.4)
(3.4)Alus Muutujad Tasuta liikmed
...
x k
...
...
...
...
...
.
.
.
. .
. .
...
. .
. .
. .
...
. .
. . .
...
...
f
...
....



B
K
-5
-7
-2
-f -4
-20
B
K
-1
-1
f
-5
-3
-1
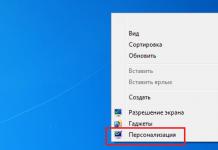
![]() , kus. Kuna ZLP mis tahes lubatava lahenduse korral võtavad muutujad ainult mittenegatiivseid väärtusi, on sihtfunktsiooni viimasest sisestusest selge, et selle väärtus ODD mis tahes punktis ei ole väiksem kui 6. Järelikult on muutuja minimaalne väärtus. Objektifunktsioon ODD-l on 6 ja see saavutatakse simplekstabelile vastava võrdlusplaaniga .
, kus. Kuna ZLP mis tahes lubatava lahenduse korral võtavad muutujad ainult mittenegatiivseid väärtusi, on sihtfunktsiooni viimasest sisestusest selge, et selle väärtus ODD mis tahes punktis ei ole väiksem kui 6. Järelikult on muutuja minimaalne väärtus. Objektifunktsioon ODD-l on 6 ja see saavutatakse simplekstabelile vastava võrdlusplaaniga .B
K
-2
-3
-1
f
-1

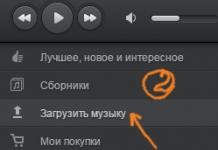
![]() . Määratud teostatava lahendusega f = 4 - 2a. Sellest näeme, et piisavalt suure a väärtuse korral võib sihtfunktsiooni väärtus muutuda nii väikeseks, kui soovitakse. Teisisõnu, sihifunktsioon ei ole ODD-l altpoolt piiratud. Seetõttu on ZLP otsustamatu.
. Määratud teostatava lahendusega f = 4 - 2a. Sellest näeme, et piisavalt suure a väärtuse korral võib sihtfunktsiooni väärtus muutuda nii väikeseks, kui soovitakse. Teisisõnu, sihifunktsioon ei ole ODD-l altpoolt piiratud. Seetõttu on ZLP otsustamatu.B
K
2
-1
-2
F
B
K
f
-2

![]()

B
K
F
B
K
F
-5
-22
B
K
F
-24



B
z K
-1
z
-2
g
-1
![]() .
. (3.4)
(3.4)