Pöördmaatriksi saamine. Maatriksalgebra – pöördmaatriks. Pöördmaatrikslahendus

Sest pöördmaatriks Arvu pöördväärtusega on asjakohane analoogia. Iga numbri jaoks a, ei võrdu nulliga, on selline arv b et töö a Ja b võrdub ühega: ab= 1. Number b nimetatakse arvu pöördväärtuseks b. Näiteks arvu 7 puhul on pöördväärtus 1/7, kuna 7*1/7=1.

Pöördmaatriks , mis tuleb antud ruutmaatriksi jaoks leida A, nimetatakse sellist maatriksit

mille korrutis maatriksid A paremal on identiteedimaatriks, st.
. (1)

Identiteetmaatriks on diagonaalmaatriks, milles kõik diagonaalelemendid on võrdsed ühega.

Pöördmaatriksi leidmine- probleem, mida sageli lahendatakse kahel viisil:

algebralise liitmise meetod, mis nõuab determinantide leidmist ja maatriksite transponeerimist;
Gaussi meetod tundmatute kõrvaldamiseks, mis nõuab maatriksite elementaarsete teisenduste läbiviimist (ridade lisamine, ridade korrutamine sama arvuga jne).

Eriti uudishimulike jaoks on ka teisi meetodeid, näiteks lineaarsete teisenduste meetod. Selles õppetükis analüüsime kolme nimetatud meetodit ja algoritmi nende meetodite abil pöördmaatriksi leidmiseks.

Teoreem.Iga mitteainsuse (mitte-degenereerunud, mitteainsuse) ruutmaatriksi jaoks võib leida pöördmaatriksi ja ainult ühe. Spetsiaalse (degenereerunud, ainsuse) ruutmaatriksi jaoks pöördmaatriksit ei eksisteeri.

Ruutmaatriksit nimetatakse pole eriline(või mitte-mandunud, mitteainsuses), kui selle determinant ei ole null, ja eriline(või degenereerunud, ainsus), kui selle determinant on null.

Maatriksi pöördväärtuse saab leida ainult ruutmaatriksi puhul. Loomulikult on ka pöördmaatriks ruut ja antud maatriksiga samas järjekorras. Maatriksit, mille jaoks võib leida pöördmaatriksi, nimetatakse inverteeritavaks maatriksiks.

Pöördmaatriksi leidmine Gaussi tundmatu elimineerimismeetodi abil

Esimene samm maatriksi pöördväärtuse leidmiseks Gaussi elimineerimismeetodi abil on maatriksi määramine A samas järjekorras identiteedimaatriks, eraldades need vertikaalse ribaga. Saame kahekordse maatriksi. Korrutame selle maatriksi mõlemad pooled arvuga , siis saame

Algoritm pöördmaatriksi leidmiseks Gaussi tundmatu elimineerimismeetodi abil

1. Maatriksile A määrata samas järjekorras identiteedimaatriks.

2. Teisenda saadud duaalmaatriks nii, et selle vasakul küljel saad ühikmaatriksi, siis paremal pool identiteedimaatriksi asemele automaatselt pöördmaatriksi. Maatriks A vasakul pool on teisendatud identiteedimaatriksiks.

2. Kui maatriksiteisenduse protsessis A identiteedimaatriksis on igas reas või veerus ainult nullid, siis on maatriksi determinant võrdne nulliga ja järelikult ka maatriks A on ainsuses ja sellel ei ole pöördmaatriksit. Sel juhul pöördmaatriksi edasine määramine peatub.

Näide 2. Maatriksi jaoks

leida pöördmaatriks.

ja me teisendame selle nii, et vasakul pool saame identiteedimaatriksi. Alustame ümberkujundamist.

Korrutage vasaku ja parema maatriksi esimene rida (-3) ja lisage see teisele reale ning seejärel korrutage esimene rida (-4) ja lisage see kolmandale reale, siis saame

Tagamaks, et järgnevates teisendustes ei esineks murdarvusid, loome esmalt duaalmaatriksi vasakpoolses teises reas ühiku. Selleks korrutage teine rida 2-ga ja lahutage sellest kolmas rida, siis saame

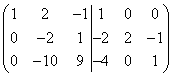Liidame esimese rea teisega ja seejärel korrutame teise rea (-9)-ga ja lisame selle kolmanda reaga. Siis saame

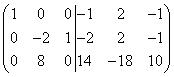Seejärel jagage kolmas rida 8-ga

Korrutage kolmas rida 2-ga ja lisage see teisele reale. Selgub:

Vahetame teise ja kolmanda rea, siis lõpuks saame:

Näeme, et vasakul pool on meil identiteedimaatriks, seega paremal pool on pöördmaatriks. Seega:

Arvutuste õigsust saate kontrollida, korrutades algse maatriksi leitud pöördmaatriksiga:

Tulemuseks peaks olema pöördmaatriks.

Interneti-kalkulaator pöördmaatriksi leidmiseks .

Näide 3. Maatriksi jaoks

leida pöördmaatriks.

Lahendus. Kahekordse maatriksi koostamine

ja me muudame selle.

Korrutame esimese rea 3-ga ja teise 2-ga ja lahutame teisest ning seejärel korrutame esimese rea 5-ga ja kolmanda 2-ga ja lahutame kolmandast reast, siis saame

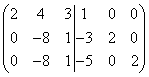Korrutame esimese rea 2-ga ja lisame selle teisele ning seejärel lahutame kolmandast reast teise, siis saame

Näeme, et vasakpoolsel kolmandal real on kõik elemendid võrdsed nulliga. Seetõttu on maatriks ainsus ja sellel pole pöördmaatriksit. Lõpetame pöördmaritzi edasise leidmise.

Lahendust saate kontrollida kasutades

ALGEBRAALISED TÄIENDUSED JA ALAALANE

Olgu meil kolmandat järku determinant: .

Alaealine, mis vastab sellele elemendile a ij kolmandat järku determinandiks nimetatakse teist järku determinandi, mis saadakse antud determinandist, kustutades rea ja veeru, mille ristumiskohas antud element seisab, s.t. i-th rida ja j veerus. Minorid, mis vastavad antud elemendile a ij me tähistame M ij.

Näiteks, alaealine M 12, mis vastab elemendile a 12, saab olema määraja , mis saadakse sellest determinandist 1. rea ja 2. veeru kustutamisel.

Seega näitab kolmandat järku determinanti defineeriv valem, et see determinant on võrdne 1. rea elementide korrutiste summaga neile vastavate alaealiste kaupa; sel juhul elemendile vastav moll a 12, võetakse “–” märgiga, st. me võime seda kirjutada

(1)

Samamoodi võib alaealiste definitsioonid kasutusele võtta teist ja kõrgemat järku determinantide jaoks.

Tutvustame veel üht kontseptsiooni.

Algebraline komplement element a ij determinanti nimetatakse selle minoorseks M ij, korrutatuna (–1) i+j .

Elemendi algebraline täiend a ij tähistatud A ij.

Definitsioonist saame, et seost elemendi algebralise täiendi ja selle molli vahel väljendab võrdsus A ij= (–1) i+j Mij.

Näiteks,

Näide. Determinant on antud. Otsi A 13, A 21, A 32.

On lihtne näha, et kasutades elementide algebralisi liitmisi, saab valemi (1) kirjutada järgmiselt:

Sarnaselt selle valemiga saate determinandi laiendada mis tahes rea või veeru elementideks.

Näiteks determinandi lagunemise 2. rea elementideks võib saada järgmiselt. Determinandi omaduse 2 järgi on meil:

Laiendame saadud determinandi 1. rea elementideks.

(2)

Siit sest teist järku determinandid valemis (2) on elementide alaealised 21, 22, 23. Seega, st. saime determinandi lagunemise 2. rea elementideks.

Samamoodi saame determinandi laiendamise kolmanda rea elementideks. Kasutades determinantide omadust 1 (transpositsiooni kohta), saame näidata, et sarnased laiendused kehtivad ka veergude elementide kohal laiendamisel.

Seega kehtib järgmine teoreem.

Teoreem (determinandi laiendamise kohta üle antud rea või veeru). Determinant on võrdne selle mis tahes rea (või veeru) elementide ja nende algebraliste täiendite korrutistega.

Kõik eelnev kehtib ka mis tahes kõrgema järgu determinantide kohta.

Näited.

PÖÖRDMAATRIKS

Pöördmaatriksi mõiste võetakse kasutusele ainult selleks ruutmaatriksid.

Kui A on siis ruutmaatriks tagurpidi selle jaoks on maatriks maatriks, tähistatud A-1 ja tingimuse rahuldamine. (See määratlus võetakse kasutusele analoogia põhjal arvude korrutamisega)

Paljudes omadustes sarnane pöördväärtusega.

Entsüklopeediline YouTube

1 / 5

✪ Pöördmaatriks (2 võimalust leida)

✪ Kuidas leida maatriksi pöördväärtust - bezbotvy

✪ Pöördmaatriks nr 1

✪ Võrrandisüsteemi lahendamine pöördmaatriksmeetodil - bezbotvy

✪ Pöördmaatriks

Subtiitrid

Pöördmaatriksi omadused

det A − 1 = 1 det A (\displaystyle \det A^(-1)=(\frac (1)(\det A))), Kus det (\displaystyle \\det) tähistab determinanti.
(A B) − 1 = B − 1 A − 1 (\displaystyle \ (AB)^(-1)=B^(-1)A^(-1)) kahe ruudu pööratava maatriksi jaoks A (\displaystyle A) Ja B (\displaystyle B).
(A T) − 1 = (A − 1) T (\displaystyle \ (A^(T))^(-1)=(A^(-1))^(T)), Kus (. . .) T (\displaystyle (...)^(T)) tähistab transponeeritud maatriksit.
(k A) − 1 = k − 1 A − 1 (\displaystyle \ (kA)^(-1)=k^(-1)A^(-1)) mis tahes koefitsiendi jaoks k ≠ 0 (\displaystyle k\not =0).
E − 1 = E (\displaystyle \E^(-1)=E).
Kui on vaja lahendada lineaarvõrrandisüsteem, (b on nullist erinev vektor), kus x (\displaystyle x) on soovitud vektor ja kui A − 1 (\displaystyle A^(-1)) on siis olemas x = A − 1 b (\displaystyle x=A^(-1)b). Vastasel juhul on lahendusruumi mõõde suurem kui null või pole lahendusi üldse.

Meetodid pöördmaatriksi leidmiseks

Kui maatriks on pööratav, saate pöördmaatriksi leidmiseks kasutada ühte järgmistest meetoditest:

Täpsed (otsesed) meetodid

Gaussi-Jordaania meetod

Võtame kaks maatriksit: the A ja vallaline E. Esitame maatriksi A identiteedimaatriksile Gaussi-Jordani meetodil, rakendades teisendusi mööda ridu (teisendusi saab rakendada ka veergude kaupa, kuid mitte segada). Pärast iga toimingu rakendamist esimesele maatriksile rakendage sama toiming ka teisele. Kui esimese maatriksi taandamine ühikuvormiks on lõpule viidud, võrdub teine maatriksiga A-1.

Gaussi meetodi kasutamisel korrutatakse esimene maatriks vasakul ühe elementaarmaatriksiga Λ i (\displaystyle \Lambda _(i))(transvektsioon- või diagonaalmaatriks, mille maatriks on põhidiagonaalis, välja arvatud üks asukoht):

Λ 1 ⋅ ⋯ ⋅ Λ n ⋅ A = Λ A = E ⇒ Λ = A − 1 (\displaystyle \Lambda _(1)\cdot \dots \cdot \Lambda _(n)\cdot A=\Lambda A=E \Paremnool \Lambda =A^(-1)). Λ m = [ 1 … 0 − a 1 m / a m m 0 … 0 … 0 … 1 - a m - 1 m / a m m 0 … 0 0 … 0 1 / a m m 0 … 0 0 … 0 - a m + 1 m / a m m 1 … 0 … 0 … 0 − a n m / a m m 0 … 1 ] (\displaystyle \Lambda _(m)=(\begin(bmatrix)1&\dots &0&-a_(1m)/a_(mm)&0&\ dots &0\\ &&&\punktid &&&\\0&\punktid &1&-a_(m-1m)/a_(mm)&0&\punktid &0\\0&\punktid &0&1/a_(mm)&0&\punktid &0\\0&\punktid &0&-a_( m+1m)/a_(mm)&1&\punktid &0\\&&&\punktid &&&\\0&\punktid &0&-a_(nm)/a_(mm)&0&\punktid &1\end(bmaatriks))).

Teine maatriks pärast kõigi toimingute rakendamist on võrdne Λ (\displaystyle \Lambda), see tähendab, et see on soovitud. Algoritmi keerukus - O (n 3) (\displaystyle O(n^(3))).

Algebralise komplementmaatriksi kasutamine

Maatriksi pöördvõrdeline maatriks A (\displaystyle A), saab esitada kujul

A − 1 = adj (A) det (A) (\displaystyle (A)^(-1)=(((\mbox(adj))(A)) \over (\det(A))))

Kus adj (A) (\displaystyle (\mbox(adj))(A))- adjointmaatriks;

Algoritmi keerukus sõltub determinandi O det arvutamise algoritmi keerukusest ja on võrdne O(n²)·O det.

LU/LUP lagunemise kasutamine

Maatriksvõrrand A X = I n (\displaystyle AX=I_(n)) pöördmaatriksi jaoks X (\displaystyle X) võib pidada kollektsiooniks n (\displaystyle n) vormi süsteemid A x = b (\displaystyle Ax=b). Tähistame i (\displaystyle i) maatriksi veerus X (\displaystyle X) läbi X i (\displaystyle X_(i)); Siis A X i = e i (\displaystyle AX_(i)=e_(i)), i = 1 , … , n (\displaystyle i=1,\ldots ,n), sest i (\displaystyle i) maatriksi veerus I n (\displaystyle I_(n)) on ühikvektor e i (\displaystyle e_(i)). teisisõnu, pöördmaatriksi leidmine taandub n võrrandi lahendamisele sama maatriksi ja erinevate parempoolsete külgedega. Pärast LUP-i lagunemist (O(n³) aeg) võtab iga n võrrandi lahendamine O(n²) aega, seega nõuab see töö osa ka O(n³) aega.

Kui maatriks A ei ole ainsus, saab selle jaoks arvutada LUP-i dekompositsiooni P A = L U (\displaystyle PA=LU). Lase P A = B (\displaystyle PA=B), B – 1 = D (\displaystyle B^(-1)=D). Seejärel saame pöördmaatriksi omadustest kirjutada: D = U − 1 L − 1 (\displaystyle D=U^(-1)L^(-1)). Kui korrutada see võrdus U ja L-ga, saate vormi kaks võrdsust U D = L − 1 (\displaystyle UD=L^(-1)) Ja D L = U − 1 (\displaystyle DL=U^(-1)). Esimene neist võrdsustest on n² lineaarvõrrandi süsteem n (n + 1) 2 (\displaystyle (\frac (n(n+1))(2))) millest on teada paremad küljed (kolmnurkmaatriksite omadustest). Teine esindab ka n² lineaarvõrrandi süsteemi n (n − 1) 2 (\displaystyle (\frac (n(n-1))(2))) millest on teada paremad küljed (ka kolmnurkmaatriksite omadustest). Koos esindavad nad n² võrdsuste süsteemi. Neid võrdusi kasutades saame rekursiivselt määrata maatriksi D kõik n² elemendid. Siis võrrandist (PA) −1 = A −1 P −1 = B −1 = D. saame võrdsuse A − 1 = D P (\displaystyle A^(-1)=DP).

LU dekompositsiooni kasutamise korral pole maatriksi D veergude permutatsiooni vaja, kuid lahendus võib lahkneda isegi siis, kui maatriks A on mitteainsuses.

Algoritmi keerukus on O(n³).

Iteratiivsed meetodid

Schultzi meetodid

( Ψ k = E − A U k , U k + 1 = U k ∑ i = 0 n Ψ k i (\displaystyle (\begin(cases)\Psi _(k)=E-AU_(k),),\\U_() k+1)=U_(k)\summa _(i=0)^(n)\Psi _(k)^(i)\lõpp(juhtumid)))

Vea hinnang

Esialgse lähenemise valimine

Siin käsitletud iteratiivsete maatriksi inversiooniprotsesside esialgse lähenduse valimise probleem ei võimalda käsitleda neid iseseisvate universaalsete meetoditena, mis konkureerivad näiteks maatriksite LU dekomponeerimisel põhinevate otseste inversioonimeetoditega. Valimiseks on mõned soovitused U 0 (\displaystyle U_(0)), tagades tingimuse täitmise ρ (Ψ 0) < 1 {\displaystyle \rho (\Psi _{0})<1} (maatriksi spektraalraadius on väiksem kui ühtsus), mis on vajalik ja piisav protsessi konvergentsi jaoks. Kuid sel juhul on esiteks vaja ülalt teada pöördmaatriksi A või maatriksi spektri hinnangut. A A T (\displaystyle AA^(T))(nimelt kui A on sümmeetriline positiivne kindel maatriks ja ρ (A) ≤ β (\displaystyle \rho (A)\leq \beta ), siis võite võtta U 0 = α E (\displaystyle U_(0)=(\alpha )E), Kus; kui A on suvaline mitteainsuse maatriks ja ρ (A A T) ≤ β (\displaystyle \rho (AA^(T))\leq \beta ), siis nad usuvad U 0 = α A T (\displaystyle U_(0)=(\alpha )A^(T)), kus ka α ∈ (0 , 2 β) (\displaystyle \alpha \in \left(0,(\frac (2)(\beta ))\right)); Muidugi saate olukorda lihtsustada ja seda ära kasutada ρ (A A T) ≤ k A A T k (\displaystyle \rho (AA^(T))\leq (\mathcal (k))AA^(T)(\mathcal (k))), pane U 0 = A T ‖ A A T ‖ (\displaystyle U_(0)=(\frac (A^(T))(\|AA^(T)\|)))). Teiseks, sellisel viisil esialgse maatriksi täpsustamisel pole garantiid, et ‖ Ψ 0 ‖ (\displaystyle \|\Psi _(0)\|) saab olema väike (võib-olla isegi osutub ‖ Ψ 0 ‖ > 1 (\displaystyle \|\Psi _(0)\|>1)) ja konvergentsimäära kõrget järjekorda ei avaldata kohe.

Näited

Maatriks 2x2

Avaldist ei saa sõeluda (süntaksiviga): (\displaystyle \mathbf(A)^(-1) = \begin(bmatrix) a & b \\ c & d \\ \end(bmatrix)^(-1) = \ frac (1)(\det(\mathbf(A))) \begin& \!\!-b \\ -c & \,a \\ \end(bmatrix) = \frac(1)(ad - bc) \ algus (bmaatriks) \,\,\,d & \!\!-b\\ -c & \,a \\ \end(bmaatriks).)

2x2 maatriksi ümberpööramine on võimalik ainult tingimusel, et a d − b c = det A ≠ 0 (\displaystyle ad-bc=\det A\neq 0).

Olgu n-ndat järku ruutmaatriks

Maatriks A -1 nimetatakse pöördmaatriks maatriksi A suhtes, kui A*A -1 = E, kus E on n-ndat järku identsusmaatriks.

Identiteedi maatriks- selline ruutmaatriks, milles kõik elemendid piki põhidiagonaali, mis lähevad ülemisest vasakust nurgast paremasse alumisse nurka, on ühed ja ülejäänud on nullid, näiteks:

pöördmaatriks võib eksisteerida ainult ruutmaatriksite jaoks need. nende maatriksite jaoks, milles ridade ja veergude arv langeb kokku.

Pöördmaatriksi olemasolutingimuse teoreem

Selleks, et maatriksil oleks pöördmaatriks, on vajalik ja piisav, et see ei oleks ainsus.

Maatriksit A = (A1, A2,...A n) nimetatakse mitte-mandunud, kui veeruvektorid on lineaarselt sõltumatud. Maatriksi lineaarselt sõltumatute veeruvektorite arvu nimetatakse maatriksi auastmeks. Seetõttu võime öelda, et pöördmaatriksi eksisteerimiseks on vajalik ja piisav, et maatriksi aste oleks võrdne selle mõõtmega, s.t. r = n.

Algoritm pöördmaatriksi leidmiseks

Kirjutage tabelisse maatriks A võrrandisüsteemide lahendamiseks Gaussi meetodil ja määrake sellele paremale (võrrandite parempoolsete külgede asemele) maatriks E.
Kasutades Jordani teisendusi, taandada maatriks A maatriksiks, mis koosneb ühikveergudest; sel juhul on vaja maatriksi E samaaegselt teisendada.
Vajadusel korralda viimase tabeli read (võrrandid) ümber nii, et algse tabeli maatriksi A alla saad identiteedimaatriksi E.
Kirjutage üles pöördmaatriks A -1, mis asub viimases tabelis algse tabeli maatriksi E all.

Näide 1

Maatriksi A jaoks leidke pöördmaatriks A -1

Lahendus: Kirjutame maatriksi A ja omistame paremale identiteedimaatriksi E. Jordani teisendusi kasutades taandame maatriksi A identiteedimaatriksiks E. Arvutused on toodud tabelis 31.1.

Kontrollime arvutuste õigsust, korrutades algmaatriksi A ja pöördmaatriksi A -1.

Maatriksi korrutamise tulemusena saadi identsusmaatriks. Seetõttu tehti arvutused õigesti.

Vastus:

Maatriksvõrrandite lahendamine

Maatriksvõrrandid võivad välja näha järgmised:

AX = B, HA = B, AXB = C,

kus A, B, C on määratud maatriksid, X on soovitud maatriks.

Maatriksvõrrandid lahendatakse võrrandi korrutamisel pöördmaatriksitega.

Näiteks maatriksi leidmiseks võrrandist peate selle võrrandi korrutama vasakul olevaga.

Seetõttu tuleb võrrandile lahenduse leidmiseks leida pöördmaatriks ja korrutada see võrrandi paremal küljel oleva maatriksiga.

Teised võrrandid lahendatakse sarnaselt.

Näide 2

Lahendage võrrand AX = B, kui

Lahendus: Kuna pöördmaatriks on võrdne (vt näide 1)

Maatriksmeetod majandusanalüüsis

Koos teistega kasutatakse ka neid maatriksmeetodid. Need meetodid põhinevad lineaar- ja vektormaatriksalgebral. Selliseid meetodeid kasutatakse keerukate ja mitmemõõtmeliste majandusnähtuste analüüsimiseks. Kõige sagedamini kasutatakse neid meetodeid siis, kui on vaja anda võrdlev hinnang organisatsioonide ja nende struktuuriüksuste toimimisele.

Maatriksanalüüsi meetodite rakendamise protsessis võib eristada mitmeid etappe.

Esimesel etapil moodustatakse majandusnäitajate süsteem ja selle põhjal koostatakse lähteandmete maatriks, milleks on tabel, mille üksikutel ridadel on süsteeminumbrid näidatud (i = 1,2,....,n), ja vertikaalsetes veergudes - indikaatorite numbrid (j = 1,2,....,m).

Teises etapis Iga vertikaalse veeru jaoks tuvastatakse suurim saadaolevatest indikaatori väärtustest, mida peetakse üheks.

Pärast seda jagatakse kõik selles veerus kajastatud summad suurima väärtusega ja moodustatakse standardiseeritud koefitsientide maatriks.

Kolmandas etapis kõik maatriksi komponendid on ruudus. Kui neil on erinev tähendus, määratakse igale maatriksinäitajale teatud kaalukoefitsient k. Viimase väärtuse määrab ekspertarvamus.

Viimasel, neljas etapp leitud reitinguväärtused R j on rühmitatud nende suurenemise või vähenemise järjekorras.

Väljatoodud maatriksmeetodeid tuleks kasutada näiteks erinevate investeerimisprojektide võrdleval analüüsil, aga ka organisatsioonide tegevuse muude majandusnäitajate hindamisel.

1. Leidke algmaatriksi determinant. Kui , siis on maatriks ainsus ja pöördmaatriksit pole. Kui, siis on olemas mittedegenereerunud ja pöördmaatriks.

2. Leidke maatriks, millesse on transponeeritud.

3. Leidke elementide algebralised täiendid ja koostage nendest adjointmaatriks.

4. Koostame valemi abil pöördmaatriksi.

5. Kontrollime pöördmaatriksi arvutuse õigsust, lähtudes selle definitsioonist:.

Näide. Leidke selle maatriksi pöördväärtus: .

Lahendus.

1) Maatriksdeterminant

2) Leidke maatriksi elementide algebralised täiendid ja koostage nendest adjointmaatriks:

3) Arvutage pöördmaatriks:

4) Kontrollige:

№4Maatriksi auaste. Maatriksiridade lineaarne sõltumatus

Mitmete matemaatiliste ja rakenduslike ülesannete lahendamiseks ja uurimiseks on oluline maatriksjärgu mõiste.

Suurusmaatriksis saate mis tahes read ja veerud kustutades eraldada ruudukujulised alammaatriksid, mis on järjekorras, kus. Selliste alammaatriksite determinante nimetatakse maatriksjärjestuse alaealised .

Näiteks maatriksitest saate 1., 2. ja 3. järgu alammaatrikse.

Definitsioon. Maatriksi auaste on selle maatriksi nullist erineva alaea kõrgeim järk. Nimetus: või.

Definitsioonist järeldub:

1) Maatriksi aste ei ületa selle mõõtmetest väiksemat, s.o.

2) siis ja ainult siis, kui maatriksi kõik elemendid on võrdsed nulliga, s.o.

3) N-ndat järku ruutmaatriksi jaoks siis ja ainult siis, kui maatriks ei ole ainsuses.

Kuna maatriksi kõigi võimalike minooride otsene loetlemine, alustades suurimast suurusest, on keeruline (aeganõudev), siis kasutatakse elementaarmaatriksiteisendusi, mis säilitavad maatriksi auastme.

Elementaarmaatriksi teisendused:

1) Nullrea (veeru) kõrvalejätmine.

2) Rea (veeru) kõigi elementide korrutamine arvuga.

3) Maatriksi ridade (veergude) järjekorra muutmine.

4) Ühe rea (veeru) igale elemendile teise rea (veeru) vastavate elementide lisamine, korrutatuna suvalise arvuga.

5) Maatriksi transpositsioon.

Definitsioon. Maatriksist elementaarteisenduste abil saadud maatriksit nimetatakse ekvivalentseks ja tähistatakse A IN.

Teoreem. Maatriksi auaste elementaarmaatriksiteisenduste käigus ei muutu.

Elementaarsete teisenduste abil saate maatriksi taandada nn astmevormiks, kui selle järgu arvutamine pole keeruline.

Maatriksit nimetatakse ešeloniks, kui sellel on vorm:

Ilmselt on astmemaatriksi auaste võrdne nullist erineva ridade arvuga, kuna on väike järjekord, mis ei ole võrdne nulliga:

Näide. Määrake maatriksi auaste elementaarteisenduste abil.

Maatriksi järjestus võrdub nullist erinevate ridade arvuga, s.o. .

№5Maatriksiridade lineaarne sõltumatus

Antud suurusmaatriks

Tähistame maatriksi ridu järgmiselt:

Neid kahte rida nimetatakse võrdne , kui nende vastavad elemendid on võrdsed. .

Tutvustame stringi arvuga korrutamise ja stringide liitmise tehteid elemendi haaval:

Definitsioon. Rida nimetatakse maatriksi ridade lineaarseks kombinatsiooniks, kui see on võrdne nende ridade korrutistega suvaliste reaalarvudega (mis tahes arvudega):

Definitsioon. Maatriksi ridu nimetatakse lineaarselt sõltuv , kui on numbreid, mis ei ole samaaegselt võrdsed nulliga, nii et maatriksiridade lineaarne kombinatsioon on võrdne nullreaga:

Kus. (1.1)

Maatriksi ridade lineaarne sõltuvus tähendab, et vähemalt 1 rida maatriksist on ülejäänud lineaarne kombinatsioon.

Definitsioon. Kui ridade lineaarne kombinatsioon (1.1) on võrdne nulliga siis ja ainult siis, kui kõik koefitsiendid on , siis nimetatakse ridu lineaarselt sõltumatu .

Maatriksjärgu teoreem . Maatriksi järjestus on võrdne selle lineaarselt sõltumatute ridade või veergude maksimaalse arvuga, mille kaudu kõik teised read (veerud) on lineaarselt väljendatud.

Teoreem mängib olulist rolli maatriksanalüüsis, eriti lineaarvõrrandisüsteemide uurimisel.

№6Tundmatutega lineaarvõrrandisüsteemi lahendamine

Lineaarvõrrandisüsteeme kasutatakse majandusteaduses laialdaselt.

Muutujatega lineaarsete võrrandite süsteem on järgmine: