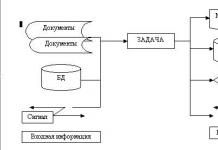
Topik ini akan merangkumi operasi seperti menambah dan menolak matriks, mendarab matriks dengan nombor, mendarab matriks dengan matriks, dan memindahkan matriks. Semua simbol yang digunakan pada halaman ini diambil dari topik sebelumnya.
Penambahan dan penolakan matriks.
Jumlah $A+B$ matriks $A_(m\times n)=(a_(ij))$ dan $B_(m\times n)=(b_(ij))$ dipanggil matriks $C_(m \times n) =(c_(ij))$, dengan $c_(ij)=a_(ij)+b_(ij)$ untuk semua $i=\overline(1,m)$ dan $j=\overline( 1,n) $.
Definisi yang sama diperkenalkan untuk perbezaan matriks:
Perbezaan antara matriks $A-B$ $A_(m\times n)=(a_(ij))$ dan $B_(m\times n)=(b_(ij))$ ialah matriks $C_(m\times n)=( c_(ij))$, dengan $c_(ij)=a_(ij)-b_(ij)$ untuk semua $i=\overline(1,m)$ dan $j=\overline(1, n)$.
Penjelasan untuk entri $i=\overline(1,m)$: show\hide
Notasi "$i=\overline(1,m)$" bermakna parameter $i$ berbeza dari 1 hingga m. Sebagai contoh, notasi $i=\overline(1,5)$ menunjukkan bahawa parameter $i$ mengambil nilai 1, 2, 3, 4, 5.
Perlu diingat bahawa operasi tambah dan tolak ditakrifkan hanya untuk matriks yang sama saiz. Secara umum, penambahan dan penolakan matriks adalah operasi yang jelas secara intuitif, kerana ia pada asasnya bermaksud penjumlahan atau penolakan unsur-unsur yang sepadan.
Contoh No. 1
Tiga matriks diberikan:
$$ A=\left(\begin(array) (ccc) -1 & -2 & 1 \\ 5 & 9 & -8 \end(array) \right)\;\; B=\left(\begin(array) (ccc) 10 & -25 & 98 \\ 3 & 0 & -14 \end(array) \right); \;\; F=\left(\begin(array) (cc) 1 & 0 \\ -5 & 4 \end(array) \right). $$
Adakah mungkin untuk mencari matriks $A+F$? Cari matriks $C$ dan $D$ jika $C=A+B$ dan $D=A-B$.
Matriks $A$ mengandungi 2 baris dan 3 lajur (dengan kata lain, saiz matriks $A$ ialah $2\kali 3$), dan matriks $F$ mengandungi 2 baris dan 2 lajur. Saiz matriks $A$ dan $F$ tidak sepadan, jadi kami tidak boleh menambahnya, i.e. operasi $A+F$ tidak ditakrifkan untuk matriks ini.
Saiz matriks $A$ dan $B$ adalah sama, i.e. Data matriks mengandungi bilangan baris dan lajur yang sama, jadi operasi penambahan boleh digunakan untuknya.
$$ C=A+B=\left(\begin(array) (ccc) -1 & -2 & 1 \\ 5 & 9 & -8 \end(array) \right)+ \left(\begin(array ) (ccc) 10 & -25 & 98 \\ 3 & 0 & -14 \end(array) \right)=\\= \left(\begin(array) (ccc) -1+10 & -2+( -25) & 1+98 \\ 5+3 & 9+0 & -8+(-14) \end(array) \right)= \left(\begin(array) (ccc) 9 & -27 & 99 \\ 8 & 9 & -22 \end(array) \kanan) $$
Mari cari matriks $D=A-B$:
$$ D=A-B=\left(\begin(array) (ccc) -1 & -2 & 1 \\ 5 & 9 & -8 \end(array) \right)- \left(\begin(array) ( ccc) 10 & -25 & 98 \\ 3 & 0 & -14 \end(array) \right)=\\= \left(\begin(array) (ccc) -1-10 & -2-(-25 ) & 1-98 \\ 5-3 & 9-0 & -8-(-14) \end(array) \right)= \left(\begin(array) (ccc) -11 & 23 & -97 \ \2 & 9 & 6 \end(array) \kanan) $$
Jawab: $C=\left(\begin(array) (ccc) 9 & -27 & 99 \\ 8 & 9 & -22 \end(array) \right)$, $D=\left(\begin(array) (ccc) -11 & 23 & -97 \\ 2 & 9 & 6 \end(array) \right)$.
Mendarab matriks dengan nombor.
Hasil darab matriks $A_(m\times n)=(a_(ij))$ dengan nombor $\alpha$ ialah matriks $B_(m\times n)=(b_(ij))$, dengan $ b_(ij)= \alpha\cdot a_(ij)$ untuk semua $i=\overline(1,m)$ dan $j=\overline(1,n)$.
Ringkasnya, mendarab matriks dengan nombor tertentu bermakna mendarab setiap elemen matriks tertentu dengan nombor itu.
Contoh No. 2
Matriks diberikan: $ A=\left(\begin(array) (ccc) -1 & -2 & 7 \\ 4 & 9 & 0 \end(array) \right)$. Cari matriks $3\cdot A$, $-5\cdot A$ dan $-A$.
$$ 3\cdot A=3\cdot \left(\begin(array) (ccc) -1 & -2 & 7 \\ 4 & 9 & 0 \end(array) \right) =\left(\begin( tatasusunan) (ccc) 3\cdot(-1) & 3\cdot(-2) & 3\cdot 7 \\ 3\cdot 4 & 3\cdot 9 & 3\cdot 0 \end(array) \right)= \left(\begin(array) (ccc) -3 & -6 & 21 \\ 12& 27 & 0 \end(array) \right).\\ -5\cdot A=-5\cdot \left(\begin (tatasusunan) (ccc) -1 & -2 & 7 \\ 4 & 9 & 0 \end(array) \kanan) =\left(\begin(array) (ccc) -5\cdot(-1) & - 5\cdot(-2) & -5\cdot 7 \\ -5\cdot 4 & -5\cdot 9 & -5\cdot 0 \end(array) \right)= \left(\begin(array) ( ccc) 5 & 10 & -35 \\ -20 & -45 & 0 \end(array) \kanan). $$
Tatatanda $-A$ ialah tatatanda singkatan untuk $-1\cdot A$. Iaitu, untuk mencari $-A$ anda perlu mendarab semua elemen matriks $A$ dengan (-1). Pada asasnya, ini bermakna bahawa tanda semua elemen matriks $A$ akan berubah kepada sebaliknya:
$$ -A=-1\cdot A=-1\cdot \left(\begin(array) (ccc) -1 & -2 & 7 \\ 4 & 9 & 0 \end(array) \right)= \ left(\begin(array) (ccc) 1 & 2 & -7 \\ -4 & -9 & 0 \end(array) \right) $$
Jawab: $3\cdot A=\left(\begin(array) (ccc) -3 & -6 & 21 \\ 12& 27 & 0 \end(array) \right);\; -5\cdot A=\left(\begin(array) (ccc) 5 & 10 & -35 \\ -20 & -45 & 0 \end(array) \right);\; -A=\left(\begin(array) (ccc) 1 & 2 & -7 \\ -4 & -9 & 0 \end(array) \right)$.
Hasil darab dua matriks.
Takrif operasi ini adalah rumit dan, pada pandangan pertama, tidak jelas. Oleh itu, saya akan nyatakan dahulu definisi umum, dan kemudian kami akan melihat secara terperinci tentang maksudnya dan cara mengendalikannya.
Hasil darab matriks $A_(m\kali n)=(a_(ij))$ dengan matriks $B_(n\kali k)=(b_(ij))$ ialah matriks $C_(m\kali k )=(c_( ij))$, yang mana setiap elemen $c_(ij)$ adalah sama dengan hasil tambah hasil yang sepadan unsur-unsur ke-i baris matriks $A$ ke elemen lajur ke-j matriks $B$: $$c_(ij)=\sum\limits_(p=1)^(n)a_(ip)b_(pj), \ ;\; i=\overline(1,m), j=\overline(1,n).$$
Mari kita lihat pendaraban matriks langkah demi langkah menggunakan contoh. Walau bagaimanapun, anda harus segera ambil perhatian bahawa tidak semua matriks boleh didarab. Jika kita ingin mendarab matriks $A$ dengan matriks $B$, maka pertama sekali kita perlu memastikan bahawa bilangan lajur matriks $A$ adalah sama dengan bilangan baris matriks $B$ (matriks sedemikian sering dipanggil dipersetujui). Contohnya, matriks $A_(5\kali 4)$ (matriks mengandungi 5 baris dan 4 lajur) tidak boleh didarab dengan matriks $F_(9\kali 8)$ (9 baris dan 8 lajur), kerana nombor lajur matriks $A $ tidak sama dengan bilangan baris matriks $F$, i.e. $4\neq 9$. Tetapi anda boleh mendarab matriks $A_(5\darab 4)$ dengan matriks $B_(4\darab 9)$, kerana bilangan lajur matriks $A$ adalah sama dengan bilangan baris matriks $ B$. Dalam kes ini, hasil pendaraban matriks $A_(5\kali 4)$ dan $B_(4\kali 9)$ akan menjadi matriks $C_(5\kali 9)$, yang mengandungi 5 baris dan 9 lajur:
Contoh No. 3
Matriks yang diberi: $ A=\left(\begin(array) (cccc) -1 & 2 & -3 & 0 \\ 5 & 4 & -2 & 1 \\ -8 & 11 & -10 & -5 \end (tatasusunan) \kanan)$ dan $ B=\left(\begin(array) (cc) -9 & 3 \\ 6 & 20 \\ 7 & 0 \\ 12 & -4 \end(array) \right) $. Cari matriks $C=A\cdot B$.
Mula-mula, mari segera tentukan saiz matriks $C$. Oleh kerana matriks $A$ mempunyai saiz $3\kali 4$, dan matriks $B$ mempunyai saiz $4\kali 2$, maka saiz matriks $C$ ialah: $3\kali 2$:

Jadi, hasil daripada hasil darab matriks $A$ dan $B$, kita harus memperoleh matriks $C$, yang terdiri daripada tiga baris dan dua lajur: $ C=\left(\begin(array) (cc) c_ (11) & c_( 12) \\ c_(21) & c_(22) \\ c_(31) & c_(32) \end(array) \kanan)$. Jika sebutan unsur menimbulkan persoalan, maka anda boleh melihat topik sebelumnya: "Matriks. Jenis matriks. Istilah asas", pada permulaannya penetapan unsur matriks dijelaskan. Matlamat kami: untuk mencari nilai semua elemen matriks $C$.
Mari kita mulakan dengan elemen $c_(11)$. Untuk mendapatkan unsur $c_(11)$, anda perlu mencari jumlah hasil darab unsur baris pertama matriks $A$ dan lajur pertama matriks $B$:

Untuk mencari elemen $c_(11)$ itu sendiri, anda perlu mendarabkan elemen baris pertama matriks $A$ dengan elemen sepadan lajur pertama matriks $B$, i.e. unsur pertama kepada yang pertama, yang kedua kepada yang kedua, yang ketiga kepada yang ketiga, yang keempat kepada yang keempat. Kami meringkaskan keputusan yang diperoleh:
$$ c_(11)=-1\cdot (-9)+2\cdot 6+(-3)\cdot 7 + 0\cdot 12=0. $$
Mari kita teruskan penyelesaian dan cari $c_(12)$. Untuk melakukan ini, anda perlu mendarabkan elemen baris pertama matriks $A$ dan lajur kedua matriks $B$:

Sama seperti yang sebelumnya, kami mempunyai:
$$ c_(12)=-1\cdot 3+2\cdot 20+(-3)\cdot 0 + 0\cdot (-4)=37. $$
Semua elemen baris pertama matriks $C$ telah ditemui. Mari kita beralih ke baris kedua, yang bermula dengan elemen $c_(21)$. Untuk mencarinya, anda perlu mendarabkan elemen baris kedua matriks $A$ dan lajur pertama matriks $B$:

$$ c_(21)=5\cdot (-9)+4\cdot 6+(-2)\cdot 7 + 1\cdot 12=-23. $$
Kami mencari elemen seterusnya $c_(22)$ dengan mendarabkan elemen baris kedua matriks $A$ dengan elemen sepadan lajur kedua matriks $B$:
$$ c_(22)=5\cdot 3+4\cdot 20+(-2)\cdot 0 + 1\cdot (-4)=91. $$
Untuk mencari $c_(31)$, darabkan unsur-unsur baris ketiga matriks $A$ dengan unsur-unsur lajur pertama matriks $B$:
$$ c_(31)=-8\cdot (-9)+11\cdot 6+(-10)\cdot 7 + (-5)\cdot 12=8. $$
Dan akhirnya, untuk mencari elemen $c_(32)$, anda perlu mendarabkan elemen baris ketiga matriks $A$ dengan elemen sepadan lajur kedua matriks $B$:
$$ c_(32)=-8\cdot 3+11\cdot 20+(-10)\cdot 0 + (-5)\cdot (-4)=216. $$
Semua elemen matriks $C$ telah ditemui, yang tinggal hanyalah menulis bahawa $C=\left(\begin(array) (cc) 0 & 37 \\ -23 & 91 \\ 8 & 216 \end( tatasusunan) \kanan)$ . Atau, untuk menulis sepenuhnya:
$$ C=A\cdot B =\left(\begin(array) (cccc) -1 & 2 & -3 & 0 \\ 5 & 4 & -2 & 1 \\ -8 & 11 & -10 & - 5 \end(array) \right)\cdot \left(\begin(array) (cc) -9 & 3 \\ 6 & 20 \\ 7 & 0 \\ 12 & -4 \end(array) \right) =\left(\begin(array) (cc) 0 & 37 \\ -23 & 91 \\ 8 & 216 \end(array) \right). $$
Jawab: $C=\left(\begin(array) (cc) 0 & 37 \\ -23 & 91 \\ 8 & 216 \end(array) \right)$.
Dengan cara ini, selalunya tiada sebab untuk menerangkan secara terperinci lokasi setiap elemen matriks hasil. Untuk matriks yang saiznya kecil, anda boleh melakukan ini:
Perlu juga diperhatikan bahawa pendaraban matriks adalah bukan komutatif. Ini bermakna dalam kes umum $A\cdot B\neq B\cdot A$. Hanya untuk beberapa jenis matriks, yang dipanggil boleh ubah(atau berulang-alik), kesamaan $A\cdot B=B\cdot A$ adalah benar. Ia adalah berdasarkan kepada bukan komutatif pendaraban yang kita perlukan untuk menunjukkan dengan tepat cara kita mendarab ungkapan dengan matriks tertentu: di sebelah kanan atau di sebelah kiri. Sebagai contoh, frasa "darab kedua-dua belah kesamaan $3E-F=Y$ dengan matriks $A$ di sebelah kanan" bermakna anda ingin mendapatkan kesamaan berikut: $(3E-F)\cdot A=Y\cdot A$.
Ditransmisikan berkenaan dengan matriks $A_(m\times n)=(a_(ij))$ ialah matriks $A_(n\times m)^(T)=(a_(ij)^(T))$, bagi unsur yang $a_(ij)^(T)=a_(ji)$.
Ringkasnya, untuk mendapatkan matriks alih alih $A^T$, anda perlu menggantikan lajur dalam matriks asal $A$ dengan baris yang sepadan mengikut prinsip ini: terdapat baris pertama - akan ada lajur pertama ; terdapat baris kedua - akan ada lajur kedua; terdapat baris ketiga - akan ada lajur ketiga dan seterusnya. Sebagai contoh, mari kita cari matriks yang ditukar kepada matriks $A_(3\times 5)$:

Sehubungan itu, jika matriks asal mempunyai saiz $3\times 5$, maka matriks transposed mempunyai saiz $5\times 3$.
Beberapa sifat operasi pada matriks.
Di sini diandaikan bahawa $\alpha$, $\beta$ ialah beberapa nombor dan $A$, $B$, $C$ ialah matriks. Untuk empat sifat pertama saya menunjukkan nama; selebihnya boleh dinamakan dengan analogi dengan empat yang pertama.
- $A+B=B+A$ (komutatif penambahan)
- $A+(B+C)=(A+B)+C$ (persekutuan penambahan)
- $(\alpha+\beta)\cdot A=\alpha A+\beta A$ (taburan pendaraban dengan matriks berkenaan dengan penambahan nombor)
- $\alpha\cdot(A+B)=\alpha A+\alpha B$ (taburan pendaraban dengan nombor berbanding dengan penambahan matriks)
- $A(BC)=(AB)C$
- $(\alpha\beta)A=\alpha(\beta A)$
- $A\cdot (B+C)=AB+AC$, $(B+C)\cdot A=BA+CA$.
- $A\cdot E=A$, $E\cdot A=A$, dengan $E$ ialah matriks identiti bagi susunan yang sepadan.
- $A\cdot O=O$, $O\cdot A=O$, dengan $O$ ialah matriks sifar dengan saiz yang sesuai.
- $\kiri(A^T \kanan)^T=A$
- $(A+B)^T=A^T+B^T$
- $(AB)^T=B^T\cdot A^T$
- $\left(\alpha A \right)^T=\alpha A^T$
Dalam bahagian seterusnya, kami akan mempertimbangkan operasi menaikkan matriks kepada kuasa integer bukan negatif, dan juga menyelesaikan contoh di mana ia perlu melakukan beberapa operasi pada matriks.
Kami akan "mengecualikan" yang tidak diketahui secara berurutan. Untuk melakukan ini, kami akan membiarkan persamaan pertama sistem tidak berubah, dan mengubah yang kedua dan ketiga:
1) kepada persamaan kedua kita menambah yang pertama, didarab dengan –2, dan membawanya ke bentuk –3 x 2 –2x 3 = –2;
2) kepada persamaan ketiga kita menambah yang pertama, didarab dengan – 4, dan membawanya ke bentuk –3 x 2 – 4x 3 = 2.
Akibatnya, yang tidak diketahui akan dikecualikan daripada persamaan kedua dan ketiga x 1 dan sistem akan mengambil borang

Kami mendarabkan persamaan kedua dan ketiga sistem dengan -1, kami dapat

Pekali 1 dalam persamaan pertama untuk yang pertama tidak diketahui X 1 dipanggil unsur peneraju langkah pertama penghapusan.
Dalam langkah kedua, persamaan pertama dan kedua kekal tidak berubah, dan kaedah yang sama untuk menghapuskan pembolehubah digunakan pada persamaan ketiga x 2 . Elemen utama daripada langkah kedua ialah pekali 3. Pada persamaan ketiga kita tambahkan yang kedua, didarab dengan –1, kemudian sistem diubah menjadi bentuk
 | (1.2) |
Proses mengurangkan sistem (1.1) kepada membentuk (1.2) dipanggil langsung kemajuan kaedah Gauss.
Prosedur untuk menyelesaikan sistem (1.2) dipanggil sebaliknya. Daripada persamaan terakhir yang kita dapat X 3 = –2. Menggantikan nilai ini ke dalam persamaan kedua, kita dapat X 2 = 2. Selepas ini, persamaan pertama memberi X 1 = 1. Oleh itu, adalah penyelesaian kepada sistem (1.1).
Konsep matriks
Mari kita pertimbangkan kuantiti yang termasuk dalam sistem (1.1). Satu set sembilan pekali berangka yang muncul sebelum yang tidak diketahui dalam persamaan membentuk jadual nombor yang dipanggil matriks:
| A= . | (1.3) |
Nombor jadual dipanggil elemen matriks. Bentuk unsur baris dan lajur matriks. Bilangan baris dan bilangan lajur terbentuk dimensi matriks. Matriks A mempunyai dimensi 3'3 (“tiga dengan tiga”), dengan nombor pertama menunjukkan bilangan baris, dan nombor kedua bilangan lajur. Selalunya matriks dilambangkan dengan menunjukkan dimensinya A (3 ´ 3). Oleh kerana bilangan baris dan lajur dalam matriks A sama, matriks dipanggil segi empat sama. Bilangan baris (dan lajur) dalam matriks segi empat sama dipanggilnya mengikut tertib, Itulah sebabnya A- matriks pesanan ketiga.
Sisi kanan persamaan juga membentuk jadual nombor, i.e. matriks:
Setiap baris matriks ini dibentuk oleh satu elemen, jadi B(3 ´ 1) dipanggil lajur matriks, dimensinya ialah 3'1. Set yang tidak diketahui juga boleh diwakili sebagai matriks lajur:
Mendarab matriks segi empat sama dengan matriks lajur
Dengan matriks adalah mungkin untuk menghasilkan pelbagai operasi, yang akan dibincangkan secara terperinci kemudian. Di sini kita hanya akan menganalisis peraturan untuk mendarab matriks segi empat sama dengan matriks lajur. Oleh takrifan, hasil pendaraban matriks A(3 ´ 3) setiap lajur DALAM(3 ´ 1) ialah lajur D(3 ´ 1) , yang unsur-unsurnya sama dengan hasil tambah bagi unsur-unsur baris matriks A kepada elemen lajur DALAM:
2)kedua elemen lajur D sama dengan jumlah hasil darab unsur kedua baris matriks A kepada elemen lajur DALAM:
Daripada formula di atas adalah jelas bahawa mendarab matriks dengan lajur DALAM hanya mungkin jika bilangan lajur matriks A sama dengan bilangan elemen dalam lajur DALAM.
Mari kita lihat dua lagi contoh berangka bagi pendaraban matriks (3 ´3) setiap lajur (3 ´1):
Contoh 1.1
AB =  .
.
Contoh 1.2
AB=  .
.
Tahun 1, matematik tinggi, belajar matriks dan tindakan asas ke atas mereka. Di sini kami mensistemkan operasi asas yang boleh dilakukan dengan matriks. Di mana untuk mula berkenalan dengan matriks? Sudah tentu, dari perkara yang paling mudah - definisi, konsep asas dan operasi mudah. Kami memberi jaminan kepada anda bahawa matriks akan difahami oleh semua orang yang menumpukan sekurang-kurangnya sedikit masa untuk mereka!
Definisi Matriks
Matriks ialah jadual unsur segi empat tepat. Nah, bagaimana jika dalam bahasa mudah– jadual nombor.
Biasanya matriks dilambangkan dengan huruf besar dengan huruf Latin. Contohnya, matriks A , matriks B dan sebagainya. Matriks boleh saiz yang berbeza: segi empat tepat, segi empat sama, terdapat juga matriks baris dan matriks lajur yang dipanggil vektor. Saiz matriks ditentukan oleh bilangan baris dan lajur. Sebagai contoh, mari kita menulis matriks segi empat tepat saiz m pada n , Di mana m – bilangan baris, dan n – bilangan lajur.

Item untuk yang i=j (a11, a22, .. ) membentuk pepenjuru utama matriks dan dipanggil pepenjuru.
Apa yang boleh anda lakukan dengan matriks? Tambah/Tolak, darab dengan nombor, membiak sesama mereka, transpose. Sekarang tentang semua operasi asas ini pada matriks mengikut urutan.
Operasi tambah dan tolak matriks
Biar kami segera memberi amaran kepada anda bahawa anda hanya boleh menambah matriks dengan saiz yang sama. Hasilnya akan menjadi matriks dengan saiz yang sama. Menambah (atau menolak) matriks adalah mudah - anda hanya perlu menambah elemen yang sepadan . Mari kita beri contoh. Mari kita laksanakan penambahan dua matriks A dan B bersaiz dua dua.

Penolakan dilakukan dengan analogi, hanya dengan tanda yang bertentangan.
hidup nombor sewenang-wenangnya Anda boleh mendarab mana-mana matriks. Untuk membuat ini, anda perlu mendarab setiap unsurnya dengan nombor ini. Sebagai contoh, mari kita darabkan matriks A daripada contoh pertama dengan nombor 5:

Operasi pendaraban matriks
Tidak semua matriks boleh didarab bersama. Sebagai contoh, kita mempunyai dua matriks - A dan B. Ia boleh didarab dengan satu sama lain hanya jika bilangan lajur matriks A adalah sama dengan bilangan baris matriks B. Dalam kes ini setiap elemen matriks yang terhasil terletak di baris ke-i dan lajur jth, akan sama dengan jumlah hasil darab unsur yang sepadan dalam baris ke-i faktor pertama dan lajur ke-j bagi kedua. Untuk memahami algoritma ini, mari tuliskan cara dua matriks persegi didarabkan:

Dan contoh dengan nombor nyata. Mari kita darabkan matriks:

Operasi transpose matriks
Transposisi matriks ialah operasi di mana baris dan lajur yang sepadan ditukar. Sebagai contoh, mari kita alihkan matriks A daripada contoh pertama:

Penentu matriks
Penentu, atau penentu, adalah salah satu konsep asas algebra linear. Suatu ketika dahulu orang datang dengan persamaan linear, dan di belakang mereka kami perlu menghasilkan penentu. Akhirnya, terpulang kepada anda untuk menangani semua ini, jadi, dorongan terakhir!
Penentu ialah ciri berangka bagi matriks segi empat sama, yang diperlukan untuk menyelesaikan banyak masalah.
Untuk mengira penentu bagi matriks persegi termudah, anda perlu mengira perbezaan antara hasil darab unsur pepenjuru utama dan sekunder.
Penentu bagi matriks tertib pertama, iaitu, terdiri daripada satu unsur, adalah sama dengan unsur ini.
Bagaimana jika matriks adalah tiga dengan tiga? Ini lebih sukar, tetapi anda boleh menguruskannya.
Untuk matriks sedemikian, nilai penentu adalah sama dengan hasil tambah unsur-unsur pepenjuru utama dan hasil darab unsur-unsur yang terletak pada segi tiga dengan muka selari dengan pepenjuru utama, dari mana hasil darab unsur pepenjuru sekunder dan hasil darab unsur yang terletak pada segi tiga dengan muka pepenjuru sekunder selari ditolak.
Nasib baik, mengira penentu matriks saiz besar dalam amalan ia jarang diperlukan.
Di sini kita melihat operasi asas pada matriks. Sudah tentu, dalam kehidupan sebenar Anda mungkin tidak pernah menemui walaupun sedikit pun sistem persamaan matriks, atau, sebaliknya, anda mungkin menghadapi kes yang lebih kompleks apabila anda benar-benar perlu memerah otak anda. Untuk kes-kes sebegini, perkhidmatan pelajar profesional wujud. Minta bantuan, dapatkan kualiti dan penyelesaian terperinci, nikmati kejayaan akademik dan masa lapang anda.
Aplikasi utama matriks adalah berkaitan dengan operasi pendaraban.
Dua matriks diberikan:
A – saiz mn
B – saiz n  k
k
Kerana panjang baris dalam matriks A bertepatan dengan ketinggian lajur dalam matriks B, anda boleh menentukan matriks C=AB, yang akan mempunyai dimensi m  k. unsur
k. unsur  matriks C, terletak dalam baris ke-i arbitrari (i=1,...,m) dan lajur ke-j arbitrari (j=1,...,k), mengikut takrifan, adalah sama dengan hasil darab skalar daripada dua vektor daripada
matriks C, terletak dalam baris ke-i arbitrari (i=1,...,m) dan lajur ke-j arbitrari (j=1,...,k), mengikut takrifan, adalah sama dengan hasil darab skalar daripada dua vektor daripada  :i-baris matriks A dan lajur ke-j matriks B:
:i-baris matriks A dan lajur ke-j matriks B:
sifat:

Bagaimanakah operasi mendarab matriks A dengan nombor λ ditakrifkan?
Hasil darab A dan nombor λ ialah matriks di mana setiap unsur adalah sama dengan hasil darab unsur A dan λ yang sepadan. Akibat: Jumlah pengganda semua elemen matriks boleh dikeluarkan daripada tanda matriks.
13. Definisi matriks songsang dan sifatnya.
Definisi. Jika terdapat matriks segi empat sama X dan A dengan susunan yang sama memenuhi syarat:
di mana E ialah matriks identiti yang sama susunan dengan matriks A, maka matriks X dipanggil terbalik kepada matriks A dan dilambangkan dengan A -1.
Sifat matriks songsang
Mari kita nyatakan sifat-sifat berikut bagi matriks songsang:
1) (A -1) -1 = A;
2) (AB) -1 = B -1 A -1
3) (A T) -1 = (A -1) T .
1. Jika matriks songsang wujud, maka ia adalah satu-satunya.
2. Tidak setiap matriks persegi bukan sifar mempunyai songsang.
14. Berikan sifat utama penentu. Semak kesahihan harta |AB|=|A|*|B| untuk matriks
A= 
 dan B=
dan B= 

Sifat penentu:
1. Jika mana-mana baris penentu terdiri daripada sifar, maka penentu itu sendiri adalah sama dengan sifar.
2. Apabila menyusun semula dua baris, penentu didarab dengan -1.
3. Penentu dengan dua baris yang sama adalah sama dengan sifar.
4. Faktor sepunya unsur-unsur mana-mana baris boleh diambil daripada tanda penentu.
5. Jika unsur-unsur baris tertentu penentu A dibentangkan sebagai hasil tambah dua sebutan, maka penentu itu sendiri adalah sama dengan hasil tambah dua penentu B dan D. Dalam penentu B, garis yang ditentukan terdiri daripada sebutan pertama, dalam D - bagi sebutan kedua. Baki garis penentu B dan D adalah sama seperti dalam A.
6. Nilai penentu tidak akan berubah jika garis lain ditambahkan pada salah satu garis, didarab dengan sebarang nombor.
7. Jumlah hasil darab unsur mana-mana baris dengan penambahan algebra kepada elemen yang sepadan pada baris yang lain adalah sama dengan 0.
8. Penentu matriks A adalah sama dengan penentu matriks terpindah A m, i.e. penentu tidak berubah apabila ditukar.
15. Takrifkan modulus dan hujah bagi nombor kompleks. Tulis nombor √3+ dalam bentuk trigonometrii, -1+ i.
Setiap nombor kompleks z=a+ib boleh dikaitkan dengan vektor (a,b)€R 2. Panjang vektor ini bersamaan dengan √a 2 + b 2 dipanggil modulus nombor kompleks z dan dilambangkan dengan |z|. Sudut φ antara vektor yang diberikan dan arah positif paksi Lembu dipanggil hujah nombor kompleks z dan dilambangkan dengan arg z.
Mana-mana nombor kompleks z≠0 boleh diwakili sebagai z=|z|(cosφ +isinφ).
Bentuk penulisan nombor kompleks ini dipanggil trigonometri.
√3+i=2(√3/2+1/2i)=2(kosπ/6+isinπ/6);
1+i=2(-√2/2+i√2/2)=2(cosπ/4+isinπ/4).
Setiap nombor kompleks Z = a + ib boleh diberikan vektor (a; b) kepunyaan R^2. Panjang vektor ini, sama dengan KB dari a^2 + b^2, dipanggil modulus nombor kompleks dan dilambangkan dengan modulus Z. Sudut antara vektor ini dan arah positif paksi Lembu dipanggil hujah nombor kompleks (ditandakan dengan arg Z).
Penambahan matriks:
Penolakan dan penambahan matriks mengurangkan kepada operasi yang sepadan pada elemen mereka. Operasi penambahan matriks dimasukkan hanya untuk matriks saiz yang sama, iaitu untuk matriks, di mana bilangan baris dan lajur adalah sama. Jumlah matriks A dan B dipanggil matriks C, yang unsur-unsurnya sama dengan jumlah unsur-unsur yang sepadan. C = A + B c ij = a ij + b ij Ditakrifkan sama perbezaan matriks.
Mendarab matriks dengan nombor:
Operasi darab (bahagi) matriks daripada sebarang saiz dengan nombor arbitrari dikurangkan kepada mendarab (membahagi) setiap elemen matriks untuk nombor ini. Produk matriks Dan nombor k dipanggil matriks B, seperti itu
b ij = k × a ij . B = k × A b ij = k × a ij . Matriks- A = (-1) × A dipanggil sebaliknya matriks A.
Sifat menambah matriks dan mendarab matriks dengan nombor:
Operasi tambah matriks Dan pendaraban matriks pada nombor mempunyai sifat berikut: 1. A + B = B + A; 2. A + (B + C) = (A + B) + C; 3. A + 0 = A; 4. A - A = 0; 5. 1 × A = A; 6. α × (A + B) = αA + αB; 7. (α + β) × A = αA + βA; 8. α × (βA) = (αβ) × A; , di mana A, B dan C ialah matriks, α dan β ialah nombor.
Pendaraban matriks (hasil matriks):
Operasi mendarab dua matriks dimasukkan hanya untuk kes apabila bilangan lajur yang pertama matriks sama dengan bilangan baris kedua matriks. Produk matriks Dan m×n pada matriks Dalam n×p, dipanggil matriks Dengan m×p sedemikian rupa sehingga dengan ik = a i1 × b 1k + a i2 × b 2k + ... + a in × b nk , iaitu, hasil tambah bagi unsur-unsur baris ke-i ditemui matriks Dan kepada elemen sepadan lajur jth matriks B. Jika matriks A dan B ialah segi empat sama yang sama saiz, maka hasil darab AB dan BA sentiasa wujud. Adalah mudah untuk menunjukkan bahawa A × E = E × A = A, di mana A ialah segi empat sama matriks, E - unit matriks saiz yang sama.

Sifat pendaraban matriks:
Pendaraban matriks bukan komutatif, i.e. AB ≠ BA walaupun kedua-dua produk ditakrifkan. Namun, jika ada matriks hubungan AB=BA berpuas hati, maka sedemikian matriks dipanggil komutatif. Contoh yang paling tipikal ialah satu matriks, yang berulang-alik dengan mana-mana yang lain matriks saiz yang sama. Hanya yang segi empat sama boleh diubah suai matriks daripada susunan yang sama. A × E = E × A = A
Pendaraban matriks mempunyai sifat-sifat berikut: 1. A × (B × C) = (A × B) × C; 2. A × (B + C) = AB + AC; 3. (A + B) × C = AC + BC; 4. α × (AB) = (αA) × B; 5. A × 0 = 0; 0 × A = 0; 6. (AB) T = B T A T; 7. (ABC) T = C T V T A T; 8. (A + B) T = A T + B T;

2. Penentu pesanan ke-2 dan ke-3. Sifat penentu.
Penentu matriks pesanan kedua, atau penentu tertib kedua ialah nombor yang dikira dengan formula:

Penentu matriks pesanan ketiga, atau penentu tertib ketiga ialah nombor yang dikira dengan formula:

Nombor ini mewakili jumlah algebra yang terdiri daripada enam sebutan. Setiap istilah mengandungi tepat satu elemen daripada setiap baris dan setiap lajur matriks. Setiap istilah terdiri daripada hasil darab tiga faktor.

Tanda dengan ahli mana penentu matriks termasuk dalam formula mencari penentu matriks tertib ketiga boleh ditentukan menggunakan skema yang diberikan, yang dipanggil peraturan segi tiga atau peraturan Sarrus. Tiga sebutan pertama diambil dengan tanda tambah dan ditentukan dari angka kiri, dan tiga sebutan berikutnya diambil dengan tanda tolak dan ditentukan dari angka kanan.
Tentukan bilangan istilah untuk dicari penentu matriks, dalam jumlah algebra, anda boleh mengira faktorial: 2! = 1 × 2 = 2 3! = 1 × 2 × 3 = 6
Sifat penentu matriks
Sifat penentu matriks:
Harta #1:
Penentu matriks tidak akan berubah jika barisnya digantikan dengan lajur, setiap baris dengan lajur dengan nombor yang sama, dan begitu juga sebaliknya (Transposisi). |A| = |A| T

Akibat:
Lajur dan Baris penentu matriks adalah sama, oleh itu, sifat yang wujud dalam baris juga dipenuhi untuk lajur.
Hartanah #2:
Apabila menyusun semula 2 baris atau lajur penentu matriks akan menukar tanda kepada yang bertentangan, mengekalkan nilai mutlak, iaitu:

Harta #3:
Penentu matriks mempunyai dua baris yang sama adalah sama dengan sifar.

Hartanah #4:
Faktor sepunya unsur bagi sebarang siri penentu matriks boleh diambil sebagai tanda penentu.

Akibat daripada hartanah No. 3 dan No. 4:
Jika semua elemen siri tertentu (baris atau lajur) adalah berkadar dengan elemen sepadan siri selari, maka penentu matriks sama dengan sifar.
Harta #5:
penentu matriks adalah sama dengan sifar, maka penentu matriks sama dengan sifar.
Hartanah #6:
Jika semua elemen baris atau lajur penentu dibentangkan sebagai jumlah 2 sebutan, maka penentu matriks boleh diwakili sebagai jumlah 2 penentu mengikut formula:

Harta #7:
Jika pada mana-mana baris (atau lajur) penentu tambah elemen yang sepadan bagi baris (atau lajur lain), didarab dengan nombor yang sama, kemudian penentu matriks tidak akan mengubah nilainya.

Contoh penggunaan sifat untuk pengiraan penentu matriks: