Seperti yang diketahui, kaedah Jordan-Gauss, juga dikenali sebagai kaedah penyingkiran berurutan yang tidak diketahui, adalah pengubahsuaian kaedah Gauss untuk menyelesaikan sistem persamaan algebra linear (SLAE).
Kaedah adalah berdasarkan transformasi asas(menterjemah sistem kepada yang setara), yang termasuk:
- menambah pada kedua-dua belah persamaan sistem persamaan lain bagi sistem yang sama, didarab dengan nombor selain sifar;
- menyusun semula persamaan dalam sistem;
- penyingkiran daripada sistem persamaan bentuk 0 = 0.
Tidak seperti kaedah Gaussian, pada setiap langkah satu pembolehubah dihapuskan daripada semua kecuali satu persamaan.
Langkah kaedah adalah seperti berikut:
- pilih yang tidak diketahui dalam persamaan seterusnya dengan pekali berbeza daripada sifar (elemen penyelesaian);
- bahagikan persamaan yang dipilih dengan elemen penyelesaian;
- menggunakan persamaan yang dipilih, kecualikan yang tidak diketahui pada elemen penyelesaian daripada semua persamaan lain;
- pada langkah seterusnya, satu lagi yang tidak diketahui juga dikecualikan daripada semua persamaan kecuali satu;
- proses berterusan sehingga semua persamaan telah digunakan.
Anda boleh membuat algoritma seperti ini:
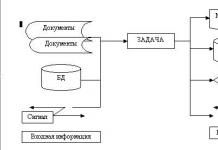
Untuk SLAU dalam bentuk matriks A*x=b (matriks A berdimensi m*n, tidak semestinya segi empat sama), jadual berikut disusun:
Elemen penyelesaian a r,s ≠0 dipilih dalam jadual, maka r ialah baris penyelesaian, s ialah lajur penyelesaian.
Peralihan ke jadual seterusnya dijalankan mengikut peraturan:
1. unsur-unsur baris penyelesaian dikira: a" r,j =a r,j /a r,s - iaitu, baris r jadual dibahagikan dengan elemen penyelesaian;
2. semua elemen lajur resolusi, kecuali r,s sama dengan satu, menjadi sama dengan sifar;
3. Elemen di luar baris dan lajur permisif dikira menggunakan formula yang ditunjukkan di bawah:

Sangat mudah untuk mengelakkan kekeliruan apabila anda melihat bahawa pengangka formula ini serupa dengan mengira penentu matriks 2-demi-2.
4. Apabila mengira secara manual, nilai dalam lajur kawalan terakhir dibandingkan dengan jumlah elemen sebelumnya garisan. Jika nilai tidak sepadan, ralat harus dicari dalam baris ini. Untuk pengiraan automatik, lajur kawalan boleh ditinggalkan.
Kes berikut adalah mungkin:
1. Dalam proses penyingkiran sebelah kiri persamaan sistem bertukar kepada 0, dan tangan kanan b≠0, maka sistem tidak mempunyai penyelesaian.
2. Identiti 0 = 0 diperoleh - persamaannya gabungan linear selebihnya dan rentetan sifar boleh dipadamkan daripada sistem.
3. Selepas menggunakan semua persamaan untuk menghapuskan yang tidak diketahui, jadual sama ada mengandungi penyelesaian yang dikehendaki atau menunjukkan ketidakkonsistenan sistem kekangan.
Mari atur cara kaedah dalam Excel menggunakan satu formula, yang sepatutnya tidak terlalu sukar untuk diubah. Contohnya, untuk menyelesaikan SLAE

Mari kita isi sel helaian dari A1 hingga D4 termasuk dengan pekali sistem, pilih elemen penyelesaian a 1,1 =1, dan buat langkah pertama kaedah dalam sel A6, di mana kita akan memasukkan formula "sejagat" untuk transformasi Jordan-Gauss:
IF(ROW($A$1)=ROW(A1);A1/$A$1;
IF(COLUMN($A$1)=COLUMN(A1),0,(A1*$A$1-
TIDAK LANGSUNG(ALAMAT(ROW(A1), COLUM($A$1)))*
TIDAK LANGSUNG(ALAMAT(BARIS($A$1), COLUM(A1)))/$A$1))

Dalam langkah seterusnya, elemen penyelesaian boleh, sebagai contoh, 2,2 =1 (sel B7). Apa yang perlu kita lakukan ialah menyalin formula dari A6 ke A11 (oleh baris kosong biarkan untuk memisahkan langkah kaedah secara visual), masukkan mod penyuntingan formula ( Klik dua kali mengikut sel atau pilihnya dan tekan kekunci F2) dan betulkan (seret tetikus dengan berhati-hati ke luar sempadan) semua pautan yang disematkan dari sel A1 ke B7.
Sudah tentu, anda boleh menggantikan rujukan yang disematkan $A$1 di mana-mana dalam formula dengan pembinaan bentuk INDIRECT(CELL) , membentuk alamat dinamik pautan. Katakan, INDIRECT(F8), dan dalam sel F8 alamat sel elemen resolusi akan dijana secara automatik oleh ditentukan oleh pengguna nombor baris dan lajur. Kemudian untuk nombor baris dan lajur ini anda perlu menyediakan sel yang berasingan, contohnya, seperti ini:

Malangnya, semua ini tidak akan memberikan apa-apa - bukannya $A$1, kita hanya perlu membetulkan INDIRECT($F$8) dalam formula dan kemudian seret dan lepaskan bilangan pautan yang sama semasa menyalin formula. Di samping itu, nombor baris dan lajur yang dimasukkan "secara manual" juga perlu disemak untuk kesahihannya (sekurang-kurangnya seperti dalam rajah), jadi kami tidak akan mendarabkan entiti.
Anda boleh melihat kaedah dalam tindakan pada dua helaian pertama yang dilampirkan Fail Excel(2 contoh berbeza).
Yang berikut juga berdasarkan transformasi Jordan-Gauss kaedah sejagat penyelesaian masalah linear pengoptimuman, bagaimana kaedah simplex. Penerangan mengenainya biasanya menakutkan, panjang dan sarat dengan teorem. Mari cuba buat penerangan ringkas dan bangunkan algoritma yang sesuai untuk pengiraan dalam Excel. Malah, kaedah simplex telah pun terbina dalam alat tambah standard Pakej analisis, dan tidak perlu memprogramkannya "secara manual", jadi kod kami mempunyai nilai pendidikan.
Pertama, minimum teori.
Jika vektor lajur SLAE adalah bebas linear, pembolehubah yang sepadan adalah asas, dan selebihnya - percuma. Contohnya, dalam SLAU

pembolehubah x 2 dan x 4 adalah asas, dan x 1 dan x 3 adalah bebas. Pembolehubah asas adalah bebas antara satu sama lain, dan yang percuma boleh dibuat, sebagai contoh, sifar dan dapatkan ( x 2 =2, x 4 =1) – penyelesaian asas sistem.
Dengan memilih elemen penyelesaian yang berbeza, adalah mungkin untuk mendapatkan penyelesaian SLAE dengan asas yang berbeza. Sebarang penyelesaian asas bukan negatif bagi SLAE dipanggil menyokong.
Kaedah simplex menyediakan peralihan daripada satu penyelesaian rujukan kepada penyelesaian rujukan yang lain sehingga ia dicapai optimum penyelesaian yang memberikan fungsi objektif minimum.
Algoritma kaedah simplex adalah seperti berikut:
1. Masalah LP diubah kepada bentuk kanonik:

Ini sentiasa boleh dilakukan seperti berikut: kepada masalah yang ditulis dalam rumusan standard

tambahan yang ditambah pembolehubah kunci kira-kira, bilangan yang sepadan dengan bilangan kekangan ketidaksamaan m (sekatan ke atas bukan negatif nilai-nilai yang tidak diketahui tidak diambil kira). Selepas ini, ketidaksamaan dengan tanda "≤" bertukar menjadi kesamaan, sebagai contoh, sistem sekatan bentuk
2*x 1 +3*x 2 ≤20
3*x 1 +x 2 ≤15
4*x 1 ≤16
3*x 2 ≤12
x 1 ,x 2 ≥0
akan mengambil borang
2*x 1 +3*x 2 +x 3 =20
3*x 1 +x 2 +x 4 =15
4*x 1 +x 5 =16
3*x 2 +x 6 =12
x 1 ,x 2 ,...,x 6 ≥0
Iaitu, makna "ekonomi" pembolehubah kunci kira-kira adalah sangat mudah - ini adalah "sisa" sumber yang tidak digunakan bagi setiap jenis.
Jika dalam masalah asal, bukan minimum, tetapi maksimum yang dicari, fungsi objektif Z akan digantikan dengan Z 1 = -Z. Penyelesaian kepada masalah bertepatan, dengan min Z = - maks Z 1 . Contohnya, matlamat
Z(x 1 ,x 2)=2*x 1 +5*x 2 (maks)
ditulis semula sebagai
Z 1 (x 1 ,x 2)=-2*x 1 -5*x 2 (min)
Jika masalah asal mempunyai persamaan ketaksamaan dengan tanda "≥" dan bukannya "≤", kedua-dua belah setiap ketaksamaan tersebut didarabkan dengan -1, dan tanda ketaksamaan diterbalikkan, contohnya,
3*x 1 +x 2 +x 4 ≥15
menjadi
3*x 1 -x 2 -x 4 ≤15
Bentuk kanonik model diperolehi, dan untuk itu kami menulis jadual simplex:

Pembolehubah asas (BP) ditulis di lajur kiri; jika ia belum dipilih, ia kosong.
2. Menggunakan langkah Jordan–Gauss, pelan rujukan awal dicari, i.e. SLAE dikurangkan kepada bentuk asasnya dengan sebutan bebas bukan negatif b i >0. Dalam kes ini, fungsi objektif Z harus dinyatakan hanya dalam bentuk tidak diketahui bebas (pekali sifar dalam baris Z hanya di bawah pembolehubah x i yang berada dalam asas). Apabila memilih elemen penyelesaian a r,s, kami menulis pembolehubah x s dalam baris r lajur BP; jika sudah ada pembolehubah di sana, kami memotongnya (kami mengeluarkannya dari asas).
3. Kami menulis pelan rujukan X * di bawah lajur x i: di bawah pembolehubah bebas - sifar, di bawah pembolehubah asas - pekali dari lajur b sepadan dengan pembolehubah asas.
Di bawah kita tuliskan vektor R mengikut peraturan: di bawah pembolehubah asas terdapat sifar, di bawah yang bebas R i =Z i .
Jika semua R i ≥0, penyelesaian optimum X * dan nilai matlamat Z min = -q ditemui, jika tidak, kita perlu rancangan baru, adakah anda memilikinya, Komrad Zhyukov? (fasal 4).
4. Untuk memilih lajur penyelesaian s, pilih komponen negatif mutlak maksimum bagi vektor R, lajur penyelesaian s dipilih. Kemudian kami menganalisis pekali lajur sth matriks sistem sekatan. Jika semua a i,s ≤0, tiada penyelesaian dan Z min cenderung kepada tolak infiniti, jika tidak pergi ke langkah 5.
5. Untuk memilih rentetan penyelesaian r, kami menyusun hubungan bukan negatif b i /A i,s ≥0, i=1,2,...,m, dan pilih yang terkecil di antara mereka. Jika minimum dicapai untuk beberapa baris, mana-mana daripadanya boleh dianggap sebagai penyelesaian, dan dalam pelan rujukan baharu nilai beberapa pembolehubah asas akan menjadi sama dengan 0, iaitu, kita memperoleh pelan rujukan yang merosot.
6. Kami melakukan transformasi Jordan-Gauss dengan elemen penyelesaian a r,s dan pergi ke langkah 3
Secara geometri, kaedah simpleks sepadan dengan traversal terpendek bagi bucu polihedron cembung n-dimensi, yang membentuk kawasan penyelesaian yang boleh dilaksanakan kepada masalah:

Di sini kita bergerak dari pelan rujukan C, yang merupakan salah satu bucu poligon berbilang dimensi, kepada rancangan yang optimum E=X * .
Memprogramkan semua ini dalam Excel bukanlah mudah, tetapi ia mungkin. Dokumen yang dilampirkan menyediakan 3 contoh yang melaksanakan penyelesaian masalah menggunakan kaedah simpleks. Benar, apabila melakukan langkah itu, anda sudah perlu menukar 3 formula; pada helaian contoh pertama untuk kaedah simpleks ia diserlahkan dalam warna kuning: mengira hubungan untuk memilih baris penyelesaian dalam sel I2, mengisi lajur BP dalam sel A12, langkah transformasi Jordan-Gauss dalam sel B12. Seperti dalam contoh transformasi Jordan-Gauss, menukar formula hanya dikaitkan dengan keperluan untuk merujuk baris baru, mengandungi alamat sel dengan elemen pemboleh (untuk langkah pertama - sel C9).
. Algoritma kaedah simplex
Contoh 5.1. Selesaikan masalah berikut pengaturcaraan linear kaedah simplex:
Penyelesaian:
saya lelaran:

x3, x4, x5, x6 x1,x2. Mari kita nyatakan pembolehubah asas dari segi pembolehubah percuma:

Mari kita kurangkan fungsi sasaran kepada pandangan seterusnya:
Berdasarkan masalah yang diperoleh, kami akan membentuk jadual simpleks awal:
Jadual 5.3
Jadual simplex asal
Hubungan Evaluatif |
||||
Menurut definisi penyelesaian asas, pembolehubah bebas adalah sama dengan sifar, dan nilai pembolehubah asas adalah sama dengan nilai sepadan nombor bebas, iaitu:
Peringkat 3: menyemak keserasian sistem sekatan PAP.
Pada lelaran ini (dalam Jadual 5.3), tanda ketidakkonsistenan sistem kekangan (tanda 1) tidak dikenal pasti (iaitu tiada garis dengan nombor bebas negatif (kecuali untuk garis fungsi objektif) yang tidak akan menjadi sekurang-kurangnya satu elemen negatif (iaitu pekali negatif untuk pembolehubah bebas)).
Pada lelaran ini (dalam Jadual 5.3), tanda ketakterbatasan fungsi objektif (tanda 2) tidak dikenal pasti (iaitu, tiada lajur dengan unsur negatif dalam baris fungsi objektif (kecuali lajur nombor bebas). ) di mana tidak akan ada sekurang-kurangnya satu unsur positif) .
Oleh kerana penyelesaian asas yang ditemui tidak mengandungi komponen negatif, ia boleh diterima.
Peringkat 6: semakan optimum.
Penyelesaian asas yang ditemui tidak optimum, kerana mengikut kriteria optimum (tanda 4) seharusnya tidak ada unsur negatif dalam baris fungsi objektif ( nombor percuma baris ini tidak diambil kira apabila mempertimbangkan ciri ini). Oleh itu, mengikut algoritma kaedah simplex, kita beralih ke peringkat 8.
Oleh kerana penyelesaian asas yang ditemui boleh diterima, kami akan mencari lajur penyelesaian mengikut skema berikut: kami menentukan lajur dengan unsur negatif dalam baris fungsi objektif (kecuali lajur nombor bebas). Menurut Jadual 5.3, terdapat dua lajur tersebut: lajur “ x1"dan lajur" x2" Daripada lajur sedemikian, lajur yang mengandungi elemen terkecil dalam baris fungsi sasaran dipilih. Dia akan menjadi yang permisif. Kolum " x2" mengandungi unsur terkecil (–3) berbanding lajur " x1
Untuk menentukan garis penyelesaian, kita dapati nisbah anggaran positif nombor bebas kepada unsur lajur penyelesaian; garisan yang sepadan dengan nisbah penilaian positif terkecil diterima sebagai diselesaikan.
Jadual 5.4
Jadual simplex asal
Dalam Jadual 5.4, hubungan penilaian positif terkecil sepadan dengan garis " x5", oleh itu, ia akan menjadi permisif.
Elemen yang terletak di persimpangan lajur pemboleh dan baris pemboleh diterima sebagai pemboleh. Dalam contoh kami, ini ialah elemen yang terletak di persimpangan garis " x5"dan lajur" x2».
Elemen penyelesaian menunjukkan satu asas dan satu pembolehubah bebas yang mesti ditukar dalam jadual simplex untuk beralih kepada penyelesaian asas "diperbaiki" yang baharu. DALAM dalam kes ini ini adalah pembolehubah x5 Dan x2, dalam jadual simplex baharu (Jadual 5.5) kami menukarnya.
9.1. Transformasi unsur penyelesaian.
Elemen resolusi Jadual 5.4 ditukar seperti berikut:
![]()
Kami memasukkan hasil yang terhasil ke dalam sel yang serupa dalam Jadual 5.5.
9.2. Penukaran rentetan resolusi.
Kami membahagikan elemen baris penyelesaian jadual 5.4 dengan elemen penyelesaian jadual simpleks ini, hasilnya sesuai dengan sel yang serupa dalam jadual simpleks baharu (jadual 5.5). Transformasi elemen rentetan resolusi diberikan dalam Jadual 5.5.
9.3. Penukaran lajur resolusi.
Kami membahagikan elemen lajur resolusi jadual 5.4 dengan elemen resolusi jadual ringkas ini, dan hasilnya diambil daripada tanda bertentangan. Keputusan yang diperolehi dimuatkan ke dalam sel yang serupa pada jadual simpleks baharu (Jadual 5.5). Transformasi unsur-unsur lajur resolusi diberikan dalam Jadual 5.5.
9.4. Transformasi unsur-unsur baki jadual simpleks.
Transformasi unsur-unsur baki jadual simpleks (iaitu, elemen yang tidak terletak dalam baris penyelesaian dan lajur penyelesaian) dijalankan mengikut peraturan "segi empat tepat".
Sebagai contoh, pertimbangkan untuk menukar elemen yang terletak di persimpangan garis " x3" dan lajur "", kami akan menyatakannya secara bersyarat " x3" Dalam Jadual 5.4, kita secara mental melukis segi empat tepat, satu bucunya terletak di dalam sel yang nilainya kita ubah (iaitu dalam sel " x3"), dan satu lagi (bucu pepenjuru) berada dalam sel dengan elemen penyelesaian. Dua bucu yang lain (pada pepenjuru kedua) ditentukan secara unik. Kemudian nilai berubah sel " x3" akan sama dengan nilai sebelumnya sel ini tolak pecahan, dalam penyebutnya ialah elemen penyelesaian (daripada Jadual 5.4), dan dalam pengangka ialah hasil darab dua bucu lain yang tidak digunakan, iaitu:
« x3»: .
Nilai sel lain ditukar sama:
« x3 x1»: ;
« x4»: ![]() ;
;
« x4 x1»: ;
« x6»: ![]() ;
;
« x6 x1»: ;
«»: ![]() ;
;
« x1»: ![]() .
.
Hasil daripada transformasi ini, kami menerima yang baharu jadual simplex(Jadual 5.5).
II lelaran:
Peringkat 1: merangka jadual simpleks.
Jadual 5.5
Jadual simplexII lelaran
Dianggarkan perhubungan |
||||
| ||||
|
|
Peringkat 2: penentuan penyelesaian asas.
Hasil daripada penjelmaan simpleks, penyelesaian asas baru diperolehi (Jadual 5.5):
Seperti yang anda lihat, dengan penyelesaian asas ini nilai fungsi objektif = 15, yang lebih besar daripada penyelesaian asas sebelumnya.
Ketidakkonsistenan sistem sekatan mengikut ciri 1 dalam Jadual 5.5 belum dikenal pasti.
Peringkat 4: menyemak sempadan fungsi objektif.
Ketakterbatasan fungsi objektif mengikut kriteria 2 dalam Jadual 5.5 tidak didedahkan.
Peringkat 5: menyemak kebolehterimaan penyelesaian asas yang ditemui.
Penyelesaian asas yang ditemui mengikut kriteria 4 tidak optimum, kerana garis fungsi objektif jadual simpleks (Jadual 5.5) mengandungi unsur negatif: –2 (nombor bebas baris ini tidak diambil kira apabila mempertimbangkan ini ciri). Oleh itu, kita beralih ke peringkat 8.
Peringkat 8: penentuan elemen penyelesaian.
8.1. Definisi lajur resolusi.
Penyelesaian asas yang ditemui boleh diterima; kami menentukan lajur dengan unsur negatif dalam baris fungsi objektif (kecuali lajur nombor bebas). Menurut Jadual 5.5, terdapat hanya satu lajur sedemikian: “ x1" Oleh itu, kami menerimanya seperti yang dibenarkan.
8.2. Definisi rentetan dayakan.
Mengikut nilai yang diperolehi hubungan penilaian positif dalam Jadual 5.6, minimum ialah hubungan yang sepadan dengan garis " x3" Oleh itu, kami menerimanya seperti yang dibenarkan.
Jadual 5.6
Jadual simplexII lelaran
Dianggarkan perhubungan |
||||
3/1=3 – min |
||||
Peringkat 9: penjelmaan jadual simpleks.
Transformasi jadual simplex (Jadual 5.6) dilakukan dengan cara yang sama seperti dalam lelaran sebelumnya. Keputusan penjelmaan unsur jadual simpleks diberikan dalam Jadual 5.7.
III lelaran
Berdasarkan hasil transformasi simpleks lelaran sebelumnya, kami menyusun jadual simpleks baharu:
Jadual 5.7
Jadual simplexIII lelaran
Dianggarkan perhubungan |
||||
| ||||
|
|
Peringkat 2: penentuan penyelesaian asas.
Hasil daripada penjelmaan simpleks, penyelesaian asas baru diperolehi (Jadual 5.7):
Peringkat 3: menyemak keserasian sistem sekatan.
Ketidakkonsistenan sistem sekatan mengikut ciri 1 dalam Jadual 5.7 belum dikenal pasti.
Peringkat 4: menyemak sempadan fungsi objektif.
Ketakterbatasan fungsi objektif mengikut kriteria 2 dalam Jadual 5.7 tidak didedahkan.
Peringkat 5: menyemak kebolehterimaan penyelesaian asas yang ditemui.
Penyelesaian asas yang ditemui mengikut kriteria 3 boleh diterima, kerana ia tidak mengandungi komponen negatif.
Peringkat 6: menyemak optimum penyelesaian asas yang ditemui.
Penyelesaian asas yang ditemui mengikut kriteria 4 tidak optimum, kerana garis fungsi objektif jadual simpleks (Jadual 5.7) mengandungi unsur negatif: –3 (nombor bebas baris ini tidak diambil kira apabila mempertimbangkan ini ciri). Oleh itu, kita beralih ke peringkat 8.
Peringkat 8: penentuan elemen penyelesaian.
8.1. Definisi lajur resolusi.
Penyelesaian asas yang ditemui boleh diterima; kami menentukan lajur dengan unsur negatif dalam baris fungsi objektif (kecuali lajur nombor bebas). Menurut Jadual 5.7, terdapat hanya satu lajur sedemikian: “ x5" Oleh itu, kami menerimanya seperti yang dibenarkan.
8.2. Definisi rentetan dayakan.
Menurut nilai yang diperolehi hubungan penilaian positif dalam Jadual 5.8, minimum ialah hubungan yang sepadan dengan garis " x4" Oleh itu, kami menerimanya seperti yang dibenarkan.
Jadual 5.8
Jadual simplexIII lelaran
Dianggarkan perhubungan |
||||
5/5=1 – min |
||||
Peringkat 9: penjelmaan jadual simpleks.
Transformasi jadual simpleks (Jadual 5.8) dilakukan dengan cara yang sama seperti dalam lelaran sebelumnya. Keputusan penjelmaan unsur jadual simpleks diberikan dalam Jadual 5.9.
IV lelaran
Peringkat 1: pembinaan jadual simpleks baharu.
Berdasarkan hasil transformasi simpleks lelaran sebelumnya, kami menyusun jadual simpleks baharu:
Jadual 5.9
Jadual simplexIV lelaran
Dianggarkan perhubungan |
||||
| –(–3/5)=3/5 | |||
–(1/5)=–1/5 | ||||
| –(9/5)=–9/5 | |||
|
| –(–3/5)=3/5 |
Peringkat 2: penentuan penyelesaian asas.
Hasil daripada penjelmaan simpleks, penyelesaian asas baharu telah diperoleh; mengikut Jadual 5.9, penyelesaiannya adalah seperti berikut:
Peringkat 3: menyemak keserasian sistem sekatan.
Ketidakkonsistenan sistem sekatan mengikut ciri 1 dalam Jadual 5.9 belum dikenal pasti.
Peringkat 4: menyemak sempadan fungsi objektif.
Ketakterbatasan fungsi objektif mengikut kriteria 2 dalam Jadual 5.9 tidak didedahkan.
Peringkat 5: menyemak kebolehterimaan penyelesaian asas yang ditemui.
Penyelesaian asas yang ditemui mengikut kriteria 3 boleh diterima, kerana ia tidak mengandungi komponen negatif.
Peringkat 6: menyemak optimum penyelesaian asas yang ditemui.
Penyelesaian asas yang ditemui mengikut ciri 4 adalah optimum, kerana tiada unsur negatif dalam baris fungsi objektif jadual simpleks (Jadual 5.9) (nombor bebas baris ini tidak diambil kira apabila mempertimbangkan ciri ini) .
Peringkat 7: menyemak alternatif penyelesaian.
Penyelesaian yang ditemui adalah unik, kerana garis fungsi objektif (Jadual 5.9) tidak mengandungi unsur sifar(nombor bebas baris ini tidak diambil kira apabila mempertimbangkan ciri ini).
Jawapan: nilai optimum fungsi objektif masalah yang sedang dipertimbangkan =24, yang dicapai pada.
Contoh 5.2. Selesaikan masalah pengaturcaraan linear di atas dengan syarat fungsi objektif diminimumkan:
Penyelesaian:
saya lelaran:
Peringkat 1: pembentukan jadual simpleks awal.
Masalah pengaturcaraan linear asal diberikan dalam bentuk piawai. Marilah kita membawanya ke bentuk kanonik dengan memperkenalkan pembolehubah bukan negatif tambahan ke dalam setiap kekangan ketidaksamaan, i.e.

Dalam sistem persamaan yang terhasil, kami mengambil pembolehubah (asas) yang dibenarkan x3, x4, x5, x6, maka pembolehubah bebas ialah x1,x2. Mari kita nyatakan pembolehubah asas dari segi pembolehubah percuma.
Baca juga:
|
Teorem (tentang pilihan unsur penyelesaian)
Jika beberapa lajur baris ke-z mempunyai unsur negatif, maka lajur penyelesaian mesti dipilih untuk menjadi lajur dengan hasil maksimum nilai mutlak pekali dalam baris ke-z dan nisbah simpleks minimum lajur ini.
Bukti:
Biarkan elemen itu menjadi elemen yang membenarkan. Hasil daripada langkah penyingkiran Jordan yang diubah suai, sebutan bebas dalam baris-z ialah nombor yang sama dengan . Oleh kerana dan , kurungan dalam ungkapan ini akan sentiasa positif. Dan oleh kerana nilai fungsian sentiasa sama dengan istilah bebas, kurungan ini mewakili penambahan fungsi yang diperoleh hasil daripada langkah yang diambil.
Semakin besar peningkatan fungsi yang diterima pada setiap langkah, semakin sedikit langkah (iaitu, pengiraan) diperlukan untuk mencapai tahap optimum. Magnitud kenaikan ini bergantung pada nilai mutlak pekali dan pada nilai nisbah simpleks terkecil. Iaitu, lajur penyelesaian akan menjadi lajur yang mempunyai maksimum produk ini.
Contoh: pengaturcaraan linear:
Mari cari fungsi maksimum
di bawah sekatan
Penyelesaian: Mari buat jadual Jordan.
Memandangkan ahli bebasnya adalah positif, rancangan itu adalah yang menyokong. Walau bagaimanapun, ia tidak optimum kerana pekali z-row adalah negatif. Kami memilih daripada mereka yang mempunyai produk terbesar dengan nilai mutlak dan nisbah ringkas terkecil. Lajur ketiga dianggap menyelesaikan, kerana ia mempunyai yang terbesar nilai mutlak 8 dan hubungan simpleks: masing-masing ( , jadi elemen 1 dalam lajur ketiga akan diselesaikan). Kami mengambil langkah penyingkiran Jordan yang diubah suai dan tiba di jadual berikut.
Berdasarkan pekali z-row, jadual yang terhasil tidak mencapai penyelesaian optimum. Kami mengambil lajur kedua dengan pekali negatif dalam baris-z sebagai penyelesaian (hanya yang pertama boleh menjadi baris penyelesaian). Dengan unsur 5 ditemui, kami mengambil langkah seterusnya.
Dalam baris-z, semua pekali adalah positif; reka bentuk yang diperoleh dengan menyamakan pembolehubah atas kepada sifar dan pembolehubah sisi kepada sebutan bebas adalah optimum. Kami menulis nilai-nilai yang tidak diketahui utama dari jadual: Nilai maksimum Kami mengira kefungsian dalam sel terakhir jadual:
Dalam jadual akhir semua penentu adalah bukan negatif. Ini menunjukkan bahawa untuk nilai yang tidak diketahui fungsinya mencapai maksimum
Biasanya diandaikan bahawa tiada titik dalam set rancangan masalah di mana penyebut fungsi objektif adalah sama dengan sifar. Tanpa kehilangan sifat umum, kita boleh menganggap bahawa .
Dalam masalah pengaturcaraan linear pecahan, keterlaluan fungsi objektif dicapai pada puncak polihedron larutan. Persamaan dengan pengaturcaraan linear ini membolehkan masalah linear pecahan diselesaikan menggunakan kaedah Stiefel.
Pengiraan dibentangkan dalam bentuk jadual Jordan. Dalam kes ini, dua baris bawah diperuntukkan untuk fungsi: pada yang pertama kita menulis pekali pengangka, dan pada yang kedua - penyebut. Tugas asal sepadan dengan jadual 1:
| –x 1 | –x 2 | … | –x j | … | –x n | ||
| y 1 | a 11 | a 12 | … | a 1 j | … | a 1 n | a 1 |
| … | ……………………………………… | … | |||||
| y i | a i 1 | a i 2 | … | a ij | … | a dalam | a i |
| … | ……………………………………… | … | |||||
| y m | a m 1 | a m 2 | … | seorang mj | … | seorang mn | a m |
| z 1 | –hlm 1 | –hlm 2 | … | –p j | … | –p n | |
| z 2 | –q 1 | –q 2 | … | –q j | … | –qn |
Melalui y i perbezaan antara bahagian kanan dan kiri sistem sekatan ditunjukkan:
y i= a i–a i 1 x 1 – a i 2 x 2 –a i 3 x 3 – … – a dalam x n ³ 0.
Kami akan memanggil pembolehubah bebas pembolehubah yang terletak di baris tajuk atas jadual Jordan. Dengan memberikan nilai sifar kepada pembolehubah bebas, kami memperoleh penyelesaian asas awal: . Vektor ini tidak boleh menjadi pelan rujukan, kerana penyebut bagi fungsi objektif padanya adalah sama dengan sifar ( z 2 = 0). Oleh itu, antara ahli bebas sistem sekatan a 1 ,…, a m mesti ada nombor negatif (jika tidak penyelesaian asas akan menjadi pelan rujukan).
Dengan langkah-langkah penyingkiran Jordan yang diubah suai, dengan cara yang sama seperti semasa menyelesaikan masalah pengaturcaraan linear (lihat), kami dapati rancangan asal masalah itu. Akibatnya k langkah kami tiba di jadual 2:
| –y 1 | … | –x j | … | –x n | ||
| x 1 | b 11 | … | b 1 j | … | b 1 n | b 1 |
| .… | ……………………………………… | |||||
| y i | b i 1 | … | b ij | … | b dalam | b i |
| …. | ……………………………………. | |||||
| y m | b m 1 | … | b mj | … | b mn | b m |
| z 1 | f 1 | … | f j | … | fn | F |
| z 2 | g 1 | … | g j | … | g n | G |
Dalam jadual 2 semua ahli percuma b i adalah bukan negatif, yang memastikan bukan negatif pembolehubah asas x 1 ,…, y m. Di samping itu (disebabkan penyebut positif fungsi objektif z 2 pada satu set pelan rujukan). Pelan rujukan awal ialah vektor dengan koordinat . Nilai fungsi objektif pada pelan rujukan asal ialah .
Ambil perhatian bahawa jika di salah satu penyingkiran Jordan langkah mana-mana syarat percuma b saya akan menjadi negatif, dan semua elemen lain i baris ke tidak akan menjadi tidak negatif, maka masalah tidak akan mempunyai penyelesaian kerana kekurangan rancangan.
Mari lihat bagaimana fungsi objektif berubah apabila berpindah dari satu pelan rujukan masalah kepada yang lain. Ternyata tanda perbezaan antara nilai baru dan lama fungsi bertepatan dengan tanda penentu. Jika. Kerana Oleh kerana polyhedron penyelesaian hanya mengandungi bilangan pelan sokongan yang terhingga, maka dalam bilangan langkah yang terhingga kita akan sampai pada pelan sokongan yang optimum.
Proses ini hanya boleh dihalang oleh ketidakterbatasan polihedron larutan. Dalam kes ini, fungsi objektif mungkin mempunyai apa yang dipanggil asymptotic extremum (dalam kes ini, maksimum). Maksimum asimptotik masalah pengaturcaraan linear pecahan ialah sempadan atas tepat bagi fungsi objektif pada set rancangan, yang tidak dicapai pada mana-mana rancangan. Dalam kes apabila masalah mempunyai maksimum tanpa gejala, dalam bidang rancangan adalah sentiasa mungkin untuk mencari rancangan (bukan rujukan) di mana fungsi objektif mengambil nilai sewenang-wenangnya dekat dengan maksimum tanpa gejala.
Kaedah Stiefel membolehkan anda mencari bukan sahaja maksimum, tetapi juga maksimum asimptotik masalah pengaturcaraan linear pecahan. Mari kita lihat dengan lebih dekat peralihan daripada pelan ke pelan dan ketahui. Memilih elemen penyelesaian dalam j lajur ke-, kita mesti berpandukan prinsip hubungan simpleks minimum. Itu. elemen pemboleh dalam j Lajur -th mestilah dalam baris yang perhubungan simpleksnya positif dan minimum.
Kerana selepas mencari pelan rujukan awal, semua bahagian sebelah kanan b i menjadi bukan negatif, kemudian elemen penyelesaian j Lajur ke boleh menjadi salah satu unsur positifnya (). Jika pada setiap langkah peringkat carian untuk pelan rujukan optimum terdapat (sekurang-kurangnya satu) elemen positif dalam lajur resolusi yang dipilih, maka masalah sedemikian mempunyai maksimum (mungkin lebih daripada satu).
Walau bagaimanapun, jika pada salah satu langkah beberapa anggaran adalah kurang daripada sifar, dan semua elemen j lajur ke. Kemudian dalam lajur ini, berpandukan prinsip hubungan simpleks minimum, elemen penyelesaian tidak boleh dipilih. Meningkatkan nilai pembolehubah bebas x j dari 0 hingga (lihat Jadual 2), kami kekal dalam bidang rancangan sepanjang masa. Ini disebabkan oleh fakta bahawa peningkatan dalam pembolehubah x j tidak menyebabkan perubahan tanda kepada tolak untuk mana-mana pembolehubah asas.
Mari kita nyatakan dengan M had yang, meningkat secara monoton, fungsi objektif cenderung pada: . Nombor ini adalah maksimum tanpa gejala.
| 2 |
Kaedah Gauss-Jordan bertujuan untuk menyelesaikan sistem persamaan algebra linear (SLAE). Ia adalah pengubahsuaian kaedah Gauss. Jika kaedah Gauss dijalankan dalam dua peringkat (ke hadapan dan ke belakang), maka kaedah Gauss-Jordan membolehkan anda menyelesaikan sistem dalam satu peringkat. Butiran dan aplikasi langsung kaedah Gauss-Jordan diterangkan dalam contoh.
Dalam semua contoh, $A$ menandakan matriks sistem, $\widetilde(A)$ matriks sistem lanjutan. Anda boleh membaca tentang bentuk matriks rakaman SLAE.
Contoh No. 1
Selesaikan SLAE $ \left\( \begin(aligned) & 4x_1-7x_2+8x_3=-23;\\ & 2x_1-4x_2+5x_3=-13;\\ & -3x_1+11x_2+x_3=16. \end(aligned ) \kanan.$ dengan kaedah Gauss-Jordan.
Mari beralih dari matriks terakhir yang kami terima ke sistem:
$$ \left\( \begin(aligned) & 0\cdot x_1+1\cdot x_2+0\cdot x_3=1;\\ & 1\cdot x_1+0\cdot x_2+0\cdot x_3=-2; \\ & 0\cdot x_1+0\cdot x_2+1\cdot x_3=-1. \end(diselaraskan) \kanan. $$
Memudahkan sistem yang terhasil, kami mempunyai:
$$ \kiri\( \mulakan(dijajar) & x_2=1;\\ & x_1=-2;\\ & x_3=-1. \end(diselaraskan) \kanan. $$
Penyelesaian lengkap tanpa penjelasan ia kelihatan seperti ini:

Walaupun kaedah memilih elemen penyelesaian ini agak boleh diterima, adalah lebih baik untuk memilih unsur pepenjuru matriks sistem sebagai elemen penyelesaian. Kami akan melihat kaedah ini di bawah.
Pemilihan elemen penyelesaian pada pepenjuru utama matriks sistem.
Memandangkan kaedah penyelesaian ini benar-benar serupa dengan yang sebelumnya (kecuali untuk pemilihan elemen pemboleh), kami akan melangkau penjelasan terperinci. Prinsip memilih elemen yang membolehkan adalah mudah: dalam lajur pertama kita memilih elemen baris pertama, dalam lajur kedua kita mengambil elemen baris kedua, dalam lajur ketiga kita mengambil elemen baris ketiga, dan sebagainya. pada.
Langkah pertama
Dalam lajur pertama, pilih elemen baris pertama, i.e. kita mempunyai elemen 4 sebagai elemen penyelesaian. Saya faham bahawa memilih nombor 2 nampaknya lebih baik, kerana nombor ini masih kurang daripada 4. Agar nombor 2 dalam lajur pertama berpindah ke tempat pertama, mari kita tukar yang pertama dan baris kedua:
$$ \kiri(\mulakan(susun) (ccc|c) 4 & -7 & 8 & -23\\ 2 & -4& 5 & -13 \\ -3 & 11 & 1 & 16 \tamat(tatasusunan) \ kanan)\anak panah kanan \kiri(\mulakan(susun) (ccc|c) 2 & -4& 5 & -13\\ 4 & -7 & 8 & -23 \\ -3 & 11 & 1 & 16 \tamat(tatasusunan ) \kanan)$$
Jadi, elemen pemboleh diwakili oleh nombor 2. Dengan cara yang sama seperti sebelumnya, bahagikan baris pertama dengan 2, dan kemudian tetapkan semula elemen lajur pertama kepada sifar:
$$ \left(\mulakan(array) (ccc|c) 2 & -4& 5 & -13\\ 4 & -7 & 8 & -23 \\ -3 & 11 & 1 & 16 \end(array) \ kanan) \begin(array) (l) I:2 \\\phantom(0) \\ \phantom(0) \end(array) \rightarrow \left(\begin(array) (ccc|c) 1 & - 2& 5/2 & -13/2 \\4 & -7 & 8 & -23\\ -3 & 11 & 1 & 16 \end(array) \kanan) \mula(array) (l) \phantom(0 ) \\ II-4\cdot I\\ III+3\cdot I \end(array) \rightarrow \left(\begin(array) (ccc|c) 1 & -2& 5/2 & -13/2\ \0 & 1 & -2 & 3\\ 0 & 5 & 17/2 & -7/2 \end(array) \kanan). $$
Langkah kedua
Langkah kedua memerlukan sifar unsur-unsur lajur kedua. Kami memilih elemen baris kedua sebagai elemen penyelesaian, i.e. 1. Elemen penyelesaian sudah sama dengan satu, jadi kami tidak akan menukar sebarang baris. Ngomong-ngomong, jika kami ingin menukar baris, kami tidak akan menyentuh baris pertama, kerana ia telah digunakan dalam langkah pertama. Tetapi baris kedua dan ketiga boleh ditukar dengan mudah. Walau bagaimanapun, saya ulangi, dalam keadaan ini tidak perlu menukar garisan, kerana elemen penyelesaian sudah optimum - ia sama dengan satu.
$$ \kiri(\mulakan(tatasusunan) (ccc|c) 1 & -2& 5/2 & -13/2\\0 & 1 & -2 & 3\\ 0 & 5 & 17/2 & -7/ 2 \end(array) \right) \begin(array) (l) I+2\cdot II \\ \phantom(0)\\ III-5\cdot II \end(array) \rightarrow \left(\begin (tatasusunan) (ccc|c) 1 & 0 & -3/2 & -1/2 \\ 0 & 1 & -2 & 3\\ 0 & 0 & 37/2 & -37/2 \end(array) \kanan). $$
Langkah kedua selesai. Mari kita teruskan ke langkah ketiga.
Langkah ketiga
Langkah ketiga memerlukan sifar elemen lajur ketiga. Sebagai elemen penyelesaian, kami memilih elemen baris ketiga, i.e. 37/2. Mari bahagikan elemen baris ketiga dengan 37/2 (supaya elemen penyelesaian menjadi sama dengan 1), dan kemudian tetapkan semula elemen sepadan lajur ketiga kepada sifar:
$$ \left(\begin(array) (ccc|c) 1 & 0 & -3/2 & -1/2 \\ 0 & 1 & -2 & 3\\ 0 & 0 & 37/2 & -37 /2 \end(array) \kanan) \begin(array) (l) \phantom(0)\\ \phantom(0)\\ III:\frac(37)(2) \end(array) \rightarrow \ kiri(\mulakan(tatasusunan) (ccc|c) 1 & 0 & -3/2 & -1/2 \\ 0 & 1 & -2 & 3\\ 0 & 0 & 1 & -1 \end(tatasusunan) \kanan) \begin(array) (l) I+2\cdot III\\II+3/2\cdot III\\ \phantom(0) \end(array) \rightarrow \left(\begin(array) ( ccc|c) 1 & 0 & 0 & -2 \\ 0 & 1 & 0 & 1\\ 0 & 0 & 1 & -1 \end(array) \right). $$
Jawapan diterima: $x_1=-2$, $x_2=1$, $x_3=-1$. Penyelesaian lengkap tanpa penjelasan kelihatan seperti ini:

Semua contoh lain pada halaman ini akan diselesaikan dengan cara kedua: kami akan memilih elemen pepenjuru matriks sistem sebagai elemen penyelesaian.
Jawab: $x_1=-2$, $x_2=1$, $x_3=-1$.
Contoh No. 2
Selesaikan SLAE $ \left\( \begin(aligned) & 3x_1+x_2+2x_3+5x_4=-6;\\ & 3x_1+x_2+2x_4=-10;\\ & 6x_1+4x_2+11x_3+11x_4=-27; \\ & -3x_1-2x_2-2x_3-10x_4 = 1. \end(aligned) \right.$ dengan kaedah Gauss-Jordan.
Mari kita tulis matriks lanjutan sistem ini: $\widetilde(A)=\left(\begin(array) (cccc|c) 3 & 1 & 2 & 5 & -6\\ 3 & 1& 0 & 2 & -10 \\ 6 & 4 & 11 & 11 & -27 \\ -3 & -2 & -2 & -10 & 1 \end(array) \kanan)$.
Kami akan memilih elemen pepenjuru matriks sistem sebagai elemen penyelesaian: pada langkah pertama kami akan mengambil elemen baris pertama, pada langkah kedua kami akan mengambil elemen baris kedua, dan seterusnya.
Langkah pertama
Kita perlu menetapkan semula elemen yang sepadan bagi lajur pertama. Mari kita ambil elemen baris pertama sebagai elemen penyelesaian, i.e. 3. Oleh itu, baris pertama perlu dibahagikan dengan 3 supaya elemen penyelesaian menjadi sama dengan satu. Dan kemudian tetapkan semula semua elemen lajur pertama, kecuali yang membenarkan:
$$ \left(\begin(array)(cccc|c) 3 & 1 & 2 & 5 & -6\\ 3 & 1 & 0 & 2 & -10\\ 6 & 4 & 11 & 11 & -27\ \ -3 & -2 & -2 & -10 & 1\end(array)\kanan) \begin(array) (l) I:3\\ \phantom(0)\\\phantom(0)\\\ phantom(0)\end(array) \rightarrow \left(\begin(array)(cccc|c) 1 & 1/3 & 2/3 & 5/3 & -2\\ 3 & 1 & 0 & 2 & -10\\ 6 & 4 & 11 & 11 & -27\\ -3 & -2 & -2 & -10 & 1\end(array)\kanan) \mula(array) (l) \phantom(0) \\ II-3\cdot I\\III-6\cdot I\\IV+3\cdot I\end(array) \rightarrow\\ \rightarrow\left(\begin(array)(cccc|c) 1 & 1/3 & 2/3 & 5/3 & -2\\ 0 & 0 & -2 & -3 & -4\\ 0 & 2 & 7 & 1 & -15\\ 0 & -1 & 0 & - 5 & 5\end(array)\kanan). $$
Langkah kedua
Kami meneruskan ke sifar elemen sepadan lajur kedua. Kami bersetuju untuk mengambil elemen baris kedua sebagai elemen penyelesaian, tetapi kami tidak dapat melakukan ini, kerana elemen yang diperlukan adalah sama dengan sifar. Kesimpulan: kami akan menukar baris. Baris pertama tidak boleh disentuh, kerana ia telah digunakan pada langkah pertama. Pilihannya tidak kaya: sama ada kita menukar baris kedua dan ketiga, atau kita menukar baris keempat dan kedua. Oleh kerana baris keempat mengandungi (-1), maka biarkan baris keempat mengambil bahagian dalam "pertukaran". Jadi, tukar baris kedua dan keempat:
$$ \kiri(\mulakan(susun)(cccc|c) 1 & 1/3 & 2/3 & 5/3 & -2\\ 0 & 0 & -2 & -3 & -4\\ 0 & 2 & 7 & 1 & -15\\ 0 & -1 & 0 & -5 & -5\end(array)\kanan)\rightarrow \left(\mula(array)(cccc|c) 1 & 1/3 & 2/3 & 5/3 & -2\\ 0 & -1 & 0 & -5 & -5\\ 0 & 2 & 7 & 1 & -15\\ 0 & 0 & -2 & -3 & -4 \end(array)\kanan) $$
Sekarang semuanya normal: elemen resolusi adalah sama dengan (-1). Ia berlaku, dengan cara itu, menukar kedudukan garis adalah mustahil, tetapi kita akan membincangkannya dalam contoh seterusnya No. 3. Buat masa ini, kami membahagikan baris kedua dengan (-1), dan kemudian menetapkan semula elemen lajur kedua. Sila ambil perhatian bahawa dalam lajur kedua, elemen yang terletak di baris keempat sudah sama dengan sifar, jadi kami tidak akan menyentuh baris keempat.
$$ \kiri(\mulakan(susun)(cccc|c) 1 & 1/3 & 2/3 & 5/3 & -2\\ 0 & -1 & 0 & -5 & -5\\ 0 & 2 & 7 & 1 & -15\\ 0 & 0 & -2 & -3 & -4\end(array)\kanan) \begin(array) (l) \phantom(0)\\II:(-1) \\\phantom(0)\\\phantom(0)\end(array) \rightarrow \left(\begin(array)(cccc|c) 1 & 1/3 & 2/3 & 5/3 & -2 \\ 0 & 1 & 0 & 5 & 5\\ 0 & 2 & 7 & 1 & -15\\ 0 & 0 & -2 & -3 & -4\end(array)\kanan) \begin(array) (l) I-1/3\cdot II\\ \phantom(0) \\III-2\cdot II\\\phantom(0)\end(array) \rightarrow\\ \rightarrow\left(\begin( tatasusunan)(cccc|c) 1 & 0 & 2/3 & 0 & -11/3\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & 7 & -9 & -25\\ 0 & 0 & -2 & -3 & -4\end(array)\kanan). $$
Langkah ketiga
Mari kita mula memproses lajur ketiga. Kami bersetuju untuk mengambil unsur pepenjuru matriks sistem sebagai elemen penyelesaian. Untuk langkah ketiga, ini bermakna memilih elemen yang terletak pada baris ketiga. Walau bagaimanapun, jika kita hanya mengambil elemen 7 sebagai elemen penyelesaian, maka keseluruhan baris ketiga perlu dibahagikan dengan 7. Nampaknya saya membahagi dengan (-2) adalah lebih mudah. Oleh itu, mari kita tukar baris ketiga dan keempat, dan kemudian elemen penyelesaian akan menjadi (-2):
$$ \kiri(\mulakan(susun)(cccc|c) 1 & 0 & 2/3 & 0 & -11/3\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & 7 & -9 & -25\\ 0 & 0 & -2 & -3 & -4\end(array)\kanan) \rightarrow \left(\mula(array)(cccc|c) 1 & 0 & 2/3 & 0 & -11/3\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & -2 & -3 & -4\\ 0 & 0 & 7 & -9 & -25\end(array)\kanan) $$
Elemen peleraian - (-2). Bahagikan baris ketiga dengan (-2) dan tetapkan semula elemen yang sepadan bagi lajur ketiga:
$$ \left(\begin(array)(cccc|c) 1 & 0 & 2/3 & 0 & -11/3\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & -2 & - 3 & -4\\ 0 & 0 & 7 & -9 & -25\end(array)\kanan) \begin(array) (l) \phantom(0)\\ \phantom(0) \\III:( -2)\\\phantom(0)\end(array)\rightarrow \left(\mula(array)(cccc|c) 1 & 0 & 2/3 & 0 & -11/3\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & 1 & 3/2 & 2\\ 0 & 0 & 7 & -9 & -25\end(array)\kanan) \mula(array) (l) I-2 /3\cdot III\\ \phantom(0) \\ \phantom(0)\\IV-7\cdot III\end(array)\rightarrow\\ \rightarrow\left(\begin(array)(cccc|c ) 1 & 0 & 0 & -1 & -5\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & 1 & 3/2 & 2\\ 0 & 0 & 0 & -39/2 & - 39\end(array)\kanan). $$
Langkah keempat
Mari kita teruskan ke sifar lajur keempat. Elemen penyelesaian terletak di baris keempat dan sama dengan nombor $-\frac(39)(2)$.
$$ \left(\begin(array)(cccc|c) 1 & 0 & 0 & -1 & -5\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & 1 & 3/2 & 2 \\ 0 & 0 & 0 & -39/2 & -39\end(array)\kanan) \begin(array) (l) \phantom(0)\\ \phantom(0) \\ \phantom(0) \\IV:\kiri(-\frac(39)(2)\kanan) \end(array)\rightarrow \left(\mula(array)(cccc|c) 1 & 0 & 0 & -1 & -5 \\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & 1 & 3/2 & 2\\ 0 & 0 & 0 & 1 & 2\end(array)\kanan) \begin(array) (l ) I+IV\\ II-5\cdot IV \\ III-3/2\cdot IV \\ \phantom(0) \end(array)\rightarrow\\ \rightarrow\left(\begin(array)(cccc |c) 1 & 0 & 0 & 0 & -3\\ 0 & 1 & 0 & 0 & -5\\ 0 & 0 & 1 & 0 & -1\\ 0 & 0 & 0 & 1 & 2\end (susun)\kanan). $$
Keputusan sudah berakhir. Jawapannya ialah: $x_1=-3$, $x_2=-5$, $x_3=-1$, $x_4=2$. Penyelesaian lengkap tanpa penjelasan:

Jawab: $x_1=-3$, $x_2=-5$, $x_3=-1$, $x_4=2$.
Contoh No. 3
Selesaikan SLAE $\left\(\mulakan(disejajarkan) & x_1-2x_2+3x_3+4x_5=-5;\\ & 2x_1+x_2+5x_3+2x_4+9x_5=-3;\\ & 3x_1+4x_2+7x_3+4x_4 +14x_5=-1;\\ & 2x_1-4x_2+6x_3+11x_5=2;\\ & -2x_1+14x_2-8x_3+4x_4-7x_5=20;\\ & -4x_1-7x_2-9x_3-6x_5-21x 9. \end(aligned)\right.$ dengan kaedah Gauss-Jordan Jika sistem tidak pasti, nyatakan penyelesaian asas.
Contoh yang sama dibincangkan dalam topik "Penyelesaian umum dan asas SLAE". Dalam bahagian kedua topik yang disebutkan contoh ini diselesaikan menggunakan kaedah Gaussian. Kami akan menyelesaikannya menggunakan kaedah Gauss-Jordan. Kami tidak akan memecahkan penyelesaian langkah demi langkah, kerana ini telah dilakukan dalam contoh sebelumnya.
$$ \kiri(\mulakan(susun)(ccccc|c) 1 & -2 & 3 & 0 & 4 & -5\\ 2 & 1 & 5 & 2 & 9 & -3\\ 3 & 4 & 7 & 4 & 14 & -1\\ 2 & -4 & 6 & 0 & 11 & 2\\ -2 & 14 & -8 & 4 & -7 & 20\\ -4 & -7 & -9 & -6 & -21 & -9 \end(array)\kanan) \begin(array) (l) \phantom(0) \\ II-2\cdot I\\ III-3\cdot I\\ IV-2\cdot I \\ V+2\cdot I\\VI+4\cdot I \end(array) \rightarrow \left(\begin(array)(ccccc|c) 1 & -2 & 3 & 0 & 4 & -5\ \\ 0 & 5 & -1 & 2 & 1 & 7\\ 0 & 10 & -2 & 4 & 2 & 14\\ 0 & 0 & 0 & 0 & 3 & 12\\ 0 & 10 & -2 & 4 & 1 & 10\\ 0 & -15 & 3 & -6 & -5 & -29 \end(array)\kanan) \begin(array) (l) \phantom(0) \\ II:5 \\ \ phantom(0)\\ \phantom(0)\\ \phantom(0) \\ \phantom(0)\end(array) \rightarrow \\ \left(\begin(array)(ccccc|c) 1 & - 2 & 3 & 0 & 4 & -5\\ 0 & 1 & -1/5 & 2/5 & 1/5 & 7/5\\ 0 & 10 & -2 & 4 & 2 & 14\\ 0 & 0 & 0 & 0 & 3 & 12\\ 0 & 10 & -2 & 4 & 1 & 10\\ 0 & -15 & 3 & -6 & -5 & -29 \end(array)\kanan) \ mulakan (tatasusunan) (l) I+2\cdot II \\ \phantom(0)\\ III-10\cdot II\\ IV:3\\ V-10\cdot II\\VI+15\cdot II \ tamat (tatasusunan) \rightarrow \left(\mulai(array)(ccccc|c) 1 & 0 & 13/5 & 4/5 & 22/5 & -11/5\\ 0 & 1 & -1/5 & 2 /5 & 1/5 & 7/5\\ 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 4\\ 0 & 0 & 0 & 0 & -1 & - 4\\ 0 & 0 & 0 & 0 & -2 & -8 \end(array)\kanan). $$
Saya percaya bahawa salah satu transformasi yang dibuat masih memerlukan penjelasan: $IV:3$. Semua elemen baris keempat boleh dibahagikan sepenuhnya dengan tiga, jadi semata-mata atas sebab pemudahan, kami membahagikan semua elemen baris ini kepada tiga. Baris ketiga dalam matriks berubah menjadi sifar. Mari kita memotong garis sifar:
$$ \kiri(\mulakan(susun)(ccccc|c) 1 & 0 & 13/5 & 4/5 & 22/5 & -11/5\\ 0 & 1 & -1/5 & 2/5 & 1/5 & 7/5\\ 0 & 0 & 0 & 0 & 1 & 4\\ 0 & 0 & 0 & 0 & -1 & -4\\ 0 & 0 & 0 & 0 & -2 & -8 \end(array)\kanan) $$
Sudah tiba masanya untuk kita beralih ke langkah ketiga, di mana unsur-unsur lajur ketiga harus ditetapkan semula. Walau bagaimanapun, unsur pepenjuru (baris ketiga) adalah sifar. Dan menukar kedudukan garisan tidak akan melakukan apa-apa. Kami telah menggunakan baris pertama dan kedua, jadi kami tidak boleh menyentuhnya. Tetapi tidak ada gunanya menyentuh baris keempat dan kelima, kerana masalah elemen resolusi sama dengan sifar tidak akan hilang.
Dalam keadaan ini, masalah boleh diselesaikan dengan cara yang sangat mudah. Kami tidak boleh mengendalikan lajur ketiga? Baiklah, mari kita beralih ke nombor empat. Mungkin dalam lajur keempat elemen baris ketiga tidak akan sama dengan sifar. Walau bagaimanapun, lajur keempat mengalami masalah yang sama seperti yang ketiga. Elemen baris ketiga dalam lajur keempat ialah sifar. Dan menukar tempat baris sekali lagi tidak akan memberikan apa-apa. Kami juga tidak boleh memproses lajur keempat? Baiklah, mari kita beralih ke nombor lima. Tetapi dalam lajur kelima, elemen baris ketiga bukan sifar. Ia sama dengan satu, yang cukup bagus. Jadi, elemen penyelesaian dalam lajur kelima adalah sama dengan 1. Elemen penyelesaian telah dipilih, jadi kami akan menjalankan transformasi selanjutnya kaedah Gauss-Jordan:
$$ \kiri(\mulakan(susun)(ccccc|c) 1 & 0 & 13/5 & 4/5 & 22/5 & -11/5\\ 0 & 1 & -1/5 & 2/5 & 1/5 & 7/5\\ 0 & 0 & 0 & 0 & 1 & 4\\ 0 & 0 & 0 & 0 & -1 & -4\\ 0 & 0 & 0 & 0 & -2 & -8 \end(array)\kanan) \begin(array) (l) I-22/5\cdot III \\ II-1/5\cdot III \\ \phantom(0)\\ IV+III\\ V+ 2 \cdot III \end(array) \rightarrow \left(\begin(array)(ccccc|c) 1 & 0 & 13/5 & 4/5 & 0 & -99/5\\ 0 & 1 & -1 / 5 & 2/5 & 0 & 3/5\\ 0 & 0 & 0 & 0 & 1 & 4\\ 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 \end(array)\kanan) \rightarrow \\ \rightarrow\left|\text(Mengalih keluar garisan sifar)\kanan|\rightarrow \left(\mulakan(array)(ccccc|c) 1 & 0 & 13/5 & 4/5 & 0 & -99/5\\ 0 & 1 & -1/5 & 2/5 & 0 & 3/5\\ 0 & 0 & 0 & 0 & 1 & 4 \end(array)\ kanan )$$
Kami telah mengurangkan matriks sistem dan matriks sistem lanjutan kepada bentuk berperingkat. Kedudukan kedua-dua matriks adalah sama dengan $r=3$, i.e. anda perlu memilih 3 pembolehubah asas. Bilangan yang tidak diketahui ialah $n=5$, jadi kita perlu memilih $n-r=2$ pembolehubah bebas. Sejak $r< n$, то согласно следствию из теоремы Кронекера-Капелли sistem ini tidak pasti (iaitu mempunyai bilangan penyelesaian yang tidak terhingga). Untuk mencari penyelesaian kepada sistem, kami membuat "langkah":

Pada "langkah" terdapat elemen dari lajur No. 1, No. 2, No. 5. Akibatnya, pembolehubah asas ialah $x_1$, $x_2$, $x_5$. Pembolehubah bebas, masing-masing, ialah $x_3$, $x_4$. Kami akan memindahkan lajur No. 3 dan No. 4, sepadan dengan pembolehubah bebas, di luar garisan, sementara, sudah tentu, tidak lupa untuk menukar tanda-tanda mereka.
$$ \kiri(\mulakan(susun)(ccccc|c) 1 & 0 & 13/5 & 4/5 & 0 & -99/5\\ 0 & 1 & -1/5 & 2/5 & 0 & 3/5\\ 0 & 0 & 0 & 0 & 1 & 4 \end(array)\kanan)\rightarrow \left(\mula(array)(ccc|ccc) 1 & 0 & 0 & -99/5 & -13/5 & -4/5\\ 0 & 1 & 0 & 3/5 & 1/5 & -2/5\\ 0 & 0 & 1 & 4 & 0 & 0\end(array)\kanan) . $$
Daripada matriks terakhir kita memperoleh penyelesaian umum: $\left\(\begin(aligned) & x_1=-\frac(99)(5)-\frac(13)(5)x_3-\frac(4)(5 )x_4; \\ & x_2=\frac(3)(5)+\frac(1)(5)x_3-\frac(2)(5)x_4;\\ & x_3 \in R;\\ & x_4\ dalam R; \\ & x_5=4. \end(aligned)\right.$ Kami mencari penyelesaian asas dengan mengambil pembolehubah bebas sama dengan sifar, iaitu $x_3=0$, $x_4=0$:
$$ \kiri\(\mulakan(diselaraskan) & x_1=-\frac(99)(5);\\ & x_2=\frac(3)(5);\\ & x_3=0;\\ & x_4= 0;\\ & x_5=4.\end(aligned)\kanan.$$
Masalah selesai, yang tinggal hanyalah menulis jawapan.
Jawab: Keputusan bersama: $\left\(\begin(aligned) & x_1=-\frac(99)(5)-\frac(13)(5)x_3-\frac(4)(5)x_4;\\ & x_2=\ frac(3)(5)+\frac(1)(5)x_3-\frac(2)(5)x_4;\\ & x_3 \in R;\\ & x_4\in R;\\ & x_5=4 .\end(aligned)\right.$, penyelesaian asas: $\left\(\begin(aligned) & x_1=-\frac(99)(5);\\ & x_2=\frac(3)(5) ;\\ & x_3=0;\\ & x_4=0;\\ & x_5=4. \end(diselaraskan)\kanan.$.
Pada kaedah grafik untuk menyelesaikan masalah LP, kami sebenarnya memilih daripada set bucu kepunyaan sempadan set penyelesaian kepada sistem ketaksamaan satu bucu di mana nilai fungsi objektif mencapai maksimum (minimum). Dalam kes dua pembolehubah, kaedah ini intuitif sepenuhnya dan membolehkan anda mencari penyelesaian kepada masalah dengan cepat.
Jika terdapat tiga atau lebih pembolehubah dalam masalah, dan dalam sebenar tugas ekonomi Hanya situasi sedemikian, sukar untuk menggambarkan kawasan penyelesaian sistem kekangan. Masalah sedemikian diselesaikan menggunakan kaedah simplex atau dengan kaedah penambahbaikan berturut-turut. Idea kaedah ini mudah dan adalah seperti berikut.
Mengikut peraturan tertentu, pelan rujukan awal (beberapa puncak kawasan kekangan) ditemui. Ia menyemak sama ada rancangan itu optimum. Jika ya, maka masalah itu selesai. Jika tidak, maka kita beralih kepada rancangan yang lebih baik - ke puncak yang lain. nilai fungsi objektif pada satah ini (di puncak ini) jelas lebih baik daripada yang sebelumnya. Algoritma peralihan dijalankan menggunakan langkah pengiraan tertentu, yang ditulis dengan mudah dalam bentuk jadual yang dipanggil jadual simplex . Oleh kerana terdapat bilangan bucu yang terhingga, dalam bilangan langkah yang terhingga kita sampai pada penyelesaian yang optimum.
Mari kita pertimbangkan kaedah simplex pada contoh khusus tugas tentang merangka rancangan.
Mari kita perhatikan sekali lagi bahawa kaedah simpleks boleh digunakan untuk menyelesaikan masalah kanonik LP dikurangkan kepada bentuk khas, iaitu, mempunyai asas, sisi kanan positif dan fungsi objektif yang dinyatakan dalam sebutan pembolehubah bukan asas. Sekiranya masalah itu tidak dikurangkan kepada bentuk khas, maka anda perlukan langkah tambahan, yang akan kita bincangkan kemudian.
Mari kita pertimbangkan masalah rancangan pengeluaran, setelah membina model sebelum ini dan membawanya ke bentuk khas.
Tugasan.
Untuk pembuatan produk A Dan DALAM Gudang boleh mengeluarkan tidak lebih daripada 80 unit bahan mentah. Lebih-lebih lagi, untuk pembuatan produk A dua unit digunakan, dan produk DALAM- satu unit bahan mentah. Adalah perlu untuk merancang pengeluaran supaya keuntungan yang paling besar dipastikan jika produk A ia diperlukan untuk menghasilkan tidak lebih daripada 50 keping, dan produk DALAM- tidak lebih daripada 40 pcs. Lebih-lebih lagi, keuntungan daripada penjualan satu produk A- 5 rubel, dan dari DALAM- 3 gosok.
Jom bina model matematik, menandakan sebagai X 1 kuantiti produk A dalam pelan, untuk X 2 - bilangan produk DALAM. maka sistem kekangan akan kelihatan seperti ini:
Mari kita bawa masalah kepada bentuk kanonik dengan memperkenalkan pembolehubah tambahan:
 (3.10)
(3.10)
F = -5x 1 - 3x 2 → min.
Tugasan ini mempunyai jenis khas(dengan asas, bahagian sebelah kanan adalah bukan negatif). Ia boleh diselesaikan menggunakan kaedah simpleks.
sayapentas. Merekod masalah dalam jadual simplex. Terdapat kesesuaian satu dengan satu antara sistem kekangan masalah (3.10) dan jadual simpleks. Terdapat seberapa banyak baris dalam jadual kerana terdapat kesamaan dalam sistem kekangan, dan terdapat banyak lajur kerana terdapat pembolehubah bebas. Pembolehubah asas mengisi lajur pertama, yang percuma - baris atas meja. Pokoknya dipanggil indeks, pekali pembolehubah dalam fungsi objektif ditulis di dalamnya. Di sudut kanan bawah, 0 pada mulanya ditulis jika tiada ahli bebas dalam fungsi; jika ada, maka tulis dengan tanda yang bertentangan. Di tempat ini (di sudut kanan bawah) akan terdapat nilai fungsi objektif, yang sepatutnya meningkat dalam nilai mutlak apabila bergerak dari satu jadual ke jadual lain. Jadi, Jadual 3.4 sepadan dengan sistem sekatan kami, dan kami boleh meneruskan ke peringkat II penyelesaian.
Jadual 3.4
|
asas |
percuma |
||
IIpentas. Menyemak pelan rujukan untuk optimum.
Jadual 3.4 ini sepadan dengan pelan rujukan berikut:
(X 1 , X 2 , X 3 , X 4 , X 5) = (0, 0, 50, 40, 80).
Pembolehubah bebas X 1 , X 2 sama dengan 0; X 1 = 0, X 2 = 0. Dan pembolehubah asas X 3 , X 4 , X 5 mengambil nilai X 3 = 50, X 4 = 40, X 5 = 80 - daripada lajur syarat percuma. Nilai fungsi objektif:
-F = - 5X 1 - 3X 2 = -5 0 - 3 0 = 0.
Tugas kami adalah untuk menyemak sama ada pelan rujukan yang diberikan adalah optimum. Untuk melakukan ini, anda perlu melihat garis indeks - garis fungsi sasaran F.
Pelbagai situasi boleh berlaku.
1. Dalam indeks F- tiada unsur negatif dalam rentetan. Ini bermakna rancangan itu adalah optimum, dan penyelesaian kepada masalah itu boleh ditulis. Fungsi objektif mencapai matlamatnya nilai optimum, sama dengan nombor di sudut kanan bawah, diambil dengan tanda bertentangan. Mari kita beralih ke peringkat IV.
2. Baris indeks mempunyai sekurang-kurangnya satu elemen negatif yang lajurnya tidak mempunyai unsur positif. Kemudian kita membuat kesimpulan bahawa fungsi objektif F→∞ berkurangan tanpa had.
3. Baris indeks mempunyai unsur negatif yang mempunyai sekurang-kurangnya satu unsur positif dalam lajurnya. Kemudian kita meneruskan ke peringkat III seterusnya. Kami mengira semula jadual, menambah baik pelan rujukan.
IIIpentas. Penambahbaikan pelan rujukan.
Daripada unsur negatif indeks F-baris, pilih yang mempunyai modulus terbesar, panggil penyelesaian lajur yang sepadan dan tandakannya dengan "".
Untuk memilih baris penyelesaian, adalah perlu untuk mengira nisbah unsur-unsur lajur istilah bebas sahaja Kepada positif elemen lajur resolusi. Pilih yang minimum daripada hubungan yang diperolehi. Elemen yang sepadan di mana minimum dicapai dipanggil menyelesaikan. Kami akan menyerlahkannya dengan segi empat sama.
Dalam contoh kita, ![]() , elemen 2 adalah permisif. Garis yang sepadan dengan elemen ini juga dipanggil menyelesaikan (Jadual 3.5).
, elemen 2 adalah permisif. Garis yang sepadan dengan elemen ini juga dipanggil menyelesaikan (Jadual 3.5).
Jadual 3.5

Setelah memilih elemen yang membenarkan, kami mengira semula jadual mengikut peraturan:
1. Dalam jadual baharu dengan saiz yang sama seperti sebelumnya, pembolehubah baris dan lajur penyelesaian ditukar, yang sepadan dengan peralihan kepada asas baharu. Dalam contoh kami: X 1 dimasukkan dalam asas, sebaliknya X 5, yang meninggalkan asas dan kini percuma (Jadual 3.6).
Jadual 3.6
|
asas |
percuma |
||
2. Sebagai ganti unsur penyelesaian 2, tulis nombor songsangnya.
3. Kami membahagikan elemen garis resolusi dengan elemen resolusi.
4. Kami membahagikan elemen lajur resolusi dengan elemen resolusi dan menulisnya dengan tanda bertentangan.
5. Untuk mengisi baki elemen jadual 3.6, kami mengira semula menggunakan peraturan segi empat tepat. Katakan kita mahu mengira elemen pada kedudukan 50.
Kami menghubungkan unsur ini secara mental dengan yang menyelesaikan, cari hasil, tolak hasil darab unsur yang terletak pada pepenjuru lain dari segi empat tepat yang terhasil. Kami membahagikan perbezaan dengan elemen penyelesaian.
Jadi, . Kami menulis 10 di tempat yang terdapat 50. Begitu juga :
, ![]() , ,
, , ![]() .
.
Jadual 3.7

Kami ada meja baru 3.7, pembolehubah asas kini ialah pembolehubah (x 3,x 4,x 1). Nilai fungsi objektif menjadi sama dengan -200, iaitu menurun. Untuk menyemak penyelesaian asas ini untuk optimum, kita mesti pergi lagi ke peringkat II. Proses ini jelas terhingga; kriteria berhenti ialah mata 1 dan 2 peringkat II.
Mari selesaikan penyelesaian masalah. Untuk melakukan ini, mari kita semak garis indeks dan, melihat elemen negatif di dalamnya, panggil penyelesaian lajur yang sepadan dan, mengikut peringkat III, kira semula jadual. Setelah menyusun hubungan dan memilih minimum = 40 di antaranya, kami menentukan elemen penyelesaian 1. Sekarang kami menjalankan pengiraan semula mengikut peraturan 2-5.
Jadual 3.8
|
asas |
percuma |
||
|
x 3 = 30, X 2 = 40, X 1 = 20. Pembolehubah bebas ialah 0, X 5 = 0, X 4 = 0. Fungsi objektif mengambil nilai elemen terakhir lajur sebutan bebas dengan tanda bertentangan: - F = -220 F = 220, dalam contoh kami fungsi itu diperiksa pada min, dan pada mulanya F maks, jadi tanda itu sebenarnya berubah dua kali. Jadi, X* = (20, 40, 30, 0, 0), F* = 220. Jawapan kepada masalah: Ia perlu memasukkan 20 produk jenis dalam rancangan pengeluaran A, 40 produk jenis B, manakala keuntungan akan maksimum dan akan bersamaan dengan 220 rubel. Pada penghujung bahagian ini, kami membentangkan carta alir algoritma kaedah simpleks, yang betul-betul mengulangi langkah-langkah, tetapi mungkin bagi sesetengah pembaca ia akan lebih mudah digunakan, kerana anak panah menunjukkan arah tindakan yang jelas. Pautan di atas kotak dalam carta alir menunjukkan peringkat atau sub-titik mana kumpulan transformasi yang sepadan tergolong. peraturan untuk mencari pelan rujukan awal akan dirumuskan dalam perenggan 3.7.
Soalan untuk mengawal diri 1. Bagaimanakah jadual simpleks dibina? 2. Bagaimanakah perubahan dalam asas ditunjukkan dalam jadual? 3. Rumuskan kriteria penghentian bagi kaedah simpleks. 4. Bagaimana untuk mengatur pengiraan semula jadual? 5. Dari baris mana yang sesuai untuk mula mengira semula jadual? |