Множественная регрессия не является результатом преобразования уравнения:

-
;

-
.

Линеаризация подразумевает процедуру …

- приведения уравнения множественной регрессии к парной;

+ приведения нелинейного уравнения к линейному виду;

- приведения линейного уравнения к нелинейному виду;

- приведения нелинейного уравнения относительно параметров к уравнению, линейному относительно результата.

Остатки не изменяются;

Уменьшается количество наблюдений

В стандартизованном уравнении множественной регрессии переменными являются:

Исходные переменные;

Стандартизованные параметры;

Средние значения исходных переменных;

Стандартизованные переменные.

Одним из методов присвоения числовых значений фиктивным переменным является. . .

+– ранжирование;

Выравнивание числовых значений по возрастанию;

Выравнивание числовых значений по убыванию;

Нахождение среднего значения.

В матрице парных коэффициентов корреляции отображены значения парных коэффициентов линейной корреляции между. . . .

Переменными;

Параметрами;

Параметрами и переменными;

Переменными и случайными факторами.

Метод оценки параметров моделей с гетероскедастичными остатками называется ____________ методом наименьших квадратов:

Обычным;

Косвенным;

Обобщенным;

Минимальным.

Дано уравнение регрессии . Определите спецификацию модели.

Полиномиальное уравнение парной регрессии;

Линейное уравнение простой регрессии;

Полиномиальное уравнение множественной регрессии;

Линейное уравнение множественной регрессии.

В стандартизованном уравнении свободный член ….

Равен 1;

Равен коэффициенту множественной детерминации;

Равен коэффициенту множественной корреляции;

Отсутствует.

В качестве фиктивных переменных в модель множественной регрессии включаются факторы,

Имеющие вероятностные значения;

Имеющие количественные значения;

Не имеющие качественных значений;

Не имеющие количественных значений.

Факторы эконометрической модели являются коллинеарными, если коэффициент …

Корреляции между ними по модулю больше 0,7;

Детерминации между ними по модулю больше 0,7;

Детерминации между ними по модулю меньше 0,7;

Обобщенный метод наименьших квадратов отличается от обычного МНК тем, что при применении ОМНК …

Преобразуются исходные уровни переменных;

Остатки не изменяются;

Остатки приравниваются к нулю;

Уменьшается количество наблюдений.

Объем выборки определяется …

Числовыми значением переменных, отбираемых в выборку;

Объемом генеральной совокупности;

Числом параметров при независимых переменных;

Числом результативных переменных.

11. Множественная регрессия не является результатом преобразования уравнения:

+-
;

-
;

-
.

Исходные значения фиктивных переменных предполагают значения …

Качественные;

Количественно измеримые;

Одинаковые;

Значения.

Обобщенный метод наименьших квадратов подразумевает …

Преобразование переменных;

Переход от множественной регрессии к парной;

Линеаризацию уравнения регрессии;

Двухэтапное применение метода наименьших квадратов.

Линейное уравнение множественной регрессии имеет вид . Определите какой из факторовили:

+- , так как 3,7>2,5;

Оказывают одинаковое влияние;

- , так как 2,5>-3,7;

По этому уравнению нельзя ответить на поставленный вопрос, так как коэффициенты регрессии несравнимы между собой.

Включение фактора в модель целесообразно, если коэффициент регрессии при этом факторе является …

Нулевым;

Незначимым;

Существенным;

Несущественным.

Что преобразуется при применении обобщенного метода наименьших квадратов?

Стандартизованные коэффициенты регрессии;

Дисперсия результативного признака;

Исходные уровни переменных;

Дисперсия факторного признака.

Проводится исследование зависимости выработки работника предприятия от ряда факторов. Примером фиктивной переменной в данной модели будет являться ______ работника.

Возраст;

Уровень образования;

Заработная плата.

Переход от точечного оценивания к интервальному возможен, если оценки являются:

Эффективными и несостоятельными;

Неэффективными и состоятельными;

Эффективными и несмещенными;

Состоятельными и смещенными.

Матрица парных коэффициентов корреляции строится для выявления коллинеарных и мультиколлинеарных …

Параметров;

Случайных факторов;

Существенных факторов;

Результатов.

На основании преобразования переменных при помощи обобщенного метода наименьших квадратов получаем новое уравнение регрессии, которое представляет собой:

Взвешенную регрессию, в которой переменные взяты с весами
;

;

Нелинейную регрессию, в которой переменные взяты с весами
;

Взвешенную регрессию, в которой переменные взяты с весами .

Если расчетное значение критерия Фишера меньше табличного значения, то гипотеза о статистической незначимости уравнения …

Отвергается;

Незначима;

Принимается;

Несущественна.

Если факторы входят в модель как произведение, то модель называется:

Суммарной;

Производной;

Аддитивной;

Мультипликативной.

Уравнение регрессии, которое связывает результирующий признак с одним из факторов при зафиксированных на среднем уровне значении других переменных, называется:

Множественным;

Существенным;

Частным;

Несущественным.

Относительно количества факторов, включенных в уравнение регрессии, различают …

Линейную и нелинейную регрессии;

Непосредственную и косвенную регрессии;

Простую и множественную регрессию;

Множественную и многофакторную регрессию.

Требованием к уравнениям регрессии, параметры которых можно найти при помощи МНК является:

Равенство нулю значений факторного признака4

Нелинейность параметров;

Равенство нулю средних значений результативной переменной;

Линейность параметров.

Метод наименьших квадратов не применим для …

Линейных уравнений парной регрессии;

Полиномиальных уравнений множественной регрессии;

Уравнений, нелинейных по оцениваемым параметрам;

Линейных уравнений множественной регрессии.

При включении фиктивных переменных в модель им присваиваются …

Нулевые значения;

Числовые метки;

Одинаковые значения;

Качественные метки.

Если между экономическими показателями существует нелинейная связь, то …

Нецелесообразно использовать спецификацию нелинейного уравнения регрессии;

Целесообразно использовать спецификацию нелинейного уравнения регрессии;

Целесообразно использовать спецификацию линейного уравнение парной регрессии;

Необходимо включить в модель другие факторы и использовать линейное уравнение множественной регрессии.

Результатом линеаризации полиномиальных уравнений является …

Нелинейные уравнения парной регрессии;

Линейные уравнения парной регрессии;

Нелинейные уравнения множественной регрессии;

Линейные уравнения множественной регрессии.

В стандартизованном уравнении множественной регрессии
0,3;
-2,1. Определите, какой из факторовилиоказывает более сильное влияние на:

+- , так как 2,1>0,3;

По этому уравнению нельзя ответить на поставленный вопрос, так как неизвестны значения «чистых» коэффициентов регрессии;

- , так как 0,3>-2,1;

По этому уравнению нельзя ответить на поставленный вопрос, так как стандартизированные коэффициенты несравнимы между собой.

Факторные переменные уравнения множественной регрессии, преобразованные из качественных в количественные называются …

Аномальными;

Множественными;

Парными;

Фиктивными.

Оценки параметров линейного уравнения множественной регрессии можно найти при помощи метода:

Средних квадратов;

Наибольших квадратов;

Нормальных квадратов;

Наименьших квадратов.

Основным требованием к факторам, включаемым в модель множественной регрессии, является:

Отсутствие взаимосвязи между результатом и фактором;

Отсутствие взаимосвязи между факторами;

Отсутствие линейной взаимосвязи между факторами;

Наличие тесной взаимосвязи между факторами.

Фиктивные переменные включаются в уравнение множественной регрессии для учета действия на результат признаков …

Качественного характера;

Количественного характера;

Несущественного характера;

Случайного характера.

Из пары коллинеарных факторов в эконометрическую модель включается тот фактор,

Который при достаточно тесной связи с результатом имеет наибольшую связь с другими факторами;

Который при отсутствии связи с результатом имеет максимальную связь с другими факторами;

Который при отсутствии связи с результатом имеет наименьшую связь с другими факторами;

Который при достаточно тесной связи с результатом имеет меньшую связь с другими факторами.

Гетероскедастичность подразумевает …

Постоянство дисперсии остатков независимо от значения фактора;

Зависимость математического ожидания остатков от значения фактора;

Зависимость дисперсии остатков от значения фактора;

Независимость математического ожидания остатков от значения фактора.

Величина остаточной дисперсии при включении существенного фактора в модель:

Не изменится;

Будет увеличиваться;

Будет равно нулю;

Будет уменьшаться.

Если спецификация модели отображает нелинейную форму зависимости между экономическими показателями, то нелинейно уравнение …

Регрессии;

Детерминации;

Корреляции;

Аппроксимации.

Исследуется зависимость, которая характеризуется линейным уравнением множественной регрессии. Для уравнения рассчитано значение тесноты связи результативной переменной с набором факторов. В качестве этого показателя был использован множественный коэффициент …

Корреляции;

Эластичности;

Регрессии;

Детерминации.

Строится модель зависимости спроса от ряда факторов. Фиктивной переменной в данном уравнении множественной регрессии не является _________потребителя.

Семейное положение;

Уровень образования;

Для существенного параметра расчетное значение критерия Стьюдента …

Больше табличного значения критерия;

Равно нулю;

Не больше табличного значения критерия Стьюдента;

Меньше табличного значения критерия.

Систему МНК, построенную для оценки параметров линейного уравнения множественной регрессии можно решить …

Методом скользящего среднего;

Методом определителей;

Методом первых разностей;

Симплекс-методом.

Показатель, характеризующий на сколько сигм изменится в среднем результат при изменении соответствующего фактора на одну сигму, при неизменном уровне других факторов, называется ____________коэффициентом регрессии

Стандартизованным;

Нормализованным;

Выровненным;

Центрированным.

Мультиколлинеарность факторов эконометрической модели подразумевает …

Наличие нелинейной зависимости между двумя факторами;

Наличие линейной зависимости между более чем двумя факторами;

Отсутствие зависимости между факторами;

Наличие линейной зависимости между двумя факторами.

Обобщенный метод наименьших квадратов не используется для моделей с _______ остатками.

Автокоррелированными и гетероскедастичными;

Гомоскедастичными;

Гетероскедастичными;

Автокоррелированными.

Методом присвоения числовых значений фиктивным переменным не является:

Ранжирование;

Присвоение цифровых меток;

Нахождения среднего значения;

Присвоение количественных значений.

Нормально распределенных остатков;

Гомоскедастичных остатков;

Автокорреляции остатков;

Автокорреляции результативного признака.

Отбор факторов в модель множественной регрессии при помощи метода включения основан на сравнении значений …

Общей дисперсии до и после включения фактора в модель;

Остаточной дисперсии до и после включения случайных факторов в модель;

Дисперсии до и после включения результата в модель;

Остаточной дисперсии до и после включения фактора модель.

Обобщенный метод наименьших квадратов используется для корректировки …

Параметров нелинейного уравнения регрессии;

Точности определения коэффициента множественной корреляции;

Автокорреляции между независимыми переменными;

Гетероскедастичности остатков в уравнении регрессии.

После применения обобщенного метода наименьших квадратов удается избежать_________ остатков

Гетероскедастичности;

Нормального распределения;

Равенства нулю суммы;

Случайного характера.

Фиктивные переменные включаются в уравнения ____________регрессии

Случайной;

Парной;

Косвенной;

Множественной.

Взаимодействие факторов эконометрической модели означает, что …

Влияние факторов на результирующий признак зависит от значений другого неколлинеарного им фактора;

Влияние факторов на результирующий признак усиливается, начиная с определенного уровня значений факторов;

Факторы дублируют влияние друг друга на результат;

Влияние одного из факторов на результирующий признак не зависит от значений другого фактора.

Тема Множественная регрессия (Задачи)

Уравнение регрессии, построенное по 15 наблюдениям, имеет вид:

Пропущенные значения, а также доверительный интервал для

с вероятностью 0,99 равны:

Уравнение регрессии, построенное по 20 наблюдениям, имеет вид:

с вероятностью 0,9 равны:

Уравнение регрессии, построенное по 16 наблюдениям, имеет вид:

Пропущенные значения, а также доверительный интервал для с вероятностью 0,99 равны:

Уравнение регрессии в стандартизированном виде имеет вид:

Частные коэффициенты эластичности равны:

Стандартизованное уравнение регрессии имеет вид:

Частные коэффициенты эластичности равны:

Стандартизованное уравнение регрессии имеет вид:

Частные коэффициенты эластичности равны:

Стандартизованное уравнение регрессии имеет вид:

Частные коэффициенты эластичности равны:

Стандартизованное уравнение регрессии имеет вид:

Частные коэффициенты эластичности равны:

По 18 наблюдениям получены следующие данные:

;
;
;
;

равны:

По 17 наблюдениям получены следующие данные:

;
;
;
;

Значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра равны:

По 22 наблюдениям получены следующие данные:

;
;
;
;

Значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра равны:

По 25 наблюдениям получены следующие данные:

;
;
;
;

Значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра равны:

По 24 наблюдениям получены следующие данные:

;
;
;
;

Значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра равны:

По 28 наблюдениям получены следующие данные:

;
;
;
;

Значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра равны:

По 26 наблюдениям получены следующие данные:

;
;
;
;

Значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра равны:

В уравнении регрессии:

Восстановить пропущенные характеристики; построить доверительный интервал для с вероятностью 0,95, еслиn=12

Эта процедура описывает, как определить переменную пакета, в которой хранится информация состояния CDC.

Переменная состояния CDC загружается, инициализируется и обновляется с помощью задачи «Управление CDC» и используется компонентом потока данных «Источник CDC» в целях определения текущего диапазона обработки для записей с данными об изменениях. Переменная состояния CDC может быть определена в контейнере, который является общим для задачи «Управление CDC» и источника CDC. Такое определение может быть сделано на уровне пакета, а также в других контейнерах, таких как контейнер цикла.

Изменять вручную значение переменной состояния CDC не рекомендуется, но выполнение этой операции может оказаться полезным для ознакомления с содержимым переменной.

В следующей таблице приведено общее описание компонентов значения переменной состояния CDC.

Компонент	Description
	Это имя текущего состояния CDC.
CS	Это обозначает точку начала текущего диапазона обработки (Current Start).
	Это последний регистрационный номер транзакции в журнале, обработанный во время предыдущего запуска CDC.
CE	Это обозначает конечную точку текущего диапазона обработки (Current End). Наличие компонента CE в состоянии CDC указывает на то, что пакет CDC обрабатывается в данный момент или что произошел сбой пакета CDC до полного завершения обработки всего диапазона CDC.
	Это последний номер LSN, который должен быть обработан во время текущего выполнения CDC. Всегда предполагается, что последний последовательный номер, который должен быть обработан, является максимальным (0xFFF…).
IR	Это обозначает начальный диапазон обработки.
	Это номер LSN изменения прямо перед началом первоначальной загрузки.
	Это номер LSN изменения непосредственно после завершения первоначальной загрузки.
TS	Это обозначает отметку времени последнего обновления состояния CDC.
>	Это десятичное представление 64-разрядного свойства System.DateTime.UtcNow.
ER	Оно отображается в случае сбоя последней операции и содержит краткое описание причины ошибки. При наличии этого компонента он всегда отображается последним.
	Это краткое описание ошибки.

Номера LSN и последовательные номера кодируются в виде шестнадцатеричной строки длиной до 20 знаков, представляющей значение LSN Binary(10).

В следующей таблице описаны возможные значения состояния CDC.

Состояние	Description
(INITIAL)	Это исходное состояние до выполнения какого-либо пакета в текущей группе CDC. Это состояние также имеет место, если состояние CDC пусто.
ILSTART (запуск начальной загрузки)	Это состояние, когда запускается начальная загрузка пакета после вызова задачи «Управление CDC» операцией MarkInitialLoadStart .
ILEND (завершение начальной загрузки)	Это состояние, когда начальная загрузка пакета успешно завершается после вызова задачи «Управление CDC» операцией MarkInitialLoadEnd .
ILUPDATE (обновление начальной загрузки)	Это состояние после выполнения пакета обновления тонкого канала после начальной загрузки во время продолжения обработки диапазона начальной обработки. Это происходит после вызова задачи «Управление CDC» операцией GetProcessingRange .
TFEND (завершение обновления тонкого канала)	Это состояние, ожидаемое для регулярного выполнения CDC. Оно показывает, что предыдущее выполнение завершилось успешно и можно начинать новое выполнение с новым диапазоном обработки.
TFSTART	Это состояние, которое возникает при последующем выполнении пакета обновления тонкого канала после вызова задачи "Управление CDC" операцией GetProcessingRange . Оно показывает, что регулярное выполнение CDC начато, но еще не завершено или завершено неверно (MarkProcessedRange ).
TFREDO (повторная обработка обновления тонкого канала)	Это состояние операции GetProcessingRange , наступающее после TFSTART. Оно показывает, что предыдущее выполнение не завершилось успешно. Если используется столбец __$reprocessing, он получает значение 1, чтобы показать, что пакет может повторно обрабатывать строки, уже находящиеся в целевой базе данных.
ERROR	Группа CDC находится в состоянии ERROR.

Ниже приведены примеры значений переменной состояния CDC.

ILSTART/IR/0x0000162B158700000000//TS/2011-08-07T17:10:43.0031645/

TFEND/CS/0x0000025B000001BC0003/TS/2011-07-17T12:05:58.1001145/

TFSTART/CS/0x0000030D000000AE0003/CE/0x0000159D1E0F01000000/TS/2011-08-09T05:30:43.9344900/

TFREDO/CS/0x0000030D000000AE0003/CE/0x0000159D1E0F01000000/TS/2011-08-09T05:30:59.5544900/

Определение переменной состояния CDC

В SQL Server Data Toolsоткройте пакет SQL Server 2016 Integration Services (SSIS) , в котором имеется поток CDC, где необходимо определить переменную.

Щелкните вкладку Обозреватель пакетов и добавьте новую переменную.

Присвойте переменной имя, которое поможет обозначить ее как переменную состояния.

Назначьте переменной тип данных String .

Не присваивайте переменной значение в составе ее определения. Значение должно быть задано задачей «Управление CDC».

Если намечено использовать задачу «Управление CDC» с параметром Автоматическое сохранение состояния , то переменная состояния CDC будет считываться из указанной таблицы состояния в базе данных и после обновления снова записываться в ту же таблицу при изменении ее значения. Дополнительные сведения о таблице состояния см. в разделах и .

Если не используется задача «Управление CDC» с параметром автоматического сохранения состояния, то необходимо загружать значение переменной из постоянного хранилища, в котором это значение было сохранено в последний раз при прогоне пакета, а затем снова записывать его в постоянное хранилище после завершения работы с текущим диапазоном обработки.

Основы > Теоретические основы электротехники

Метод переменных состояния
Уравнениями состояния можно назвать любую систему уравнений, определяющих режим цепи. В более узком смысле - это система дифференциальных уравнений первого порядка, разрешенная относительно производных.
Методом переменных состояния назовем анализ цепи, основанный на решении уравнений состояния (первого порядка), записанных в форме Коши. Таким образом, метод переменных состояния - один из методов расчета прежде всего переходных процессов. Далее предполагается, что цепь имеет только независимые источники и не содержит индуктивных сечений и емкостных контуров. В противном случае составление уравнений становится намного сложнее.
Для линейной цепи с постоянными сосредоточенными параметрами ток каждой ветви, напряжение между выбранными выводами, заряд на обкладках конденсатора и т. д. всегда можно найти как решение составленного для этого тока, напряжения, заряда и т. д. дифференциального уравнения (например, исключением других токов и напряжений из системы уравнений Кирхгофа):

Введением переменных это уравнение сводится к эквивалентной системе дифференциальных уравнений первого порядка:

Здесь переменными, которые называются переменными состояния , служат переменная х и ее производные.
Как известно, переходный процесс в любой цепи, кроме ее параметров (значений r , L, С, М) и действующих источников [ e(t) и J(t)], определяется независимыми начальными (t = 0) условиями - токами в индуктивных элементах и напряжениями на емкостных элементах , которые должны быть известны или рассчитаны. Через них выражаются искомые величины во время переходного процесса. Они же определяют энергетическое состояние цепи. Поэтому в качестве переменных состояния целесообразно выбирать токи и напряжения . Действующие источники можно назвать входными величинами , искомые величины - выходными . Для цепи с n независимыми токами и напряжениями должны быть заданы еще n независимых начальных условий.

Сокращенно дифференциальные уравнения состояния запишем в матричной форме так:

или короче

где X матрица-столбец (размера n x 1) переменных состояния (вектор переменных состояния); F - матрица-столбец (размера m x 1) ЭДС и токов источников (внешних возмущений); А - квадратная матрица порядка n (основная); В - матрица размера п х m (матрица связи). Элементы этих матриц определяются топологией и параметрами цепи.
Для выходных величин (если определяются не токи в индуктивных и напряжения на емкостных элементах) в матричной форме система алгебраических уравнений имеет вид

или короче

где W - матрица-столбец (размера l x 1 ); M - матрица связи (размера l x n ); N - матрица связи (размера l x m ).
Элементы матриц зависят от топологии и параметров цепи. Для уравнений состояния разработаны и машинные алгоритмы формирования на основе топологии и значений параметров.
Уравнения в матричной форме (14.91) можно составить, например, с применением метода наложения. Для получения зависимостей между производными переменных состояния, т. е. и переменными состояния , а также ЭДС и токами источников, действующими в цепи, будем считать, что переменные состояния заданы. Рассматриваемую цепь, например на рис. 14.41, а, заменим после коммутации эквивалентной (рис. 14.41,6), у которой каждый заданный ток представлен источником тока , а каждое заданное напряжение - источником напряжения (ЭДС) . Применив метод наложения (положительные направления выбраны), запишем напряжения и токи (сначала учитываем действие источников затем и далее источников, действующих в цепи):

Так как , то

Конечно, уравнения (14.93) можно получить и из уравнений Кирхгофа исключением токов и напряжений ре-зистивных элементов. Однако совместное решение уравнений Кирхгофа с увеличением числа ветвей цепи становится все более громоздким.
Уравнения состояния можно формировать и сразу в матричной форме.
Если источников тока и ЭДС нет, т. е. F = 0, то уравнения (14.91) упрощаются

и характеризуют свободные процессы в цепи. Решение запишем в виде

где X (0) - матрица-столбец начальных значений переменных состояния; - матричная экспоненциальная функция.
Подставив (14.94) в (14.91в), убедимся, что получается тождество.
При решение уравнения (14.91) представим в виде

где Ф(t ) - некоторая матричная функция цепи. После дифференцирования (14.95) получим

Сравним (14.96) с (14.91а)

и, умножив на , после интегрирования найдем, что

где q - переменная интегрирования, или



Подставим это выражение в (14.95):



В частности, при t = 0 имеем
Следовательно, решение для переменных состояния записывается в виде


(реакция цепи равна сумме реакций при нулевом входе и при нулевом начальном состоянии).
Это решение можно получить и применив операторный метод расчета переходных процессов, рассматриваемый в разделе .
Выходные величины можно найти по (14.92).
Если состояние цепи задано не при t = 0, а при , то в (14.97) первое слагаемое записывается так: , а нижний предел интеграла не 0, а t .
Главная трудность расчета заключается в вычислении матричной экспоненциальной функции. Один из путей такой: сначала находим собственные значения l матрицы А, т. е. корни уравнения

где 1 - единичная матрица порядка n , которые определяются из уравнения

где - элементы матрицы А.
Собственные значения совпадают с корнями характеристического уравнения цепи.
Матричная экспонента, аргумент которой - матрица А t , имеющая порядок n , представима конечным числом n слагаемых. Если собственные значения различны, то

Где - функции времени; и т. д.
Далее для определения составляем алгебраическую систему n уравнений

Наконец, определив из (14.100), по (14.99) находим и затем X (t) по (14.97).

Пример 14.6. Определить ток в цепи на рис. 14.42 после коммутации при .

Решение. Выбираем положительные направления токов в индуктивных элементах, т. е. переменных состояния, и тока . Независимые начальные условия: . Дифференциальные уравнения цепи

Исключив ток , получим уравнения относительно производных переменных состояния:

т. е. согласно (14.91)

и матрица-столбец начальных значений

Вычислим собственные значения; по (14.98)

откуда . Если приравнять нулю главный определитель уравнений с переменными состояния, то получим те же значения .
Находим коэффициенты ак по (14.100), т. е. из системы уравнений

Значения тока вычисленные в моменты секунд для интервала времени 0 - 0,1 с, в конце которого ток отличается от установившегося менее чем на 1,5%, приведены в табл. 14.1. При вычислениях цифры записывались с 8 разрядами, а во всех приведенных в примере формулах и в табл. 14.1 указаны с округлением.

Таблица 14.1

	0,005	0,010	0,015	0,020	0,025	0,030	0,035	0,040	0,045	0,050
	1,079	1,213	1,343	1,455	1,550	1,628	1,692	1,746	1,790	1,827
	0,055	0,060	0,065	0,070	0,075	0,080	0,085	0,090	0,095	0,100
, то для n - q разных корней составляется система (14.100), а для q кратных уравнения получаются после вычисления первых q - 1 производных по от обеих частей уравнения с корнем , т. е. Если в цепи действует только один источник ЭДС (или тока), представляющий единичный скачок 1( t ), т. е. F(t )=1(t ), и начальные условия нулевые, то решение (14.97) запишется в виде Для выходных величин по (14.92а) получим Это будут переходные функции цепи h(t). Импульсные переходные функции k (t ) определяются по (14.84) или (14.85). Более общим путем вычисления матричной экспоненциальной функции служит ее представление бесконечным рядом но ряд при больших t медленно сходится. При ограничении конечным числом слагаемых вычисление сводится к умножению и суммированию матриц. Такие операции есть в математическом обеспечении ЭВМ. Известен метод вычисления матричной экспоненциальной функции, основанный на критерии Сильверста. Уравнения состояния цепей, порядок которых больше двух-трех, проще решаются не аналитическими, а численными методами, дающими возможность автоматизировать расчет в случае применения ЭВМ.

Уравнениями состояния электрической цепи называют любую систему дифференциальных уравнений, которая описывает состояние (режим) данной цепи. Например, система уравнений Кирхгофа является уравнениями состояния цепи, для которой она составлена.

В более узком смысле в математике уравнениями состояния называют систему дифференциальных уравнений 1-го порядка, разрешенных относительно производных (форма Коши). Система уравнений состояния в обобщенной форме имеет вид:

Та же система уравнений в матричной форме:

или в обобщённой матричной форме:

Система уравнений состояния формы Коши решается методом численного интегрирования (метод Эйлера или метод Рунге-Кутта) на ЭВМ по стандартной программе, которая должна быть в пакете стандартных программ. При отсутствии такой программы в пакете она легко может быть составлена по следующему алгоритму (метод Эйлера) для к-го шага:

Значения производных на к-ом шаге:

Значения переменных на к-ом шаге:

Для определения значений переменных и их производных на 1-м шаге ин¬тегрирова¬ния используются их значения на момент t=0, т.е. их начальные условия x1(0), x2(0)...xn(0).

Уравнения состояния формы Коши для заданной схемы могут быть получены из системы уравнений Кирхгофа путем их преобразования. Для этой цели: а) из системы уравнений Кирхгофа методом подстановки исключаются ""лишние"" переменные, имеющие зависимые начальные условия, и оставляют переменные iL(t) и uC(t), которые не изменяются скачком и имеют независи-мые начальные условия iL(0) и uC(0); б) оставшиеся уравнения решаются относительно производных и приводятся их к форме Коши.

В случае сложных схем уравнения состояния формы Коши могут быть составлены топологическими методами с использованием матриц соединений [A] и [B].

Последовательность расчета переходного процесса методом переменных состояния выглядит так:

1. Производится расчет схемы в установившемся режиме до коммутации и определяются независимые начальные условия iL(0) и uC(0).

2. Составляется система дифференциальных уравнений по законам Кирхгофа для схемы после коммутации.

3. Методом исключения ""лишних"" переменных система уравнений Кирхгофа преобразуется в систему уравнений Коши, составляются матрицы коэффициентов.

4. Выбирается расчетное время (продолжительность переходного процесса) и число шагов интегрирования N.

5. Решение задачи выполняется на ЭВМ по стандартной программе. Выходную функцию получают в виде графической диаграммы x=f(t)или в виде таблицы координат функций для заданных моментов времени.

Пример. Для схемы рис. 74.1 с заданными параметрами элементов (e(t)=Emsin(ωt+ψE), R, R1, R2, R3, L1, L2, C) выполнить расчет переходного процесса и определить функцию uab(t).

1. Выполняется расчет схемы в установившемся режиме переменного тока до коммутации и определяются начальные условия i1(0), i2(0), uC(0).

2. Составляется система дифференциальных уравнений по законам Кирхгофа:

3. Система уравнений Кирхгофа преобразуется в систему уравнений Коши.

Для этой цели из (1) выражаем

и делаем подстановку в (1) и (2), а из (4) делаем подстановку в (1). Тогда получим:

Введем обозначения.

Зная реакцию цепи на единичное возмущающее воздействие, т.е. функцию переходной проводимости или (и) переходную функцию по напряжению , можно найти реакцию цепи на воздействие произвольной формы. В основе метода – метода расчета с помощью интеграла Дюамеля – лежит принцип наложения.

При использовании интеграла Дюамеля для разделения переменной, по которой производится интегрирование, и переменной, определяющей момент времени, в который определяется ток в цепи, первую принято обозначать как , а вторую - как t.

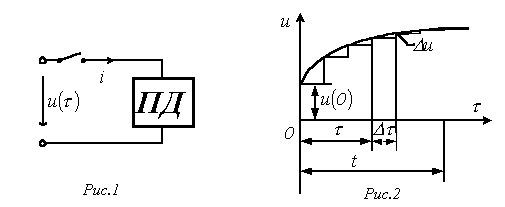
Пусть в момент времени к цепи с нулевыми начальными условиями (пассивному двухполюснику ПД на рис. 1) подключается источник с напряжением произвольной формы. Для нахождения тока в цепи заменим исходную кривую ступенчатой (см. рис. 2), после чего с учетом, что цепь линейна, просуммируем токи от начального скачка напряжения и всех ступенек напряжения до момента t, вступающих в действие с запаздыванием по времени.

В момент времени t составляющая общего тока, определяемая начальным скачком напряжения , равна .

В момент времени имеет место скачок напряжения , который с учетом временного интервала от начала скачка до интересующего момента времени t обусловит составляющую тока .

Полный ток в момент времени t равен, очевидно, сумме всех составляющих тока от отдельных скачков напряжения с учетом , т.е.

Заменяя конечный интервал приращения времени на бесконечно малый, т.е. переходя от суммы к интегралу, запишем

.

(1)

Соотношение (1) называется интегралом Дюамеля.

Следует отметить, что с использованием интеграла Дюамеля можно определять также напряжение. При этом в (1) вместо переходной проводимости будет входить переходная функция по напряжению.

Последовательность расчета с использованием
интеграла Дюамеля

В качестве примера использования интеграла Дюамеля определим ток в цепи рис. 3, рассчитанный в предыдущей лекции с использованием формулы включения.

Исходные данные для расчета: , , .

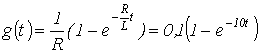
Полученный результат аналогичен выражению тока, определенному в предыдущей лекции на основе формулы включения.

Метод переменных состояния

Уравнения элекромагнитного состояния – это система уравнений, определяющих режим работы (состояние) электрической цепи.

Метод переменных состояния основывается на упорядоченном составлении и решении системы дифференциальных уравнений первого порядка, которые разрешены относительно производных, т.е. записаны в виде, наиболее удобном для применения численных методов интегрирования, реализуемых средствами вычислительной техники.

Количество переменных состояния, а следовательно, число уравнений состояния равно числу независимых накопителей энергии.

К уравнениям состояния выдвигаются два основных требования:

Независимость уравнений;

Возможность восстановления на основе переменных состояния (переменных, относительно которых записаны уравнения состояния) любых других переменных.

Первое требование удовлетворяется специальной методикой составления уравнений состояния, которая будет рассмотрена далее.

Для выполнения второго требования в качестве переменных состояния следует принять потокосцепления (токи в ветвях с индуктивными элементами) и заряды (напряжения) на конденсаторах. Действительно, зная закон изменения этих переменных во времени их всегда можно заменить источниками ЭДС и тока с известными параметрами. Остальная цепь оказывается резистивной, а следовательно, всегда рассчитывается при известных параметрах источников. Кроме того, начальные значения этих переменных относятся к независимым, т.е. в общем случае рассчитываются проще других.

При расчете методом переменных состояния, кроме самих уравнений состояния, связывающих первые производные и с самими переменными и и источниками внешних воздействий – ЭДС и тока, необходимо составить систему алгебраических уравнений, связывающих искомые величины с переменными состояния и источниками внешних воздействий.

Таким образом, полная система уравнений в матричной форме записи имеет вид

;

(2)

.

(3)

Здесь и - столбцовые матрицы соответственно переменных состояния и их первых производных по времени; - матрица-столбец источников внешних воздействий; - столбцовая матрица выходных (искомых) величин; - квадратная размерностью n x n (где n – число переменных состояния) матрица параметров, называемая матрицей Якоби; - прямоугольная матрица связи между источниками и переменными состояния (количество строк равно n, а столбцов – числу источников m); - прямоугольная матрица связи переменных состояния с искомыми величинами (количество строк равно числу искомых величин к, а столбцов – n); - прямоугольная размерностью к x m матрица связи входа с выходом.

Начальные условия для уравнения (2) задаются вектором начальных значений (0).

В качестве примера составления уравнений состояния рассмотрим цепь на рис. 4,а, в которой требуется определить токи и .

По законам Кирхгофа для данной цепи запишем

;

(4)

;

(5)

Матричное уравнение вида (3) вытекает из соотношений (4) и (6):

С

D

Вектор начальных значений (0)= .

Непосредственное использование законов Кирхгофа при составлении уравнений состояния для сложных цепей может оказаться затруднительным. В этой связи используют специальную методику упорядоченного составления уравнений состояния.

Методика составления уравнений состояния

Эта методика включает в себя следующие основные этапы:

1. Составляется ориентированный граф схемы (см. рис. 4,б), на котором выделяется дерево, охватывающее все конденсаторы и источники напряжения (ЭДС). Резисторы включаются в дерево по необходимости: для охвата деревом всех узлов. В ветви связи включаются катушки индуктивности, источники тока и оставшиеся резисторы.

2. Осуществляется нумерация ветвей графа (и элементов в схеме), проводимая в следующей последовательности: первыми нумеруются участки графа (схемы) с конденсаторами, затем резисторами, включенными в дерево, следующими нумеруются ветви связи с резисторами и, наконец, ветви с индуктивными элементами (см. рис. 4,б).

3. Составляется таблица, описывающая соединение элементов в цепи. В первой строке таблицы (см. табл. 1) перечисляются емкостные и резистивные элементы дерева, а также источники напряжения (ЭДС). В первом столбце перечисляются резистивные и индуктивные элементы ветвей связи, а также источники тока.

Таблица 1 . Таблица соединений

Процедура заполнения таблицы заключается в поочередном мысленном замыкании ветвей дерева с помощью ветвей связи до получения контура с последующим обходом последнего согласно ориентации соответствующей ветви связи. Со знаком «+» записываются ветви графа, ориентация которых совпадает с направлением обхода контура, и со знаком «-» ветви, имеющие противоположную ориентацию.

Осуществляется расписывание таблицы по столбцам и по строкам. В первом случае получаются уравнения по первому закону Кирхгофа, во втором – по второму.

В рассматриваемом случае (равенство тривиально)

,

откуда в соответствии с нумерацией токов в исходной цепи

.

При расписывании таблицы соединений по строкам напряжения на пассивных элементах необходимо брать со знаками, противоположными табличным:

(7)

Эти уравнения совпадают соответственно с соотношениями (6) и (5).

Из (7) непосредственно вытекает

.

Таким образом, формализованным способом получены уравнения, аналогичные составленным выше с использованием законов Кирхгофа.

Литература

1. Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
2. Матханов П.Н. Основы анализа электрических цепей. Линейные цепи.: Учеб. для электротехн. радиотехн. спец. вузов. 3-е изд., перераб. и доп. –М.: Высш. шк., 1990. –400с.

Контрольные вопросы и задачи

А
В