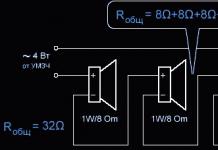
Сьогодні ми детальніше розглянемо пристрій віртуальної камери. Почнемо з картинки.
На малюнку бачимо координатний простір камери. Напрямок ("погляд") камери завжди збігається з позитивним напрямом осі z, а сама камера розташована на початку координат.
Внутрішній простір піраміди зображеної на малюнку - це частина віртуального світу, яку побачить користувач.
Зверніть увагу на три поверхні. Перша розташована з відривом 1 по осі z. Це близька площина. Те, що знаходиться до неї гравець ніколи не побачить. У даному випадкузначення z дорівнює одиниці, але взагалі кажучи, воно може бути будь-яким. Саме із ближньою площиною пов'язаний один дефект відображення графіки. Цей дефект проявляється насамперед у шутерах (через велику свободу камери). Коли ти надто близько підходиш до об'єкта, то можна опинитися "всередині". З останніх ігорцей дефект особливо сильно виявлявся в Left 4 dead: коли на гравця напалювали натовп зомбі, то дуже часто можна було зазирнути всередину інших персонажів.
Площина розташована з відривом 100 одиниць по осі z називається далекою. Знову ж таки, значення може бути довільним. Користувач ніколи не побачить об'єкти, розташовані далі цієї площини.
Шість площин, що обмежують простір, який побачить користувач, називаються відсікаючими (clipping planes): ліва права верхня нижня ближня і дальня.
Площина розташована між ближньою та далекою – проекційна. Надалі, цю площину ми розташовуватимемо в z=1, тобто. вона співпадатиме з ближньою. Тут я відокремив ближню та проекційну площини, щоб показати, що це все-таки не одне й те саме. Проекційна площина призначена для останнього перетворення координат: перетворення з тривимірного простору камери - двомірне простір.
Саме завдяки проекційній площині користувач побачить віртуальний світ. Власне, ця площина є те, що побачить користувач. p align="justify"> Проекційна площина безпосередньо пов'язана з такими поняттями як основний/фоновий буфери, вікно програми та екран користувача. Усі ці поняття можна як прямокутну картинку, що у пам'яті комп'ютера представлена масивом цифр.
Перетворення координат із тривимірного світу на проекційну площину - найскладніше з тих, які на Наразібули нами вивчені.
Поле зору/зона огляду (field of view)
На малюнку вище у проекційній площині (а значить і зображення, яке побачить користувач) ширина більше висоти. Ширина та висота проекційної площини задаються за допомогою кутів. Зустрічаються різні назвицих кутів: поля зору чи зони огляду. В англійській - fields of view. 
Зони огляду задаються двома кутами. Назвемо їх: fovx – зона огляду по горизонталі, fovy – зона огляду по вертикалі. Детально про зони огляду: нижче.
Z-буфер / w-буфер / буфер глибини (z-buffer / w-buffer / depth buffer)
Подивимося на картинку, на якій представлено два трикутники: на відстані 25 і 50 одиниць від камери. На малюнку (а) показано розташування трикутників у просторі (вид зверху), а на малюнку (б) можна побачити кінцеве зображення: 
Як ви можливо здогадуєтеся, зображення потрібно малювати починаючи з найдальших елементів і закінчуючи найближчими. Очевидне рішення: обчислити відстань від початку координат від камери до кожного об'єкта, а потім порівняти. У комп'ютерної графікивикористовується трохи більш удосконалений механізм. Цей механізм має кілька назв: z-буфер, w-буфер, буфер глибини. Розмір z-буфера за кількістю елементів збігається із розміром фонового та основного буферів. У z-буфер заноситься z-компонента найближчого до камери об'єкта. У даному прикладіТам де синій трикутник перекриває зелений, в буфер глибини будуть занесені z-координати синього. Ми ще поговоримо про z-буфери докладніше в окремому уроці.
Ортографічна/паралельна проекція (orthographic/parallel projection)
Операція коли він відбувається зменшення розмірності простору (було тривимірне простір, стало двомірним) називається проекцією. Насамперед нас цікавить перспективна проекція, але сналача ми познайомимося з паралельною (parallel або orthographic projection). 
Для обчислення паралельної проекції достатньо відкинути зайву координату. Якщо ми маємо точку у просторі [ 3 3 3 ], то за паралельної проекції на площину z=1, вона спроектується на точку .
Перспективна проекція (perspective projection) на проекційну площину
У цьому вигляді проекції всі лінії сходяться на одній точці. Саме так влаштований наш зір. І саме за допомогою перспективної проекції моделюється "погляд" у всіх іграх.

Порівняйте цей малюнок з малюнком, що показує однорідні координати з попереднього уроку. Щоб із тривимірного простору перейти у двовимірне, потрібно перші дві компоненти векторів розділити на третю: [x/zy/zz/z] = [x/zy/z1].
Як я вже писав вище, проекційна площина може розташовуватися де завгодно між ближньою та дальньою. Ми завжди розміщуватимемо проекційну площину z=1, але в цьому уроці ми розглянемо й інші варіанти. Подивимося на картинку:

Відстань до проекційної площини від початку координат позначимо як d. Ми розглянемо два випадки: d=1 та d=5. Важливий момент: третя компонента всіх векторів після проекції повинна дорівнювати d - всі точки розташовані в одній площині z = d. Цього можна досягти, помноживши всі компоненти вектора на d: [ xd/z yd/z zd/z ]. При d=1 ми отримаємо: [ x/z y/z 1 ], саме ця формула використовувалася для перетворення однорідних координат.
Тепер, якщо ми відсунемо проекційну площину в точку z = 5 (відповідно d = 5), ми отримаємо: [xd/z yd/zzd/z] = [5x/z5y/z5]. Остання формула проектує всі вектори простору одну площину, де d=5.
В нас тут невелика проблемка. Попередня формула працює із тривимірними векторами. Але ми домовилися використати чотиривимірні вектори. Четверту компоненту у разі можна просто відкинути. Але ми цього не робитимемо, оскільки її використання дає деякі специфічні можливості, які ми ще обговоримо.
Потрібно знайти спільний дільник третьої та четвертої компонент, при розподілі на який у третій компоненті залишається значення d, а в четвертій одиниця. Дільник цей – d/z. Тепер із звичайного вектора [xyz1] нам потрібно отримати вектор готовий до проекції (поділу)[xyzz/d]. Робиться це за допомогою матриці перетворення (перевірте результат помноживши будь-який вектор на цю матрицю):

Останнє перетворення це ще не проекція. Тут ми просто наводимо всі вектори до потрібної форми. Нагадую, що ми розміщуватимемо проекційну площину в d=1, отже вектори виглядатимуть так: [ x y z z ].
Матриця перспективного перетворення
Ми розглянемо матрицю перспективного перетворення, що використовується в DirectX: 
Тепер ми знаємо навіщо призначений елемент _34. Ми також знаємо, що елементи _11 та _22 масштабують зображення по горизонталі та вертикалі. Давайте подивимося, що ховається за іменами xScale і yScale.
Ці змінні залежать від зон огляду, про які ми говорили вище. Збільшуючи або зменшуючи ці кути, можна масштабувати (scale або zoom) зображення - змінювати розмір та співвідношення сторін проекційної площини. Механізм масштабування віддалено нагадає масштабування у фотоапаратах/камерах – принцип дуже схожий. Розглянемо малюнок:

Розділимо кут fov на дві частини та розглянемо лише одну половинку. Що ми бачимо: збільшуючи кут fov/2 (а відповідно і кут fov), ми збільшуємо sin кута і зменшуємо cos. Це призводить до збільшення проекційної площини та відповідно до зменшення спроектованих об'єктів. Ідеальним нам кутом буде fov/2 = P/4. Нагадую, що кут P/4 радіан дорівнює 45 градусам. При цьому fov дорівнюватиме 90 градусам. Чим для нас хороший кут 45 градусів? У разі немає масштабування, а cos(P/4)/sin(P/4)=1.
Тепер ми можемо легко масштабувати картинку по вертикалі (горизонталі), використовуючи синус і косинус половини зони огляду (функція котангенсу C++ називається cot):
yScale = cos(fovY/2)/sin(fovY/2) = cot(fovY/2)
У DirectX використовується тільки вертикальна зона огляду (fovY), а масштабування по горизонатлі залежить від вертикальної зони огляду та співвідношення сторін.
Нагадую, що вікно у наших програмах розміром 500x500. Співвідношення сторін: 1 до 1. Тому змінні дорівнюватимуть: xScale=1, yScale=1.
Співвідношення сторін стандартного монітора/телевізора: 4:3. Цьому співвідношенню відповідають роздільна здатність екрану: 640x480, 800x600, 1600x1200. Ми поки не торкатимемося повноекранного режимуале можемо змінити розмір вікна програми. Ви можете змінити розмір вікна (в present parameters), наприклад, на 640X480. Але щоб всі предмети не розтягнулися (квадрати виглядатимуть як прямокутники), не забудьте змінити відповідні змінні в проекційній матриці.
Ледве не забув, форумула для xScale у DirectX:
xScale = yScale / співвідношення сторін
Співвідношення сторін задаються просто: 1/1, 4/3, 16/9 – це зі стандартних.
Залишилося з'ясувати призначення елементів 33, 34 матриці перспективного перетворення. zf - z-координата далекої площини (від far - далеко), а zn - z-координата ближньої (від near - близько). Зверніть увагу, що елемент _43 = _33*-zn.
Найлегше зрозуміти, що саме роблять ці формули, можна на прикладах. Помножимо стандартний вектор [ x y z w ] на представлену матрицю вище. Рекомендую вам зробити це, взявши аркуш паперу та олівець (сподіваюся ви пам'ятаєте як перемножувати дві матриці). Компоненти вектора набудуть наступного вигляду.
1-а = x*xScale
Друга = y*yScale
3-я = z * (zf / (zf-zn)) + w * (- (zn * zf) / (zf-zn)) = (zf / (zf-zn)) * (z - w * zn)
Четверта = (w*z)/d
Зробимо проекційне перетворення (розділимо всі елементи на 4-у компоненту, при цьому припустимо, що d=1 та w=1):
Перша = (d*x*xScale)/(w*z) = (x*xScale)/z
Друга = (d*y*yScale)/(w*z) = (y*xScale)/z
3-я = (zf/(zf-zn)) * (z - w * zn) * (w * d / z) = (zf / (zf-zn)) * (1 - zn / z)
Четверта = 1
В результаті ми отримали вектор виду:
[ x/(z*xScale) y/(z*yScale) (zf/(zf-zn))*(1-zn/z) 1 ]
Тепер, якщо ви поставите конкретні значення zf і zn, то виявите наступне (для позитивних значень): якщо вектор розташований до ближньої площини, то z-компонента після перетворення буде менше нуля, якщо вектор розташований за дальньою площиною, то z-компонента буде більше одиниці.
Немає ніякої різниці, де саме розташовані ближня і дальня площини: zn=1, zf=10 або zn=10, а zf=100 (або будь-які інші значення) - після перетворення видима область розташовуватиметься у відрізку від нуля до одиниці, включно.
Саме для цього і призначені формули в елементах _33, _34 проекційної матриці - спроектувати відстань від ближньої до дальньої площини у відрізок. Перевірте це, обчисливши значення кількох векторів для конкретних значень zn, zf (так-так, на аркуші паперу!).
У певний моменту будь-якого розробника у сфері комп'ютерної графіки виникає питання: як працюють ці перспективні матриці? Іноді відповідь знайти дуже непросто і, як це зазвичай буває, основна маса розробників кидає це заняття на півдорозі.
Це не вирішення проблеми! Давайте розбиратися разом!
Будемо реалістами з практичним ухилом і візьмемо як піддослідний OpenGL версії 3.3. Починаючи з цієї версії, кожен розробник зобов'язаний самостійно реалізовувати модуль. матричних операцій. Чудово це те, що нам потрібно. Проведемо декомпозицію нашого з вами нелегкого завдання та виділимо основні моменти. Небагато фактів зі специфікації OpenGL:
- Матриці зберігаються по шпальтах (column-major);
- Однорідні координати;
- Канонічний обсяг відсікання (CVV) у лівій системі координат.
Однорідні координати – це не дуже хитра система поруч простих правилз переведення звичних декартових координат до однорідних координат і назад. Однорідна координата це матриця-рядок розмірності. Щоб перевести декартову координату в однорідну координату необхідно x, yі zпомножити на будь-яке дійсне число w(крім 0). Далі необхідно записати результат у перші три компоненти, а останній компонент дорівнюватиме множнику w. Іншими словами:
- Декартові координати
w– дійсне число, що не дорівнює 0 - однорідні координати
Невеликий трюк: Якщо wі одиниці, то все що потрібно для перекладу, це перенести компоненти x, yі zта приписати одиницю в останній компонент. Тобто отримати матрицю-рядок:
Декілька слів про нуль як w. З погляду однорідних координат це цілком припустимо. Однорідні координати дозволяють розрізняти точки та вектори. У декартовій системі координат такий поділ неможливий. - точка, де ( x, y, z) – декартові координати
- Вектор, де ( x, y, z) – радіус-вектор
Зворотний переведення вершини з однорідних координат до декартових координат здійснюється таким чином. Усі компоненти матриці-рядки необхідно поділити на останню компоненту. Іншими словами: - однорідні координати
- Декартові координати
Головне, що необхідно знати, що всі алгоритми OpenGL по відсіканню та розтеризації працюють у декартових координатах, але перед цим усі перетворення виробляються в однорідних координатах. Перехід від однорідних координат до декартових координат здійснюється апаратно.
Канонічний обсяг відсікання або Canonic view volume (CVV) – це одна з мало документованих частин OpenGL. Як видно із рис. 1 CVV - це вирівняний по осях куб з центром на початку координат і довжиною ребра, що дорівнює двійці. Все, що потрапляє в область CVV підлягає растеризації, все, що знаходиться поза CVV, ігнорується. Все, що частково виходить за межі CVV, підлягає алгоритмам відсікання. Найголовніше що треба знати – система координат CVV лівостороння!
Мал. 1. Канонічний обсяг відсікання OpenGL (CVV)
Лівостороння система координат? Як же так, адже у специфікації до OpenGL 1.0 ясно написано, що система координат, що використовується, правостороння? Давайте розумітися.
Мал. 2. Системи координат
Як видно із рис. 2 системи координат відрізняються лише напрямком осі Z. В OpenGL 1.0 справді використовується правостороння користувальницька системакоординат. Але система координат CVV і система координат координат це дві зовсім різні речі. Більше того, починаючи з версії 3.3, більше не існує такого поняття як стандартна системакоординат OpenGL. Як згадувалося раніше, програміст сам реалізує модуль матричних операцій. Формування матриць обертання, формування проекційних матриць, пошук зворотної матриці, множення матриць – це мінімальний набір операцій, які входять у модуль матричних операцій. Виникає два логічні питання. Якщо об'єм видимості це куб із довжиною ребра рівною двом, то чому сцена розміром кілька тисяч умовних одиниць видно на екрані? У який момент відбувається переведення системи координат в систему координат CVV. Проекційні матриці – це якраз та сутність, яка займається вирішенням цих питань.
Головна думка вищевикладеного - розробник сам вільний вибрати тип системи координат і повинен коректно описати проекційні матриці. На цьому з фактами про OpenGL закінчено і настав час зводити все докупи.
Одна з найбільш поширених і складних матриць - це матриця перспективного перетворення. Так як же вона пов'язана з CVV і системою координат користувача? Чому об'єкти зі збільшенням відстані до спостерігача стають меншими? Щоб зрозуміти чому об'єкти зменшуються зі збільшенням відстані, давайте розглянемо матричні перетворення тривимірної моделікрок за кроком. Не секрет, що будь-яка тривимірна модель складається з кінцевого списку вершин, які піддаються матричним перетворенням незалежно один від одного. Для того щоб визначити координату тривимірної вершини на двовимірному екрані монітора необхідно:
- Перевести декартову координату однорідну координату;
- Помножити однорідну координату модельну матрицю;
- Результат помножити на видову матрицю;
- Результат помножити на проекційну матрицю;
- Результат перевести з однорідних координат до декартових координат.
Тепер переходимо до кроку зо три. Тут починає роботу видовий простір. У цьому просторі координати відраховуються щодо положення та орієнтації спостерігача так, начебто він був центром світу. Видовий простір є локальним щодо світового простору, тому координати до нього треба вносити (а не виносити, як у попередньому випадку). Пряме матричне перетворення виносить координати деякого простору. Щоб навпаки внести їх у нього, треба інвертувати матричне перетворення, тому видове перетворення описується зворотною матрицею. Як же отримати цю зворотну матрицю? Спочатку отримаємо пряму матрицю спостерігача. Чим характеризується спостерігач? Спостерігач описується координатою, в якій він знаходиться, та векторами напрямку огляду. Спостерігач завжди дивиться у напрямку своєї локальної осі Z. Спостерігач може переміщатися сценою і здійснювати повороти. Багато в чому це нагадує сенс модельної матриці. За великим рахунком, так воно і є. Однак, для спостерігача операція масштабування безглузда, тому між модельною матрицею спостерігача та модельною матрицею тривимірного об'єкта не можна ставити знак рівності. Модельна матриця спостерігача і є пряма матриця. Інвертувавши цю матрицю, ми отримуємо видову матрицю. Насправді це означає, що це вершини у глобальних однорідних координатах отримають нові однорідні координати щодо спостерігача. Відповідно, якщо спостерігач бачив певну вершину, то значення однорідної координати zцієї вершини у видовому просторі точно буде позитивним числом. Якщо вершина перебувала за спостерігачем, значення її однорідної координати zу видовому просторі точно буде негативним числом.
Крок чотири – це найцікавіший крок. Попередні кроки були розглянуті докладно навмисно, щоб читач мав повну картину про всіх операндах четвертого кроку. На четвертому етапі однорідні координати виносяться з видового простору в простір CVV. Ще раз підкреслюється той факт, що всі потенційно видимі вершини матимуть позитивне значення однорідної координати z.
Розглянемо матрицю виду:
І точку в однорідному просторі спостерігача:
Зробимо множення однорідної координати на матрицю, що розглядається:
Переведемо однорідні координати в декартові координати:
Припустимо, є дві точки у видовому просторі з однаковими координатами xі y, але різними координатами z. Тобто одна з точок знаходиться за іншою. Через перспективне спотворення спостерігач має побачити обидві точки. Справді, з формули видно, що через поділ на координату z, відбувається стиск до точки початку координат. Чим більше значення z(що далі точка від спостерігача), тим сильніше стиск. Ось і пояснення ефекту перспективи.
У специфікації OpenGL сказано, що операції з відсікання та розтеризації виконуються в декартових координатах, а процес переведення однорідних координат в декартові координати проводиться автоматично.
Матриця (1) є шаблоном для матриці перспективою проекції. Як було сказано раніше, завдання матриці проекції полягає в двох моментах: установка системи координат (лівостороння або правостороння), перенесення обсягу видимості спостерігача в CVV. Виведемо перспективну матрицю для лівосторонньої користувальницької системи координат.
Матрицю проекції можна описати з допомогою чотирьохпараметрів (рис. 3):
- Кут огляду в радіанах ( fovy);
- Співвідношення сторін ( aspect);
- Відстань до ближньої площини відсікання ( n);
- Відстань до дальньої площини відсікання ( f).
Мал. 3. Перспективний обсяг видимості
Розглянемо проекцію точки у просторі спостерігача на передню межу відсікання перспективного обсягу видимості. Для більшої наочності на рис. 4 зображено вид збоку. Так само слід врахувати, що система координат координат збігається з системою координат CVV, тобто скрізь користується лівостороння система координат.
Мал. 4. Проеціювання довільної точки
З властивостей подібних трикутників справедливі такі рівності:
Виразимо yꞌ і xꞌ:
У принципі, виразів (2) достатньо отримання координат точок проекції. Однак для правильного екранування тривимірних об'єктів необхідно знати глибину кожного фрагмента. Тобто необхідно зберігати значення компоненти z. Саме це значення використовується для тестів глибини OpenGL. На рис. 3 видно, що значення zꞌне підходить як глибина фрагмента, тому що всі проекції точок вміють однакове значення zꞌ. Вихід із ситуації – використання так званої псевдоглибини.
Властивості псевдоглибини:
- Псевдоглибина розраховується на підставі значення z;
- Чим ближче до спостерігача знаходиться точка, тим менше значення має псевдоглибина;
- У всіх точок, що лежать на передній площині обсягу видимості, значення псевдоглибини дорівнює -1;
- У всіх точок, що лежать на дальній площині відсікання обсягу видимості, значення псевдоглибини дорівнює 1;
- Усі фрагменти, що лежать всередині об'єму видимості, мають значення псевдоглибини в діапазоні [-11].
Коефіцієнти aі bнеобхідно обчислити. Для того, щоб це зробити, скористаємося властивостями псевдоглибини 3 і 4. Отримуємо систему з двох рівнянь із двома невідомими:
Зробимо додавання обох частин системи і помножимо результат на твір fn, при цьому fі nне можуть дорівнювати нулю. Отримуємо:
Розкриємо дужки і перегрупуємо складові так, щоб зліва залишилася тільки частина з а, а справа тільки з b:
Підставимо (6) до (5). Перетворимо вираз до простого дробу:
Помножимо обидві сторони на -2fn, при цьому fі nне можуть дорівнювати нулю. Наведемо подібні, перегрупуємо доданки та висловимо b:
Підставимо (7) у (6) і висловимо a:
Відповідно компоненти aі bрівні:
Тепер підставимо отримані коефіцієнти в матрицю заготівлю (1) і простежимо, що відбуватиметься з координатою zдля довільної точки однорідному просторі спостерігача. Підстановка виконується так:
Нехай відстань до передньої площини відсікання nдорівнює 2, а відстань до дальньої площини відсікання f 10. Розглянемо п'ять точок в однорідному просторі спостерігача:
| Крапка | Значення |
Опис |
|---|---|---|
| 1 | 1 | Крапка знаходиться перед передньою площиною відсікання об'єму видимості. Чи не проходить розтеризацію. |
| 2 | 2 | Крапка знаходиться на передній межі відсікання обсягу видимості. Проходить розтеризація. |
| 3 | 5 | Крапка знаходиться між передньою гранню відсікання і далекою гранню відсікання об'єму видимості. Проходить розтеризація. |
| 4 | 10 | Крапка знаходиться на дальній межі відсікання обсягу видимості. Проходить розтеризація. |
| 5 | 20 | Крапка знаходиться за далекою гранню відсікання обсягу видимості. Чи не проходить розтеризацію. |
Помножимо всі точки на матрицю (8), а потім переведемо отримані однорідні координати декартові координати . Для цього нам необхідно обчислити значення нових однорідних компонентів
і
.
Крапка 1:
Зверніть увагу, що однорідна координата абсолютно правильно позиціонується в CVV, а найголовніше, що тепер можлива робота тесту глибини OpenGL, тому що псевдоглибина повністю відповідає вимогам тестів.
З координатою zрозібралися, перейдемо до координат xі y. Як говорилося раніше, весь перспективний обсяг видимості повинен вміщатися в CVV. Довжина ребра CVV дорівнює двом. Відповідно, висоту та ширину перспективного обсягу видимості треба стиснути до двох умовних одиниць.
У нашому розпорядженні є кут fovyта величина aspect. Давайте виразимо висоту та ширину, використовуючи ці величини.
Мал. 5. Обсяг видимості
З рис. 5 видно, що:
Тепер можна отримати остаточний вигляд перспективної проекційної матриці для лівосторонньої системи координат, що працює з CVV OpenGL:
На цьому висновок матриць закінчено.
Пару слів про DirectX - основного конкурента OpenGL. DirectX відрізняється від OpenGL лише габаритами CVV та його позиціонуванням. У DirectX CVV - це прямокутний паралелепіпед з довжинами по осях xі yрівними двійці, а по осі zдовжина дорівнює одиниці. Діапазон xі yдорівнює [-1 1], а діапазон zдорівнює. Що стосується системи координат CVV, то в DirectX, як і OpenGL, використовується лівостороння система координат.
Для виведення перспективних матриць для правобічної системи координат необхідно перемалювати рис. 2, рис.3 та рис.4 з урахуванням нового напрямку осі Z. Далі розрахунки повністю аналогічні з точністю до знака. Для матриць DirectX властивості псевдоглибини 3 і 4 модифікуються під діапазон.
На цьому тему перспективних матриць вважатимуться закритою.
У комп'ютерній графіці визначені поняття різних матриць. Це світова матриця (World Matrix), матриця виду (View Matrix) та матриця проекції (Projection Matrix). За допомогою даних матриць вихідний кодПрограми проводяться матричні перетворення над моделями. Матричні перетворення мають на увазі під собою множення кожної вершини об'єкта на одну з матриць, а точніше послідовне множення всіх вершин об'єкта на кожну з трьох матриць. Такий підхід дозволяє коректно уявити модель у тривимірному просторі вашого двовимірного монітора. Техніка проходу моделі через три перераховані матриці представляє суть механізму роботи з графічними даними тривимірної площині монітора.
Світова матриця
Світова матриця – дозволяє проводити різні матричні перетворення (трансформацію та масштабування) об'єкта у світовій системі координат. Світова системакоординат – це своя локальна системакоординат даного об'єкта, Якою наділяється кожен об'єкт, скажімо так пройшов через світову матрицю, оскільки кожна вершина бере участь у творі цієї матриці.
Нова локальна система координат значно спрощує афінні перетворення об'єкта у просторі. Наприклад, щоб перенести об'єкт з лівого верхнього кутадисплея в правий нижній кут дисплея, тобто перемістити ігровий об'єкт у просторі, необхідно просто перенести його локальну точкувідліку системи координат на нове місце. Якби не було світової матриці, цей об'єкт довелося переносити по одній вершині. Тому будь-який об'єкт, а точніше, всі вершини цього об'єкта проходять через світову матрицю перетворення.
Як згадувалося, світове перетворення вершин об'єкта може складатися з будь-яких комбінацій обертання, трансляції і масштабування. У математичному записі обертання вершини по осі Х виглядає так:
 Світова матриця
Світова матриця де cos – кут обертання в радіанах.
Обертання вершини навколо осі Y виглядає так:
 Обертання вершини навколо осі Y
Обертання вершини навколо осі Y А обертання навколо осі Z відбувається за такою формулою:
 обертання навколо осі Z
обертання навколо осі Z Трансляція вершини дозволяє перемістити цю саму вершину з координатами x, y, z нову точкуіз новими координатами x1, y1, z1. У математичному записі це виглядає так:
X1 = x + Tx y1 = y + Ty z1 = z + Tz
Трансляція вершини в матричному записі виглядає так:
 Трансляція вершини у матричному записі
Трансляція вершини у матричному записі де Tx, Ty та Tz - значення зміщення по осях X, Y та Z.
Масштабувати вершину в просторі (видаляти або наближати) з координатами x, y, z в нову точку з новими значеннями x1, y1, z1 можна за допомогою наступного запису:
X1 = x * S y1 = y * S z1 = z * S
У матричному записі це виражається так:
 Масштабувати вершину
Масштабувати вершину де Sx, Sy, Sz – значення коефіцієнтів розтягування або стиснення по осях X, Y, Z.
Всі перелічені операції можна робити у вихідному коді програми вручну, тобто обчислювати наведені записи так, як я їх щойно описав. Але звичайно так ніхто не робить (майже ніхто), тому що в DirectX є безліч методів, які зроблять все вище наведені операції за вас.
Матриця виду
Матриця виду – задає місце розташування камери у просторі і це друга за рахунком матриця, яку множаться вершини об'єкта. Ця матриця сприяє визначенню напряму перегляду тривимірної сцени. Тривимірна сцена – це все, що ви бачите на екрані монітора. Це як у театрі, де ви сидите у портері чи на гальорці та спостерігаєте за діями на сцені. Так от сидячи в портері у вас буде одне місце камери, а сидячи на гальорці вже зовсім інше.
Фактично ця матриця дає змогу визначати жанр гри. Наприклад, гра DOOM від першої особи – це можна сказати перші ряди портера у театрі, тоді як гра Warcraft – це гальорка на балконі. Матриця виду призначена для визначення положення камери в просторі, і ви можете зміщувати позицію камери вліво, вправо, вгору, вниз, видаляти, наближати її і таке інше.
Матриця проекції
Матриця проекції – це складніша матриця, що створює проекцію тривимірного об'єктана площину двовимірного екрана монітора. За допомогою цієї матриці визначаються передня та задня області відсікання тривимірного простору, що дозволяє регулювати простір відсікання невидимих на екрані об'єктів, а заодно і знизити навантаження процесора відеокарти. На малюнку зображено механізм проекції об'єкта у площині та відсікання простору.
 Матриця проекції
Матриця проекції На минулій лекції ми говорили про найважливіші проекції, що використовуються в афінній геометрії. Перейдемо тепер до розгляду перспективної геометрії та кількох нових видів проектування.
На фотографіях, картинах, екрані зображення здаються нам природними та правильними. Ці зображення називають перспективними. Властивості їх такі, що віддалені предмети зображуються в менших масштабах, паралельні прямі у випадку непаралельные. У результаті геометрія зображення виявляється досить складною, і готового зображенняскладно визначити розмір тих чи інших частин об'єкта.
Звичайна перспективна проекція - це центральна проекція на площину прямими променями, що проходять через точку - центр проектування. Один із проектуючих променів перпендикулярний до площини проектування і називається головним. Точка перетину цього променя та площини проекції - головна точка картини.
Існує три системи координат. Зазвичай програміст працює та тримає дані про геометричні об'єкти у світових координатах. Для підвищення реалістичності під час підготовки до виведення зображення на екран дані про об'єкти зі світових координат переводять у видові координати. І тільки в момент виведення зображення безпосередньо на екран дисплея переходять до екранних координат, які є номерами пікселів екрану.
Перші дві системи можуть використовуватися в багатовимірних системах координат, але остання лише у двовимірній. Операції є незворотними, тобто із двовимірної картинки-проекції неможливо відновити тривимірне зображення.
Матриця загального перспективного перетворення
У цій матриці елементи a, d, евідповідають за масштабування, m, n, Lза зміщення, p, q, rза проектування, sза комплексне масштабування, хза обертання.
Для детального опису методів відстеження точкових особливостей, калібрування камери та реконструкції тривимірних об'єктівнеобхідно запровадити модель перспективного проектування та описати геометричні властивостіцього перетворення. Точки кількох зображень, отриманих з допомогою перспективної проекції, перебувають у особливих стосунках друг з одним, які описуються эпиполярной геометрией. Моделі цих відносин би мало бути докладно розглянуті, т.к. Майже всі методи тривимірної реконструкції вимагають оцінки відповідних моделей та спираються на їх властивості.
Необхідно відзначити окремо припущення, що у всіх вихідних зображеннях відбито та сама сцена, тобто. кожне зображення є видом сцени з певної камери. Тому для зручності опису вводиться поняття виду як зображення з асоційованою з ним моделлю камери, з якої воно було отримано.
Перспективна проекція
Модель перспективної проекції відповідає ідеальній камері-обскурі. Ця модель досить точно відповідає процесу побудови зображення у більшості сучасних фото- та відеокамер. Однак через обмеження сучасної оптики реальний процес дещо відрізняється від моделі камери-обскури. Відмінності реального процесу від моделі називаються спотвореннями та моделюються окремо.
Модель найпростішої камери-обскури зручна тим, що вона повністю описується центром проекції та положенням площини зображення. Тому проекція будь-якої точки сцени на зображенні може бути знайдена як перетин променя, що з'єднує центр проекції та точку сцени з площиною зображення.
Найпростіша модель перспективної проекції
Розглянемо найпростіший випадок, коли центр проекції камери (фокус) поміщений початку системи координат, і площина зображення збігається з площиною Z=1. Нехай (X,Y,Z) - координати точки в 3-мірному просторі, а (x,y) - проекція цієї точки на зображення I. Перспективна проекція в цьому випадку описується такими рівняннями:
У матричній формі з використанням однорідних координат ці рівняння переписуються у такому вигляді:
 (2.2)
(2.2)
Площина, розташована на відстані 1 від центру проекції, перпендикулярна до оптичної осі називається ідеальною площиною зображення. Оптична вісь перетинає ідеальну площину зображення в точці з званою принциповою точкою. Ілюстрацію найпростішого випадку перспективної проекції наведено на рис. 1.
Внутрішнє калібрування камери
Найпростіший випадок перспективної проекції практично завжди відповідає реальній камері. Відстань від центру проекції до поверхні зображення, тобто. фокусна відстань, що позначається f, зазвичай не дорівнює 1. Також координати точки в площині зображення можуть не збігатися з абсолютними координатами. При використанні цифрової камери, Співвідношення між координатами точки у зображенні та абсолютними координатами точки на ідеальній площині, визначається формою та розмірами пікселів матриці.

Позначимо розміри пікселя матриці цифрової камери за p x , p y , кут нахилу піксела за a, а принципову точку за , рис.2. Тоді координати точки (x, y) у зображенні, що відповідає точці (x R , y R) на ідеальній площині, визначаються виразом:
 (2.3)
(2.3)
Якщо за f x ,f y позначити фокусну відстань f, виміряну в ширинах і висотах пікселів, а tan(α)*f/p y позначити як s, то формула 2.3 перетворюється на:
 (2.4)
(2.4)
Матриця K називається матрицею внутрішнього калібрування камери. Найчастіше в реальних цифрових камер кут нахилу пікселів близький прямому, тобто. параметр s=0, а ширина та висота пікселя рівні. Принципова точка зазвичай знаходиться у центрі зображення. Тому матриця K може бути записана у вигляді:
 (2.5)
(2.5)
Це припущення про вид матриці K широко використовуються для спрощення алгоритмів визначення внутрішнього калібрування камери, а також синтетичного моделювання зображень, необхідних для оцінки якості та ефективності методів тривимірної реконструкції.

Зовнішнє калібрування камери
Нехай M – точка сцени у 3-х мірному просторі. Будь-який рух є евклідовим перетворенням простору, тому в однорідних координатах він виражається як:
 (2.6)
(2.6)
де R - матриця обертання, T = T - вектор перенесення.
Рух камери щодо сцени еквівалентний зворотному руху точок сцени щодо камери, тому одно:
 (2.7)
(2.7)
де R, T - матриця обертання та вектор переміщення камери щодо сцени. Матриця С називається матрицею зовнішнього калібруваннякамери. Матриця C-1 називається матрицею руху камери. Таким чином, матриця зовнішнього калібрування камери переводить координати точок сцени системи координат сцени в систему координат, пов'язану з камерою.
Повна модель перспективної проекції
З виразів 2.1, 2.4, 2.7 можна вивести вираз довільної перспективної проекції для будь-якої камери з довільною орієнтацією та положенням у просторі:

У більш короткій формі з урахуванням попередніх позначень ця формула може бути записана як:

Матриця P називається матрицею проекції камери.
За аналогією із загальним перспективним перетворенням розглянемо спочатку найпростіший випадок перспективного перетворення площини. Нехай площина p збігається з площиною Z=0 тоді однорідні тривимірні координати будь-якої її точки M=. Для будь-якої камери з матрицею проекції P перспективне перетворення площини описується матрицею розмірності 3*3:


Оскільки будь-яку площину в 3-мірному просторі можна перевести в площину Z = 0 евклідовим перетворенням повороту і перенесення, що еквівалентно домноження матриці камери P на матрицю перетворення L, то перспективне відображення довільної площини в просторі описується лінійним перетворенняміз матрицею розмірності 3*3.
Перспективне перетворення площини також називається гомографією. У матричній формі перспективне перетворення площини записується як m=HM.

Геометрія двох зображень
Сцена, що відображена на всіх вихідних зображеннях, вважається нерухомою, тому взаємне розташування проекцій точок сцени на різних кадрах не може змінюватися довільним чином. Обмеження, що накладаються на розташування проекцій точок, очевидно, залежать від параметрів камер та їх положення один щодо одного. Тому визначення моделей таких обмежень дає частину інформації про взаємне розташування камер, з яких було отримано зображення.
Перспективне перетворення площини
Якщо центри двох камер збігаються, то точки на площинах зображення обох камер перетворюються одна на одну перспективним перетворенням площини. У цьому випадку перетворення точок між зображеннями не залежить від форми 3-мірної сцени, а залежить тільки від взаємного положення площин зображень.

Якщо вся сцена або її частина є площиною, то її зображення на різних видахз центрами камер, що не збігаються, можна перевести один в одного перетворенням гомографії. Нехай p - площина, що спостерігається, H 1 - перетворення гомографії між площиною p і зображенням I 1, H 2 - перетворення гомографії між площиною p та зображенням I 2. Тоді перетворення гомографії H 12 між зображеннями I 1і I 2можна вивести наступним чином:

H 12 залежить від параметризації площини p, отже залежить і від системи координати у просторі
Більшість методів визначення координат 3-х мірних точок за їх проекціями та методів реконструкції 3-х мірної сцени, спираються на припущення про рух центру камери між видами. Тому при збігу центрів камер кількох видів ці методи даватимуть некоректні результати. Такі конфігурації камер повинні виявлятися та оброблятися спеціальним чином.

Оскільки перетворення гомографії записано в однорідних координатах, матриця H визначена з точністю до масштабу. Вона має 8 ступенів свободи і параметризується 8 змінними. Кожна відома пара відповідних точок m 1і m 2на першому та другому зображенні відповідно дає 2 лінійних рівняннявід елементів матриці H. Тому 4 відомих пар відповідних точок достатньо для складання системи лінійних рівнянь з 8 рівнянь з 8 невідомими. За цією системою гомографія H може бути однозначно визначена, якщо жодні три точки не лежать на одній прямій.
Фундаментальна матриця
Розглянемо випадок, коли центри камер двох видів не збігаються. Нехай C 1і C 2- центри двох камер, M - 3-мірна точка сцени, m 1і m 2- проекції точки M на перше та друге зображення відповідно. Нехай П - площина, що проходить через точку M та центри камер C 1і C 2. Площина П перетинає площини зображень першого і другого видно по прямих l 1і l 2. Оскільки промені C 1 Mі C 2 Mлежать у площині П, то очевидно, що точки m 1і m 2лежать на прямих l 1і l 2відповідно. Можна дати більш загальне твердження, що проекції будь-якої точки M", що лежить у площині П, на обидва зображення повинні лежати на прямих l 1і l 2. Ці прямі називаються епіполярними лініями. Площина П називаються епіполярною площиною.

Два види однієї і тієї ж сцени називаються стереопарою, а відрізок C 1 C 2, що з'єднує центри камер, називається базою стереопари (baseline) або стереобазою. Будь-яка епіполярна площина проходить через відрізок C 1 C 2. Нехай C 1 C 2перетинає перше та друге зображення в точках e 1і e 2відповідно. Крапки e 1і e 2називаються епіполярними точками чи епіполями. Усі епіполярні лінії перетинаються у точках e 1і e 2на першому та другому зображенні відповідно. Безліч епіполярних площин є пучок, що перетинається по стереобазі C 1 C 2. Багато епіполярних ліній на обох зображень також являють собою пучки прямих, що перетинаються в e 1і e 2 .
Крапки m 1і m 2називаються відповідними, якщо вони є проекціями однієї точки сцени M. Епіполярні лінії l 1і l 2називаються відповідними, якщо вони лежать в одній і тій самій епіполярній площині П. Якщо епіполярна площина П проходить через точку m 1, тоді епіполярні лінії l 1і l 2, що лежать у ній, називаються відповідними точками m 1.

Обмеження на положення відповідних точок m 1і m 2, що з епіполярної геометрії, можна сформулювати наступним чином: точка m 2, відповідна m 1, має лежати на епіполярній лінії l 2, відповідної m 1. Ця умова називається епіполярним обмеженням. У однорідних координатах умова, що точка mлежить на лінії lзаписується як l T m=0. Епіполярна лінія проходить через епіполярну точку. Рівняння пряме, що проходить через точки m 1і e 1можна записати як:
l 1 ∼ x m 1,
де x- антисиметрична матриця розмірності 3*3 така що, x m 1- векторний витвір m 1і e 1.
Для відповідних епіполярних ліній l 1і l 2вірно:

де P +- псевдоінверсія матриці P.
Матриця F називається фундаментальною матрицею. Вона є лінійний оператор, що співставляє кожній точці m 1відповідну їй епіполярну лінію l 2. Для кожної пари відповідних точок m 1і m 2вірно
m T 2 Fm 1 =0
Це формулювання епіполярного обмеження через фундаментальну матрицю.
Фундаментальна матриця має 7 ступенів волі. Кожна пара відповідних точок m 1і m 2задає одне лінійне рівняння на елементи матриці, тому вона може бути обчислена за відомими 7 пар відповідних точок.
Епіполярне обмеження є справедливим для будь-яких пар відповідних точок, розташованих на ідеальних площинах двох видів. Якщо відомі матриці внутрішнього калібрування K 1і K 2камер обох видів, то епіполярне обмеження для відповідних точок на ідеальних площинах записується як:

Матриця E називається суттєвоюматрицею. Можна показати, що суттєва матриця може бути отримана з взаємного розташування камер.
Нехай P 1 = (I | 0)і P 2 =(R|-RT)- Дві матриці проектування з калібруванням K = I. Тоді рівняння проектування на ідеальну площину обох камер записуються у вигляді:

Знайдемо епіполярну лінію на другому вигляді, що відповідає точці m" 1на першому. Для цього достатньо спроектувати на другий вид дві точки, що лежать на промені (C 1 ,m" 1)на другий вигляд, наприклад центр першої камери (0,0,0,1) Tі точку на площині нескінченності (x" 1, y" 1, z" 1,0) T. Проекціями цих точок будуть відповідно -RT, і R(x" 1 ,y" 1 ,z" 1 ,0) T. Рівняння епіполярної лінії l 2, що проходить через обидві ці точки задається як векторний твір:
l 2 =RT×R(x" 1 ,y" 1 ,z" 1) T =R(T×(x" 1 ,y" 1 ,z" 1) T)
У матричній формі векторний твір T×(x" 1 ,y" 1 ,z" 1) Tможна записати за допомогою матриці S:

Тоді епіполярне обмеження на точки в ідеальній площині записується як:

Вираз суттєвої матриці через параметри зовнішнього калібрування двох камер використовується для обчислення відносного положення камер.

Геометричні властивості трьох і більше зображень
Нехай C 1,C 2і C 3- Центри трьох видів однієї і тієї ж тривимірної сцени. У цьому випадку епіполярні обмеження накладаються на відповідні точки будь-якої пари видів. Якщо відомі проекції двох точок m 1і m 2на перший і другий вид, положення проекції на третє зображення може бути знайдено як перетин двох епіполярних видів, відповідних точкам m 1і m 2.
За двома відомими проекціями m 1і m 2на два зображення з відомим калібруванням можна визначити положення точки M в просторі. Тому якщо відоме калібрування третього зображення, то проекція точки M на третій вид може бути визначена простою проекцією.
Обмеження, що накладаються на положення відповідних точок більше двох зображень, також можна записати в лінійній формі. Для трьох видів ці обмеження записуються у вигляді трифокального тензора, для чотирьох видів – у формі квадрифокального тензора. Однак обчислення цих обмежень еквівалентне обчисленню калібрування всіх трьох чи чотирьох видів у проективному просторі. У роботі ці види обмежень не використовуються, тому докладніше не розглядаються.