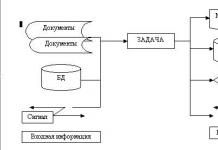
Щоб знайти максимум цільової функції, використовуйте функцію maximize, формат якої наступний maximize(<функция>, <система ограничений>, <опции>);

При цьому умову невід'ємності змінних зручно вказати опцією NONNEGATIVE.

> optimum:=maximize(f,syst_ogr,NONNEGATIVE);

Використовуйте команду subs, яка дозволяє підставити значення змінних x 1 та x 2 у функцію f.

> fmax:=subs(x1=83/17,x2=19/17,f);

Застосуйте функцію evalf для подання відповіді у формі дійсного числа з 4 цифрами.

> fmax:=evalf(fmax,4);

Ознайомитись з варіантом розв'язання задачі ЛП без пояснень можна у додатку.

Вирішення оптимізаційних завдань у спеціалізованому пакеті SimplexWin. http://www.Simplexwin.Narod.Ru/

Ця програма призначена на вирішення завдань лінійного програмування симплекс методом.

Завдання. Знайти значення змінних x 1 і x 2 , при яких

при обмеженнях

Порядок виконання роботи:

Запустіть програму SimplexWin та встановіть необхідний розмір матриці обмежень, вибравши в меню команду Налаштування – Розмір матриці (рис. 13).

Мал. 13. Визначення розміру матриці.

Введіть дані (мал. 14). Якщо завдання вводиться не в канонічної форми, то додаткові змінні та штучні базиси(а також відповідні коефіцієнти цільової функції) додаються автоматично.

Рис.14. Ввід данних.

ІІ. Знаходження оптимального плану та оптимального значення цільової функції.

Мал. 15. Форма результатів.

У формі Результати натисніть кнопку Результат, яка дозволяє зробити розв'язання задачі автоматичному режиміта відобразити на екрані останню симплексну таблицюта результат (рис. 16).

Мал. 16. Рішення завдання.

Вирішення оптимізаційних завдань уExcel

Розглянемо приклад знаходження для наступного завдання лінійного програмування.

Завдання. Знайти значення змінних x 1 і x 2 , при яких

при обмеженнях

Порядок виконання роботи:

I. Оформлення вихідних даних.

Створіть екранну форму для введення умов завдання (змінних, цільової функції, обмежень) та введіть у неї вихідні дані (коефіцієнти цільової функції, коефіцієнти при змінних обмеженнях, праві частини обмежень) (рис. 17).

Мал. 17. Екранна форма завдання (курсор у комірці D6).

Зауваження: В екранній формі на рис. 17 кожної змінної і кожному коефіцієнту завдання поставлена ​​у відповідність конкретна комірка в Excel. Так, наприклад, змінним завдання відповідають осередки B3 ( ), C3 ( ),коефіцієнтам цільової функції відповідають осередки B6 (
), C6 (
), правим частинам обмежень відповідають комірки F10 (
), F11 (
), F12 (
)і т.д.

Введіть залежності з математичної моделіу екранну форму, тобто. введіть формулу для розрахунку цільової функції та формулу для розрахунку значень лівих частин обмежень.

Відповідно до умови завдання значення цільової функції визначається виразом
. Використовуючи позначення відповідних осередків в Excel, формулу для розрахунку цільової функції можна записати як суму творівкожній із осередків, відведених для значень змінних завдання (B3, C3), на відповідні осередки, відведені для коефіцієнтів цільової функції (B6, C6).

Для того, щоб задати формулу залежності для цільової функції, проробіть наступне :

- Поставте курсор в комірку D6;

- Викличте вікно Майстер функцій – крок 1 із 2, натиснувши кнопку на стандартної панеліінструментів;

- у вікні Функціявиберіть функцію СУМПРОВИЗВ;

- У вікні, що з'явилося СУМПРОВИЗВу рядок Масив 1введіть вираз B$3:C$3, а в рядок Масив 2- Вираз B6:С6;

- натисніть кнопку OK.

Мал. 18. Введення формули розрахунку ЦФ у вікні Майстер функцій.

Після введення осередків у рядки Масив 1і Масив 2у вікні СУМПРОВИЗВз'являться числові значеннявведених масивів (рис. 18), а екранній формі з'явиться поточне значення, обчислене за введеною формулою, тобто 0 (оскільки на момент введення формули значення змінних завдання нульові) (рис. 19).

Зауваження: Символ $ перед номером рядка означає, що при копіюванні цієї формули в інші місця аркуша Excel номер рядка 3 не зміниться. Символ : означає, що у формулі використані всі комірки, розташовані між комірками, вказаними ліворуч і праворуч від двокрапки.

Ліві частини обмежень завдання є суму творівкожній із осередків, відведених для значень змінних завдання (B3, C3), на відповідну комірку, відведену для коефіцієнтів конкретного обмеження (B10, C10 – 1 обмеження; B11, C11 – 2 обмеження; B12, C12 – 3 обмеження).

Формули, що задають ліві частини обмежень завдання, відрізняються один від одного і від формули в цільовому осередку D6лише номером рядка у другому масиві. Цей номер визначається тим рядком, в якому обмеження записано в екранній формі. Тому для завдання залежностей для лівих частин обмеження достатньо скопіювати формулу з цільової комірки в комірки лівих частин обмежень.

Для розрахунку значень лівих частин обмежень виконайте таке:

- Поставте курсор в комірку D6та скопіюйте в буфер вміст осередку (клавішами Ctrl+C);

– поставте курсор по черзі на поля лівої частини кожного з обмежень, тобто D10 ,D11 , D12 , і вставляйте в ці поля вміст буфера (клавішами Ctrl+V) (при цьому номер комірок у другому масиві формули змінюватиметься на номер того рядка, в який було зроблено вставку з буфера).

Після введення на екрані на полях D10 ,D11 , D12 з'явиться 0 (нульове значення) (рис. 19).

Мал. 19. Екранна форма завдання після води

всіх необхідних формул.

Перевірте правильність запровадження формул.

Для цього:

- Виконайте по черзі подвійне натисканнялівої клавіші миші на комірки з формулами, при цьому на екрані рамкою виділятимуться комірки, що використовуються у формулі (рис. 20 та рис. 21).

Мал. 20

формули в цільовий осередок D6.

Мал. 20. Перевірка правильності введення

формули в комірку D10 для лівої частини обмежень

Вкажіть цільову функцію та введіть обмеження у вікні Пошук рішення(Рис. 21).

Для цього:

- Поставте курсор в комірку D6;

- Викличте вікно Пошук рішення, вибравши на панелі інструментів Дані - Пошук рішення;

- Поставте курсор у поле Встановити цільовий осередок;

– введіть адресу цільового осередку $D$6або зробіть одне натискання лівою кнопкою миші на цільову комірку в екранній формі, що буде рівнозначно введення адреси з клавіатури;

– вкажіть напрямок оптимізації цільової функції, клацнувши один раз лівою кнопкою миші по селекторній кнопці максимальному значенню;

- у вікні Пошук рішеньв полі Змінюючи коміркивведіть комірки зі значеннями змінних $B$3:$C$3, Виділивши їх в екранній формі, утримуючи ліву кнопку миші;

Мал. 21. Вікно Пошук рішення.

- натисніть кнопку Додати;

– відповідно до умови завдання виберіть у полі знака необхідний знак, наприклад, для 1 обмеження це знак ;

- в полі Обмеженнявведіть адресу комірки правої частини, що розглядається обмеження, наприклад $F$10;

– аналогічно встановіть співвідношення між правими та лівими частинами інших обмежень ( $D$11$F$11 , $D$12$F$12) ;

– підтвердьте введення всіх перерахованих умов натисканням кнопки OK(рис. 22 та рис. 23).

Мал. 22. Додавання умови.

Зауваження: Якщо при введенні умови завдання виникає необхідність у зміні або видаленні внесених обмежень, то це можна зробити натисканням кнопок Змінитиабо видалити.

В умовах ринкової системи управління виробничою та збутовою діяльністю підприємств та фірм в основі прийняття господарських рішень лежить ринкова інформація, а обґрунтованість рішень перевіряється ринком у ході реалізації товарів та послуг. За такого підходу початковим пунктом всього циклу підприємницької діяльності стає вивчення споживчого попиту. Розглянемо деякі питання моделювання попиту та споживання.

Розглянемо споживача, який у результаті існування споживає деякі блага. Рівень задоволення потреб споживача позначимо через U.Припустимо, що є nвидів благ Б 1, Б 2, ..., Б n. Як блага можуть виступати:

· продовольчі товари;

· товари першої необхідності;

· Товари другої необхідності;

· предмети розкоші;

· Платні послуги тощо.

Нехай кількість споживання кожного блага дорівнює х 1 , х 2 ,…, х n. Цільовою функцією споживанняназивається залежність між ступенем (рівнем) задоволення потреб Uі кількістю споживаних благ: х 1 , х 2 , …, х n. Ця функція має вигляд.

У просторі споживчих благ кожному рівнянню відповідає певна поверхня рівноцінних, або байдужих наборів благ, яка називається поверхнею байдужості. Гіперповерхня такої кривої, яка називається багатовимірною поверхнею байдужості, можна уявити у вигляді , де З- Константа. Для наочності розглянемо простір двох благ, наприклад, як двох агрегованих груп товарів: продукти харчування Б 1 і непродовольчі товари, включаючи платні послуги Б 2. Тоді рівні цільової функції споживання можна зобразити на площині у вигляді кривих байдужості, що відповідають різним значенням константи З.Для цього виражають кількість споживання одного блага х 1 через інше х 2 . Розглянемо приклад.

Приклад 6.3. Цільова функціяспоживання має вигляд. Знайти криві байдужості.

Рішення. Криві байдужості мають вигляд або , або (при цьому слід зазначити, що має виконуватися).

Кожен споживач прагне максимізувати рівень задоволення потреб, тобто . Однак максимізації ступеня задоволення потреб заважатимуть можливості споживача. Позначимо ціну на одиницю кожного блага через р 1 , р 2 ,…, р n, а дохід споживача через D.Тоді має виконуватися бюджетне обмеження , що має сенс закону, згідно з яким витрати споживача не повинні перевищувати суму доходу:

У результаті знаходження оптимального набору благ необхідно вирішувати завдання оптимального програмування:

(6.3)

Розглянемо двофакторну функцію споживання, де х 1 - обсяг споживання продуктів харчування та х 2 - споживання непродовольчих товарів та платних послуг. Крім того, припустимо, що весь прибуток споживач спрямовує на задоволення своїх потреб. У цьому випадку бюджетне обмеження міститиме лише два складові, і нерівність перетвориться на рівність. Завдання оптимального програмування при цьому набуде вигляду:

(6.4)

Геометрично оптимальне вирішеннямає сенс точки торкання кривої байдужості лінії, що відповідає бюджетному обмеженню.

х 2

p align="justify"> З бюджетного обмеження системи (6.4) можна висловити змінну . Підставивши цей вираз у цільову функцію, отримуємо функцію однієї змінної , максимум якої можна визначити з рівняння, прирівнявши похідну до нуля: .

Приклад 6.4. Цільова функція споживання має вигляд . Ціна на благо Б 1дорівнює 20, ціна на благо Б 2дорівнює 50. Дохід споживача становить 1800 одиниць. Знайти криві байдужості, оптимальний набірблаг споживача, функцію попиту перше благо за ціною, функцію попиту перше благо за доходом.

Рішення.Криві байдужості мають вигляд:

Отримуємо безліч гіпербол, розташованих у першій координатній чверті на різній відстанівід початку координат залежно від значення константи З.

Знаходимо оптимальний набір благ. Завдання оптимального програмування має вигляд:

Для її вирішення виражаємо з бюджетного обмеження одну змінну через іншу: . Підставляємо у цільову функцію

Знаходимо похідну та прирівнюємо її до нуля

Отримуємо.

Таким чином, оптимальний набір благ становлять 30,5 та 23,8 одиниць. Знаходимо тепер функцію попиту перше благо за ціною нього. І тому у бюджетному обмеженні замість фіксованого значення вводимо ціну першого блага , одержуючи рівняння: . Висловлюємо

або , Звідки знаходимо функцію попиту перше благо за ціною: .

Знаходимо тепер функцію попиту перше благо за доходом. Для цього висловлюємо з бюджетного обмеження одну змінну через іншу: . Підставляємо у цільову функцію:

Знаходимо похідну та прирівнюємо її до нуля:

Звідси знаходимо функцію попиту перше благо за доходом

7. Модель
міжгалузевого балансу

Балансові моделі призначені для аналізу та планування виробництва та розподілу продукції на різних рівнях - від окремого підприємства до народного господарства загалом. Якщо згадати історію народного господарства як Радянського Союзуі Росії, і інших розвинених країн, можна спостерігати, що у економіці багатьох держав різний частраплялися економічні кризи різних крайнощів від криз надвиробництва (США, середина ХХ століття) до дефіциту (Росія, кінець ХХ століття). Усі ці економічні кризи пов'язані з порушенням балансу між виробництвом та споживанням. З цих фактів видно, що баланс між виробленою продукцією та споживанням є важливим критеріємяк макроекономіки, так мікроекономіки.

Економіко-математичні моделі балансу намагалися побудувати багато економістів і математиків з самого початку виникнення проблеми, однак, найбільш повну балансову модель вдалося побудувати в 1936 р. американським економістом В. Леонтьєвим (який після революції емігрував до США і за свою модель отримав Нобелівську премію в галузі економіки). Ця модель дозволяла розрахувати баланс між декількома галузями, що взаємодіють, хоча її можна легко узагальнити і для організацій мікроекономіки, наприклад, для обчислення балансу між декількома взаємодіючими підприємствами або між підрозділами одного підприємства (наприклад, цехами одного заводу).

Мета балансового аналізу - відповісти на питання, що виникає в макроекономіці та пов'язане з ефективністю ведення багатогалузевого господарства: яким має бути обсяг виробництва кожної з пгалузей, щоб задовольнити всі потреби у продукції цієї галузі? У цьому кожна галузь виступає, з одного боку, як виробник певної продукції; а з іншого - як споживач продукції і своєї, і виробленої іншими галузями.

Припустимо, що розглядається пгалузей промисловості, кожна з яких виготовляє свою продукцію. Нехай загальний обсяг виробленої продукції i-й галузі дорівнює. Повна вартість продукції, виготовленої i-й галуззю, називатимемо валовим продуктом цієї галузі. Тепер розглянемо, що витрачається продукція, вироблена галуззю. Частина продукції йде на внутрішньовиробниче споживання цією галуззю та споживання іншими галузями, пов'язаними з цією галуззю. Кількість продукції i-ї галузі, призначеної для кінцевого споживання (поза сферою матеріального виробництва) особистого та громадського j-й галуззю, позначимо. Частина, що залишилася, призначена для реалізації у зовнішню сферу. Ця частина називається кінцевим продуктом. Нехай i-я галузь виробляє кінцевого продукту.

Розглянемо процес виробництва протягом певного періоду часу (наприклад, рік). Оскільки валовий обсяг продукції будь-який i-ї галузі дорівнює сумарному обсягу продукції, що споживається nгалузями, і кінцевого продукту, то рівняння балансу між виробництвом та споживанням матиме вигляд

, (i= 1, 2, …, n). (7.1)

Рівняння (7.1) називаються співвідношення балансу.

. (7.2)

Усі раніше розглянуті показники можна записати до основної балансової таблиці:

Галузь	Споживання галузей,	Кінцевий продукт,	Валовий продукт,
		…	n
			…
			…
…		…			…	…
n			…
Чистий продукт			…

В результаті основна балансова таблиця містить чотири матриці: матрицю міжгалузевих виробничих зв'язків

; матрицю валової продукції; матрицю кінцевої продукції та матрицю чистої продукції .

Однією із завдань балансового аналізу є визначення валового продукту, якщо відомий розподіл кінцевого. Для цього введемо коефіцієнти прямих витрат

Вони виходять у результаті розподілу всіх елементів кожного стовпця матриці на відповідний елемент матриці міжгалузевих виробничих зв'язків Х.Коефіцієнти прямих витрат мають сенс кількості споживання продукції j-ї галузі, необхідної для виробництва одиниці продукції i-й галуззю. З виразу (7.3) можна одержати: . Підставивши останній вираз у співвідношення балансу (7.1), отримаємо

. (7.4)

Якщо позначити матрицю коефіцієнтів прямих витрат як , то співвідношення балансу (7.4) матричному виглядіможна записати у вигляді

З останнього виразу можна знайти значення кінцевого продукту за відомого значення валового

де - Поодинока матриця того ж розміру, що і А.

Приклад 7.1. Баланс чотирьох галузей за попередній період має матрицю міжгалузевих виробничих зв'язків виду і матрицю валової продукції виду. Необхідно визначити кінцевий продукт Yта чистий продукт Cкожній галузі.

Кінцевий продукт Yвиходить у результаті віднімання з кожного елемента матриці валової продукції суми елементів відповідних рядків матриці. Наприклад, перше значення дорівнює 100 - (10 + 20 + 15 + 10) = 45. Чистий продукт Звиходить в результаті віднімання з кожного елемента матриці валової продукції Хсуми елементів відповідних стовпців матриці. Наприклад, перше значення дорівнює 100 - (10 + 5 + 25 + 20) = 40. В результаті отримаємо основну балансову таблицю:

Галузь	Споживання галузей,	Кінцевий продукт,	Валовий продукт,
Чистий продукт,					S = 210	S = 400

Поставимо тепер інше завдання: розрахуємо кінцевий продукт кожної галузі на майбутній період, якщо валовий продукт виявиться рівним . Для вирішення цього завдання знайдемо коефіцієнти прямих витрат: i-ї галузі.

Приклад 7.2. У певному регіоні є дві основні галузі народного господарства: машинобудування (м/с) та сільське господарство (с/г). Баланс цих галузей за звітний період визначається матрицями. Обчислимо інші показники та заповнимо основну балансову таблицю

Припустимо, що у майбутній період планується кінцева продукція обсягах . Потрібно визначити, який валовий продукт у своїй потрібно планувати. Знайдемо коефіцієнти прямих витрат:

Можна виділити наступні причини, за якими економічні системи є стохастичними:

1) система складна, багатокритеріальна, описується багаторівневою ієрархічною структурою;

2) система схильна до впливу великої кількостінекерованих зовнішніх факторів (погодні умови, зовнішня політика, соціальні чинникиі т.д.);

3) навмисне спотворення інформації, приховування інформації та цілеспрямована економічна диверсія.

Виходячи з цього для моделювання багатьох економічних системвикористовують математичні методи, засновані на застосуванні законів теорії ймовірностей, які дістали назву стохастичних методів.

При застосуванні стохастичних методів оптимізація цільової функції ведеться за середнім значенням, тобто при заданих параметрахнеобхідно знайти таке рішення, коли значення цільової функції в середньомубуде максимальним.

Стохастичні системи економіки описуються марківським апаратом, основу якого лежать марковские випадкові процеси. Вони застосовуються у випадках, коли не можна заформалізувати модель (описати аналітичним виразом) і у випадку, коли система є багатопараметричною імовірнісною економічною системою.

Визначення. Будь-яке рішення системи обмежень називається допустимим рішенням ЗЛП.
Визначення. Допустиме рішення, в якому цільова функція досягає максимального або мінімального значенняназивається оптимальним рішенням.

У силу цих визначень завдання ЛП може бути сформульовано наступним чином: серед усіх точок опуклої області, що є рішенням системи обмежень, вибрати таку координати якої мінімізують (максимізують) лінійну функцію F = з 1 x + з 2 y.
Зауважимо, що змінні x, yв ЗЛП приймають, як правило, невід'ємні значення ( x≥ 0, y≥ 0), тому область розташована у І чверті координатної площини.

Розглянемо лінійну функцію F = з 1 x + з 2 yі зафіксуємо якесь її значення F. Нехай, наприклад, F= 0, тобто. з 1 x + з 2 y= 0. Графіком цього рівняння буде пряма, яка проходить через початок координат (0; 0) (рис.).
Малюнок
При зміні цього фіксованого значення F = dпряма з 1 x+ з 2 y = dзміщуватиметься паралельно і «закреслить» всю площину. Нехай D– багатокутник – сфера вирішення системи обмежень. При зміні dпряма з 1 x + з 2 y = d, при деякому значенні d = d 1 досягне багатокутника D, назвемо цю точку А"точкою входу", і потім, пройшовши багатокутник, при деякому значенні d = d 2 матимемо з ним останню загальну точку У, назвемо У"точкою виходу".
Очевидно, що свого найменшого і найбільшого значенняцільова функція F=з 1 x + з 2 yдосягне в точках "входу" Ата «виходу» У.
Враховуючи, що оптимальне значення на безлічі допустимих рішень цільова функція набуває у вершинах області D, можна запропонувати наступний план рішення ЗЛП:

1. побудувати сферу рішень системи обмежень;
2. побудувати пряму, відповідну цільовій функції, і паралельним перенесенням цієї прямої знайти точку «входу» або «виходу» (залежно від вимог мінімізувати або максимізувати цільову функцію);
3. визначити координати цієї точки, обчислити їх значення цільової функції.

Зауважимо, що вектор ( з 1 , з 2), перпендикулярний до прямої, показує напрямок зростання цільової функції.

При графічне рішенняЗЛП можливі два випадки, які потребують особливого обговорення.

Випадок 1
Малюнок 6
При переміщенні прямої з 1 x + з 2 y= d"вхід" або "вихід" (як на малюнку) відбудеться по стороні багатокутника. Це станеться, якщо в багатокутнику є сторони, паралельні прямий з 1 х+ з 2 у = d .
У цьому випадку точок «виходу» («входу») безліч, а саме – будь-яка точка відрізка АВ. Це означає, що цільова функція набуває максимального (мінімального) значення не в одній точці, а у всіх точках, що лежать на відповідній стороні багатокутника. D.

Випадок 2
Розглянемо випадок, коли область допустимих значеньнеобмежена.
У разі необмеженої області цільова функція може бути задана таким чином, що відповідна пряма не має точки «виходу» (або «входу»). Тоді максимальне значення функції (мінімальне) ніколи не досягається – кажуть, що функція не обмежена.
Малюнок
Необхідно знайти максимальне значення цільової функції F = 4x + 6y→ max при системі обмежень
Побудуємо область допустимих рішень, тобто. розв'яжемо графічно систему нерівностей. Для цього побудуємо кожну пряму та визначимо напівплощини, задані нерівностями.
x + y = 18

x	12	9
y	6	9

0,5x + y = 12

x	12	18
y	6	3

x= 12 – паралельна осі OY ;
y= 9 – паралельна осі OX ;
x= 0 – вісь OY ;
y = 0 – вісь OX;
x≥ 0 – напівплощина праворуч від осі OY;
y≥ 0 – напівплощина вище осі OX;
y≤ 9 – напівплощина нижче y = 9;
x ≤ 12 – напівплощина ліворуч x = 12;
0,5x + y≤ 12 – напівплощина нижче прямої 0,5 x + y = 12;
x + y≤ 18 – напівплощина нижче прямої x + y = 18.
Малюнок
Перетином всіх цих напівплощин є очевидно, п'ятикутник ОАВСДз вершинами в точках Про(0; 0), А(0; 9), У(6; 9), З(12; 6), Д(12; 0). Цей п'ятикутник утворює область допустимих розв'язків задачі.

Розглянемо цільову функцію завдання F = 4x + 6y→ max.

x	3	0
y	–2	0

Побудуємо пряму, що відповідає значенню функції F = 0: 4x + 6y= 0. Рухатимемо цю пряму паралельним чином. З усього сімейства прямих 4 x+ 6y= const останньою вершиною, через яку пройде пряма при виході за кордон багатокутника, буде вершина З(12; 6). Саме в ній F = 4x + 6yдосягне свого максимального значення.
Значить, при x = 12, y= 6 функція Fдосягає свого максимального значення F= 4 ∙ 12 + 6 ∙ 6 = 84, рівного 84. Точка з координатами (12; 6) задовольняє всі нерівності системи обмежень, і в ній значення цільової функції оптимально F* = 84 (оптимальне значення позначатимемо «*»).
Завдання вирішено. Отже, необхідно випустити 12 виробів I виду та 6 виробів II виду, при цьому прибуток складе 84 тис. руб.

Графічний метод застосовується на вирішення завдань, які мали у системі обмежень лише дві змінні. Цей метод може застосовуватися і для систем нерівностей, що мають три змінні. Геометрично ситуація буде інша, роль прямих відіграватимуть площини в тривимірному просторі, а рішенням нерівності від трьох змінних буде напівпростір, що знаходиться по одну сторону від площини. Роль областей гратимуть багатогранники, які є перетином напівпросторів.

Лінійне програмування.

Короткі теоретичні відомості

Постановка завдань

Розв'язання прямого завдання лінійного програмуваннявідповідає на наступне запитання:

за яких інтенсивностей nпроцесів отримання прибутку (надання різних послуг, виробничих процесів), у яких використовуються mвидів ресурсів (факторів виробництва) з відомими граничними інтенсивностями використання цих ресурсів виручка від реалізації (прибуток) буде максимальною у разі, коли інтенсивність витрати кожного ресурсу та інтенсивність отримання прибутку (виручки) у кожному з процесів лінійно залежать від інтенсивності цього процесу.

Вирішення двоїстої до неї задачі відповідає на наступне питання:

за яких найменших цін на одиницю ресурсу економічному агенту буде невигідно подальше розширенняпроцесу отримання прибутку рахунок придбання нових обсягів дефіцитних в умовах економічної діяльності ресурсів.

Пряме завдання лінійного програмування може бути пов'язане з наступною ситуацією. Є n способів отримання прибутку (надання n видів послуг) з обсягами x i (кількість штук i -й наданих послуг). При цьому використовуються m видів ресурсів, запас j -го з яких дорівнює b j . При цьому витрата кожного ресурсу j та величина прибутку в кожному з процесів i лінійно залежать від кількості наданих послуг i -го виду з коефіцієнтами a ji і c i відповідно. Матриця А=(a ji )m ´ n за змістом аналогічна такою ж із першої частини і також називається матрицею технологічних, або структурних коефіцієнтів. Тоді оптимальний за критерієм максимуму отримання прибутку план може бути отриманий з наступної прямої задачі лінійного програмування:

Цьому завданню можна поставити у відповідність розширену матрицю наступного виду:

(4.1)

Подвійне завдання (4) завдання має наступний вигляд (z j - Шукані граничні ціни):

При такому формулюванні двоїстої задачіз умови мінімізації цін випливають (5.1) і (5.3), та якщо з умови невигідності продовження діяльності прямо виникає умова перевищення чи рівності витрат над виручкою від.

Основні поняття моделі

Рішення (план, програма) -набір, вектор конкретних значень всіх змінних параметрів управління моделі – тих величин які може бути змінено з волі керуючого об'єктом моделювання. Рішення бувають допустимі (реалізовані практично), недопустимі (не реалізовані з існуючих моделі обмежень) і оптимальні (найкращі з допустимих).

Цільова функція L(x) - Математичний вираз, що зв'язує фактори (параметри) моделі. Економічний сенсцільової функції відображає критерій оптимальності- Показник, що має економічний зміст і службовець формалізацією конкретної мети управління, наприклад: максимізація прибутку (рядок 1 (4)), максимізація якості продукції або мінімізація витрат (5.1).

Система обмеженьмоделі – межі, що обмежують область допустимих(прийнятних, здійсненних) рішень, що фіксують основні внутрішні та зовнішні властивостіоб'єкти, пов'язані з метою оптимізації. Рівняння зв'язку(типу f j (x) ) - математична формалізація системи обмежень (рядки 2 і 3 в (4), (5.2, 5.3)). Система обмежень відбиває економічний сенс рівнянь зв'язку.

Система, що складається з цільової функції та рівнянь зв'язку, - завдання економіко-математичного моделювання (ЕММ).У разі коли цільова функція та рівняння зв'язку лінійні, а змінні управління змінюються безперервно, завдання ЕММ називається завданням лінійного програмування (ЛП). Основна властивість безлічі допустимих планів (МДП) завдання ЛП – воно є опуклим багатогранником. Випуклим називається безліч, якій належать усі відрізки, що з'єднують будь-які дві точки цієї множини. Якщо завдання ЛП має рішення, воно знаходиться у вершині МДП. Плани, що у вершинах МДП, називаються базовими. Завдання лінійного програмування поділяються на завдання з обмеженнями у формі нерівностей (загальне завдання ЛП) та у формі рівностей (канонічна задача ЛП). При математичної формалізації економічних завдань з допомогою лінійної моделі виходять загальні завдання ЛП – наприклад, (4), (5). Будь-яке загальне завдання шляхом введення додаткових змінних може бути зіставлено канонічна задача. Так, задачі (4) шляхом введення в кожну нерівність типу "витрата ресурсу £ запас ресурсу" (рядок 2 в (4)) додаткової змінної x n+j (Невитрачений залишок j -го ресурсу) зіставляється наступна канонічна:

При цьому розмірність задачі (6) – кількість змінних плану - порівняно з (4) збільшилась з n до n+m .

При розв'язанні задачі (4) важливе значення мають коефіцієнти ресурсовіддачі, серед яких тут будуть використані диференціальні та приростні. Диференціальний коефіцієнт ресурсовіддачі k ji показує вартість наданих під час використання одиниці j -го ресурсу i -их послуг. Ті види послуг, для яких усі k ji виявляються найменшими за всіма видами послуг, є найменш вигідними. Вони не повинні бути присутніми в оптимальному плані. Це дозволяє шляхом примусового обнулення обсягів надання таких послуг знизити розмірність завдання і, таким чином, спростити її вирішення. Обчислюються вони в такий спосіб - k ji = c i /a ji .

прирістний коефіцієнт ресурсовіддачі j – це коефіцієнт пропорційності між збільшенням значення цільової функції оптимального плануі такими, що викликали це збільшення зміною запасів j -го ресурсу Можна вважати, що До j показують, наскільки збільшиться значення цільової функції вихідного завдання в оптимальному плані зі збільшенням величини запасу j -го ресурсу на одиницю З математичної точки зору є повною похідною від оптимального значенняцільової функції за величиною запасу j -го ресурсу: До j = dL opt/db j .

де - Постійні витрати, які не залежать від режиму обробки, хв;

Тут – підготовчо – заключний час на операцію, хв;

Розмір партії оброблюваних деталей;

Допоміжний час операції, хв;

Час обслуговування без урахування часу заміну інструменту, хв;

Час на відпочинок робітника, хв;

Витрати часу, пов'язані із заміною затупленого інструменту та відповідним підналаштуванням технологічної системи;

де - час на заміну інструменту та відповідне розмірне налаштування;

Діаметр і довжина валу, що обробляється;

Коефіцієнт до розрахунку швидкості різання;

Швидкість різання;

Глибина різання;

Тут – показники ступеня у формулах для розрахунку режимів різання.

Аналіз цільової функції часу дозволяє розкрити резерви додаткового підвищення продуктивності та визначити оптимальні режими різання, що забезпечують мінімальні витрати на виконання операції.

Цільова функція вартостіна прикладі обробки валу має вигляд:

Тут - Витрати матеріал;

Витрати в одиницю часу відповідно на експлуатацію обладнання, пристосування із зарплати з урахуванням накладних витрат;

Час на заміну інструменту та відповідне розмірне налаштування;

Вартість інструменту за період експлуатації.

Перший член виразу визначає постійні витрати на матеріал, витрати, пов'язані з підготовчо-заключним часом та часом обслуговування. Другий член виразу визначає витрати на ріжучий інструмент та простої при його заміні. Третій член виразу визначає витрати, пов'язані безпосередньо з виконанням процесу різання.

Об'ємне планування роботи технологічних верстатних систем

Ця та всі наступні лекції присвячені питанням математичного моделювання та оптимізації технологічних верстатних систем.

Об'ємне планування роботи механічної ділянки при досягненні максимального завантаження технологічного обладнання

Постановка задачі. Є m- Верстатів ( m– груп верстатів), на яких можуть бути виготовлені n- Типів деталей. Трудомісткість обробки j- ой деталі на i- м верстаті складає , годину. Відомі фонди часу роботи кожного верстата (групи верстатів) – B i. Вихідні дані для вирішення задачі наведено в таблиці 14.1.

Таблиця 14.1. Вихідні дані для вирішення задачі, представлені у загальному вигляді

Потрібно визначитикількість деталей кожного найменування при обробці яких досягається максимальне завантаження обладнання ділянки.

Математична модельдля вирішення задачі запишеться:

Обмеження:

Завдання вирішується шляхом лінійного програмування. У цьому слід пам'ятати таке. Кількість обмежень виду (14.1) - (14.3) у математичній моделі має суворо дорівнювати кількості верстатів (груп верстатів) ділянки. При вирішенні задачі за допомогою комп'ютера кількість верстатів (груп верстатів), а також типів деталей практично не обмежена і визначається лише можливостями комп'ютера та відповідної програми. При розв'язанні задачі вручну із застосуванням графо-аналітичного методу кількість типів верстатів (груп верстатів) також не обмежена, але їх збільшення природним чином призведе до часу розрахунків. Кількість типів деталей має перевищувати двох, т.к. в іншому випадку неможливо буде на площині виконати необхідні графічні побудови.

приклад.Вихідні дані для прикладу наведені у таблиці 14.2.

Таблиця 14.2. Вихідні дані для вирішення задачі

Позначимо через кількість деталей типу D 1 через кількість деталей типу D 2 .

Математична модельна вирішення цього завдання запишеться так:

Обмеження(за фондом часу роботи обладнання):

Потрібно знайти значення та , що задовольняють заданим обмеженням (14.6) – (14.10) та забезпечують максимум цільової функції (14.11). Параметри і є керованими параметрамиу математичній моделі.

Розв'яжемо завдання графо – аналітичним методом (див. лекцію 6). Графічна ілюстрація розв'язання задачі наведена на рис. 14.1.

Рис.14.1. Графічна ілюстрація розв'язання задачі

Обчислення для побудови обмежень (14.6) – (14.8):

x 1
x 2

x 1
x 2

Провівши пряму лінію, паралельну даній, знаходимо точку торкання її межі ОДР – це точка А. Для знаходження її координат (точки перетину обмежень 14.7 та 14.8) вирішуємо таку систему рівнянь:

Тобто. остаточно

Максимальне значення цільової функції (максимальне завантаження обладнання ділянки) при оптимальних значеннях параметрів, що шукаються, складе:

Завдання про мінімальне завантаження обладнання

Ця та наступні завдання у даній лекції наводяться на рівні постановки задачі та формування математичної моделі для її вирішення. Усі вони вирішуються методами лінійного програмування.

Є mверстатів, на яких можуть бути виготовлені nТипи деталей. Продуктивність i- го верстата при виготовленні деталі j- го типу складає C ij. Величини планових завдань A jна виготовлення j- ой деталі та ресурс часу B iроботи i- го верстата наведено у таблиці 14.3.

Таблиця 14.3 Вихідні дані для вирішення задачі

Потрібно, враховуючи ресурси часу роботи кожного верстата, розподілити завдання між верстатами таким чином, щоб загальний час роботи всіх верстатів був мінімальним.

Нехай t ij- час виготовлення j- ой деталі i- м верстатом. Складемо обмеження ресурсу часу для кожного верстата:

Розв'язання поставленого завдання полягає у мінімізації лінійної цільової функції (сумарного часу)

(14.14)

при обмеженнях (14.12), (14.13) та за умови, що всі змінні .

Завдання про оптимальний розподіл деталей по верстатах

Нехай деяка машина складається із різних видів деталей, які ми пронумеруємо числами. Є типів різних верстатів, причому кількість верстатів - го типу дорівнює . Деталі можуть бути виготовлені на верстатах різного типу. Продуктивність верстатного типу при виготовленні деталі становить . Після виготовлення деталі надходять на збирання. Потрібно закріпити верстати за деталями так, щоб за одиницю часу отримувати максимальну кількість машин.

Нехай - кількість верстатів - го типу, на яких можна виготовити - ю деталь. Очевидно, що кількість верстатів - го типу, що виготовляють деталі видів, не повинна перевищувати задане число:

Загальна кількість комплектів деталей, необхідних для збирання машини, дорівнює загальній кількості будь-якої однієї деталі, що має, наприклад, номер 1. Тому рішення задачі полягає в максимізації лінійної функції

(14.17)

при обмеженнях (14.15), (14,16) з додатковою умовою, що всі змінні .

Знайдені оптимальні значення цього завдання необов'язково цілі числа. Наприклад, означає, що на двох верстатах першого типу протягом одиниці часу виготовлятимуть деталь з номером 1, тоді як третій верстат того ж типу працюватиме лише половину вказаного часу.

Завдання про виробництво продукції за обмежених запасів сировини

З видів сировини виготовляється різних типів продукції. Вартість реалізації виготовленої продукції-го типу становить. Запас сировини - го виду на запланований період дорівнює . Потреба сировини - го типу становить . Вихідні дані для вирішення задачі наведено у таблиці 14.4.

Таблиця 14.4 Вихідні дані для вирішення задачі

Потрібно для кожного типу продукту визначити такий обсяг виробництва, щоб забезпечити максимальну вартість реалізації виготовленої продукції за умови, що не буде перевищено запаси наявної сировини.

Обмеження запасів сировини мають вигляд:

(14.18)

Завдання у тому, щоб визначити оптимальні значення параметрів (змінних) , які у максимум вартість продукції, тобто. цільову функцію

при обмеженнях (14.18) та додаткових умовах .

Основи теорії масового обслуговування

Теорія масового обслуговування становить один із розділів теорії ймовірностей. У цій теорії розглядаються імовірніснізавдання та математичні моделі (до цього нами розглядалися детерміновані математичні моделі). Нагадаємо, що:

Детермінована математична модельвідображає поведінку об'єкта (системи, процесу) з позицій повної визначеностіу теперішньому та майбутньому.

Ймовірнісна математична модельвраховує вплив випадкових чинників поведінка об'єкта (системи, процесу) і, отже, оцінює майбутнє з позицій ймовірності тих чи інших подій.

Тобто. тут як, наприклад, у теорії ігор задачі розглядаються в умовах невизначеності.

Розглянемо спочатку деякі поняття, які характеризують «стохастичну невизначеність», коли невизначені фактори, що входять до завдання, є випадковими величинами (або випадковими функціями), ймовірнісні характеристики яких або відомі, або можуть бути отримані з досвіду. Таку невизначеність називають ще «сприятливою», «доброякісною».

Поняття випадкового процесу

Строго кажучи, випадкові обурення притаманні будь-якому процесу. Простіше навести приклади випадкового, ніж «невипадкового» процесу. Навіть, наприклад, процес ходу годинника (начебто це сувора вивірена робота – «працює як годинник») схильний до випадкових змін (догляд вперед, відставання, зупинка). Але доки ці обурення несуттєві, мало впливають на цікаві для нас параметри, ми можемо ними знехтувати і розглядати процес як детермінований, невипадковий.

Нехай є деяка система S(технічний пристрій, група таких пристроїв, технологічна система – верстат, дільниця, цех, підприємство, галузь промисловості тощо). В системі Sпротікає випадковий процесякщо вона з часом змінює свій стан (переходить з одного стану в інший), причому, заздалегідь невідомим випадковим чином.

Приклади: 1. Система S- технологічна система (дільниця верстатів). Верстати іноді виходять з ладу і ремонтуються. Процес, який у цій системі, випадковий.

2. Система S- Літак, що здійснює рейс на заданій висоті за певним маршрутом. Обурювальні чинники – метеоумови, помилки екіпажу тощо, наслідки – «болтанка», порушення графіка польотів тощо.

Марківський випадковий процес

Випадковий процес, що протікає в системі, називається Марківськимякщо для будь-якого моменту часу t 0 ймовірнісні характеристики процесу в майбутньому залежать тільки від його стану в даний момент t 0 і не залежать від того, коли і як система прийшла до цього стану.

Нехай зараз t 0 система знаходиться у певному стані S 0 . Ми знаємо характеристики стану системи в теперішньому і все, що було при t < t 0 (передісторію процесу). Чи можемо передбачити (передбачити) майбутнє, тобто. що буде за t > t 0? В точності - ні, але якісь ймовірнісні характеристики процесу в майбутньому знайти можна. Наприклад, ймовірність того, що через деякий час система Sвиявиться в стані S 1 або залишиться в стані S 0 і т.д.

приклад. Система S- Група літаків, що беруть участь у повітряному бою. Нехай x– кількість «червоних» літаків, y- кількість "синіх" літаків. На момент часу t 0 кількість літаків, що збереглися (не збитих) відповідно – x 0 , y 0 . Нас цікавить ймовірність того, що в момент часу чисельна перевага буде на боці червоних. Ця ймовірність залежить від того, в якому стані знаходилася система у момент часу t 0 , а не від того, коли і в якій послідовності гинули збиті до моменту t 0 літаки.

На практиці Марківські процеси в чистому виглядізвичайно зустрічаються. Але є процеси, котрим впливом «передісторії» можна знехтувати. І при вивченні таких процесів можна застосовувати Марківські моделі (теоретично масового обслуговування розглядаються і не Марківські системи масового обслуговування, але математичний апарат, який їх описує, набагато складніше).

У дослідженні операцій велике значення мають Марківські випадкові процеси з дискретними станами та безперервним часом.

Процес називається процесом із дискретним станом, якщо його можливі стани S 1 , S 2, … можна заздалегідь визначити, і перехід системи зі стану в стан відбувається «стрибком» практично миттєво.

Процес називається процесом з безперервним часом, якщо моменти можливих переходів зі стану стан не фіксовані заздалегідь, а невизначені, випадкові і можуть статися в будь-який момент.

приклад. Технологічна система(Ділянка) Sскладається з двох верстатів, кожен з яких у випадковий момент часу може вийти з ладу (відмовити), після чого миттєво починається ремонт вузла, що теж триває наперед невідомий, випадковий час. Можливі такі стани системи:

S 0 - обидва верстати справні;

S 1 - перший верстат ремонтується, другий справний;

S 2 - другий верстат ремонтується, перший справний;

S 3 - обидва верстати ремонтуються.

Переходи системи Sзі стану в стан відбуваються практично миттєво, випадкові моментивиходу з ладу того чи іншого верстата чи закінчення ремонту.

При аналізі випадкових процесів із дискретними станами зручно користуватися геометричною схемою – графом станів. Вершини графа – стану системи. Дуги графа - можливі переходи зі стану в

Рис.15.1. Граф станів системи

стан. Для прикладу граф станів наведено на рис.15.1.

Примітка. Перехід із стану S 0 в S 3 малюнку не позначений, т.к. передбачається, що верстати виходять з ладу незалежно один від одного. Імовірністю одночасного виходу з ладу обох верстатів ми нехтуємо.

Потоки подій

Потік подій- Послідовність однорідних подій, що йдуть одна за одною в якісь випадкові моменти часу.

У попередньому прикладі – це потік відмов та потік відновлень. Інші приклади: потік викликів на телефонної станції, Потік покупців у магазині і т.д.

Потік подій можна зобразити поруч точок на осі часу O t- Мал. 15.2.

Рис.15.2. Зображення потоку подій на осі часу

Положення кожної точки випадково, і тут зображена лише одна реалізація потоку.

Інтенсивність потоку подій ()- Це середня кількість подій, що припадає на одиницю часу.

Розглянемо деякі властивості (види) потоків подій.

Потік подій називається стаціонарним, якщо його ймовірні характеристики не залежать від часу.

Зокрема, інтенсивність стаціонарного потоку стала. Потік подій неминуче має згущення чи розрідження, але де вони носять закономірного характеру, і середнє число подій, що припадає на одиницю часу, завжди і від часу залежить.

Потік подій називається потоком без наслідків, якщо для будь-яких двох ділянок часу, що не перетинаються, і (див. рис.15.2) кількість подій, що потрапляють на одну з них, не залежить від того, скільки подій потрапило на іншу. Іншими словами, це означає, що події, що утворюють потік, з'являються в ті чи інші моменти часу незалежно один від одногота викликані кожне своїми власними причинами.

Потік подій називається ординарнимякщо події в ньому з'являються поодинці, а не групами по кілька відразу.

Потік подій називається найпростішим (або стаціонарним пуассонівським),якщо він має відразу три властивості: 1) стаціонарний, 2) ординарен, 3) не має наслідків.

Найпростіший потік має найпростіший математичний опис. Він грає серед потоків таку ж особливу роль, як і закон нормального розподілусеред інших законів розподілу. А саме, при накладенні досить великої кількості незалежних, стаціонарних та ординарних потоків (порівняних між собою за інтенсивністю) виходить потік, близький до найпростішого.

Для найпростішого потоку з інтенсивністю інтервал Tміж сусідніми подіями має так зване показовий (експоненційний) розподілзі щільністю