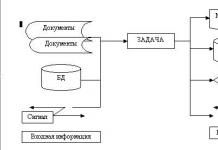
Крок 0. Підготовчий етап.
Наводимо завдання ЛП до спеціальної форми (15).
Крок 1.Складаємо симплекс-таблицю, що відповідає спеціальній формі:
|
|
|
|||||
|
|
|
|
|
|||
|
|
|
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
||
Зауважимо, що цій таблиці відповідає допустиме базове рішення 
Завдання (15). Значення цільової функції у цьому рішенні 
Крок 2Перевірка на оптимальність
Якщо серед елементів індексного рядка симплекс – таблиці 
немає жодного позитивного елемента 
, Оптимальне рішення задачі ЛП знайдено:. Алгоритм завершує роботу.
Крок 3Перевірка на нерозв'язність
Якщо серед 
є позитивний елемент 
, а у відповідному стовпці 
немає жодного позитивного елемента 
, то цільова функція Lє необмеженою знизу на допустимій множині. І тут оптимального рішення немає. Алгоритм завершує роботу.
Крок 4.Вибір провідного стовпця q
Серед елементів 
вибираємо максимальний позитивний елемент 
.Цей стовпець оголошуємо провідним (дозволяючим).
Крок 5.Вибір провідного рядка p
Серед позитивних елементів стовпця 
знаходимо елемент 
, для якого виконується рівність
.
Рядок pоголошуємо провідною (дозволяючою). Елемент 
оголошуємо провідним (дозволяючим).
Крок 6Перетворення симплексної таблиці
Складаємо нову симплекс-таблицю, в якій:
а) замість базисної змінної 
записуємо 
замість небазисної змінної 
записуємо 
;
б) провідний елемент замінюємо зворотною величиною 
;
в) усі елементи провідного стовпця (крім 
) множимо на 
;
г) усі елементи провідного рядка (крім 
) множимо на 
;
д) елементи симплексної таблиці, що залишилися, перетворюються за наступною схемою «прямокутника».
З елемента віднімається добуток трьох співмножників:
перший – відповідний елемент провідного стовпця;
другий – відповідний елемент провідного рядка;
третій – обернена величина провідного елемента 
.
Перетворюваний елемент і відповідні йому три співмножники якраз і є вершинами прямокутника.
Крок 7.Перехід до наступної ітерації здійснюється поверненням кроку 2.
2.3. Алгоритм симплекс-метода для завдання на максимум
Алгоритм симплекс-метода для задачі на максимум відрізняється від алгоритму для задачі на мінімум тільки знаками індексного рядка коефіцієнтів цільової функції 
, а саме:
На кроці 2:
:
На кроці 3
. Цільова функція є необмеженою зверху на допустимій множині.
На кроці 4:
.
2.4. Приклад розв'язання задачі симплекс-методом
Розв'язати задачу, записану у вигляді (15).
Складемо симплексну таблицю:
|
|
|
|
|
|
| |||
|
|
|
Оскільки коефіцієнти рядка цільової функції неотрицательны, то початкове базисне рішення перестав бути оптимальним. Значення цільової функції для цього базису L=0.
Вибираємо провідний стовпець - це стовпець, що відповідає змінній 
.
Вибираємо провідний рядок. Для цього знаходимо 
. Отже, провідний рядок відповідає змінній 
.
Проводимо перетворення симплексної таблиці, вводячи змінну 
в базис і виводячи змінну 
з базису. Отримаємо таблицю:
|
|
|
|
|
|
|
| ||
|
|
|
Одну ітерацію методу завершено. Переходимо до нової ітерації. Отримана таблиця неоптимальна. Базове рішення, відповідне таблиці, має вигляд . Значення цільової функції цьому базисі L=-2.
Ведучий стовпець тут – стовпець, що відповідає змінній 
. Ведучий рядок – рядок, що відповідає змінній 
. Після проведення перетворень отримаємо симплексну таблицю:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ще одну ітерацію завершено. Переходимо до нової ітерації.
Рядок цільової функції не містить позитивних значень, отже, відповідне базисне рішення є оптимальним і алгоритм завершує роботу.
Подвійний симплексний методзаснований на теорії двоїстості (див. рішення двоїстої задачі) і використовується для вирішення задач лінійного програмування, вільні члени яких b i можуть набувати будь-яких значень, а система обмежень задана нерівностями сенсу «≤», «≥» або рівністю «=».Призначення сервісу. Онлайн-калькулятор використовується для вирішення задач лінійного програмування P-методому наступних формах запису: базової формі запису симплекс-метода, у вигляді симплексної таблиці, модифікованим симплекс-методом.
Інструкція для вирішення завдань подвійним симплекс-методом. Виберіть кількість змінних та кількість рядків (кількість обмежень), натисніть Далі. Отримане рішення зберігається у файлі Word (див. приклад рішення двоїстим симплекс-методом).
При цьому обмеження типу x i ≥ 0не враховуйте.Разом із цим калькулятором також використовують такі:
Графічний метод розв'язання ЗЛП
Розв'язання транспортного завдання
Рішення матричної гри
За допомогою сервісу в онлайн режимі можна визначити ціну матричної гри (нижню та верхню межі), перевірити наявність сідлової точки, знайти рішення змішаної стратегії методами: мінімакс, симплекс-метод, графічний (геометричний) метод, методом Брауна.
Екстремум функції двох змінних
Завдання динамічного програмування
Розподілити 5 однорідних партій товару між трьома ринками так, щоб отримати максимальний дохід від їхнього продажу. Дохід від продажу кожному ринку G(X) залежить кількості реалізованих партій товару Х і представлений у таблиці.
| Обсяг товару Х (у партіях) | Прибуток G(X) | ||
| 1 | 2 | 3 | |
| 0 | 0 | 0 | 0 |
| 1 | 28 | 30 | 32 |
| 2 | 41 | 42 | 45 |
| 3 | 50 | 55 | 48 |
| 4 | 62 | 64 | 60 |
| 5 | 76 | 76 | 72 |
У P-методі оптимальний план виходить у результаті руху псевдопланами. Псевдоплан- план, у якому умови оптимальності задовольняються, серед значень базисних змінних x i є негативні числа. Алгоритм двоїстого симплекс-методувключає наступні етапи:
- Складання псевдоплану. Систему обмежень вихідного завдання призводять до системи нерівностей сенсу «?».
- Перевірка плану на оптимальність. Якщо отриманому опорному плані не виконується умова оптимальності, то завдання вирішується симплексним методом .
- Вибір провідних рядка та стовпця. Серед негативних значень базисних змінних вибираються найбільші за абсолютною величиною. Рядок, що відповідає цьому значенню, є провідним.
- Розрахунок нового опорного плану. Новий план виходить внаслідок перерахунку симплексної таблиці методом Жордана-Гаусса. Далі перехід до етапу 2.
Приклад. Підприємству потрібно випустити за планом продукції А1 одиниць, А2 одиниць, А3 одиниць. Кожен вид виробу може проводитись на двох машинах.
Як розподілити роботу машин, щоб загальні витрати часу виконання плану були мінімальні? Дано матрицю витрат і ресурс часу кожної машини. Записати модель досліджуваної операції у формі, що допускає використання P-методу.
Відомо, що вміст n поживних речовин A, B та С у раціоні має бути не менше m1, m2, m3 одиниць відповідно. Зазначені поживні речовини містять три види продуктів. Зміст одиниць поживних речовин, у одному кілограмі кожного з видів продукту наведено у таблиці. визначте денний раціон, що забезпечує отримання необхідної кількості поживних речовин за мінімальних грошових витрат.
Завдання: Розв'язати задачу, використовуючи алгоритм двоїстого симплекс-метода.
Наведемо систему обмежень до системи нерівностей сенсу ≤, помноживши відповідні рядки на (-1).
Визначимо мінімальне значення цільової функції F(X) = 4x1+2x2+x3 за наступних умов-обмежень.
- x 1 - x 2 ≤-10
2x 1 + x 2 - x 3 ≤8
Для побудови першого опорного плану систему нерівностей наведемо до системи рівнянь шляхом запровадження додаткових змінних (перехід до канонічної формі).
У першому нерівності сенсу (≤) вводимо базову змінну x 4 . У другій нерівності сенсу (≤) вводимо базову змінну x 5 .
-1x 1 -1x 2 + 0x 3 + 1x 4 + 0x 5 = -10
2x 1 + 1x 2 -1x 3 + 0x 4 + 1x 5 = 8
Матриця коефіцієнтів A = a(ij) цієї системи рівнянь має вигляд:
| A = |
|
x 4 , x 5 ,
Вважаючи, що вільні змінні дорівнюють нулю, отримаємо перший опорний план:
X1 = (0,0,0,-10,8)
| Базис | B | x 1 | x 2 | x 3 | x 4 | x 5 |
| x 4 | -10 | -1 | -1 | 0 | 1 | 0 |
| x 5 | 8 | 2 | 1 | -1 | 0 | 1 |
| F(X0) | 0 | -4 | -2 | -1 | 0 | 0 |
Ітерація №1
План 0 у симплексній таблиці є псевдопланом, тому визначаємо провідні рядок та стовпець.
Ведучою буде перший рядок, а змінну x 4 слід вивести з базису.
3. Визначення нової базової змінної. Мінімальне значення відповідає 2-му стовпцю, тобто. змінну x 2 необхідно ввести базис.
| Базис | B | x 1 | x 2 | x 3 | x 4 | x 5 |
| x 4 | -10 | -1 | -1 | 0 | 1 | 0 |
| x 5 | 8 | 2 | 1 | -1 | 0 | 1 |
| F(X0) | 0 | -4 | -2 | -1 | 0 | 0 |
| θ | 0 | -4: (-1) = 4 | -2: (-1) = 2 | - | - | - |
4. Перерахунок симплекс-таблиці. Виконуємо перетворення симплексної таблиці методом Жордано-Гаусса.
| Базис | B | x 1 | x 2 | x 3 | x 4 | x 5 |
| x 2 | 10 | 1 | 1 | 0 | -1 | 0 |
| x 5 | -2 | 1 | 0 | -1 | 1 | 1 |
| F(X0) | 20 | -2 | 0 | -1 | -2 | 0 |
Уявимо розрахунок кожного елемента у вигляді таблиці:
| B | x 1 | x 2 | x 3 | x 4 | x 5 |
| -10: -1 | -1: -1 | -1: -1 | 0: -1 | 1: -1 | 0: -1 |
| 8-(-10 1):-1 | 2-(-1 1):-1 | 1-(-1 1):-1 | -1-(0 1):-1 | 0-(1 1):-1 | 1-(0 1):-1 |
| 0-(-10 -2):-1 | -4-(-1 -2):-1 | -2-(-1 -2):-1 | -1-(0 -2):-1 | 0-(1 -2):-1 | 0-(0 -2):-1 |
Ітерація №2
1. Перевірка критерію оптимальності.
План 1 у симплексної таблиці є псевдопланом, тому визначаємо провідні рядок та стовпець.
2. Визначення нової вільної змінної.
Серед негативних значень базисних змінних вибираємо найбільший за модулем.
Ведучою буде другий рядок, а змінну x 5 слід вивести з базису.
3. Визначення нової базової змінної. Мінімальне значення θ відповідає третьому стовпцю, тобто. змінну x 3 необхідно ввести в базис.
На перетині провідних рядка і стовпця знаходиться роздільна здатність (РЕ), рівний (-1).
| Базис | B | x 1 | x 2 | x 3 | x 4 | x 5 |
| x 2 | 10 | 1 | 1 | 0 | -1 | 0 |
| x 5 | -2 | 1 | 0 | -1 | 1 | 1 |
| F(X0) | 20 | -2 | 0 | -1 | -2 | 0 |
| θ | 0 | - | - | -1: (-1) = 1 | - | - |
4. Перерахунок симплекс-таблиці. Виконуємо перетворення.
| Базис | B | x 1 | x 2 | x 3 | x 4 | x 5 |
| x 2 | 10 | 1 | 1 | 0 | -1 | 0 |
| x 3 | 2 | -1 | 0 | 1 | -1 | -1 |
| F(X1) | 22 | -3 | 0 | 0 | -3 | -1 |
| B | x 1 | x 2 | x 3 | x 4 | x 5 |
| 10-(-2 0):-1 | 1-(1 0):-1 | 1-(0 0):-1 | 0-(-1 0):-1 | -1-(1 0):-1 | 0-(1 0):-1 |
| -2: -1 | 1: -1 | 0: -1 | -1: -1 | 1: -1 | 1: -1 |
| 20-(-2 -1):-1 | -2-(1 -1):-1 | 0-(0 -1):-1 | -1-(-1 -1):-1 | -2-(1 -1):-1 | 0-(1 -1):-1 |
У базовому стовпці всі елементи позитивні. Переходимо до основного алгоритму симплекс-метода.
Ітерація №3
1. Перевірка критерію оптимальності.
Серед значень індексного рядка немає позитивних. Тому ця таблиця визначає оптимальний план завдання.
| Базис | B | x 1 | x 2 | x 3 | x 4 | x 5 |
| x 2 | 10 | 1 | 1 | 0 | -1 | 0 |
| x 3 | 2 | -1 | 0 | 1 | -1 | -1 |
| F(X1) | 22 | -3 | 0 | 0 | -3 | -1 |
Оптимальний план можна записати так: x1=0, x2=10, x3=2
F(X) = 2 10 + 1 2 = 22
Один із методів вирішення оптимізаційних завдань ( як правило пов'язаних із знаходженням мінімуму або максимуму) лінійного програмування називається . Симплекс-методвключає цілу групу алгоритмів і способів вирішення завдань лінійного програмування. Один із таких способів, що передбачає запис вихідних даних та їх перерахунок у спеціальній таблиці, носить найменування табличного симплекс-методу.
Розглянемо алгоритм табличного симплекс-метода з прикладу рішення виробничого завдання, яка зводиться до знаходження виробничого плану, що забезпечує максимальний прибуток.
Вихідні дані завдання на симплекс-метод
Підприємство випускає 4 види виробів, опрацьовуючи їх на 3-х верстатах.
Норми часу (хв./шт.) на обробку виробів на верстатах, задані матрицею A:
Фонд часу роботи верстатів (хв.) заданий у матриці B:
Прибуток від продажу кожної одиниці виробу (руб./шт.) заданий матрицею C:
Мета виробничого завдання
Скласти такий план виробництва, за якого прибуток підприємства буде максимальним.
Розв'язання задачі табличним симплекс-методом
(1) Позначимо X1, X2, X3, X4 заплановану кількість виробів кожного виду. Тоді шуканий план: ( X1, X2, X3, X4)
(2) Запишемо обмеження плану як системи рівнянь:
(3) Тоді цільовий прибуток:
Тобто прибуток від виконання виробничого плану має бути максимальним.
(4) Для вирішення завдання на умовний екстремум, замінимо систему нерівностей системою лінійних рівнянь шляхом введення в неї додаткових невід'ємних змінних ( X5, X6, X7).
(5) Приймемо наступний опорний план:
X1 = 0, X2 = 0, X3 = 0, X4 = 0, X5 = 252, X6 = 144, X7 = 80
(6) Занесемо дані в симплекс-таблицю:
В останній рядок заносимо коефіцієнти при цільовій функції та саме її значення зі зворотним знаком;
(7) Вибираємо в останньому рядку найбільше (за модулем) від'ємне число.
Обчислимо b = Н / Елементи_вибраного_стовпця
Серед обчислених значень b вибираємо найменше.
Перетин вибраних стовпчиків і рядків дасть нам роздільну здатність. Змінюємо базис на змінну відповідну роздільну здатність ( X5 на X1).
- Сам роздільний елемент звертається до 1.
- Для елементів роздільної здатності – a ij (*) = a ij / РЕ ( тобто кожен елемент ділимо на значення роздільної здатності елемента і отримуємо нові дані).
- Для елементів роздільного стовпця – вони просто обнуляються.
- Інші елементи таблиці перераховуємо за правилом прямокутника.
a ij (*) = a ij - (A * B / РЕ)
Як бачите, ми беремо поточну комірку, що перераховується, і комірку з роздільним елементом. Вони утворюють протилежні кути прямокутника. Далі перемножуємо значення із осередків 2-х інших кутів цього прямокутника. Цей твір ( A * B) ділимо на роздільний елемент ( РЕ). І віднімаємо з поточного перерахованого осередку ( a ij) те, що вийшло. Отримуємо нове значення - a ij (*).
(9) Знову перевіряємо останній рядок ( c) на наявність негативних чисел. Якщо їх немає – оптимальний план знайдено, переходимо до останнього етапу розв'язання задачі. Якщо є – план ще не оптимальний, і симплекс-таблицю знову потрібно перерахувати.
Так як у нас в останньому рядку знову є негативні числа, починаємо нову ітерацію обчислень.
(10) Так як в останньому рядку немає негативних елементів, це означає, що ми знайдено оптимальний план виробництва! А саме: випускати ми будемо ті вироби, які перейшли до колонки «Базис» – X1 та X2. Прибуток від виробництва кожної одиниці продукції нам відомий ( матриця C). Залишилося перемножити знайдені обсяги випуску виробів 1 та 2 з прибутком на 1 шт., отримаємо підсумкову ( максимальну! ) прибуток при цьому плані виробництва.
ВІДПОВІДЬ:
X1 = 32 шт., X2 = 20 шт., X3 = 0 шт., X4 = 0 шт.
P = 48 * 32 + 33 * 20 = 2196 руб.
Галяутдінов Р.Р.
© Копіювання матеріалу допустиме лише при вказівці прямого гіперпосилання на
. Алгоритм симплекс-методу
Приклад 5.1.Розв'язати таке завдання лінійного програмування симплекс-методом:
Рішення:
I ітерація:
х3, х4, х5, х6 х1,х2. Висловимо базисні змінні через вільні:
Наведемо цільову функцію до наступного виду:
На основі отриманого завдання сформуємо вихідну симплекс-таблицю:
Таблиця 5.3
Вихідна симплекс-таблиця
Оціночні відносини |
||||
Відповідно до визначення базисного рішення вільні змінні дорівнюють нулю, а значення базисних змінних – відповідним значенням вільних чисел, тобто:
3 етап: перевірка сумісності системи обмежень ЗЛП.
На даній ітерації (у таблиці 5.3) ознака несумісності системи обмежень (ознака 1) не виявлено (тобто немає рядка з негативним вільним числом (крім рядка цільової функції), в якому не було б хоча б одного негативного елемента (тобто · негативного коефіцієнта при вільній змінній)).
На даній ітерації (у таблиці 5.3) ознака необмеженості цільової функції (ознака 2) не виявлено (тобто немає колонки з негативним елементом у рядку цільової функції (крім колонки вільних чисел), у якій не було б хоча б одного позитивного елемента) .
Так як знайдене базисне рішення не містить негативних компонентів, воно є допустимим.
6 етап: перевірка оптимальності.
Знайдене базисне рішення не є оптимальним, оскільки згідно з ознакою оптимальності (ознака 4) у рядку цільової функції не повинно бути негативних елементів (вільне число даного рядка при розгляді цієї ознаки не враховується). Отже, згідно з алгоритмом симплекс-метода переходимо до 8 етапу.
Так як знайдене базисне рішення допустиме, то пошук колонки будемо проводити за наступною схемою: визначаємо колонки з негативними елементами в рядку цільової функції (крім колонки вільних чисел). Відповідно до таблиці 5.3 таких колонок дві: колонка « х1і колонка « х2». З таких колонок вибирається та, що містить найменший елемент у рядку цільової функції. Вона і буде вирішальною. Колонка « х2» містить найменший елемент (–3) у порівнянні з колонкою « х1
Для визначення роздільної здатності знаходимо позитивні оціночні відношення вільних чисел до елементів роздільної здатності колонки, рядок, якій відповідає найменше позитивне оцінне відношення, приймається як дозволений.
Таблиця 5.4
Вихідна симплекс-таблиця
У таблиці 5.4 найменше позитивне оцінне відношення відповідає рядку « х5», отже, вона буде вирішальною.
Елемент, розташований на перетин роздільної колонки і рядка, приймається як роздільна здатність. У нашому прикладі – це елемент, який розташований на перетині рядка. х5і колонки « х2».
Дозволяючий елемент показує одну базисну і одну вільну змінні, які необхідно поміняти місцями в симплекс-таблиці, для переходу до нового «поліпшеного» базового рішення. В даному випадку це змінні х5і х2, у новій симплекс-таблиці (таблиці 5.5) їх міняємо місцями.
9.1. Перетворення роздільної здатності елемента.
Роздільний елемент таблиці 5.4 перетворюється таким чином:
Отриманий результат вписуємо до аналогічної клітини таблиці 5.5.
9.2. Перетворення роздільної здатності.
Елементи роздільної здатності таблиці 5.4 ділимо на роздільний елемент даної симплекс-таблиці, результати вписуються в аналогічні осередки нової симплекс-таблиці (таблиці 5.5). Перетворення елементів роздільної здатності наведено в таблиці 5.5.
9.3. Перетворення роздільної здатності колонки.
Елементи роздільної здатності колонки таблиці 5.4 ділимо на роздільний елемент даної симплекс-таблиці, а результат береться зі зворотним знаком. Отримані результати вписуються в аналогічні осередки нової симплекс-таблиці (таблиці 5.5). Перетворення елементів роздільної здатності колонки наведені в таблиці 5.5.
9.4. Перетворення інших елементів симплекс-таблиці.
Перетворення інших елементів симплекс-таблиці (тобто елементів не розміщених у роздільній здатності і колонці) здійснюється за правилом «прямокутника».
Наприклад, розглянемо перетворення елемента, розташованого на перетині рядка « х3» та колонки «», умовно позначимо його « х3». У таблиці 5.4 подумки викреслюємо прямокутник, одна вершина якого розташовується в клітці, значення якої перетворимо (тобто в клітці « х3»), а інша (діагональна вершина) – у клітці з роздільним елементом. Дві інші вершини (другий діагоналі) визначаються однозначно. Тоді перетворене значення клітини х3» дорівнюватиме колишньому значенню даної клітини мінус дріб, у знаменнику якої роздільний елемент (з таблиці 5.4), а в чисельнику добуток двох інших невикористаних вершин, тобто:
« х3»: .
Аналогічно перетворюються значення інших клітин:
« х3 х1»: ;
« х4»: 
;
« х4 х1»: ;
« х6»: 
;
« х6 х1»: ;
«»: 
;
« х1»: 
.
В результаті даних перетворень отримали нову симплекс-таблицю (таблиця 5.5).
II ітерація:
1 етап: складання симплекс-таблиці.
Таблиця 5.5
Симплекс-таблицяII ітерації
Оціночні відносини |
||||
| ||||
|
|
2 етап: визначення базового рішення.
В результаті проведених симплекс-перетворень отримали нове базове рішення (таблиця 5.5):
Як видно, при даному базисному рішенні значення цільової функції = 15, що більше, ніж при попередньому базисному рішенні.
Не сумісність системи обмежень відповідно до ознаки 1 у таблиці 5.5 не виявлено.
4 етап: перевірка обмеженості цільової функції.
Необмеженість цільової функції відповідно до ознаки 2 у таблиці 5.5 не виявлено.
5 етап: перевірка допустимості знайденого базисного рішення.
Знайдене базисне рішення відповідно до ознаки 4 не оптимальне, оскільки у рядку цільової функції симплекс-таблиці (таблиця 5.5) міститься негативний елемент: -2 (вільне число даного рядка при розгляді цієї ознаки не враховується). Отже, переходимо до 8 етапу.
8 етап: визначення роздільної здатності елемента.
8.1. Визначення роздільної здатності колонки.
Знайдене базисне рішення припустиме, визначаємо колонки з негативними елементами рядку цільової функції (крім колонки вільних чисел). Згідно з таблицею 5.5, такою колонкою є лише одна колонка: « х1». Отже, її приймаємо як дозволену.
8.2. Визначення роздільної здатності рядка.
Згідно з отриманими значеннями позитивних оціночних відносин у таблиці 5.6, мінімальним є відношення, що відповідає рядку « х3». Отже, її приймаємо як дозволену.
Таблиця 5.6
Симплекс-таблицяII ітерації
Оціночні відносини |
||||
3/1 = 3 - min |
||||
9 етап: перетворення симплекс-таблиці.
Перетворення симплекс-таблиці (таблиці 5.6) виконуються аналогічно, як і попередньої ітерації. Результати перетворень елементів симплекс-таблиці наведено у таблиці 5.7.
III ітерація
За результатами симплекс-перетворень попередньої ітерації складаємо нову симплекс-таблицю:
Таблиця 5.7
Симплекс-таблицяIII ітерації
Оціночні відносини |
||||
| ||||
|
|
2 етап: визначення базового рішення.
В результаті проведених симплекс-перетворень отримали нове базове рішення (таблиця 5.7):
3 етап: перевірка сумісності системи обмежень.
Не сумісність системи обмежень відповідно до ознаки 1 у таблиці 5.7 не виявлено.
4 етап: перевірка обмеженості цільової функції.
Необмеженість цільової функції відповідно до ознаки 2 у таблиці 5.7 не виявлено.
5 етап: перевірка допустимості знайденого базисного рішення.
Знайдене базисне рішення відповідно до ознаки 3 допустиме, оскільки не містить негативних компонентів.
6 етап: перевірка оптимальності знайденого базового рішення.
Знайдене базисне рішення відповідно до ознаки 4 не оптимальне, оскільки у рядку цільової функції симплекс-таблиці (таблиця 5.7) міститься негативний елемент: –3 (вільне число цього рядка при розгляді даної ознаки не враховується). Отже, переходимо до 8 етапу.
8 етап: визначення роздільної здатності елемента.
8.1. Визначення роздільної здатності колонки.
Знайдене базисне рішення припустиме, визначаємо колонки з негативними елементами рядку цільової функції (крім колонки вільних чисел). Згідно з таблицею 5.7, такою колонкою є лише одна колонка: « х5». Отже, її приймаємо як дозволену.
8.2. Визначення роздільної здатності рядка.
Згідно з отриманими значеннями позитивних оціночних відносин у таблиці 5.8, мінімальним є відношення, що відповідає рядку « х4». Отже, її приймаємо як дозволену.
Таблиця 5.8
Симплекс-таблицяIII ітерації
Оціночні відносини |
||||
5/5 = 1 - min |
||||
9 етап: перетворення симплекс-таблиці.
Перетворення симплекс-таблиці (таблиці 5.8) виконуються аналогічно, як і попередньої ітерації. Результати перетворень елементів симплекс-таблиці наведено у таблиці 5.9.
IV ітерація
1 етап: побудова нової симплекс-таблиці.
За результатами симплекс-перетворень попередньої ітерації складаємо нову симплекс-таблицю:
Таблиця 5.9
Симплекс-таблицяIV ітерації
Оціночні відносини |
||||
| –(–3/5)=3/5 | |||
–(1/5)=–1/5 | ||||
| –(9/5)=–9/5 | |||
|
| –(–3/5)=3/5 |
2 етап: визначення базового рішення.
В результаті проведених симплекс-перетворень отримали нове базисне рішення, згідно з таблицею 5.9.
3 етап: перевірка сумісності системи обмежень.
Не сумісність системи обмежень відповідно до ознаки 1 у таблиці 5.9 не виявлено.
4 етап: перевірка обмеженості цільової функції.
Необмеженість цільової функції відповідно до ознаки 2 у таблиці 5.9 не виявлено.
5 етап: перевірка допустимості знайденого базисного рішення.
Знайдене базисне рішення відповідно до ознаки 3 допустиме, оскільки не містить негативних компонентів.
6 етап: перевірка оптимальності знайденого базового рішення.
Знайдене базисне рішення відповідно до ознаки 4 оптимальне, так як у рядку цільової функції симплекс-таблиці (таблиця 5.9) немає негативних елементів (вільне число даного рядка при розгляді цієї ознаки не враховується).
7 етап: перевірка альтернативності рішення.
Знайдене рішення є єдиним, оскільки у рядку цільової функції (таблиця 5.9) немає нульових елементів (вільне число цього рядка при розгляді цієї ознаки не враховується).
Відповідь: оптимальне значення цільової функції розглянутої задачі =24, яке досягається при.
Приклад 5.2.Вирішити наведене вище завдання лінійного програмування за умови, що цільова функція мінімізується:
Рішення:
I ітерація:
1 етап: формування вихідної симплекс-таблиці.
Вихідне завдання лінійного програмування поставлено у стандартній формі. Наведемо її до канонічного виду шляхом введення в кожне з обмежень-нерівностей додаткової невід'ємної змінної, тобто.
В отриманій системі рівнянь приймемо як дозволені (базисні) змінні х3, х4, х5, х6, тоді вільними змінними будуть х1,х2. Висловимо базисні змінні через вільні.
Розглянемо симплекс-методна вирішення завдань лінійного програмування (ЛП). Він заснований на переході від одного опорного плану до іншого, у якому значення цільової функції зростає.
Алгоритм симплекс-методу наступний:
- Вихідне завдання переводимо у канонічний вигляд шляхом запровадження додаткових змінних. Для нерівності виду ≤ додаткові змінні вводять зі знаком (+ ), якщо виду ≥ то зі знаком (— ). У цільову функцію додаткові змінні вводять із відповідними знаками з коефіцієнтом, що дорівнює 0 , т.к. цільова функція має при цьому змінювати свій економічний сенс.
- Виписують вектор P iз коефіцієнтів при змінних та стовпцях вільних членів. Цією дією визначається кількість одиничних векторів. Правило – одиничних векторів має бути стільки, скільки нерівностей у системі обмежень.
- Після цього вихідні дані вводяться в симплекс-таблицю. У базис вносяться поодинокі вектори, і виключаючи їх з базису, знаходять оптимальне рішення. Коефіцієнти цільової функції записують із протилежним знаком.
- Ознака оптимальності для завдання ЛП - рішення оптимальне, якщо в f- У рядку всі коефіцієнти позитивні. Правило знаходження роздільного стовпця – проглядається f- Рядок і серед її негативних елементів вибирається найменше. Вектор P iйого містить стає вирішальним. Правило вибору роздільної здатності – складаються відношення позитивних елементів роздільного стовпця до елементів вектора Р 0і те число, яке дає найменше ставлення стає роздільним елементом, щодо якого буде зроблено перерахунок симплекс-таблиці. Рядок, що містить цей елемент називається роздільною здатністю. Якщо в стовпці, що дозволяє, немає позитивних елементів, то завдання не має рішення. Після визначення роздільної здатності елемента переходять до перерахунку нової симплекс – таблиці.
- Правила заповнення нової симплекс - таблиці. На місці роздільного елемента проставляють одиницю, а інші елементи вважають рівними 0 . Дозволяючий вектор вносять у базис, з якого виключають відповідний нульовий вектор, інші базисні вектора записують без змін. Елементи роздільної здатності ділять на роздільний елемент, а інші елементи перераховують за правилом прямокутників.
- Так роблять до тих пір, поки в f- У рядку всі елементи не стануть позитивними.
Розглянемо розв'язання задачі з використанням розглянутого вище алгоритму.
Дано:
Наводимо завдання до канонічного вигляду:
Складаємо вектор:
Заповнюємо симплекс - таблицю:
:
Перерахуємо перший елемент вектора Р 0, Для чого складаємо прямокутник з чисел: і отримуємо: 
.
Аналогічні розрахунки виконаємо всім інших елементів симплекс – таблици:
В отриманому плані f– рядок містить один негативний елемент – (-5/3), вектора P 1. Він містить у своєму стовпці єдиний позитивний елемент, який буде роздільним елементом. Зробимо перерахунок таблиці щодо цього елемента:
Відсутність негативних елементів у f– рядку означає, що знайдено оптимальний план:
F * = 36/5, Х = (12/5, 14/5, 8, 0, 0).
- Ашманов З. А. Лінійне програмування, М: Наука, 1998г.,
- Вентцель Є.С. Дослідження операцій, М: Радянське радіо, 2001р.
- Кузнєцов Ю.М., Кузубов В.І., Волошенко О.Б. Математичне програмування, М: Вища школа, 1986р.
Рішення лінійного програмування на замовлення
Замовити будь-які завдання з цієї дисципліни можна на нашому сайті. Прикріпити файли та вказати терміни можна на
