1.Dirisha la Amri(Dirisha la amri).
Semi za hisabati zimeandikwa kwenye mstari wa amri baada ya " >> " haraka. Kwa mfano,
Ili kufanya kitendo, bonyeza kitufe cha "Ingiza".
Kwa chaguo-msingi, programu inaandika matokeo kwa ans maalum ya kutofautiana.
Ili kuhifadhi matokeo chini ya jina tofauti, tumia jina tofauti na ishara ya mgawo "=", kwa mfano
>> z = 1.25 /3.11
Hariri katika Dirisha la Amri Unaweza kutumia tu mstari wa amri wa sasa. Ili kuhariri amri iliyoingia hapo awali, unahitaji kuweka mshale kwenye mstari wa pembejeo na utumie vitufe "" au "".
Ikiwa amri inaisha na ";", basi matokeo ya hatua yake hayaonyeshwa kwenye mstari wa amri.
Dirisha la amri linaweza kufungwa na kifungo "", na kifungo "" kinatumikia kutenganisha dirisha kutoka kwa interface ya mfumo. Unaweza kurudi kwa fomu ya kawaida ya dirisha kwa kutumia menyu:
Menyu kuu → Eneo-kazi → Muundo wa Eneo-kazi → Chaguomsingi.
Unaweza kufuta dirisha la amri kwa kutumia menyu:
Menyu kuu → Hariri → Futa Dirisha la Amri.
Menyu kuu ya mfumo wa MatLab.
Menyu kuu MatLab ina vitu vifuatavyo:
Faili(Faili) - fanya kazi na faili;
Hariri(Hariri) - kuhariri;
Tazama(Angalia) - usimamizi wa dirisha;
Mtandao- mawasiliano na kampuni ya msanidi programu kupitia mtandao;
Dirisha(Dirisha) - uunganisho na madirisha ya mfumo;
Msaada(Msaada) - kiungo kwenye mfumo wa usaidizi MatLab.
Upau wa vidhibiti wa mfumo wa MATLAB.
Vifungo vya upau wa zana vina madhumuni yafuatayo:
Faili mpya(Mpya) - inaonyesha madirisha ya mhariri wa faili;
Fungua faili(Fungua) - inafungua madirisha ya kupakua faili;
Kata(Kata) - hupunguza kipande kilichochaguliwa na kuiweka kwenye ubao wa kunakili;
Nakili(Nakala) - nakala za kipande kilichochaguliwa kwenye ubao wa kunakili;
Bandika(Bandika) - huhamisha kipande kilichochaguliwa kutoka kwenye ubao wa clip hadi kwenye mstari wa pembejeo;
Tendua(Ghairi) - kufuta matokeo ya operesheni ya awali;
Rudia(Rudia) - kurudia matokeo ya operesheni ya awali;
Simulink- huunda mfano wa Simulink (viendelezi MatLab);
Dirisha la Msaada(Msaada) - hufungua madirisha ya usaidizi.
4. Umbizo la pato la matokeo ya hesabu .
Wakati wa kuingiza nambari halisi, nukta hutumiwa kutenganisha sehemu ya sehemu!
>> s = 0.3467819
Matokeo ya hesabu yanaonyeshwa katika muundo mfupi(nukuu fupi kwa nambari), ambayo inafafanuliwa kwa chaguo-msingi. Unaweza kubadilisha umbizo kuwa ndefu(nukuu ya nambari ndefu).
>> muundo mrefu
0.34678190000000
Kwenye orodha Umbizo la Nambari miundo ya nambari inapatikana
mfupi- nukuu fupi ya nambari;
ndefu- nukuu ya nambari ndefu;
mfupi e- nukuu fupi ya nambari katika muundo wa sehemu inayoelea;
ndefu e- rekodi ndefu ya nambari katika muundo wa sehemu inayoelea;
fupi g- fomu ya pili ya nukuu fupi ya nambari;
mrefu g- fomu ya pili ya nukuu ndefu ya nambari;
Umbizo la kuonyesha data ya nambari linaweza kuwekwa kwenye menyu Faili(faili) kipengee Mapendeleo(mapendeleo). Nenda kwenye kichupo Dirisha la Amri(dirisha la amri). Katika chaguo Onyesho la maandishi(onyesho la maandishi), katika orodha Umbizo la nambari(muundo wa nambari) seti fupi g, katika chaguo Onyesho la nambari(onyesha nambari) seti kompakt. Hizi towe hutengeneza nambari za pato katika umbo zima la tarakimu tano muhimu na kukandamiza nafasi nyeupe kati ya mistari.
Misingi ya mahesabu katika MatLab.
Kufanya shughuli rahisi za hesabu katika MatLab waendeshaji hutumiwa:
· kuongeza na kutoa +, – ;
· kuzidisha na kugawanya *, /;
· ufafanuzi ^ .
Baadhi ya vigezo maalum:
ans - matokeo ya operesheni ya mwisho bila ishara ya mgawo;
eps - makosa ya jamaa katika mahesabu ya hatua zinazoelea;
pi - nambari;
i au j - kitengo cha kufikiria;
Inf - infinity;
NaN - thamani isiyobainishwa.
Baadhi ya vipengele vya msingi vilivyojengwa ndaniMatLab:
exp(x) - kipeo cha nambari x;
logi (x) - logarithm ya asili ya nambari x;
sqrt (x) - mzizi wa mraba wa nambari x;
abs(x) - moduli ya nambari x;
sin(x), cos(x), tan(x), kitanda(x) - sine, kosine, tanjiti, cotangent ya nambari x;
asin(x), acos(x), atan(x), acot(x) - arcsine, arccosine, arctangent, arccotangent ya nambari x;
sec(x), csc(x) - secant, cosecant ya namba x;
round(x) - kuzungusha nambari x hadi nambari kamili iliyo karibu zaidi;
mod(x,y) - salio la mgawanyiko kamili wa x na y, kwa kuzingatia ishara;
ishara(x) - rudisha alama ya nambari x.
Wacha tuhesabu thamani ya usemi
![]()
>> exp(–2.5)*logi(11.3)^0.3 – sqrt((sin(2.45*pi)+cos(3.78*pi))/tan(3.3))
Ikiwa operator hawezi kuwekwa kwenye mstari mmoja, basi inawezekana kuendelea kuiingiza kwenye mstari unaofuata ikiwa unaonyesha ishara ya kuendelea "..." mwishoni mwa mstari wa kwanza, kwa mfano,
>> exp(–2.5)*logi(11.3)^0.3 - ...
sqrt((dhambi(2.45*pi)+cos(3.78*pi))/tan(3.3))
Kazi za kufanya kazi na nambari ngumu:
Inaingiza nambari changamano
>> z = 3 + 4i
3,0000 + 4.0000i
Vipengele vya kukokotoa abs(z), pembe(z) hurejesha moduli na hoja ya nambari changamano, ambapo , ;
complex(a,b) huunda nambari changamano kutoka kwa sehemu zake halisi na za kuwaziwa:
conj(z)hurejesha nambari changamano ya kuunganisha;
imag(z), real(z) hurejesha sehemu dhahania na halisi za nambari changamano z.
6. Vekta.
Kuingiza, kuongeza, kupunguza, kuzidisha kwa nambari.
Vekta ndani MatLab iliyoundwa kwa kutumia opereta mabano ya mraba. Katika kesi hii, vipengele vya vector ya safu vinatenganishwa na semicolon ";", na vipengele vya vector ya mstari vinatenganishwa na nafasi "" au comma ",".
Wacha tuanzishe vekta ya safu.
>> x =
Wacha tuanzishe vekta ya safu ![]() .
.
>> y =
Ili kubadilisha vekta, tumia apostrofi "'":
>> z = y'
Ili kupata jumla na tofauti ya vekta, tumia ishara "+" na "-":
>> c = x + z
Kuzidisha kwa vekta kwa nambari hufanywa kwa kulia na kushoto kwa kutumia ishara "*".
Vekta zinaweza kuwa hoja za kazi zilizojengewa ndani, k.m.
>> d = dhambi(c)
Kurejelea vitu vya vekta, mabano () hutumiwa, kwa mfano,
>> x_2 = x(2)
Kipengele cha mwisho cha vector kinaweza kuchaguliwa kwa kuandika amri
>> X_mwisho = x (mwisho)
Kutoka kwa vectors kadhaa unaweza kufanya moja, kwa mfano
>> r =
1.3 5.4 6.9 7.1 3.5 8.2
Herufi ya koloni " : " inatumika kutenganisha vipengele vingi kutoka kwa vekta, kwa mfano
>> w = r(3:5)
Tabia ya koloni " : " pia hukuruhusu kubadilisha vitu vya vekta, kwa mfano,
>> r(3:5)= 0
1.3 5.4 0 0 0 8.2
Ishara ":" pia inaweza kutumika kujenga vector, kila kipengele ambacho hutofautiana na uliopita kwa idadi ya mara kwa mara, i.e. hatua, kwa mfano
>> h =
1 1.2 1.4 1.6 1.8 2
Hatua inaweza kuwa mbaya (katika kesi hii, nambari ya kuanzia lazima iwe kubwa kuliko nambari ya mwisho).
Hatua sawa na moja inaweza kuachwa
>> k =
Kazi za msingi za kufanya kazi na vekta.
- urefu (x) - kuamua urefu wa vekta x;
- prod(x) - kuzidisha vipengele vyote vya vector x;
- jumla (x) - majumuisho ya vipengele vyote vya vector x;
- max (x) - kutafuta kipengele cha juu cha vector x;
- min(x) - kutafuta kipengele cha chini cha vekta x.
Ikiwa utaita kazi ya min au max na hoja mbili za pato = min(x),
basi variable ya kwanza inapewa thamani ya kipengele cha chini (kiwango cha juu), na kutofautiana kwa pili kunapewa nambari ya kipengele hiki.
7 Matrices.
Mbinu mbalimbali za kuingiza matrix.
1. Matrix inaweza kuingizwa kama vekta ya safu wima inayojumuisha vipengele viwili, ambavyo kila moja ni vekta ya safu mlalo na hutenganishwa na nusu koloni. Kwa mfano, hebu tuanzishe matrix
![]()
>> A =
2. Matrix inaweza kuingizwa mstari kwa mstari kwa kutekeleza mlolongo wa amri:
>> A =.
Algorithm inayotekelezwa katika \ operesheni ina hatua zifuatazo:
- 1. Katika kesi ndogo, ikiwa A ni ndogo na ya diagonal (sehemu ya Sparse Matrices imejitolea kwa matrices machache katika MATLAB), suluhisho linapatikana kwa kutumia formula rahisi x k = b k /a kk, ambapo k=1,2,. ..n.
- 3. Ikiwa A ni matrix ya juu au ya chini ya triangular, basi njia ya uingizaji wa inverse hutumiwa, au, ipasavyo, njia ya uingizwaji wa moja kwa moja, ambayo sehemu ya suluhisho hupatikana kutoka kwa mwisho (au equation ya kwanza) na kisha vipengele vilivyopatikana ni. imebadilishwa katika milinganyo ifuatayo ili kupata mifumo inayofuata ya vipengele vya suluhu ya milinganyo.
- 4. Ikiwa A - inaweza kupunguzwa kwa fomu ya pembetatu kwa vibali, basi upunguzaji unaolingana unafanywa, na kisha mfumo wa equations unatatuliwa kama katika hatua ya 3.
- 6. Ikiwa A ni matrix ya Hessenberg, basi inapunguzwa hadi tumbo la pembetatu ya juu (pamoja na marekebisho yanayolingana ya upande wa kulia) na kisha mfumo unatatuliwa kwa uingizwaji.
2. Ikiwa A ni mraba, nadra na matrix ya bendi, basi solver ya matrix ya bendi hutumiwa. Kunaweza kuwa na chaguzi mbili:
a. Ikiwa A ni matrix ya tridiagonal na b ni safu moja ya nambari halisi, basi mfumo unatatuliwa na uondoaji wa Gaussian (shughuli zake zinafanywa tu kwa vipengele kwenye diagonals). Ikiwa wakati wa mchakato wa kuondoa, ili kudumisha utulivu, ni muhimu kufanya vibali vya safu, au ikiwa tumbo A sio tridiagonal, basi hatua ifuatayo inafanya kazi.
b. Ikiwa A ni tepi yenye msongamano wa vipengele visivyo na sifuri zaidi ya parameter kupigwa marufuku, kwa chaguo-msingi sawa na 0.5, au masharti ya aya iliyotangulia hayajafikiwa, basi, kulingana na aina A na b ( mara mbili au single) taratibu zifuatazo za maktaba za LAPACK zinaitwa:
A na b ni maradufu halisi - taratibu DGBTRF, DGBTRS
A na b aina tata mara mbili - taratibu ZGBTRF, ZGBTRS
A au b aina halisi moja - taratibu SGBTRF, SGBTRS
A au b aina tata moja - taratibu CGBTRF, CGBTRS
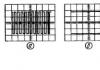
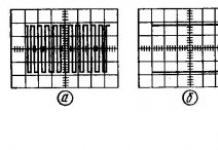
Uzito wa vitu visivyo na sifuri hueleweka kama uwiano wa idadi ya vitu visivyo na sifuri kwenye mkanda hadi idadi ya vitu vyote kwenye mkanda wa tumbo, kwa mfano, kwa matrix 7 hadi 7, templeti ambayo imepewa. chini, idadi ya vipengele visivyo na sifuri
nz = 1 (kwenye mchoro Na.-2) + 6 (kwenye mchoro Na.-1) + 7 (kwenye mchoro Na. 0) + 6 (kwenye mchoro Na. 1) + 1 (kwenye mchoro Na. 2) + 1 (kwenye mchoro Na. 3) = 22,
na idadi ya vipengele vyote kwenye mkanda
bendi = 5 (kwenye mchoro No.-2) + 6 (kwenye mchoro No.-1) + 7 (kwenye mchoro Na. 0) + 6 (kwenye mchoro Na. 1) + 5 (kwenye mchoro Na. 2) + 4 (kwenye mchoro Na. 3) = 33
na msongamano wa mambo yasiyo ya sifuri itakuwa 2/3. Tangu 2/3> 0.5, solver kwa matrices strip itatumika
Kigezo kupigwa marufuku, kama vigezo vingine vinavyodhibiti algoriti ndogo za matrix katika MATLAB, imewekwa kwa kutumia chaguo la kukokotoa la sparms.

Maana ya hatua hii ya algorithm ni kwamba kutatua mfumo na matrix ya mkanda hauhitaji vitendo nje ya mkanda. Ikiwa malisho yamejaa kabisa, basi hakutakuwa na vitendo vingi sana na vipengele vya sifuri. Kinyume chake, ikiwa mkanda ni mdogo sana, basi mbinu zilizotolewa katika hatua zaidi za algorithm zinaweza kuleta athari kubwa zaidi.
5. Ikiwa A ni matrix ya ulinganifu (au, katika kesi ngumu, Hermitian), na diagonal yake ina vipengele vyema vya kweli, basi kulingana na ikiwa A ni chache au la, kipengee a) au kipengee b) kinashikilia.
a. Ikiwa A sio chache, basi jaribio linafanywa kufanya utengano wa Cholesky A = R T R ikifuatiwa na mifumo ya kutatua yenye matrices ya triangular R T na R: R T y = b na Rx = y. Katika kesi hii, taratibu zifuatazo za maktaba ya LAPACK zinaitwa:
A na b ni halisi na mbili - DLANGE, DPOTRF, DPOTRS, DPOCON
A na b ni ngumu na mbili - ZLANGE, ZPOTRF, ZPOTRS, ZPOCON
A na b ni halisi na za aina moja - SLANGE, SPOTRF, SPOTRS, SDPOCON
A na b tata na aina moja - CLANGE, CPOTRF, CPOTRS, CPOCON
Mtengano wa Cholesky utashindwa ikiwa matrix sio chanya dhahiri. Lakini hakuna ukaguzi wa awali wa uhakika chanya, na imedhamiriwa kwa usahihi wakati wa mchakato wa mtengano, kwani mara nyingi inatosha kufanya hatua kadhaa za mtengano wa Cholesky ili kufafanua ukweli kwamba tumbo sio dhahiri (katika mchakato wa mahesabu inakuwa muhimu kutoa mzizi wa mraba wa nambari hasi). Ikiwa mtengano wa Cholesky haujaridhika, basi nenda kwenye hatua inayofuata.
b. Ikiwa A ni chache, basi vibali vya ulinganifu vya safu na nguzo hufanywa kwanza kwa kutumia algorithm ya kiwango cha chini cha ulinganifu (kazi symmmd) ili kupunguza kujazwa kwa sababu ya mtengano wa Cholesky, i.e. kupunguza idadi ya vitu vipya visivyo vya sifuri vinavyotokea wakati wa mchakato wa kujaza:
p = symmmd(A) - vekta p ina vibali
R = chol(A(p, p));
na mifumo miwili iliyo na vizidishio vya Cholesky inatatuliwa, ya kwanza ikiwa na kizidishio kilichopitishwa na vibali vinavyolingana katika vekta ya upande wa kulia.
na ya pili, na sababu ya upanuzi na kwa kuingiza vifaa vya suluhisho katika nafasi zinazolingana kwenye vekta x.
x(p, :) = R\y
7. Ikiwa A ni matrix ya mraba ambayo haikidhi masharti ya aya ya 1-6, basi kulingana na ikiwa ni chache au la, vitendo vifuatavyo vinafanywa.
a. Ikiwa A sio matrix ya nadra, basi kutumia uondoaji wa Gaussian na uchaguzi wa kitu kinachoongoza (kuhakikisha utulivu wa mtengano), mtengano wa LU wa matrix A = LU unafanywa, ambapo
U - tumbo la juu la triangular
L ni matriki iliyopunguzwa hadi pembetatu kwa vibali vya safu mlalo
na suluhisho la mfumo Ax = b hupatikana kwa mifumo ya kutatua sequentially na matrices ya triangular Ly = b, Ux = y.
Ili kufanya mtengano wa LU, taratibu zifuatazo za maktaba ya LAPACK huitwa:
A na b ni halisi na mbili - DLANGE, DGESV, DGECON
A na b ni ngumu na mbili - ZLANGE, ZGESV, ZGECON
A na b ni halisi na za aina moja - SLANGE, SGESV, SGECON
A na b ni changamano na aina moja - CLANGE, CGESV, CGECON
b. Ikiwa A ni matrix ya nadra, basi nguzo hupangwa upya ili kupunguza kujazwa kwa sababu za L na U katika mchakato wa kutafuta mtengano. Zaidi ya hayo, kwa kupanga upya safu katika mchakato wa mtengano wa LU, utulivu wa computational unahakikishwa, baada ya hapo mifumo yenye matrices ya triangular hutatuliwa tena. Kufanya mtengano wa LU wa matrix ya sparse, taratibu za maktaba ya UMFPACK hutumiwa
8. Ikiwa pointi za awali za algorithm hazikufanya kazi na, kwa hiyo, A sio matrix ya mraba, basi kila kitu kinatambuliwa na sparsity yake na moja ya pointi hapa chini inafanya kazi:
a. Ikiwa A sio matriki machache, basi mtengano wa QR AP = QR unafanywa, ambapo P ni matriki ya safu wima, Q ni tumbo la othogonal (Q T Q = I), na R ni ya pembetatu ya juu. Ikiwa A ni saizi m kwa n, basi Q ni saizi m kwa m, na R ni saizi ya m kwa n. Ifuatayo, suluhisho la mfumo linapatikana kama ifuatavyo:
x = P*(R \ (Q" * b))
kwani kutoka kwa Ax = b na AP = QR inafuata: QRx = bP na Rx = Q T bP.
b. Katika kesi ya matrix ya nadra na ya mstatili A, hakuna maana katika kuhesabu matrix Q, kwani itakuwa na uwezekano mkubwa wa kujazwa. Kwa hiyo, algorithm ya mtengano wa QR huhesabu c = Q T b (yaani, upande wa kulia uliobadilishwa) na kutatua mfumo Rx = c na tumbo la pembetatu ili kupata suluhisho kwa mfumo wa awali Ax = b.
Kwa kuongezea yote yaliyo hapo juu, algorithm hapo juu inatathmini hali ya matrix na kuonyesha onyo juu ya kosa linalowezekana katika suluhisho ikiwa tumbo halijawekwa vizuri (tazama sehemu ya Ushawishi wa hali ya matrix kwa usahihi. ya kutatua mfumo nayo). Algorithm iliyo hapo juu ina ukaguzi mbalimbali ambao unaweza kuchukua muda muhimu zaidi. Sehemu inayofuata, Kazi ya linsolve ya kutatua mifumo ya milinganyo ya mstari, inatanguliza kazi ya linsolve, ambayo hukuruhusu kubainisha aina ya matriki, na hivyo kupunguza muda wa kukokotoa.
linsolve kazi ya kutatua mifumo ya milinganyo ya mstari
Badala ya kutatua mfumo (au mifumo iliyo na pande nyingi za mkono wa kulia zilizofafanuliwa katika matrix) ya milinganyo ya aljebra ya mstari kwa kutumia ishara ya backslash, unaweza kutumia kazi ya linsolve, ambayo haifanyi ukaguzi wote wa matrix ulio katika \ algorithm ya operesheni ( tazama sehemu iliyotangulia).
Chaguo za kukokotoa za linsolve huitwa kwa umbo rahisi zaidi na hoja mbili za ingizo na hoja moja ya towe
x = suluhisha (A, b)
hutatua mfumo Ax = b kwa njia moja, kulingana na ikiwa matrix ni ya mraba au la.
- Ikiwa A ni tumbo la mraba, basi mtengano wake wa LU huhesabiwa kwanza na kisha mifumo miwili yenye matrices ya triangular L na U hutatuliwa.
- Ikiwa A ni matrix ya mstatili, basi mtengano wake wa QR huhesabiwa kwanza na kisha mfumo wenye matrices ya triangular hutatuliwa.
(Maelezo zaidi juu ya vitendo na sababu za upanuzi zinazosababishwa zimeandikwa katika sehemu). Zaidi ya hayo, ikiwa matriki A haina hali mbaya au A ni safu ya safu isiyo kamili, basi onyo linalolingana linaonyeshwa, kwa mfano:
A =; b =; x = linsolve(A,b) Onyo: Cheo kina upungufu, cheo = 1, tol = 4.4686e-015. x = 0 0 2.0000
Ili kukandamiza ujumbe huu kutoka kwa kuchapishwa kwenye dirisha la amri, piga kazi ya linsolve na hoja mbili za matokeo.
= suluhisha (A, b)
basi suluhisho linalotokana litaandikwa kwa x, na katika r - ama safu ya matrix (ikiwa A ni matrix ya mstatili), au usawa wa makadirio ya nambari ya hali yake (tazama sehemu), kwa mfano.
A =; b =; = linsolve(A,b) x = -1.0000e+000 9.9999e-001 3.3307e-006 r = 6.9444e-013
Faida kuu za kazi ya linsolve juu ya \ operesheni huonekana wakati wa kutaja aina ya matrix ya mfumo wa equations. Ili kufanya hivyo, kabla ya kupiga kazi ya linsolve, unahitaji kujaza muundo na habari kuhusu tumbo na sehemu zifuatazo.
- SYM - ulinganifu;
- LT - chini ya triangular;
- UT - juu ya triangular;
- UHESS - Hessenberg;
- POSDEF - ulinganifu, chanya uhakika;
- RECT - mstatili;
- TRANSA - ikiwa ni muhimu kutatua mfumo na matrix iliyopitishwa kwa moja iliyotolewa.
Kila sehemu inaweza kuwa ya kweli au ya uwongo. Kwa kweli, sio mchanganyiko wote wa maadili ya uwanja ni halali; kwa mfano, matrix haiwezi kuwa ya pembetatu na wakati huo huo linganifu na chanya dhahiri. Mchanganyiko sahihi wa maadili ya shamba hukusanywa katika jedwali lifuatalo
| LT | UT | UHESS | SYM | POSDEF | RECT | TRANSA |
| kweli | uongo | uongo | uongo | uongo | kweli/uongo | kweli/uongo |
| uongo | kweli | uongo | uongo | uongo | kweli/uongo | kweli/uongo |
| uongo | uongo | kweli | uongo | uongo | uongo | kweli/uongo |
| uongo | uongo | uongo | kweli | kweli | uongo | kweli/uongo |
| uongo | uongo | uongo | uongo | uongo | kweli/uongo | kweli/uongo |
Ikiwa matrix ya mfumo ni chanya dhahiri, basi hii lazima izingatiwe wakati wa kusuluhisha, kwani kwa matrices chanya, suluhisho linategemea mtengano wa Cholesky, ambao unahitaji shughuli chache kuliko mtengano wa LU unaotumiwa wakati wa kutatua mifumo iliyo na matiti ya jumla ya mraba. . Hii ni rahisi kudhibitisha kwa msaada wa mfano ufuatao, ambapo matrix ya uhakika ya ulinganifu huundwa (matrix ya nambari za nasibu huongezwa kwa kupitisha na idadi kubwa huongezwa kwa diagonal) na mfumo wa milinganyo na matriki hii hutambulishwa kwanza kama mfumo wenye matriki ya umbo la jumla (opts. SYM = uongo na opts.POSDEF = uongo), na kisha kama ilivyo kwa matrix ya uhakika na chanya (opts.SYM = true na opts). .POSDEF = kweli).
% imeweka sehemu zote za muundo wa ops, isipokuwa SYM na POSDEF opts.TRANSA = uongo; opts.UHESS = uongo; opts.RECT = uongo; opts.UT = uongo; opts.LT = uongo; % tengeneza vekta ya ukubwa wa matrix N = 2.^(8:12); % tengeneza safu tupu za kurekodi nyakati za suluhisho TimeGeneral = ; TimePosSym = ; % katika kitanzi tunaunda matrices na kulinganisha nyakati za ufumbuzi kwa n = N % tunaunda matrix ya uhakika na chanya % na vekta ya upande wa kulia A = rand(n); A = A + A" + 2*n*jicho(n); b = jumla(A, 2); % suluhisha mfumo kama mfumo wenye opts za jumla za matrix.SYM = sivyo; opts.POSDEF = uongo; Tstart = cputime; x = linsolve(A,b, opts); Tend = cputime; TimeGeneral = ; % suluhisha mfumo kama mfumo wenye opts za ulinganifu na nafasi.SYM = kweli; opts.POSDEF = kweli; Tstart = cputime; x = linsolve(A,b, opts); Tend = cputime; TimePosSym = ; mwisho % logi ya takwimu ya muda wa kuonyesha grafu(N, TimeGeneral, N, TimePosSym) lejend("TimeGeneral", "TimePosSym")
Gharama za hesabu za njia hizi za kutatua mfumo zinaonyeshwa kwenye grafu hapa chini

Kwa kweli, ikiwa matrix ni ya pembetatu, basi ni muhimu sana kuashiria hii, kwani kutatua mfumo na matrix ya pembetatu hufanywa katika shughuli za O (n 2), na ikiwa suluhisho la algorithm iliyoundwa kwa matrix. fomu ya jumla inatumika kwa mfumo na matrix ya pembe tatu, basi itachukua kuhusu O (n 3) shughuli.
Chaguo za kukokotoa za linsolve haziangalii ikiwa matriki inakidhi sifa zilizobainishwa, jambo ambalo linaweza kusababisha hitilafu. Kwa mfano, ikiwa, wakati wa kutatua mfumo na matrix ifuatayo na upande wa kulia
A =; b =; weka kweli kwa uga wa UT (na weka zingine zote kuwa za uwongo) opts.UT = kweli; opts.TRANSA = uongo; opts.LT = uongo; opts.UHESS = uongo; opts.SYM = uongo; opts.POSDEF = uongo; opts.RECT = uongo; basi wakati wa kusuluhisha mfumo, kazi ya linsolve itazingatia matrix kama pembetatu ya juu na kuchagua vitu vinavyohitaji kutoka kwa pembetatu ya juu A x = linsolve(A,b, opts) Hii itasababisha suluhisho x = 1 1 1 sambamba na tumbo A =;
Ushawishi wa hali ya tumbo juu ya usahihi wa kutatua mfumo nayo
Katika sehemu hii, tunaangalia jinsi makosa katika vipengele vya vekta ya upande wa kulia na katika tumbo la mfumo wa milinganyo ya mstari Ax = b inaweza kuathiri suluhisho la mfumo huo. Hebu kwanza tugeuke kwenye kesi ya kuanzisha usumbufu kwenye vector ya upande wa kulia b. Kwa hivyo tunatatua mifumo miwili
Zaidi ya hayo, inadhaniwa kuwa tunasuluhisha kila moja ya mifumo haswa, na swali kuu linalojitokeza ni jinsi suluhisho x la mfumo (1) litakuwa tofauti na suluhisho la mfumo (2) na usumbufu upande wa kulia δb. Hili ni swali muhimu sana, kwani vipengee vilivyo upande wa kulia vinaweza kupatikana kama matokeo ya vipimo vingine, mtawalia vyenye hitilafu δb k katika kila sehemu b k. Ningependa kwamba wakati wa kupima idadi sawa (kila wakati na makosa yake madogo), suluhisho zinazolingana za mifumo iliyo na pande tofauti za kulia pia hazitofautiani sana kutoka kwa kila mmoja. Kwa bahati mbaya, hii sio wakati wote. Sababu ya hii ni tabia ya matrix inayoitwa yake masharti. Hili litajadiliwa zaidi.
Kwanza, unahitaji kuanzisha kipimo cha ukaribu wa vectors na x, i.e. vekta ya makosa. Kipimo cha ukubwa wa vector ni kawaida (inaweza kuelezwa kwa njia tofauti). Kwa sasa, wacha tuchukue kama kawaida kawaida ya Euclidean ya vekta (mizizi ya mraba ya jumla ya miraba ya sehemu zake), i.e.

Ipasavyo

ambapo n ni idadi ya haijulikani na milinganyo katika mfumo. Mbali na kawaida ya vekta kukadiria ukubwa wa vekta, tunahitaji pia kawaida ya tumbo ili kukadiria ukubwa wa matrix. Wacha tuchukue kawaida ya matrix, ambayo inafafanuliwa kama ifuatavyo (inaitwa kawaida ya spectral):
![]()
hizo. kawaida ya matrix ya spectral ni sawa na mzizi wa mraba wa eigenvalue ya juu ya matrix A T A. MATLAB ina kazi ya kawaida ya kuhesabu kanuni za matrices na vectors, ambayo, hasa, inaweza kuhesabu kanuni zilizo hapo juu. Kwa nini tulichagua kanuni hizi maalum za vectors na matrices inaelezwa kwa undani katika sehemu, ambapo mahesabu machache na ufafanuzi hutolewa. Hii inahusiana na makadirio ambayo tutatumia kwa hitilafu katika kutatua mfumo (upatikanaji wa usawa huu pia umetolewa katika sehemu iliyotajwa):

Hapa tunaashiria nambari ya hali ya matrix, ambayo inafafanuliwa kama ifuatavyo.
![]()
Kutoka kwa usawa hapo juu inafuata kwamba idadi kubwa ya hali ya matrix ya mfumo, kosa kubwa la jamaa katika suluhisho linaweza kuwa na kosa ndogo upande wa kulia.
Wacha tuchunguze mfano wa kawaida wa tumbo lisilo na hali mbaya - tumbo la Hilbert - na tujue jinsi kosa lililo upande wa kulia wa mfumo huathiri kosa katika suluhisho. Matrix ya Hilbert imefafanuliwa kama ifuatavyo

Ili kuunda matrix ya Hilbert, MATLAB hutoa kazi ya hilb, ambayo hoja yake ya ingizo hubainisha saizi ya matrix. Wacha tuchukue matrix ndogo 6 kwa 6:
N = 6; H = hilb(n) H = 1.0000 0.5000 0.3333 0.2500 0.2000 0.1667 0.5000 0.3333 0.2500 0.2000 0.1667 0.1667 0.1667 0.14350 0.14350 0.300 ... 0.1000 0.0909
X = ndio(n, 1); b = H*x b = 2.4500 1.5929 1.2179 0.9956 0.8456 0.7365
Tunaona kuwa hakuna kitu "cha kutiliwa shaka" katika matrix au vekta iliyo upande wa kulia; nambari zote sio tofauti sana kutoka kwa kila mmoja. Sasa hebu tuunde upande wa kulia uliovurugika wa b + δb kwa kuongeza nambari ndogo za mpangilio wa 10 -5 kwenye vekta b na tusuluhishe mfumo kwa upande wa kulia ulioyumba ili kupata vekta .
Delta_b = 1e-5*(1:n)"; x_tilda = H\(b + delta_b) x_tilda = 0.9978 1.0735 0.4288 2.6632 -1.0160 1.8593
Inaweza kuonekana kuwa suluhisho linalotokana ni mbali na moja halisi, ambapo vitengo vyote vinapaswa kuwa. Wacha tuhesabu kosa la jamaa katika suluhisho na upande wa kulia (kazi ya kawaida kwa chaguo-msingi huhesabu kawaida ya Euclidean ya vekta):
Delta_x = x - x_tilda; KUSHOTO = kawaida(delta_x)/kawaida(x) KUSHOTO = 1.1475 KULIA = kawaida(delta_b)/kawaida(b) KULIA = 2.7231e-005
Kwa hivyo, kosa katika suluhisho ni la mpangilio wa umoja, ingawa mabadiliko ya upande wa kulia yalikuwa ya mpangilio wa 10 -5. Hii inalingana kikamilifu na ukosefu wa usawa hapo juu kwa makosa. Kwa kweli, wacha tuhesabu nambari ya hali cond(H) kwa kutumia kitendakazi cha MATLAB kinachoitwa cond na kwa chaguo-msingi mahesabu. ![]() kwa kawaida ya spectral ya matrix
kwa kawaida ya spectral ya matrix
C = cond(H) c = 1.4951e+007
KUSHOTO ≈ 1.1475 kidogo
C* HAKI? 1.4951e+07 * 2.7231e-05 ≈ 407
na ukosefu wa usawa umeridhika (hata kwa kiasi fulani).
Wakati ukubwa wa tumbo la Hilbert unavyoongezeka, kosa katika suluhisho litaongezeka tu (hii ni rahisi kuangalia kwa kuweka n = 7, 8, ...). Kwa kuongezea, kwa n = 12 ujumbe utaonyeshwa ukisema kuwa tumbo halina hali mbaya na suluhisho linaweza kuwa sio sahihi.
Onyo: Matrix iko karibu na umoja au mizani mbaya.
Matokeo yanaweza kuwa si sahihi. RCAND = 2.409320e-017.
Kama kipimo cha masharti, thamani iliyochaguliwa hapa ni RCOND sawa na ile iliyogawanywa na makadirio ya nambari ya hali (nambari ya hali inakadiriwa kwa kutumia algoriti ya haraka sana ambayo inafanya kazi haraka sana kuliko cond, ambayo imeelezewa kwa undani zaidi katika usaidizi. kwenye kazi ya rcond). Ikiwa thamani ya RCOND ni ndogo, basi matrix inachukuliwa kuwa haina hali mbaya.
Kuongezeka kwa makosa katika suluhisho kadiri saizi ya matrix ya Hilbert inavyoongezeka ni kwa sababu ya ukweli kwamba nambari ya hali ya matrix ya Hilbert inakua haraka sana na saizi yake. Hii ni rahisi kuthibitisha kwa kutumia kitanzi rahisi na kazi ya semilojia (kipimo kando ya mhimili wa kuratibu ni wa logarithmic):
N = 1:20; C = sufuri (1, 20); kwa n = N H = hilb(n); C(n) = cond(H); semilojia ya mwisho(N, C) imewashwa, kichwa("cond(H)"), xlabel("n")

Kwa njia, kwa kuwa kazi ya cond hupata nambari ya hali kwa kutumia njia ya nambari (yaani, upanuzi wa umoja wa kupata nambari za umoja), nambari ya hali baada ya n = 12 haijahesabiwa tena kwa usahihi; kwa kweli, inapaswa kukua zaidi, ambayo inaweza. ithibitishwe kwa kutumia hesabu za ishara katika MATLAB na utendakazi na idadi fulani ya takwimu muhimu
N = 1:20; C = sufuri(1, N); tarakimu(60) kwa n = N H = vpa(sym(hilb(n)))); % hesabu ya matrix ya Hilbert sahihi kwa tarakimu ya 60 sigma = svd(H); % kupata thamani za umoja za matrix ya Hilbert % inayokokotoa nambari ya hali ya matrix ya Hilbert C(n) = max(double(sigma))/min(double(sigma)); semilojia ya mwisho(N, C) imewashwa, kichwa("cond(H)"), xlabel("n")

Acheni sasa tuchunguze mambo matatu muhimu kuhusu mfano huu.
Ya kwanza yao - kutatua mfumo Hx = b (na vekta ya upande wa kulia inayolingana na suluhisho kutoka kwa vitengo) kwa kutumia opereta wa nyuma hautatoa vitengo kamili, kosa litakuwa tayari kwenye nambari ya kumi (ingawa katika MATLAB yote. mahesabu hufanywa kwa usahihi maradufu kwa chaguo-msingi)
Umbizo la urefu wa H\b ans = 0.9999999999916 1.00000000002391 0.99999999983793 1.00000000042209 0.999999999530008 30008
Hii hutokea kwa sababu wakati wa kuhesabu vekta b wakati wa kuzidisha matrix H na vekta ya zote, tayari tumejumuisha makosa fulani ndani yake. Kwa kuongezea, makosa ya kuzunguka katika mchakato wa kutatua mfumo pia yalicheza jukumu na hali duni ya matrix (hata ya saizi ndogo) ilisababisha makosa kama hayo katika suluhisho. Hakika, kwa matrices ndogo na idadi ndogo ya hali, athari hiyo haitazingatiwa. Wacha tuchukue matrix 6 kwa 6 ya nambari za nasibu na tuhesabu nambari ya hali yake
A = rand(n); cond(A) ans = 57.35245279907571
Kisha tunaunda upande wa kulia unaofanana na suluhisho halisi kutoka kwa vitengo vyote
X = ndio(n, 1); b = A*x;
na kutatua mfumo, na kusababisha usahihi mzuri
>> A\b ans = 1.0000000000000 1.000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000Jambo la pili muhimu linahusiana na kiamua cha tumbo. Hebu tuhesabu kibainishi cha matrix ya 6 kwa 6 ya Hilbert ambayo kwayo tulitatua mfumo
>> det(hilb(6)) ans = 5.3673e-018Kiashiria kinageuka kuwa kidogo cha kutosha, ambacho mtu anaweza kufanya hitimisho lisilo sahihi kwamba chanzo cha tatizo la kosa kubwa katika suluhisho na usumbufu mdogo wa upande wa kulia wa mfumo ni udogo wa kiashiria. Kwa ukweli, hii sivyo; ikiwa kiashiria cha mfumo ni kidogo, hii haimaanishi kuwa matrix ina hali mbaya na, kwa hivyo, kuna kosa kubwa katika suluhisho. Kwa kweli, wacha tuchukue matrix
A =;
Kiamuzi chake ni kidogo sana, karibu 10 -121
Det(A) ans = 9.9970e-121
(neno "sana" bila shaka ni la masharti, lakini ni ndogo kuliko kiashiria cha tumbo la 6 kwa 6 la Hilbert, ambalo tulikuwa na matatizo wakati wa kutatua mfumo). Walakini, udogo wa kiashiria hautaathiri kwa njia yoyote kosa katika suluhisho wakati upande wa kulia wa mfumo unafadhaika, ambayo ni rahisi kuonyesha kwa kuunda mfumo na suluhisho inayojulikana, kuanzisha usumbufu katika upande wa kulia na kutatua. mfumo:
X = ; b = A*x; delta_b = 1e-5*; x_tilda = A\(b+delta_b); delta_x = x - x_tilda; KUSHOTO = kawaida(delta_x)/kawaida(x) KULIA = kawaida(delta_b)/kawaida(b) KUSHOTO = 2.1272e-005 KULIA = 2.1179e-005
Kwa hivyo, kosa la jamaa katika suluhisho ni karibu sawa na kosa la jamaa upande wa kulia, kwani nambari ya hali ya matrix A hapo juu ni kubwa kidogo kuliko 1, ambayo ni:
C = cond(A) c = 1.0303
Na hatimaye, fikiria swali la tatu kuhusu kufikia ishara sawa katika kukosekana kwa usawa kwa kosa katika suluhisho

Hiyo ni, kwa maneno mengine, hebu tujue: kunaweza kuwa na hali wakati tunafanya usumbufu mdogo wa upande wa kulia wa mfumo, sema 10 -5, nambari ya hali ya matrix ya mfumo ni sawa na 10 10. , na katika suluhisho kosa la jamaa la 10 5 linapatikana. Unaweza kupitia mifano mingi, ukijaribu matiti tofauti, usifikie usawa, na uhitimishe kimakosa kuwa hii ni makisio tu kutoka juu kwa kosa katika suluhisho. Walakini, hii sivyo, kwani mfano ufuatao unatushawishi.
ambayo usumbufu wa jamaa wa upande wa kulia ni 10 -5
KULIA = kawaida(delta_b)/kawaida(b) HAKI = 1.0000e-005
Hitilafu ya jamaa katika kutatua mfumo inageuka kuwa 10 5
X = A\b; x_tilda = A\(b+delta_b); delta_x = x - x_tilda; KUSHOTO = kawaida(delta_x)/kawaida(x) KUSHOTO = 1.0000e+005
Na hii hutokea kwa sababu
1) katika mfano huu, nambari ya hali ya matrix A ni 10 10;
C = cond(A) c = 1.0000e+010
2) kukosekana kwa usawa kwa kosa katika suluhisho hubadilika kuwa usawa.
Ikiwa tunaweka umbizo kwa muda mrefu, tunaona kwamba KUSHOTO, KULIA na nambari ya hali sio hasa 10 5 , 10 -5 na 10 10 , kwa mtiririko huo, lakini hii ni kutokana na makosa ya kuzunguka. Ikiwa itatatuliwa katika hesabu kamili, usawa utakuwa sawa, ambao unaweza kuonyeshwa kwa uchanganuzi (angalia sehemu).
Katika mifano iliyopita, tulidhani kuwa matrix haina makosa, na makosa yanaweza tu kuwa upande wa kulia wa mfumo wa milinganyo ya mstari. Katika mazoezi, inaweza kugeuka kuwa vipengele vya matrix ya mfumo vinatajwa na makosa, i.e. badala ya mfumo
| Shoka | V = || b || V ⇒ || A | M || x | V ≥ || b || V
wapi || | M ni kawaida ya matrix. Ili kufanya hivyo, kawaida ya matrix || | M na kawaida ya vekta || | V lazima itimize ukosefu wa usawa ufuatao
| A | M || x | V ≥ || Shoka | V
kwa matrices yoyote A na vekta x. Ikiwa ukosefu huu wa usawa unashikilia, basi kawaida ya matrix || | M inaitwa yaliyokubaliwa na kawaida ya vekta || | V. Inajulikana, kwa mfano, kwamba kawaida ya spectral
![]()
(mizizi ya mraba ya eigenvalue ya juu zaidi ya matrix A T) inalingana na kawaida ya vekta ya Euclidean

Ndiyo maana katika sehemu hii tulifanya majaribio yote kwa kutumia kanuni hizi.
Baada ya kupokea ukosefu wa usawa || A | M || x | V ≥ || b || V zaidi kumbuka kuwa kutoka kwa Ax = b inafuata kwamba . Kwa kuwa tumbo A si la umoja, inafuata kwamba δx = A -1 δb na || δx | V = || A -1 δb | V. Tena tunatumia uthabiti wa kanuni na kupata usawa || δx | V ≤ || A -1 | M || δb | V. Zaidi ya hayo, katika usawa mbili zilizopatikana
| A | M || x | V ≥ || b || V na || δx | V ≤ || A -1 | M || δb | V
Tunagawanya thamani ndogo ya moja ya kutofautiana kwa thamani kubwa ya usawa mwingine, na thamani kubwa, kwa mtiririko huo, na ndogo.

na kwa mageuzi rahisi hatimaye tunapata ukosefu wa usawa unaohitajika

wapi cond(A) = || A | M* || A -1 | M.
Kumbuka kwamba wakati wa kupata usawa kwa kosa, tulitumia ukweli tu kwamba kawaida ya matrix inaambatana na kawaida ya vekta. Hii ni kweli sio tu kwa kawaida ya spectral ya matrix na kawaida ya Euclidean ya vector, lakini pia kwa kanuni nyingine. Kwa hiyo, kwa mfano, kiwango cha juu cha kawaida cha matrix ya safu, iliyohesabiwa na formula

sambamba na kawaida ya vector ya kwanza
na kanuni ya juu zaidi ya safu mlalo ya matrix, inayokokotolewa na fomula

sambamba na kawaida ya vekta isiyo na kikomo
![]()
Kazi ya kawaida huhesabu sio tu kawaida ya Euclidean ya vekta na kawaida ya spectral ya matrix, lakini pia kanuni za vekta na matrix zilizoorodheshwa hapo juu. Ili kufanya hivyo, unahitaji kuiita na hoja ya pili ya ziada:
- q = kawaida(A, 1) - kiwango cha juu zaidi cha safu wima ya matrix A
- q = kawaida(A, inf) - kiwango cha juu cha safu mlalo ya matrix A
- q = kawaida (a, 1) - kawaida ya vekta ya kwanza ya a
- q = kawaida (a, inf) - kawaida ya vekta isiyo na kipimo a
Nambari ya hali ya matrix cond(A) = || A | M* || A -1 | M kwa heshima na kanuni mbalimbali za matrix inaweza kuhesabiwa kwa kutumia kazi ya cond. Ikiwa cond inaitwa kwa hoja moja ya pembejeo (matrix), basi nambari ya hali huhesabiwa kulingana na kawaida ya matrix ya spectral. Kupigia simu kitendakazi cha cond na hoja ya ziada hurejesha nambari za hali zinazohusiana na kawaida ya matrix iliyobainishwa:
- c = cond (A, 1) - nambari ya hali inayohusiana na kiwango cha juu cha kawaida cha safu ya matrix
- с = cond(A, inf) - nambari ya hali inayohusiana na kawaida ya safu ya juu ya matrix
Kama mfano unaoonyesha umuhimu wa uthabiti wa kawaida ya matriki na kawaida ya vekta katika ukosefu wa usawa wa hitilafu, tunatoa mfano na tumbo A, vekta ya upande wa kulia b na vekta ya hitilafu upande wa kulia wa delta_b.
A =; b = [ -5.7373057243726833e-001 -1.5400413072907607e-001 -5.3347697688693385e-001 -6.0209490373259589;-001] delta_b = [-0.71685839091451e-5 0.54786619630709e-5 0.37746931527138e-5 0.20850322383081e-5];
Wacha tuhesabu sehemu za kulia na kushoto za makadirio kwa kutumia kawaida ya vekta ya kwanza, na nambari ya hali ya matrix kuhusiana na kawaida ya matrix ya spectral.
KULIA = kawaida(delta_b,1)/kawaida(b,1); c = cond(A); x = A\b; x_tilda = A\(b+delta_b); delta_x = x - x_tilda; KUSHOTO = kawaida(delta_x,1)/kawaida(x,1); umbizo fupi e disp()
Tunapata maadili yafuatayo kwa pande za kushoto na kulia za usawa
9.9484e+004 9.9323e+004
Upande wa kushoto haupaswi kuzidi kulia (kama ilivyothibitishwa hapo juu), lakini ikawa kubwa zaidi kwa sababu ya uchaguzi wa kanuni zisizo sawa.
Hebu sasa tuchunguze kwa nini nambari ya hali ya matrix haiwezi kuwa chini ya moja. Nambari ya hali ya matrix A inafafanuliwa kama cond(A) = || A | M* || A -1 | M , wapi || A | M ni baadhi ya kawaida ya matrix ya A. Kawaida ya matrix (yaani kanuni ambayo nambari inahusishwa na kila matrix) haiwezi kuwa ya kiholela; lazima itimize mihimili minne ifuatayo:
A1. | A | ≥ 0 kwa matrix yoyote A na || A | = 0 ikiwa na tu ikiwa A ni matrix sifuri.
A2. | AA | = | α | *|| A | kwa matrix yoyote A na nambari α.
A3. | A + B || ≤ | A | + || B || kwa matrices yoyote A na B
A4. | AB | ≤ | A | *|| B || kwa matrices yoyote A na B.
Kutoka kwa axiom ya mwisho ni wazi kwamba kawaida hufafanuliwa tu kwa matrices ya mraba (ingawa katika fomula zilizo hapo juu za kuhesabu kanuni mbalimbali, kwa kanuni, hakuna kizuizi hicho). Kwa kuongezea, kutoka kwa axiom ya mwisho inafuata kwamba kawaida yoyote ya matrix ya kitambulisho sio chini ya moja, kwa kweli.
| Mimi | =|| Mimi*Mimi | ≤ | Mimi | 2 | Mimi | ≥ 1.
Halafu, tena kwa kutumia axiom ya nne, tunaona kuwa nambari ya hali ya matrix daima ni kubwa kuliko moja (kweli kwa nambari ya hali ya matrix kwa heshima na kawaida ya matrix ya kiholela)
1 ≤ | Mimi | =|| AA -1 | ≤ | A | *|| A -1 | = cond(A).
Wacha tukamilishe sehemu hii kwa kuchunguza sababu ya kuonekana kwa usawa kamili katika makadirio ya kosa katika suluhisho wakati upande wa kulia unafadhaika:

na kujenga mifano inayolingana katika MATLAB. (Majadiliano hapa chini yamo, kwa mfano, katika kitabu cha J. Forsythe, K. Mohler. Suluhu la nambari la mifumo ya milinganyo ya aljebra ya mstari. M: “Mir”, 1969.)
Jukumu muhimu katika hoja linachezwa na nadharia juu ya mtengano wa umoja wa matrix, kulingana na ambayo kwa matrix yoyote ya ukubwa wa n kuna matawi mawili ya orthogonal U na V ya saizi n kwa n (U T U = UU T na V T V = VV T) kiasi kwamba bidhaa D = U T AV ni matrix ya diagonal, na tunaweza kuchagua U na V ili

ambapo μ 1 ≥ μ 2 ≥…≥μ r ≥ μ r+1 =…=μ n =0,
na r ni daraja la matrix A. Nambari μ k zinaitwa nambari za spectral za matrix A. Kwa matrix isiyo ya umoja A, ifuatayo ni kweli:
μ 1 ≥ μ 2 ≥ … ≥μ n ≥ 0.
Jambo muhimu linalofuata ni kwamba kuzidisha kwa matrix ya orthogonal haibadilishi kawaida ya Euclidean ya vector, i.e. kwa vekta yoyote ya x iliyo na vipengee vya n na matrix yoyote ya orthogonal U ya saizi n kwa n usawa ni kweli
| Ux | =|| x |.
Kwa kuwa kuzidisha kwa matrix ya orthogonal haibadilishi kawaida ya spectral, basi
kwa hivyo, kwa nambari ya hali ya matrix usawa ufuatao ni kweli:
![]()
Tuna mifumo miwili: Ax = b (iliyo na suluhisho halisi x) na (yenye suluhisho kamili). Ni wazi, hitilafu δx ni suluhu kwa mfumo ambao upande wake wa kulia ni usumbufu δb, i.e. mifumo Aδx = δb. Hebu D = U T AV iwe mtengano wa thamani ya umoja wa matrix A, kisha UDV T = A kutokana na ukweli kwamba U na V ni matrices ya orthogonal. Zaidi
Shoka = b ⇒ UDV T x = b.
Wacha tuanzishe nukuu
x" = V T x, b" = U T b,
basi mifumo ifuatayo ni sawa
Shoka = b ⇔ Dx" = b"
Kwa njia sawa kabisa, fikiria mfumo kwa heshima na kosa
Aδx = δb ⇒ UDV T δx = δb
Tunatanguliza nukuu
δx" = V T δx, δb" = U T δb,
ambayo mifumo ifuatayo inageuka kuwa sawa
Aδx = δb ⇔ Dδx" = δb"
Wale. tumepata mifumo rahisi sawa na matrix ya diagonal, kwenye diagonal ambayo ni nambari za spectral za matrix A.
Hebu sasa tuchague pande za kulia za mifumo hii kwa njia maalum, yaani, basi
ambapo β > 0, basi suluhisho sambamba na mfumo Dx" = b" litakuwa
ambapo μ 1 ndio thamani ya juu ya umoja ya matrix A. Tutafanya vivyo hivyo na mfumo Dδx" = δ b", yaani, let
ambapo γ > 0, basi suluhisho linalolingana na mfumo Dδx" = δb" litakuwa

Kutoka kwa uhifadhi wa kawaida wa vekta wakati inazidishwa na matrix ya orthogonal, inafuata kwamba
β/μ 1 = || x" || = || V T x || = || x || na γ/μ n = || δx" || =|| V T δx | = ||δx ||.
Kwa njia ile ile tunapata usawa:
β = || b" || = || U T b || = || b || na γ = || δb" || =|| U T δb | =|| δb |

![]()
na tangu
![]()
basi hatimaye tunapata
![]()
Kwa hivyo, kwa kila tumbo A inawezekana kujenga vector upande wa kulia wa mfumo na usumbufu wake ili kwamba hitilafu katika suluhisho itakuwa bidhaa ya nambari ya hali ya matrix na kosa upande wa kulia. Katika MATLAB, ujenzi unaolingana unaweza kufanywa bila kutumia mtengano wa thamani ya umoja (ingawa inaweza kupatikana kwa kutumia kazi ya svd).
Kwanza tunaweka n na kupata matiti mbili za orthogonal U na V kwa kufanya mtengano wa QR wa n na n matrices kutoka kwa nambari za nasibu:
N = 4; = qr(rand(n)); = qr(rand(n));
D = diag();
Baada ya hayo, tunaunda matrix A kwa kutumia matrix ya diagonal D na matrices ya orthogonal U na V.
A = U*D*V";
Nambari ya hali ya matrix A itaambatana na nambari ya hali ya matrix D, ambayo kwa mfano wetu ni sawa na 10 10.
Beta = 1; gamma = 1e-5;
na ujenge vekta b" na δb"
B1 = "; db1 = ";
kutoka ambayo tunapata vekta b na δb
X = A\b; x_tilda = A\(b+db);
hesabu pande za kushoto na kulia za usawa
dx = x - x_tilda; HAKI = kawaida(db)/kawaida(b); KUSHOTO = kawaida(dx)/kawaida(x);na kuwatoa nje
Fomati fupi e disp()
Tunapata usawa
Lugha ya programu ya kutafsiri ya mfumo wa MATLAB imeundwa kwa njia ambayo mahesabu yoyote (wakati mwingine ngumu sana) yanaweza kufanywa kwa hali ya hesabu ya moja kwa moja, yaani, bila mtumiaji kuandaa programu. Katika kesi hii, MATLAB hufanya kazi za supercalculator na inafanya kazi katika hali ya mstari wa amri.
Kufanya kazi na mfumo ni mwingiliano wa asili na hufuata sheria "uliza swali na upokee jibu." Mtumiaji huandika usemi uliohesabiwa kwenye kibodi, huihariri (ikiwa ni lazima) kwenye mstari wa amri, na anakamilisha ingizo kwa kubonyeza kitufe cha ENTER. Kwa mfano, takwimu inaonyesha mahesabu rahisi na dhahiri kabisa.
Hata kutoka kwa mifano rahisi kama hii, hitimisho la kufundisha linaweza kutolewa:
* ili kuonyesha pembejeo ya data ya awali, ishara >> hutumiwa;
* data imeingizwa kwa kutumia mhariri rahisi wa mstari;
* kuzuia pato la matokeo ya hesabu ya usemi fulani, unahitaji kuweka ishara baada yake; (semicolon);
* ikiwa kigezo hakijabainishwa kwa thamani ya matokeo ya hesabu, basi MATLAB inapeana kigezo kama hicho kinachoitwa ans;
* ishara ya mgawo ni ishara sawa =, inayojulikana kwa wanahisabati, na sio ishara iliyojumuishwa: =, kama ilivyo katika lugha zingine nyingi za programu na mifumo ya hesabu;
* kazi zilizojengwa (kwa mfano, dhambi) zimeandikwa kwa herufi ndogo, na hoja zao zinaonyeshwa kwenye mabano;
* matokeo ya mahesabu yanaonyeshwa kwenye mistari ya pato (bila ishara >>);
* mazungumzo hufanyika kwa mtindo wa "aliuliza swali - alipokea jibu."
Mifano ifuatayo inaonyesha matumizi ya MATLAB kufanya idadi ya shughuli nyingine rahisi za vekta. Takwimu pia inaonyesha dirisha la kivinjari la mfumo wa faili, ambalo linapatikana kwenye kichupo cha Saraka ya Sasa. Katika hali ya amri, ni rahisi zaidi kuita dirisha la kivinjari cha mfumo wa faili kutoka kwa upau wa vidhibiti kwa kuwasha kitufe baada ya orodha ya saraka za mfumo wa MATLAB. Kunaweza kuwa na matukio ambapo mahesabu yameachwa ikiwa saraka ya sasa imewekwa vibaya, ikiwa faili za m zinazohitajika kwa hesabu hazijagunduliwa.
Katika mifumo mingi ya hisabati, kukokotoa sin(V) au exp(V), ambapo V ni vekta, kunaweza kutoa hitilafu kwa sababu kazi za kukokotoa dhambi na exp lazima ziwe na hoja kubwa. Hata hivyo, MATLAB ni mfumo wa matrix, na vekta ni aina ya matrix yenye ukubwa wa 1xn au n×1. Kwa hiyo, kwa upande wetu, matokeo ya hesabu yatakuwa vector ya ukubwa sawa na hoja V, lakini vipengele vya vector iliyorejeshwa itakuwa sines au vielelezo vya vipengele vya vector V.
Matrix imeainishwa kama safu ya vekta zinazowakilisha safu zake, zilizofungwa kwenye mabano ya mraba. Nafasi au koma hutumiwa kutenganisha vipengele vya vekta, na semicolon hutumiwa kutenganisha vekta moja kutoka kwa nyingine. Ili kuchagua kipengele cha mtu binafsi cha matrix M, usemi wa fomu M(j,i) hutumiwa, ambapo M ni jina la matrix, j ni nambari ya safu na i ni nambari ya safu.
Ili kutazama yaliyomo kwenye safu, ni rahisi kutumia kivinjari cha Workspace. Kila vekta na tumbo ndani yake huwakilishwa kama mraba na seli, upande wa kulia ambao saizi ya safu imeonyeshwa. Kubofya mara mbili kwenye mraba na panya husababisha kuonekana kwa dirisha la Mhariri wa Array. Kufanya kazi na mhariri wa safu ni dhahiri kabisa - huwezi kutazama tu vipengele vya safu, lakini pia kuhariri na kuchukua nafasi yao.
Kama inavyoonekana kutoka kwa mifano iliyotolewa, ingizo la misemo ya awali kwa hesabu katika mfumo wa MATLAB hufanywa katika umbizo la maandishi la kawaida. Matokeo ya hesabu, isipokuwa yale ya picha, yanaonyeshwa kwa muundo sawa. Hapa kuna mifano ya kurekodi mahesabu yaliyofanywa na MATLAB kwenye mstari wa amri:
Kufanya kazi na mhariri wa safu
Ili kuanza, chagua "Msaada wa MATLAB" kwenye menyu ya Usaidizi.
>> aina dhambi
dhambi ni kazi iliyojengeka ndani.
>> kusaidia dhambi
SIN(X) ni sine ya elementi za X.
Mbinu zilizojaa kupita kiasi
>>V=
0.8415 0.9093 0.1411 -0.7568
Hitilafu ya kutumia ==> ^
Matrix lazima iwe mraba.
Unaweza kuzingatia fomu ya majibu wakati wa kufanya shughuli rahisi bila kutaja tofauti ambayo matokeo yamepewa. Katika hali kama hizi, MATLAB yenyewe inapeana kutofautisha, ans, ambayo matokeo hupewa na thamani ambayo huonyeshwa.
Fomu ya pato na mapumziko ya mstari katika kipindi
Ikumbukwe sifa za pato katika mfumo wa MATLAB. Toleo huanza kwenye laini mpya, na data ya nambari ikiingizwa ndani na data ya maandishi ikiingizwa ndani. Ili kuhifadhi nafasi katika kitabu hiki, matokeo yajayo yatatolewa bila laini mpya. Kwa mfano, kutoa vekta ya safu
itatolewa kwa fomu:
Isipokuwa ni pato la vekta za safu na matrices - hapa fomu ya pato zaidi ya kuona na chaguo-msingi ya MATLAB itahifadhiwa.
Katika baadhi ya matukio, usemi wa hisabati unaoweka unaweza kuwa mrefu kiasi kwamba mstari mmoja hautoshi kwake. Kisha sehemu ya usemi inaweza kuhamishwa hadi kwenye mstari mpya kwa kutumia ellipsis "..." (doti 3 au zaidi), kwa mfano:
s = 1 - 1/2 + 1/3 - 1/4 + 1/5 - 1/6 + 1/7 ...
1/8 + 1/9 - 1/10 + 1/11 - 1/12;
Idadi ya juu ya wahusika katika mstari mmoja wa hali ya amri ni 4096, na katika faili ya m sio mdogo, lakini ni vigumu kufanya kazi na mistari hiyo ndefu. Katika matoleo ya awali, mstari mmoja ulikuwa na upeo wa herufi 256.
Kuendesha Mifano ya MATLAB kutoka kwa Mstari wa Amri
MATLAB ina mifano mingi ya maombi, ambayo baadhi inaweza kuendeshwa moja kwa moja kutoka kwa mstari wa amri. Kwa mfano, amri
huendesha m-file bench.m ya onyesho la majaribio ya mfumo.
1. Unaweza kuanza programu kwa kutumia icon kwenye desktop au kupitia kifungo cha Mwanzo (katika kona ya chini kushoto ya skrini). Mazingira ya kufanya kazi ya MatLab yatafunguliwa.

2. Bofya kwenye uwanja wa Dirisha la Amri ili kuifanya iwe hai.
Andika 1+2 kwenye mstari ukitumia aikoni ya " na kishale wima kinachometa na ubonyeze Enter. Kama matokeo, dirisha la amri ya MatLab linaonyesha yafuatayo:

Matokeo ya kuhesabu jumla ya 1 + 2 imeandikwa kwa ans maalum ya kutofautiana na thamani yake, sawa na 3, inaonyeshwa kwenye dirisha la amri. Chini ya jibu ni mstari wa amri na mshale unaowasha, unaoonyesha kuwa MatLab iko tayari kwa mahesabu zaidi. Unaweza kuandika maneno mapya kwenye mstari wa amri na kupata maana zao.
3. Ili kuendelea kufanya kazi na usemi uliopita, kwa mfano, kuhesabu (1 + 2) / 4.5, ni vyema kutumia matokeo yaliyopo, ambayo yanahifadhiwa katika kutofautiana kwa ans.
Andika ans/4.5 (kitone hutumika wakati wa kuingiza desimali) na ubonyeze Enter, utapata:

4.Ingizo "ans = 0.6667" inaitwa echo.
Utekelezaji wa kila amri katika MatLab unaambatana na mwangwi sawa, ambao mara nyingi hufanya iwe vigumu kutambua uendeshaji wa programu.
Ili kuzima echo, fuata amri na ishara; (semicolon). Kwa mfano:

Hapa matokeo ya kuzidisha ans kutofautiana na 3, ambayo ni ya kati, haijachapishwa kwenye skrini. Jibu la mwisho pekee ndilo limeonyeshwa.
5.Hifadhi maadili ya kutofautiana. Kwa hii; kwa hili:
— chagua Hifadhi Nafasi ya Kazi Kama kwenye menyu ya Faili;
- katika sanduku la mazungumzo la Hifadhi Vigezo vya Nafasi ya Kazi inayoonekana, taja saraka na jina la faili (kwa chaguo-msingi, inapendekezwa kuhifadhi faili kwenye safu ndogo ya kazi ya saraka kuu ya MatLab). Matokeo ya kazi yatahifadhiwa kwenye faili iliyo na mkeka wa ugani.
6. Funga MatLab.
7.Anzisha MatLab tena. Ili kurejesha maadili ya vigezo kutoka kwa kikao cha awali cha kazi, fungua faili iliyohifadhiwa kwa kutumia kitu kidogo cha Fungua kwenye menyu ya Faili. Vigezo vilivyohifadhiwa vinaweza kutumika katika amri mpya zilizoingizwa.
8.Andika amri zinazoweza kutekelezwa na matokeo kwenye faili ya maandishi, ambayo inaweza kusomwa au kuchapishwa kutoka kwa mhariri wa maandishi. Kwa hii; kwa hili:
- ingiza amri ya diary;
- taja jina la faili ambayo logi ya kazi itahifadhiwa kama hoja kwa amri ya diary.
Mfano umetolewa katika aya ya 1.3.
9. Ili kuondoka kwenye mfumo wa MatLab, ingiza amri ya kuacha.
1. Jifunze sehemu ya kinadharia.
2. Pata lahaja ya kazi.
3. Fuata mfano uliotolewa katika aya ya 2.
4. Fanya mahesabu kulingana na chaguo lako.
5. Peana ripoti kwa njia ya kielektroniki.
6. Tetea kazi yako ya maabara kwa kujibu maswali ya mwalimu.
Chaguo
Makala ya kusoma:
Misingi ya kufanya kazi na Mathcad. Mahesabu rahisi. Somo la 4
na masharti ya mipaka y(t 0 , t mwisho, uk) = y, Wapi t mwisho, t 0 ni sehemu za kuanzia na za mwisho za vipindi. Kigezo t(kutofautisha huru) haimaanishi wakati, ingawa mara nyingi suluhisho la DE hutafutwa katika kikoa cha saa. Mfumo wa DE katika fomu ya Cauchy umeandikwa sawa na (1.1), lakini chini ya y katika kesi hii, vector ya safu ya vigezo tegemezi ina maana. Vekta uk huweka masharti ya awali.
Ili kutatua DE za mpangilio wa pili na wa juu, zinahitaji kupunguzwa kwa utaratibu wa kwanza wa DE.
Kuna uwezekano wa milinganyo ya kutofautisha ambayo hairuhusiwi kuhusiana na derivative:
| F(t, y, dy/dt) = 0. | (1.2) |
Milinganyo (1.2) kwa kawaida haiwezi kupunguzwa kiuchanganuzi hadi kuunda (1.1). Walakini, suluhisho la nambari haisababishi ugumu wowote wa kuamua f(y, t) suluhisha (1.2) kwa nambari kwa heshima na derivati ya kutolewa y Na t.
Vitatuzi vya ODE
Mbinu mbalimbali za nambari zinatekelezwa katika MATLAB kutatua mifumo ya ODE. Utekelezaji wao umetajwa vitatuzi ODU.
Katika sehemu hii, kisuluhishi cha jina la jumla kinamaanisha mojawapo ya mbinu za nambari zinazowezekana za kutatua ODE: ode45, ode23, ode113, ode15s, ode23s, ode23t, ode23tb, bvp4c au pdepe.
Watatuzi hutumia njia zifuatazo za kutatua mifumo ya DE:
Ode45 ya hatua moja inafafanua mbinu za Runge-Kutta za agizo la 4 na la 5 zilizorekebishwa na Dormand na Prince. Hii ndio njia ya kawaida inayopendekezwa kwa kujaribu suluhisho hapo awali. Katika hali nyingi hutoa matokeo mazuri ikiwa mfumo wa equations unatatuliwa sio ngumu.
Ode23 ya hatua moja inafafanua mbinu za Runge-Kutta za agizo la 2 na la 4 kama ilivyorekebishwa na Bogacki na Champin. Kwa ugumu wa wastani wa mfumo wa ODE na mahitaji ya chini ya usahihi, njia hii inaweza kutoa faida kwa kasi ya suluhisho.
Njia ya Ode113 ya hatua nyingi ya Adams-Bashworth-Moulton ya darasa la kitabiri-kisahihishaji cha mpangilio tofauti. Hii ni njia inayobadilika ambayo inaweza kutoa suluhisho sahihi sana.
Ode15s ni mbinu ya kutofautisha ya hatua nyingi (kutoka 1 hadi 5, chaguo-msingi 5) kwa kutumia fomula za "utofautishaji wa nyuma" wa nambari. Hii ni njia ya kubadilika na inapaswa kutumiwa ikiwa kisuluhishi cha ode45 hakitoi suluhisho na mfumo wa udhibiti wa kijijini ni mgumu.
Ode23s ni mbinu ya hatua moja kwa kutumia fomula iliyorekebishwa ya agizo la 2 la Rosenbrock. Inaweza kutoa kasi ya juu ya hesabu na usahihi mdogo wa kutatua mfumo wa udhibiti wa kijijini.
Ode23t njia ya trapezoid isiyo wazi yenye ukalimani. Njia hii inatoa matokeo mazuri wakati wa kutatua matatizo ambayo yanaelezea mifumo ya oscillatory na ishara ya pato karibu ya harmonic. Kwa mifumo ngumu ya wastani, DE inaweza kutoa suluhisho sahihi sana.
Ode23tb mbinu ya Runge Kutta isiyo wazi mwanzoni mwa suluhisho na mbinu ya kutumia fomula za upambanuzi za kurudi nyuma za mpangilio wa 2 baadaye. Licha ya usahihi wa chini, njia hii inaweza kuwa na ufanisi zaidi kuliko ode15s.
Bvp4c hutumikia tatizo la thamani ya mipaka ya mifumo ya udhibiti wa kijijini ya fomu y′ = f(t, y), F(y(a), y(b), uk) = 0 (aina kamili ya mfumo wa milinganyo ya Cauchy). Matatizo yanayotatua huitwa matatizo ya thamani ya mipaka ya pointi mbili, kwa kuwa suluhisho hutafutwa kwa kubainisha masharti ya mipaka mwanzoni na mwisho wa muda wa ufumbuzi.
Vitatuzi vyote vinaweza kutatua mifumo ya milinganyo iliyo wazi y′ = F(t, y), na kutatua mifumo ngumu ya milinganyo inashauriwa kutumia visuluhishi maalum tu ode15s, ode23s, ode23t, ode23tb.
Kutumia Vitatuzi vya ODE
tspan vekta inayofafanua muda wa ujumuishaji [ t 0 t mwisho]. Ili kupata suluhisho kwa wakati maalum t 0 , t 1 , …, t mwisho(iliyopangwa kwa utaratibu wa kupungua au kuongezeka) lazima itumike tspan = [t 0 t 1 … t mwisho];
y 0 vector ya hali ya awali;
Hoja ya chaguzi zinazozalishwa na kitendakazi cha odeset (kitendakazi kingine cha odeget au bvpget (bvp4c pekee) hukuruhusu kuchapisha chaguo zilizowekwa na chaguo-msingi au kwa kazi ya odeset/bvpset);
uk 1, uk 2,... vigezo vya kiholela vilivyopitishwa kwenye kazi F;
T, Y matrix ya uamuzi Y, ambapo kila safu inalingana na wakati uliorejeshwa kwenye vekta ya safu wima T.
Wacha tuendelee kwenye maelezo ya syntax ya kazi za kutatua mifumo ya udhibiti wa kijijini (kitatuzi cha jina kinamaanisha kazi zozote zilizowasilishwa hapo juu).
[T,Y]=kisuluhishi(@ F,tspan,y 0) huunganisha mfumo wa udhibiti wa kijijini wa fomu y′ = F(t, y) kwa muda tspan na masharti ya awali y 0 . @F maelezo ya kazi ya ODE (unaweza pia kutaja kazi katika fomu " F") Kila safu katika safu ya suluhisho Y inalingana na thamani ya muda iliyorejeshwa katika vekta ya safu wima T.
[T,Y]=kisuluhishi(@ F,tspan,y 0 ,options) hutoa suluhisho sawa na ile iliyoelezwa hapo juu, lakini kwa chaguzi zilizoamuliwa na maadili ya hoja ya chaguzi iliyoundwa na kazi ya odeset. Vigezo vinavyotumika sana ni pamoja na uvumilivu wa hitilafu wa jamaa wa RelTol (chaguo-msingi 1e3) na vekta ya kustahimili makosa kabisa AbsTol (vijenzi vyote chaguo-msingi 1e6).
[T,Y]=kisuluhishi(@ F,tspan,y 0, chaguzi uk 1 ,uk 2...) hutoa suluhisho sawa na ile iliyoelezwa hapo juu, kupitisha vigezo vya ziada uk 1 , uk 2, ... katika m-faili F kila inapoitwa. Tumia chaguzi= ikiwa hakuna chaguzi zilizoainishwa.
Suluhisho la agizo la kwanza la ODE
UTARATIBU WA UTEKELEZAJI WA KAZI
· ukurasa wa kichwa;
· data ya awali ya chaguo;
· suluhisho la shida;
· matokeo ya kutatua tatizo.
Mfano
Pata suluhu la mlinganyo wa kutofautisha kwenye sehemu ambayo kwa ajili yake katika(1,7) = 5,3.
Unda kitendakazi cha mtumiaji kwenye Dirisha la Amri
g=@(x,y);
Katika syntax ya kazi @(x,y) x tofauti ya kujitegemea y tofauti tegemezi x-cos( y/pi) upande wa kulia wa kidhibiti cha mbali.
Mchakato wa suluhisho unafanywa kwa kupata kisuluhishi (suluhisho) kwenye Dirisha la Amri kwa kutumia opereta ifuatayo:
Ode23(g,,);
Ujenzi wa grafu yenye gridi ya taifa unafanywa na waendeshaji wafuatao:
Matokeo yanaonyeshwa kwenye Mtini. 1.1
Mchele. 1.2.1. Taswira ya suluhisho la nambari
MAZOEZI
1. Tafuta suluhu za milinganyo ya kutofautisha ya mpangilio wa kwanza  , kukidhi masharti ya awali y (x 0 ) = y 0 kwa muda [ a,b].
, kukidhi masharti ya awali y (x 0 ) = y 0 kwa muda [ a,b].
2. Jenga grafu za kazi.
Chaguzi za kazi.
| Chaguo Na. | 
| y (x 0 )=y 0 | [a,b] |
 | y 0 (1,8)=2,6 | ||
 | y 0 (0,6)=0,8 | ||
 | y 0 (2,1)=2,5 | ||
 | y 0 (0,5)=0,6 | ||
 | y 0 (1,4)=2,2 | ||
 | y 0 (1,7)=5,3 | ||
 | y 0 (1,4)=2,5 | ||
 | y 0 (1,6)=4,6 | ||
 | y 0 (1,8)=2,6 | ||
 | y 0 (1,7)=5,3 | ||
 | y 0 (0,4)=0,8 | ||
 | y 0 (1,2)=1,4 |
Kazi ya maabara nambari 2
Kutatua mifumo ya ODE
LENGO LA KAZI
Kuunda mawazo ya wanafunzi kuhusu matumizi ya mifumo ya udhibiti wa kijijini katika nyanja mbalimbali; kuingiza uwezo wa kutatua tatizo la Cauchy kwa mifumo ya udhibiti wa kijijini.
UTARATIBU WA UTEKELEZAJI WA KAZI
1. Jifunze sehemu ya kinadharia. Kamilisha kazi zinazolingana na nambari ya chaguo lako na uonyeshe kwa mwalimu.
2. Jaza ripoti ya maabara, ambayo inapaswa kuwa na:
· ukurasa wa kichwa;
· data ya awali ya chaguo;
· suluhisho la shida;
· matokeo ya kutatua tatizo.
Mfano
Tatua mfumo 
 kwa kutumia ode23() solver.
kwa kutumia ode23() solver.
Suluhisho:
1. Unda faili ya m ya chaguo za kukokotoa kwa ajili ya kukokotoa pande za kulia za kidhibiti cha mbali katika kihariri.
Acha jina katika kihariri faili liwe sisdu.m, basi kazi inaweza kuonekana kama hii:
kazi z=sisdu(t,y)
z1=-3*y(2)+cos(t)-exp(t);
z2=4*y(2)-cos(t)+2*exp(t);
>> t0=0;tf=5;y0=[-3/17,4/17];
>> =ode23("sisdu",,y0);
>>kiwanja(t,y)
Mchele. 1.3.1. Taswira ya suluhisho la nambari iliyopatikana kwa kutumia kazi ya ode23.
1. Inamaanisha nini kutatua tatizo la Cauchy kwa mfumo wa udhibiti wa kijijini?
2. Ni njia gani zilizopo za kutatua mifumo ya udhibiti wa kijijini?
MAZOEZI
1. Pata suluhisho kwa mfumo wa udhibiti wa kijijini

kukidhi masharti ya awali kwa muda;
2. Jenga grafu za kazi.
Kwa mfano, kazi ya suluhisho kwa chaguo la 8 imepewa:
kazi z=ssisdu(t,y)
% chaguo 8
z1=-a*y(1)+a*y(2);
z2=a*y(1)-(a-m)*y(2)+2*m*y(3);
z3=a*y(2)-(a-m)*y(3)+3*m*y(4);
z4=a*y(3)-3*m*y(4);
>> =ode23("ssisdu",,);
>> plot(t,100*y)
Mchele. 1.3.2. Taswira ya suluhisho la nambari iliyopatikana kwa kutumia kazi ya ode23.
Chaguzi za kazi.
| Chaguo Na. | Kazi | |
| a | m | |
| 0,1 | 1,2 | |
| 0,2 | 1,5 | |
| 0,3 | 1,7 | |
| 0,4 | 1,9 | |
| 0,5 | ||
| 0,6 | 1,9 | |
| 0,7 | 2,3 | |
| 0,8 | 2,7 | |
| 0,9 | ||
| 0,1 | 1,5 | |
| 0,2 | 1,1 | |
| 0,3 |
Kazi ya maabara nambari 3
1.4 Suluhisho la ODE n- utaratibu
LENGO LA KAZI
Kuunda maoni ya wanafunzi juu ya utumiaji wa udhibiti wa kijijini wa hali ya juu katika nyanja mbali mbali; ongeza uwezo wa kutatua shida ya Cauchy kwa milinganyo ya hali ya juu kwa kutumia programu za programu; kukuza ujuzi katika kuangalia matokeo yaliyopatikana.
UTARATIBU WA UTEKELEZAJI WA KAZI
1. Jifunze sehemu ya kinadharia. Kamilisha kazi zinazolingana na nambari ya chaguo lako na uonyeshe kwa mwalimu.
2. Jaza ripoti ya maabara, ambayo inapaswa kuwa na:
· ukurasa wa kichwa;
· data ya awali ya chaguo;
· suluhisho la shida;
· matokeo ya kutatua tatizo.
Mfano 1.
Tatua milinganyo tofauti ya mpangilio wa pili  kutokana na masharti ya awali
kutokana na masharti ya awali  .
.
Suluhisho:
Kwanza tunaleta udhibiti wa kijijini kwenye mfumo:

1. Unda faili ya m ya kazi kwa kuhesabu pande za kulia za udhibiti wa kijijini.
Acha jina la faili liwe sisdu_3.m, basi chaguo la kukokotoa linaweza kuonekana kama hii:
kazi z=sisdu_3(x,y)
z2=6*x*exp(x)+2*y(2)+y(1);
2. Fanya hatua zifuatazo:
>> x0=0;xf=10;y0=;
>> =ode23("sisdu_3",,y0);
>> plot(x,y(:,1))
Mchele. 1.4.1. Taswira ya suluhisho la nambari iliyopatikana kwa kutumia kazi ya ode23.
SAMPULI YA MASWALI YA KUTETEA KAZI
1. Inamaanisha nini kusuluhisha tatizo la Cauchy kwa milinganyo ya viwango vya juu zaidi?
2. Jinsi ya kuleta udhibiti wa kijijini m-th ili kwa mfumo wa udhibiti wa kijijini?
MAZOEZI
1. Tafuta suluhisho la mlinganyo wa kutofautisha ambao unakidhi masharti ya awali kwenye muda.
2. Jenga grafu za kazi.
Chaguzi za kazi.
| Chaguo Na. | Kazi | |
| Milinganyo | Masharti ya awali | |
 |  |
|
 |  |
|
 |  |
|
 |
||
 |
||
 |  |
|
 |
||
 |  |
|
 |  |
|
 |  |
|
 |  |
|
 |
Kazi ya maabara No 4 - 5
Mifumo ya Nguvu (DS)
LENGO LA KAZI
Kuanzisha wanafunzi kwa dhana za kimsingi za DS, uainishaji wao, nafasi ya awamu ya DS, tafsiri ya kinematic ya mfumo wa DS, mageuzi ya DS. Mlinganyo wa mwendo wa pendulum. Mienendo ya oscillator ya Van der Pol.
2. Mfumo wa Nguvu (DS) kitu cha hisabati kinacholingana na mifumo halisi (kimwili, kemikali, kibaiolojia, n.k.), mageuzi ambayo yamedhamiriwa kipekee na hali ya awali. DS huamuliwa na mfumo wa milinganyo (tofauti, tofauti, shirikishi, n.k.) ambayo inaruhusu kuwepo kwa suluhisho la kipekee kwa kila hali ya awali kwa muda usio na kipimo.
Hali ya DS inaelezewa na seti ya vigezo vilivyochaguliwa kwa sababu za asili ya tafsiri yao, unyenyekevu wa maelezo, ulinganifu, nk. Seti ya majimbo ya DS huunda nafasi ya awamu, kila hali inalingana na hatua ndani yake, na mageuzi yanaonyeshwa na trajectories (awamu). Kuamua ukaribu wa majimbo, dhana ya umbali huletwa katika nafasi ya awamu ya DS. Seti ya majimbo kwa wakati uliowekwa kwa wakati ina sifa ya kiasi cha awamu.
Maelezo ya DS kwa maana ya kubainisha sheria ya mageuzi pia inaruhusu aina kubwa: inafanywa kwa kutumia hesabu za kutofautisha, ramani za kipekee, kwa kutumia nadharia ya grafu, nadharia ya minyororo ya Markov, nk. Uchaguzi wa mojawapo ya mbinu za maelezo hubainisha aina maalum ya mfano wa hisabati wa DS inayofanana.
Mfano wa hisabati wa DS inazingatiwa ikitolewa ikiwa vigezo vya nguvu (viratibu) vya mfumo vinatambulishwa ambavyo huamua hali yake ya kipekee, na sheria ya mabadiliko ya serikali kwa muda imeonyeshwa.
Kulingana na kiwango cha makadirio, mifano tofauti ya hisabati inaweza kupewa mfumo huo. Utafiti wa mifumo halisi hufuata njia ya kusoma mifano inayolingana ya hesabu, uboreshaji na maendeleo ambayo imedhamiriwa na uchambuzi wa matokeo ya majaribio na kinadharia na kulinganisha kwao. Katika suala hili, kwa mfumo wa nguvu tutaelewa kwa usahihi mfano wake wa hisabati. Kwa kusoma mfumo sawa wa nguvu (kwa mfano, harakati ya pendulum), kulingana na kiwango ambacho mambo mbalimbali yanazingatiwa, tutapata mifano tofauti ya hisabati.