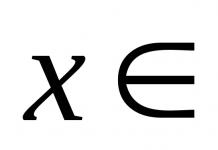Het nummer e wordt gebeld. Functie: domein van definitie en domein van waarden van functies. Uitdrukkingen die trigonometrische functies gebruiken

Voordat we het concept van een natuurlijke logaritme introduceren, bekijken we eerst het concept van een constant getal $e$.

Nummer $e$

Definitie 1

Nummer $e$ is een wiskundige constante die een transcendentaal getal is en gelijk is aan $e\ca. 2,718281828459045\ldots$.

Definitie 2

Transcendente is een getal dat niet de wortel is van een polynoom met gehele coëfficiënten.

Opmerking 1

De laatste formule beschrijft tweede prachtige limiet.

Het getal e wordt ook wel genoemd Euler-nummers, en soms Napier-nummers.

Opmerking 2

Om de eerste cijfers van het getal $е$ te onthouden wordt vaak de volgende uitdrukking gebruikt: "$2$, $7$, tweemaal Leo Tolstoj". Om het te kunnen gebruiken, is het natuurlijk noodzakelijk om te onthouden dat Leo Tolstoj werd geboren in $1828$. Het zijn deze getallen die twee keer worden herhaald in de waarde van het getal $e$ na het gehele getal $2$ en het decimale gedeelte $7$.

We begonnen het concept van het getal $e$ te overwegen bij het bestuderen van de natuurlijke logaritme, juist omdat het aan de basis ligt van de logaritme $\log_(e)⁡a$, die gewoonlijk wordt genoemd natuurlijk en schrijf het in de vorm $\ln ⁡a$.

Natuurlijke logaritme

Vaak worden bij berekeningen logaritmen gebruikt, waarvan de basis het getal $е$ is.

Definitie 4

Er wordt een logaritme met grondtal $e$ aangeroepen natuurlijk.

Die. de natuurlijke logaritme kan worden genoteerd als $\log_(e)⁡a$, maar in de wiskunde is het gebruikelijk om de notatie $\ln ⁡a$ te gebruiken.

Eigenschappen van de natuurlijke logaritme

Omdat de logaritme van een eenheidsgrondslag is gelijk aan $0$, dan is de natuurlijke logaritme van eenheid gelijk aan $0$:

De natuurlijke logaritme van het getal $е$ is gelijk aan één:

De natuurlijke logaritme van het product van twee getallen is gelijk aan de som van de natuurlijke logaritmes van deze getallen:

$\ln ⁡(ab)=\ln ⁡a+\ln ⁡b$.

De natuurlijke logaritme van het quotiënt van twee getallen is gelijk aan het verschil van de natuurlijke logaritmes van deze getallen:

$\ln⁡\frac(a)(b)=\ln ⁡a-\ln⁡ b$.

De natuurlijke logaritme van een macht van een getal kan worden weergegeven als het product van de exponent en de natuurlijke logaritme van het sublogaritmische getal:

$\ln⁡ a^s=s \cdot \ln⁡ a$.

Voorbeeld 1

Vereenvoudig de uitdrukking $\frac(2 \ln ⁡4e-\ln ⁡16)(\ln ⁡5e-\frac(1)(2) \ln ⁡25)$.

Oplossing.

Laten we de eigenschap van de productlogaritme toepassen op de eerste logaritme in de teller en de noemer, en de eigenschap van de machtslogaritme op de tweede logaritme van de teller en de noemer:

$\frac(2 \ln ⁡4e-\ln⁡16)(\ln ⁡5e-\frac(1)(2) \ln ⁡25)=\frac(2(\ln ⁡4+\ln ⁡e) -\ln⁡ 4^2)(\ln ⁡5+\ln ⁡e-\frac(1)(2) \ln⁡ 5^2)=$

Laten we de haakjes openen en vergelijkbare termen presenteren, en ook de eigenschap $\ln ⁡e=1$ toepassen:

$=\frac(2 \ln ⁡4+2-2 \ln ⁡4)(\ln ⁡5+1-\frac(1)(2) \cdot 2 \ln ⁡5)=\frac(2)( \ln ⁡5+1-\ln ⁡5)=2$.

Antwoord: $\frac(2 \ln ⁡4e-\ln ⁡16)(\ln ⁡5e-\frac(1)(2) \ln ⁡25)=2$.

Voorbeeld 2

Zoek de waarde van de uitdrukking $\ln⁡ 2e^2+\ln \frac(1)(2e)$.

Oplossing.

Laten we de formule voor de som van logaritmen toepassen:

$\ln 2e^2+\ln \frac(1)(2e)=\ln 2e^2 \cdot \frac(1)(2e)=\ln ⁡e=1$.

Antwoord: $\ln 2e^2+\ln \frac(1)(2e)=1$.

Voorbeeld 3

Bereken de waarde van de logaritmische uitdrukking $2 \lg ⁡0.1+3 \ln⁡ e^5$.

Oplossing.

Laten we de eigenschap van de logaritme van een macht toepassen:

$2 \lg ⁡0.1+3 \ln e^5=2 \lg 10^(-1)+3 \cdot 5 \ln ⁡e=-2 \lg ⁡10+15 \ln ⁡e=-2+ 15= $ 13.

Antwoord: $2 \lg ⁡0,1+3 \ln e^5=13$.

Voorbeeld 4

Vereenvoudig de logaritmische uitdrukking $\ln \frac(1)(8)-3 \ln ⁡4$.

$3 \ln \frac(9)(e^2)-2 \ln ⁡27=3 \ln (\frac(3)(e))^2-2 \ln 3^3=3 \cdot 2 \ln \ frac(3)(e)-2 \cdot 3 \ln ⁡3=6 \ln \frac(3)(e)-6 \ln ⁡3=$

Op de eerste logaritme passen we de eigenschap van de logaritme van het quotiënt toe:

$=6(\ln ⁡3-\ln ⁡e)-6 \ln⁡ 3=$

Laten we de haakjes openen en vergelijkbare termen presenteren:

$=6 \ln ⁡3-6 \ln ⁡e-6 \ln ⁡3=-6$.

Antwoord: $3 \ln \frac(9)(e^2)-2 \ln ⁡27=-6$.

2,7182818284590452353602874713527… Hexadecimaal 2,B7E151628AED2A6A… zestigtallig 2; 43 05 48 52 29 48 35 … Rationele benaderingen 8 / 3 ; 11 / 4 ; 19 / 7 ; 87 / 32 ; 106 / 39 ; 193 / 71 ; 1264 / 465 ; 2721 / 1001 ; 23225 / 8544

(vermeld in volgorde van toenemende nauwkeurigheid)

Vervolg fractie

Bepalingsmethoden

Nummer e kan op verschillende manieren worden gedefinieerd.

Over de limiet: e = lim X → ∞ (1 + 1 X) X (\displaystyle e=\lim _(x\to\infty )\left(1+(\frac (1)(x))\right)^(x) )(tweede opmerkelijke limiet). e = lim n → ∞ n n !}}} !} n (\ Displaystyle e = \ lim _ (n \ tot \ infty ) (\ frac (n) (\ sqrt [(n)] (n
(dit volgt uit de Moivre-Stirling-formule). Als de som van de reeks:}} !} e = ∑ n = 0 ∞ 1 n ! (\displaystyle e=\som _(n=0)^(\infty )(\frac (1)(n}} !}.
of 1 e = ∑ n = 2 ∞ (− 1) n n !(\displaystyle (\frac (1)(e))=\som _(n=2)^(\infty )(\frac ((-1)^(n))(n Als enkelvoud
een (\displaystyle a) 1 e = ∑ n = 2 ∞ (− 1) n n !, waarvoor ∫ 1 een d X X = 1. (\displaystyle \int \limits _(1)^(a)(\frac (dx)(x))=1.)

Als het enige positieve getal

, waarvoor het waar is
d d X een X = een X . (\displaystyle (\frac (d)(dx))a^(x)=a^(x).) Eigenschappen Bewijs van irrationaliteit Laten we dat aannemen e (\displaystyle e) rationeel. Dan e = p / q (\displaystyle e=p/q), Waar p (\ displaystyle p) - geheel, en Vermenigvuldig beide zijden van de vergelijking met (q − 1) ! !}(\displaystyle (q-1) , wij krijgen=\sum _{n=0}^{\infty }{q! \over n!}=\sum _{n=0}^{q}{q! \over n!}+\sum _{n=q+1}^{\infty }{q! \over n!}} !} p (q − 1) ! = gelijk!} !}= q! ∑ n = 0 ∞ 1 n !=p(q-1)!-\sum _{n=0}^{q}{q! \over n!}} !} = ∑ n = 0 ∞ q ! N! = ∑ n = 0 qq ! N! + (\displaystyle p(q-1)!=eq!=q!\sum _(n=0)^(\infty)(1 \over n< ∑ m = 1 ∞ 1 (q + 1) m {\displaystyle \sum _{n=q+1}^{\infty }{q! \over n!}=\sum _{m=1}^{\infty }{q! \over (q+m)!}=\sum _{m=1}^{\infty }{1 \over (q+1)...(q+m)}<\sum _{m=1}^{\infty }{1 \over (q+1)^{m}}} Wij transfereren ∑ n = 0 qq !< 1 q {\displaystyle \sum _{n=q+1}^{\infty }{q! \over n!}<{1 \over q}} N! (\displaystyle \som _(n=0)^(q)(q! \over n naar links:, ∑ n = 0 qq !< 1 {\displaystyle \sum _{n=q+1}^{\infty }{q! \over n!}<1} ∑ n = q + 1 ∞ q !

, waarvoor het waar is

d d X een X = een X . (\displaystyle (\frac (d)(dx))a^(x)=a^(x).) Eigenschappen Bewijs van irrationaliteit Laten we dat aannemen e (\displaystyle e) rationeel. Dan e = p / q (\displaystyle e=p/q), Waar

p (\ displaystyle p)

- geheel, en

Vermenigvuldig beide zijden van de vergelijking met (q − 1) ! !}(\displaystyle (q-1)

, wij krijgen=\sum _{n=0}^{\infty }{q! \over n!}=\sum _{n=0}^{q}{q! \over n!}+\sum _{n=q+1}^{\infty }{q! \over n!}} !}

p (q − 1) ! = gelijk!} !}= q!

∑ n = 0 ∞ 1 n !=p(q-1)!-\sum _{n=0}^{q}{q! \over n!}} !}

= ∑ n = 0 ∞ q !

N! = ∑ n = 0 qq !

N! + (\displaystyle p(q-1)!=eq!=q!\sum _(n=0)^(\infty)(1 \over n< ∑ m = 1 ∞ 1 (q + 1) m {\displaystyle \sum _{n=q+1}^{\infty }{q! \over n!}=\sum _{m=1}^{\infty }{q! \over (q+m)!}=\sum _{m=1}^{\infty }{1 \over (q+1)...(q+m)}<\sum _{m=1}^{\infty }{1 \over (q+1)^{m}}}

Wij transfereren

∑ n = 0 qq !< 1 q {\displaystyle \sum _{n=q+1}^{\infty }{q! \over n!}<{1 \over q}}

N! (\displaystyle \som _(n=0)^(q)(q! \over n naar links:,

∑ n = 0 qq !< 1 {\displaystyle \sum _{n=q+1}^{\infty }{q! \over n!}<1}

∑ n = q + 1 ∞ q !

Nummer (\displaystyle (\frac (d)(dx))a^(x)=a^(x).) N! = p (q − 1) ! (\displaystyle (\frac (d)(dx))a^(x)=a^(x).)− ∑ n = 0 qq !
N! (\displaystyle \som _(n=q+1)^(\infty )(q! \over n (\displaystyle (\frac (d)(dx))a^(x)=a^(x).) Alle termen aan de rechterkant zijn gehele getallen, daarom is de som aan de linkerkant een geheel getal. Maar deze som is ook positief, wat betekent dat deze niet minder dan 1 is.
Nummer e Aan de andere kant,
∑ n = q + 1 ∞ q ! N! = ∑ m = 1 ∞ q !
(q+m) ! (\displaystyle (\frac (d)(dx))a^(x)=a^(x).)= ∑ m = 1 ∞ 1 (q + 1) . .. (q + m)
Als we de geometrische progressie aan de rechterkant samenvatten, krijgen we: ∑ n = q + 1 ∞ q ! N! Sinds}z^{n}=\lim _{n\to \infty }\left(1+{\frac {z}{n}}\right)^{n}.} !}
Nummer e q ≥ 1 (\displaystyle q\geq 1) We krijgen een tegenspraak. transcendentaal. Dit werd voor het eerst bewezen in 1873 door Charles Hermite. Transcendentie van het getal e = 2 + 1 1 + 1 2 + 1 1 + 1 1 + 1 4 + 1 1 + 1 1 + 1 6 + 1 1 + 1 1 + 1 8 + 1 1 + 1 1 + 1 10 + 1 1 + … (\displaystyle e=2+(\cfrac (1)(1+(\cfrac (1)(2+(\cfrac (1)(1+(\cfrac (1)(1+(\cfrac (1)( ) 4+(\cfrac (1)(1+(\cfrac (1)(1+(\cfrac (1)(6+(\cfrac (1)(1+(\cfrac (1)(1+(\ cfrac (1)(8+(\cfrac (1)(1+(\cfrac (1)(1+(\cfrac (1)(10+(\cfrac (1)(1+\ldots ))))) )))))))))))))))))))))))))
Of gelijkwaardig daaraan: e = 2 + 1 1 + 1 2 + 2 3 + 3 4 + 4 … (\displaystyle e=2+(\cfrac (1)(1+(\cfrac (1)(2+(\cfrac (2)( ) 3+(\cfrac (3)(4+(\cfrac (4)(\ldots ))))))))))
Om snel een groot aantal tekens te berekenen, is het handiger om een andere uitbreiding te gebruiken: e + 1 e − 1 = 2 + 1 6 + 1 10 + 1 14 + 1 … (\displaystyle (\frac (e+1)(e-1))=2+(\cfrac (1)(6+( \cfrac (1)(10+(\cfrac (1)(14+(\cfrac (1)(\ldots )))))))))
e = lim n → ∞ n n !}}.} !}
N. (\ Displaystyle e = \ lim _ (n \ tot \ infty ) (\ frac (n) (\ sqrt [(n)] (n Vertegenwoordiging van het Catalaans:
e = 2 ⋅ 4 3 ⋅ 6 ⋅ 8 5 ⋅ 7 4 ⋅ 10 ⋅ 12 ⋅ 14 ⋅ 16 9 ⋅ 11 ⋅ 13 ⋅ 15 8 ⋅ 18 ⋅ 20 ⋅ 22 ⋅ 24 ⋅ 26 ⋅ 28 ⋅ 30 ⋅ 32 17 ⋅ 19 ⋅ 21 ⋅ 23 ⋅ 25 ⋅ 27 ⋅ 29 ⋅ 31 16 ⋯ (\displaystyle e=2\cdot (\sqrt (\frac (4)(3)))\cdot (\sqrt[(4)](\frac (6) \cdot 8)(5\cdot 7)))\cdot (\sqrt[(8)](\frac (10\cdot 12\cdot 14\cdot 16)(9\cdot 11\cdot 13\cdot 15)) )\cdot (\sqrt[(16)](\frac (18\cdot 20\cdot 22\cdot 24\cdot 26\cdot 28\cdot 30\cdot 32)(17\cdot 19\cdot 21\cdot 23\ cdot 25\cdot 27\cdot 29\cdot 31)))\cdots ) Vertegenwoordiging via het werk:
e = 3 ⋅ ∏ k = 1 ∞ (2 k + 3) k + 1 2 (2 k - 1) k - 1 2 (2 k + 1) 2 k (\displaystyle e=(\sqrt (3))\ cdot \prod \limits _(k=1)^(\infty )(\frac (\left(2k+3\right)^(k+(\frac (1)(2)))\left(2k-1\ rechts)^(k-(\frac (1)(2))))(\links(2k+1\rechts)^(2k))))

Via belnummers}} !}

E = 1 B n ∑ k = 0 ∞ k n k !

(\ Displaystyle e = (\ frac (1) (B_ (n))) \ som _ (k = 0) ^ (\ infty ) (\ frac (k ^ (n)) (k Verhaal Dit nummer wordt soms gebeld niet-gevederd ter ere van de Schotse wetenschapper Napier, auteur van het werk "Description of the Amazing Table of Logarithms" (1614). Deze naam is echter niet helemaal correct, omdat deze een logaritme van het getal heeft x (\displaystyle x).

De constante verschijnt voor het eerst stilzwijgend in een bijlage bij de Engelse vertaling van Napiers bovengenoemde werk, gepubliceerd in 1618. Achter de schermen, omdat het alleen een tabel bevat met natuurlijke logaritmen, bepaald op basis van kinematische overwegingen, maar de constante zelf is niet aanwezig.

De constante zelf werd voor het eerst berekend door de Zwitserse wiskundige Jacob Bernoulli toen hij het probleem van de beperkende waarde van rente-inkomsten oploste. Hij ontdekte dat als het oorspronkelijke bedrag $ 1 (\displaystyle \$1) en wordt jaarlijks eenmalig aan het eind van het jaar berekend, dan is het totaalbedrag $ 2 (\displaystyle \$2). Maar als dezelfde rente twee keer per jaar wordt berekend, dan wel $ 1 (\displaystyle \$1) vermenigvuldigd met 1, 5 (\displaystyle 1(,)5) tweemaal, krijgen $ 1, 00 ⋅ 1, 5 2 = $ 2, 25 (\displaystyle \$1(,)00\cdot 1(,)5^(2)=\$2(,)25). De driemaandelijkse renteopbouw resulteert in $ 1, 00 ⋅ 1, 25 4 = $ 2.441 40625 (\displaystyle \$1(,)00\cdot 1(,)25^(4)=\$2(,)44140625), enzovoort. Bernoulli toonde aan dat als de frequentie van renteberekeningen voor onbepaalde tijd wordt verhoogd, de rente-inkomsten in het geval van samengestelde rente een limiet hebben: lim n → ∞ (1 + 1 n) n .(\displaystyle \lim _(n\to\infty)\left(1+(\frac (1)(n))\right)^(n).) en deze limiet is gelijk aan het aantal.

e (≈ 2,718 28) (\ Displaystyle e ~ (\ ongeveer 2 (,) 71828))

$ 1, 00 ⋅ (1 + 1 12) 12 = $ 2.613.035... (\displaystyle \$1(,)00\cdot \left(1+(\frac (1)(12))\right)^( 12 )=\$2(,)613035...)

$ 1, 00 ⋅ (1 + 1.365) 365 = $ 2.714.568... (\displaystyle \$1(,)00\cdot \left(1+(\frac (1)(365))\right)^( 365) =\$2(,)714568...) (\displaystyle (\frac (d)(dx))a^(x)=a^(x).) De constante dus betekent de maximaal mogelijke jaarwinst op 100% (\displaystyle 100\%)

per jaar en maximale frequentie van rentekapitalisatie. Het eerste bekende gebruik van deze constante, waar deze werd aangegeven met de letter b (\ displaystyle b)

, gevonden in Leibniz' brieven aan Huygens, -1691. (\displaystyle (\frac (d)(dx))a^(x)=a^(x).) Brief (\displaystyle (\frac (d)(dx))a^(x)=a^(x).) Euler begon het te gebruiken in 1727. Het wordt voor het eerst aangetroffen in een brief van Euler aan de Duitse wiskundige Goldbach, gedateerd 25 november 1731, en de eerste publicatie met deze brief was zijn werk ‘Mechanics, or the Science of Motion, Analytisch uitgelegd’. 1736. Respectievelijk, meestal genoemd Euler-nummer . Hoewel sommige wetenschappers de brief vervolgens gebruikten c (\ Displaystyle c) (\displaystyle (\frac (d)(dx))a^(x)=a^(x).), brief

Het beschrijven van e als “een constante die ongeveer gelijk is aan 2,71828...” is hetzelfde als pi “een irrationeel getal noemen dat ongeveer gelijk is aan 3,1415...”. Dit is ongetwijfeld waar, maar het punt ontgaat ons nog steeds.

Pi is de verhouding van de omtrek tot de diameter, hetzelfde voor alle cirkels. Dit is de fundamentele verhouding die door alle cirkels wordt gedeeld en is daarom betrokken bij het berekenen van de omtrek, oppervlakte, volume en oppervlakte van cirkels, bollen, cilinders, enz. Pi laat zien dat alle cirkels gerelateerd zijn, om nog maar te zwijgen van de trigonometrische functies die zijn afgeleid van cirkels (sinus, cosinus, tangens).

Het getal e is de basisgroeiratio voor alle continu groeiende processen. Met het e-nummer kun je een eenvoudig groeipercentage nemen (waarbij het verschil pas aan het einde van het jaar zichtbaar is) en de componenten van deze indicator berekenen, normale groei, waarbij met elke nanoseconde (of zelfs sneller) alles een beetje groeit meer.

Het getal e is betrokken bij zowel exponentiële als constante groeisystemen: bevolking, radioactief verval, percentageberekening en vele, vele andere. Zelfs stapsystemen die niet gelijkmatig groeien, kunnen worden benaderd met behulp van het getal e.

Net zoals elk getal kan worden gezien als een "geschaalde" versie van 1 (de basiseenheid), kan elke cirkel worden gezien als een "geschaalde" versie van de eenheidscirkel (met straal 1). En elke groeifactor kan worden beschouwd als een "geschaalde" versie van e (de "eenheidsgroeifactor").

Het getal e is dus geen willekeurig getal. Het getal e belichaamt het idee dat alle voortdurend groeiende systemen geschaalde versies van dezelfde metriek zijn.

Concept van exponentiële groei

Laten we beginnen met te kijken naar het basissysteem verdubbelt voor een bepaalde periode. Bijvoorbeeld:

Bacteriën delen zich en “verdubbelen” elke 24 uur in aantal
We krijgen twee keer zoveel noedels als we ze doormidden breken
Je geld verdubbelt elk jaar als je 100% winst maakt (gelukkig!)

En het ziet er ongeveer zo uit:

Delen door twee of verdubbelen is een heel eenvoudige progressie. Natuurlijk kunnen we verdrievoudigen of verviervoudigen, maar verdubbelen is handiger voor uitleg.

Wiskundig gezien, als we x delingen hebben, eindigen we met 2^x keer meer goed dan waarmee we begonnen. Als er maar 1 partitie wordt gemaakt, krijgen we 2^1 keer meer. Als er 4 partities zijn, krijgen we 2^4=16 delen. De algemene formule ziet er als volgt uit:

hoogte= 2x

Met andere woorden: een verdubbeling is een stijging van 100%. We kunnen deze formule als volgt herschrijven:

hoogte= (1+100%) x

Dit is dezelfde gelijkheid, we hebben zojuist "2" in zijn samenstellende delen verdeeld, wat in wezen dit getal is: de beginwaarde (1) plus 100%. Slim, toch?

Natuurlijk kunnen we elk ander getal (50%, 25%, 200%) vervangen in plaats van 100% en zo de groeiformule voor deze nieuwe coëfficiënt verkrijgen. De algemene formule voor x perioden van de tijdreeks is:

hoogte = (1+toename)X

Dit betekent eenvoudigweg dat we het retourpercentage (1 + winst), "x" keer op rij gebruiken.

Laten we het eens nader bekijken

Onze formule gaat ervan uit dat groei in afzonderlijke stappen plaatsvindt. Onze bacteriën wachten en wachten en dan bam!, en op het laatste moment verdubbelen ze in aantal. Onze winst op de rente op de aanbetaling verschijnt op magische wijze over precies 1 jaar. Op basis van de hierboven geschreven formule groeit de winst in stappen. Er verschijnen plotseling groene stippen.

Maar de wereld is niet altijd zo. Als we inzoomen, kunnen we zien dat onze bacteriële vrienden zich voortdurend delen:

De groene kerel ontstaat niet uit het niets: hij groeit langzaam uit de blauwe ouder. Na 1 tijdsperiode (in ons geval 24 uur) is de groene vriend al volledig rijp. Als hij volwassen is geworden, wordt hij een volwaardig blauw lid van de kudde en kan hij zelf nieuwe groene cellen creëren.

Zal deze informatie onze vergelijking op enigerlei wijze veranderen?

Nee. In het geval van bacteriën kunnen de halfgevormde groene cellen nog steeds niets doen totdat ze opgroeien en volledig gescheiden zijn van hun blauwe ouders. De vergelijking klopt dus.

DEFINITIE

Nummer is een irrationele en transcendentale wiskundige constante genaamd meestal genoemd of Napier nummer, wat de basis is van de natuurlijke logaritme.

Achter de schermen constant is aanwezig in het werk "Description of the Amazing Table of Logarithms" van de Schotse wiskundige John Napier (1550-1617) (meer precies, in de bijlage bij de vertaling van dit werk, die in 1618 werd gepubliceerd). De eerste vermelding van deze constante is te vinden in de brieven van de Saksische filosoof, logicus, wiskundige, monteur, natuurkundige, jurist, historicus, diplomaat, uitvinder en taalkundige Gottfried Wilhelm Leibniz (1646-1716) aan de Nederlandse monteur, natuurkundige, wiskundige, astronoom en uitvinder Christian Huyngens van Zuilichem (1629-1695) in 1690-91. Daar werd het met de letter aangeduid. Traditionele aanduiding in 1727 begon de Zwitserse, Duitse, Russische wiskundige en monteur Leonhard Euler (1707-1783) het te gebruiken; hij gebruikte het voor het eerst in zijn brief aan de Duitse wiskundige Christian Goldbach (1690-1764) in 1731. De eerste publicatie met deze brief was het werk van L. Euler “Mechanics, or the Science of Motion, Explored Analytical” (1736). De constante zelf werd voor het eerst berekend door de Zwitserse wiskundige Jacob Bernoulli (1655-1705) terwijl hij het probleem van de grenswaarde van rente-inkomsten oploste:

Getal speelt een belangrijke rol in verschillende takken van de wiskunde, en vooral in de differentiaal- en integraalrekening. De transcendentie van het getal van Euler werd pas in 1873 bewezen door de Franse wiskundige Charles Hermite (1822-1901).

Aantal e-taken

1) Door de limiet:

Een functie is een model. Laten we X definiëren als een reeks waarden van een onafhankelijke variabele // onafhankelijk betekent elk.

Een functie is een regel waarmee voor elke waarde van de onafhankelijke variabele uit de verzameling X een unieke waarde van de afhankelijke variabele kan worden gevonden. // dat wil zeggen voor elke x is er één y.

Uit de definitie volgt dat er twee concepten zijn: een onafhankelijke variabele (die we aanduiden met x en deze kan elke waarde aannemen) en een afhankelijke variabele (die we aanduiden met y of f (x) en deze wordt berekend op basis van de functie wanneer wij vervangen x).

VOORBEELD y=5+x

1. Onafhankelijk is x, wat betekent dat we elke waarde aannemen, laat x=3

2. Laten we nu y berekenen, wat betekent y=5+x=5+3=8. (y hangt af van x, want welke x we ook vervangen, we krijgen y)

Er wordt gezegd dat de variabele y functioneel afhankelijk is van de variabele x en wordt als volgt aangegeven: y = f (x).

BIJVOORBEELD.

1.y=1/x. (zogenaamde hyperbool)

2. y=x^2. (parabool genoemd)

3.y=3x+7. (rechte lijn genoemd)

4. y= √x. (parabooltak genoemd)

De onafhankelijke variabele (die we aangeven met x) wordt het functieargument genoemd.