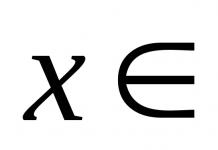Onder irrationeel een uitdrukking begrijpen waarin de onafhankelijke variabele %%x%% of de polynoom %%P_n(x)%% van graad %%n \in \mathbb(N)%% onder het teken staat radicaal(uit het Latijn radix- wortel), d.w.z. verheven tot een fractionele macht. Door een variabele te vervangen, kunnen sommige klassen van integranden die irrationeel zijn met betrekking tot %%x%% worden gereduceerd tot rationele uitdrukkingen met betrekking tot een nieuwe variabele.

Het concept van een rationale functie van één variabele kan worden uitgebreid tot meerdere argumenten. Als voor elk argument %%u, v, \dotsc, w%% bij het berekenen van de waarde van een functie alleen rekenkundige bewerkingen en het verheffen tot een gehele macht worden gegeven, dan spreken we van een rationale functie van deze argumenten, die meestal aangegeven als %%R(u, v, \ dotsc, w)%%. De argumenten van een dergelijke functie kunnen zelf functies zijn van de onafhankelijke variabele %%x%%, inclusief radicalen van de vorm %%\sqrt[n](x), n \in \mathbb(N)%%. Bijvoorbeeld de rationale functie $$ R(u,v,w) = \frac(u + v^2)(w) $$ met %%u = x, v = \sqrt(x)%% en %% w = \sqrt(x^2 + 1)%% is een rationale functie van $$ R\left(x, \sqrt(x), \sqrt(x^2+1)\right) = \frac(x + \sqrt(x ^2))(\sqrt(x^2 + 1)) = f(x) $$ van %%x%% en radicalen %%\sqrt(x)%% en %%\sqrt(x ^2 + 1 )%%, terwijl de functie %%f(x)%% een irrationele (algebraïsche) functie zal zijn van één onafhankelijke variabele %%x%%.

Laten we integralen bekijken van de vorm %%\int R(x, \sqrt[n](x)) \mathrm(d)x%%. Dergelijke integralen worden gerationaliseerd door de variabele %%t = \sqrt[n](x)%% te vervangen, en vervolgens %%x = t^n, \mathrm(d)x = nt^(n-1)%%.

Voorbeeld 1

Zoek %%\displaystyle\int \frac(\mathrm(d)x)(\sqrt(x) + \sqrt(x))%%.

De integrand van het gewenste argument wordt geschreven als een functie van radicalen van graad %%2%% en %%3%%. Omdat het kleinste gemene veelvoud van %%2%% en %%3%% %%6%% is, is deze integraal een integraal van het type %%\int R(x, \sqrt(x)) \mathrm(d) x %% en kan worden gerationaliseerd door %%\sqrt(x) = t%% te vervangen. Dan geldt %%x = t^6, \mathrm(d)x = 6t \mathrm(d)t, \sqrt(x) = t^3, \sqrt(x) =t^2%%. Daarom $$ \int \frac(\mathrm(d)x)(\sqrt(x) + \sqrt(x)) = \int \frac(6t^5 \mathrm(d)t)(t^3 + t^2) = 6\int\frac(t^3)(t+1)\mathrm(d)t. $$ Laten we nemen %%t + 1 = z, \mathrm(d)t = \mathrm(d)z, z = t + 1 = \sqrt(x) + 1%% en $$ \begin(array)( ll ) \int \frac(\mathrm(d)x)(\sqrt(x) + \sqrt(x)) &= 6\int\frac((z-1)^3)(z) \mathrm(d ) t = \\ &= 6\int z^2 dz -18 \int z \mathrm(d)z + 18\int \mathrm(d)z -6\int\frac(\mathrm(d)z)( z ) = \\ &= 2z^3 - 9 z^2 + 18z -6\ln|z| + C = \\ &= 2 \left(\sqrt(x) + 1\right)^3 - 9 \left(\sqrt(x) + 1\right)^2 + \\ &+~ 18 \left( \sqrt(x) + 1\right) - 6 \ln\left|\sqrt(x) + 1\right| + C \end(matrix) $$

Integralen van de vorm %%\int R(x, \sqrt[n](x)) \mathrm(d)x%% zijn een speciaal geval van fractionele lineaire irrationaliteiten, d.w.z. integralen van de vorm %%\displaystyle\int R\left(x, \sqrt[n](\dfrac(ax+b)(cd+d))\right) \mathrm(d)x%%, waarbij %% ad - bc \neq 0%%, wat kan worden gerationaliseerd door de variabele %%t = \sqrt[n](\dfrac(ax+b)(cd+d))%% te vervangen, en vervolgens %%x = \dfrac (dt^n - b)(a - ct^n)%%. Dan $$ \mathrm(d)x = \frac(n t^(n-1)(ad - bc))(\left(a - ct^n\right)^2)\mathrm(d)t. $$

Voorbeeld 2

Zoek %%\displaystyle\int \sqrt(\dfrac(1 -x)(1 + x))\dfrac(\mathrm(d)x)(x + 1)%%.

Laten we %%t = \sqrt(\dfrac(1 -x)(1 + x))%% nemen, en dan %%x = \dfrac(1 - t^2)(1 + t^2)%%, $ $ \begin(array)(l) \mathrm(d)x = -\frac(4t\mathrm(d)t)(\left(1 + t^2\right)^2), \\ 1 + x = \ frac(2)(1 + t^2), \\ \frac(1)(x + 1) = \frac(1 + t^2)(2). \end(array) $$ Daarom $$ \begin(array)(l) \int \sqrt(\dfrac(1 -x)(1 + x))\frac(\mathrm(d)x)(x + 1) = \\ = \frac(t(1 + t^2))(2)\left(-\frac(4t \mathrm(d)t)(\left(1 + t^2\right)^2 )\right) = \\ = -2\int \frac(t^2\mathrm(d)t)(1 + t^2) = \\ = -2\int \mathrm(d)t + 2\int \frac(\mathrm(d)t)(1 + t^2) = \\ = -2t + \text(arctg)~t + C = \\ = -2\sqrt(\dfrac(1 -x)( 1 + x)) + \text(arctg)~\sqrt(\dfrac(1 -x)(1 + x)) + C. \end(array) $$

Laten we integralen bekijken van de vorm %%\int R\left(x, \sqrt(ax^2 + bx + c)\right) \mathrm(d)x%%. In de eenvoudigste gevallen worden dergelijke integralen teruggebracht tot tabellarische integralen als, na het isoleren van het volledige vierkant, een verandering van variabelen wordt aangebracht.

Voorbeeld 3

Zoek de integraal %%\displaystyle\int \dfrac(\mathrm(d)x)(\sqrt(x^2 + 4x + 5))%%.

Gezien het feit dat %%x^2 + 4x + 5 = (x+2)^2 + 1%%, nemen we %%t = x + 2, \mathrm(d)x = \mathrm(d)t%%, dan $$ \begin(array)(ll) \int \frac(\mathrm(d)x)(\sqrt(x^2 + 4x + 5)) &= \int \frac(\mathrm(d)t) (\sqrt(t^2 + 1)) = \\ &= \ln\left|t + \sqrt(t^2 + 1)\right| + C = \\ &= \ln\left|x + 2 + \sqrt(x^2 + 4x + 5)\right| + C. \end(matrix) $$

In complexere gevallen wordt voor het vinden van integralen van de vorm %%\int R\left(x, \sqrt(ax^2 + bx + c)\right) \mathrm(d)x%% gebruikt

Definitie 1

De verzameling van alle primitieve functies van een gegeven functie $y=f(x)$, gedefinieerd op een bepaald segment, wordt de onbepaalde integraal van een gegeven functie $y=f(x)$ genoemd. De onbepaalde integraal wordt aangegeven met het symbool $\int f(x)dx $.

Opmerking

Definitie 2 kan als volgt worden geschreven:

\[\int f(x)dx =F(x)+C.\]

Niet elke irrationele functie kan via elementaire functies als een integraal worden uitgedrukt. De meeste van deze integralen kunnen echter worden gereduceerd door middel van vervangingen door integralen van rationale functies, die kunnen worden uitgedrukt in termen van elementaire functies.

$\int R\left(x,x^(m/n) ,...,x^(r/s) \right)dx $;

$\int R\left(x,\left(\frac(ax+b)(cx+d) \right)^(m/n) ,...,\left(\frac(ax+b)(cx +d) \right)^(r/s) \right)dx $;

$\int R\left(x,\sqrt(ax^(2) +bx+c) \right)dx $.

I

Bij het vinden van een integraal van de vorm $\int R\left(x,x^(m/n) ,...,x^(r/s) \right)dx $ is het noodzakelijk om de volgende substitutie uit te voeren:

Bij deze vervanging wordt elke fractionele macht van de variabele $x$ uitgedrukt via een gehele macht van de variabele $t$. Als gevolg hiervan wordt de integrandfunctie omgezet in een rationale functie van de variabele $t$.

Voorbeeld 1

Integratie uitvoeren:

\[\int \frac(x^(1/2) dx)(x^(3/4) +1) .\]

Oplossing:

$k=4$ is de gemeenschappelijke noemer van de breuken $\frac(1)(2) ,\, \, \frac(3)(4) $.

\ \[\begin(matrix)(l) (\int \frac(x^(1/2) dx)(x^(3/4) +1) =4\int \frac(t^(2) ) (t^(3) +1) \cdot t^(3) dt =4\int \frac(t^(5) )(t^(3) +1) dt =4\int \left(t^( 2) -\frac(t^(2) )(t^(3) +1) \right)dt =4\int t^(2) dt -4\int \frac(t^(2) )(t ^(3) +1) dt =\frac(4)(3) \cdot t^(3) -) \\ (-\frac(4)(3) \cdot \ln |t^(3) +1 |+C)\end(matrix)\]

\[\int \frac(x^(1/2) dx)(x^(3/4) +1) =\frac(4)(3) \cdot \left+C\]

II

Bij het vinden van een integraal van de vorm $\int R\left(x,\left(\frac(ax+b)(cx+d) \right)^(m/n) ,...,\left(\frac (ax+ b)(cx+d) \right)^(r/s) \right)dx $ Het is noodzakelijk om de volgende vervanging uit te voeren:

waarbij $k$ de gemeenschappelijke noemer is van de breuken $\frac(m)(n) ,...,\frac(r)(s) $.

Als resultaat van deze substitutie wordt de integrand getransformeerd in een rationale functie van de variabele $t$.

Voorbeeld 2

Integratie uitvoeren:

\[\int \frac(\sqrt(x+4) )(x) dx .\]

Oplossing:

Laten we de volgende vervanging maken:

\ \[\int \frac(\sqrt(x+4) )(x) dx =\int \frac(t^(2) )(t^(2) -4) dt =2\int \left(1 +\frac(4)(t^(2) -4) \right)dt =2\int dt +8\int \frac(dt)(t^(2) -4) =2t+2\ln \left |\frac(t-2)(t+2) \right|+C\]

Nadat we de omgekeerde vervanging hebben uitgevoerd, krijgen we het eindresultaat:

\[\int \frac(\sqrt(x+4) )(x) dx =2\sqrt(x+4) +2\ln \left|\frac(\sqrt(x+4) -2)(\ sqrt(x+4) +2) \right|+C.\]

III

Bij het vinden van een integraal van de vorm $\int R\left(x,\sqrt(ax^(2) +bx+c) \right)dx $ wordt de zogenaamde Euler-substitutie uitgevoerd (een van de drie mogelijke substituties is gebruikt).

Euler's eerste wissel

Voor het geval $a>

Als we het “+” teken voor $\sqrt(a) $ nemen, krijgen we

Voorbeeld 3

Integratie uitvoeren:

\[\int \frac(dx)(\sqrt(x^(2) +c) ) .\]

Oplossing:

Laten we de volgende vervanging uitvoeren (geval $a=1>0$):

\[\sqrt(x^(2) +c) =-x+t,\, \, x=\frac(t^(2) -c)(2t) ,\, \, dx=\frac(t ^(2) +c)(2t^(2) ) dt,\, \, \sqrt(x^(2) +c) =-\frac(t^(2) -c)(2t) +t= \frac(t^(2) +c)(2t) .\] \[\int \frac(dx)(\sqrt(x^(2) +c) ) =\int \frac(\frac(t^ (2) +c)(2t^(2) ) dt)(\frac(t^(2) +c)(2t) ) =\int \frac(dt)(t) =\ln |t|+C \]

Nadat we de omgekeerde vervanging hebben uitgevoerd, krijgen we het eindresultaat:

\[\int \frac(dx)(\sqrt(x^(2) +c) ) =\ln |\sqrt(x^(2) +c) +x|+C.\]

Euler's tweede wissel

Voor het geval $c>0$ is het noodzakelijk om de volgende vervanging uit te voeren:

Als we het “+” teken voor $\sqrt(c) $ nemen, krijgen we

Voorbeeld 4

Integratie uitvoeren:

\[\int \frac((1-\sqrt(1+x+x^(2) ))^(2) )(x^(2) \sqrt(1+x+x^(2) ) ) dx .\]

Oplossing:

Laten we de volgende vervanging maken:

\[\sqrt(1+x+x^(2) ) =xt+1.\]

\ \[\sqrt(1+x+x^(2) ) =xt+1=\frac(t^(2) -t+1)(1-t^(2) ) \] \

$\int \frac((1-\sqrt(1+x+x^(2) ))^(2) )(x^(2) \sqrt(1+x+x^(2) ) ) dx = \int \frac((-2t^(2) +t)^(2) (1-t)^(2) (1-t^(2))(2t^(2) -2t+2))( (1-t^(2))^(2) (2t-1)^(2) (t^(2) -t+1)(1-t^(2))^(2) ) dt =\ int \frac(t^(2) )(1-t^(2) ) dt =-2t+\ln \left|\frac(1+t)(1-t) \right|+C$ Nadat we het omgekeerde hebben gedaan vervanging, krijgen we het eindresultaat:

\[\begin(matrix)(l) (\int \frac((1-\sqrt(1+x+x^(2) ))^(2) )(x^(2) \sqrt(1+x +x^(2) ) dx =-2\cdot \frac(\sqrt(1+x+x^(2) ) -1)(x) +\ln \left|\frac(x+\sqrt(1 + x+x^(2) ) -1)(x-\sqrt(1+x+x^(2) ) +1) \right|+C=-2\cdot \frac(\sqrt(1+x + x^(2) ) -1)(x) +) \\ (+\ln \left|2x+2\sqrt(1+x+x^(2) ) +1\right|+C) \end ( matrix)\]

Euler's derde wissel

Een irrationele functie van een variabele is een functie die wordt gevormd uit een variabele en willekeurige constanten met behulp van een eindig aantal bewerkingen van optellen, aftrekken, vermenigvuldigen (verheffen tot een gehele macht), delen en worteltrekken. Een irrationele functie verschilt van een rationele functie doordat de irrationele functie bewerkingen bevat voor het extraheren van wortels.

Er zijn drie hoofdtypen irrationele functies, waarvan de onbepaalde integralen worden gereduceerd tot integralen van rationele functies. Dit zijn integralen die wortels bevatten van willekeurige gehele machten uit een lineaire fractionele functie (de wortels kunnen verschillende machten hebben, maar uit dezelfde lineaire fractionele functie); integralen van een differentiële binomiaal en integralen met de wortel van een vierkante trinominaal.

Belangrijke opmerking. Wortels hebben meerdere betekenissen!

Bij het berekenen van integralen die wortels bevatten, kom je vaak uitdrukkingen van de vorm tegen, waarbij een functie van de integratievariabele is. Dat moet in gedachten worden gehouden. Dat wil zeggen, op t >< 0, |t| = t. Bij t 0 0, |t| = - t.< 0 Daarom is het bij het berekenen van dergelijke integralen noodzakelijk om de gevallen t > afzonderlijk te beschouwen 0 en t< 0 .

Dit kan door het schrijven van borden of waar nodig. Aangenomen dat het bovenste teken verwijst naar het geval t >

, en de onderste - voor het geval t

.
,
Bij verdere transformatie heffen deze tekens elkaar in de regel op.
Er is ook een tweede benadering mogelijk, waarbij de integrand en het resultaat van integratie kunnen worden beschouwd als complexe functies van complexe variabelen. Dan hoef je niet op de tekens in radicale uitingen te letten. Deze benadering is toepasbaar als de integrand analytisch is, dat wil zeggen een differentieerbare functie van een complexe variabele. In dit geval zijn zowel de integrand als zijn integraal meerwaardige functies. Daarom is het na integratie, bij het vervangen van numerieke waarden, noodzakelijk om een ​​tak met één waarde (Riemann-oppervlak) van de integrand te selecteren, en daarvoor de overeenkomstige tak van het integratieresultaat te selecteren.
Fractionele lineaire irrationaliteit

Dit zijn integralen met wortels uit dezelfde fractionele lineaire functie: waarbij R een rationale functie is, zijn het rationale getallen, m 1, n 1, ..., m s, ns zijn gehele getallen, α, β, γ, δ zijn reële getallen.), of op de integratievariabele x (α = 1, β = 0, γ = 0, δ = 1).

Hier zijn voorbeelden van dergelijke integralen:
, .

Integralen uit differentiële binomialen

Integralen van differentiële binomialen hebben de vorm:
,
waarbij m, n, p rationale getallen zijn, a, b zijn reële getallen.
Dergelijke integralen worden in drie gevallen gereduceerd tot integralen van rationele functies.

1) Als p een geheel getal is. Vervanging x = t N, waarbij N de gemeenschappelijke noemer is van de breuken m en n.
2) Als - een geheel getal. Vervanging a x n + b = t M, waarbij M de noemer is van het getal p.
3) Als - een geheel getal. Vervanging a + b x - n = t M, waarbij M de noemer is van het getal p.

In andere gevallen worden dergelijke integralen niet uitgedrukt via elementaire functies.

Soms kunnen dergelijke integralen worden vereenvoudigd met behulp van reductieformules:
;
.

Integralen die de vierkantswortel van een vierkante trinominaal bevatten

Dergelijke integralen hebben de vorm:
,
waarbij R een rationale functie is. Voor elk van deze integraal zijn er verschillende methoden om deze op te lossen.
1) Het gebruik van transformaties leidt tot eenvoudigere integralen.
2) Pas trigonometrische of hyperbolische substituties toe.
3) Pas Euler-substituties toe.

Laten we deze methoden in meer detail bekijken.

1) Transformatie van de integrandfunctie

Door de formule toe te passen en algebraïsche transformaties uit te voeren, reduceren we de integrandfunctie tot de vorm:
,
waarbij φ(x), ω(x) rationale functies zijn.

Type ik

Integraal van de vorm:
,
waarbij Pn(x) een polynoom van graad n is.

Dergelijke integralen worden gevonden door de methode van onbepaalde coëfficiënten met behulp van de identiteit:

.
Door deze vergelijking te differentiëren en de linker- en rechterkant gelijk te stellen, vinden we de coëfficiënten A i.

Type II

Integraal van de vorm:
,
waarbij P m (x) een polynoom van graad m is.

Vervanging t = (x - α) -1 deze integraal wordt teruggebracht tot het vorige type. Als m ≥ n, dan moet de breuk een geheel getal hebben.

III-type

Hier doen we de vervanging:
.
Daarna zal de integraal de vorm aannemen:
.
Vervolgens moeten de constanten α, β zo worden gekozen dat de coëfficiënten van t in de noemer nul worden:
B=0, B1=0.
Vervolgens valt de integraal uiteen in de som van integralen van twee typen:
,
,
die zijn geïntegreerd door vervangingen:
u 2 = EEN 1 t 2 + C 1,
v 2 = EEN 1 + C 1 t -2 .

2) Trigonometrische en hyperbolische substituties

Voor integralen van de vorm a > 0 ,
we hebben drie belangrijke vervangingen:
;
;
;

Voor integralen geldt a > 0 ,
we hebben de volgende vervangingen:
;
;
;

En tenslotte, voor de integralen, a > 0 ,
de vervangingen zijn als volgt:
;
;
;

3) Euler-vervangingen

Ook kunnen integralen worden teruggebracht tot integralen van rationale functies van een van de drie Euler-substituties:
, voor a > 0;
, voor c > 0 ;
, waarbij x 1 de wortel is van de vergelijking a x 2 + b x + c = 0.

Elliptische integralen

Concluderend, overweeg integralen van de vorm:
,
waarbij R een rationale functie is, .

Dergelijke integralen worden elliptisch genoemd. Over het algemeen worden ze niet uitgedrukt via elementaire functies. Er zijn echter gevallen waarin er relaties bestaan ​​tussen de coëfficiënten A, B, C, D, E, waarin dergelijke integralen worden uitgedrukt door middel van elementaire functies.
.

Hieronder ziet u een voorbeeld met betrekking tot reflexieve polynomen. De berekening van dergelijke integralen wordt uitgevoerd met behulp van vervangingen:

Voorbeeld
.

Bereken de integraal:

Oplossing

.
Laten we een vervanging maken. 0 Hier bij x > 0 (u>< 0 ) neem het bovenste teken ′+ ′. Bij x< 0 (u

.

) - lagere ′- ′.

Antwoord
Gebruikte literatuur:

NM Günter, R.O. Kuzmin, Verzameling van problemen in de hogere wiskunde, “Lan”, 2003.

Kant-en-klare antwoorden over het integreren van functies komen uit de toets voor 1e en 2e jaars wiskunde-afdelingen. Om ervoor te zorgen dat de formules in de opgaven en antwoorden de voorwaarden van de taken niet herhalen, zullen we de voorwaarden niet uitschrijven. Je weet al dat je bij opgaven ‘de integraal moet zoeken’ of ‘de integraal moet berekenen’. Als u dus antwoorden nodig heeft over integratie, begin dan met het bestuderen van de volgende voorbeelden.

Integratie van irrationele functies

Voorbeeld 18. We voeren een verandering van variabelen uit onder de integraal. Om de berekeningen te vereenvoudigen, selecteren we niet alleen de wortel, maar de gehele noemer voor de nieuwe variabele. Na een dergelijke vervanging wordt de integraal getransformeerd naar de som van twee tabellarische integralen, die niet vereenvoudigd hoeven te worden
Na integratie vervangen we de variabele door een vervanging.

Voorbeeld 19. Er is veel tijd en ruimte besteed aan het integreren van deze fractionele irrationele functie en we weten niet eens of je dit kunt achterhalen vanaf een tablet of telefoon. Om van de irrationaliteit af te komen, en hier hebben we te maken met de derdemachtswortel, kiezen we voor de nieuwe variabele de wortelfunctie tot de derde macht. Vervolgens vinden we het differentieel en vervangen we de vorige functie door de integraal

Het meest tijdrovende onderdeel is het plannen van een nieuwe functie voor machtsverhoudingen en breuken.

Na de transformaties vinden we onmiddellijk enkele integralen, en schrijven we de laatste in twee, die we transformeren volgens de tabellarische integratieformules

Vergeet na alle berekeningen niet terug te keren naar de vervanging die aan het begin werd uitgevoerd

Voorbeeld 20. We moeten de integraal van sinus tot de 7e macht vinden. Volgens de regels moet één sinus in een differentiaal worden gedreven (we krijgen het differentieel van de cosinus), en de sinus tot de zesde macht moet door de cosinus worden geschreven. We komen dus tot integratie vanuit de functie van de nieuwe variabele t = cos (x).



In dit geval moet je het verschil naar de kubus brengen en vervolgens integreren
Als resultaat verkrijgen we een polynoom van orde 7 in cosinus.


Voorbeeld 21. In deze integraal is het noodzakelijk om de cosinus van de 4e graad in trigonometrische formules te schrijven door de afhankelijkheid van de cosinus van de eerste graad. Vervolgens passen we de tabelformule voor cosinusintegratie toe.

Voorbeeld 22. Onder de integraal hebben we het product van sinus en cosinus. Volgens trigonometrische formules schrijven we het product door het verschil in sinussen. Hoe deze boog werd verkregen, kan worden begrepen uit de analyse van de coëfficiënten voor “x”. Vervolgens integreren we de sinussen

Voorbeeld 23. Hier hebben we zowel een sinus- als een cosinusfunctie in de noemer. Bovendien zullen goniometrische formules de afhankelijkheid niet helpen vereenvoudigen. Om de integraal te vinden, passen we de universele trigonometrische vervanging t=tan(x/2) toe

Uit het verslag blijkt duidelijk dat de noemers elkaar opheffen en dat we een vierkante trinominaal krijgen in de noemer van de breuk. Daarin selecteren we een compleet vierkant en een vrij deel. Na integratie komen we uit op de logaritme van het verschil tussen de priemfactoren van de noemer. Om de notatie te vereenvoudigen, werden zowel de teller als de noemer onder de logaritme met twee vermenigvuldigd.
Aan het einde van de berekeningen vervangen we in plaats van de variabele de tangens van de helft van het argument.

Voorbeeld 24. Om de functie te integreren, nemen we het kwadraat van de cosinus tussen haakjes, en tussen haakjes trekken we er één af en tellen we er één op om de cotangens te krijgen.

Vervolgens kiezen we de cotangens u = ctg (x) voor de nieuwe variabele. Het differentieel ervan geeft ons de factor die we nodig hebben voor vereenvoudiging. Na substitutie komen we tot een functie die, wanneer geïntegreerd, de boogtangens oplevert.
Vergeet niet om u in cotangens te veranderen.


Voorbeeld 25. In de laatste taak van de test moet je de cotangens van een dubbele hoek tot de 4e graad integreren.
Op dit punt is de integratietest opgelost, en geen enkele leraar zal fouten vinden in de antwoorden en de rechtvaardiging voor de transformaties.

Als je op deze manier leert integreren, zijn tests of secties over het onderwerp integralen niet eng voor je. Alle anderen hebben de mogelijkheid om oplossingen van integralen bij ons (of onze concurrenten :))) te leren of te bestellen.

We blijven integralen van breuken en wortels beschouwen. Ze zijn niet allemaal supercomplex, alleen waren de voorbeelden om de een of andere reden een beetje ‘off-topic’ in andere artikelen.

Voorbeeld 9

In de noemer onder de wortel bevindt zich een kwadratische trinominale plus een "aanhangsel" in de vorm van een "X" buiten de wortel. Een dergelijke integraal kan worden opgelost met behulp van een standaardsubstitutie.

.

De vervanging is hier eenvoudig:

Laten we eens kijken naar het leven na vervanging:

(1) Na substitutie herleiden we de termen onder de wortel tot een gemeenschappelijke noemer.

(2) We halen het onder de wortel vandaan.

(3) De teller en de noemer worden verminderd met . Tegelijkertijd hebben we de termen in een handige volgorde onder de hoofdmap herschikt. Met enige ervaring kunnen stappen (1), (2) worden overgeslagen door de becommentarieerde acties mondeling uit te voeren.

(4) De resulterende integraal is, zoals u zich herinnert, opgelost volledige vierkante extractiemethode. Selecteer een compleet vierkant.

(5) Door integratie verkrijgen we een gewone “lange” logaritme.

(6) Wij voeren de omgekeerde vervanging uit. Indien aanvankelijk , dan terug: .

(7) De laatste actie is gericht op het rechttrekken van het resultaat: onder de wortel brengen we de termen opnieuw naar een gemeenschappelijke noemer en halen ze onder de wortel vandaan.

Voorbeeld 10

Voorbeeld 9

.

Dit is een voorbeeld dat u zelf kunt oplossen. Hier wordt een constante toegevoegd aan de enige “X”, en de vervanging is vrijwel hetzelfde:

.

Het enige dat nodig is, is om bovendien de “x” uit te drukken van de vervanging die wordt uitgevoerd:

.

Volledige oplossing en antwoord aan het einde van de les.

Soms kan er in zo'n integraal een kwadratische binomiaal onder de wortel staan, dit verandert niets aan de oplossingsmethode, het zal zelfs eenvoudiger zijn. Voel het verschil:

Voorbeeld 11

Voorbeeld 9

Voorbeeld 12

Voorbeeld 9

Korte oplossingen en antwoorden aan het einde van de les. Opgemerkt moet worden dat voorbeeld 11 precies is binominale integraal, waarvan de oplossing in de klas werd besproken Integralen van irrationele functies.

Integraal van een polynoom van de 2e graad, ontleedbaar in de noemer van de macht

Een zeldzamer type integraal, maar toch aangetroffen in praktische voorbeelden.

Voorbeeld 13

Voorbeeld 9

De noemer van de integrand bevat een kwadratische binominale waarde die niet in factoren kan worden ontbonden. We benadrukken dat niet-factoriseerbaarheid een essentieel kenmerk is. Als de polynoom wordt ontbonden, is alles veel duidelijker, bijvoorbeeld:

Laten we terugkeren naar het voorbeeld met geluksgetal 13. Deze integraal is er ook een die behoorlijk pijnlijk kan zijn als je niet weet hoe je deze moet oplossen.

De oplossing begint met een kunstmatige transformatie:

Ik denk dat iedereen al begrijpt hoe je de teller term voor term door de noemer deelt.

De resulterende integraal wordt in delen genomen:

Voor een integraal van de vorm

Waar ( k≥ 2) – natuurlijk getal, afgeleid terugkerend reductieformule:

; is een integraal van een graad lager dan 1.

Wat als er een extra polynoom in de teller staat? In dit geval wordt de methode van onbepaalde coëfficiënten gebruikt en wordt de integrand uitgebreid tot een som van breuken. Als je zo'n integraal tegenkomt, kijk dan naar het leerboek - daar is alles eenvoudig.