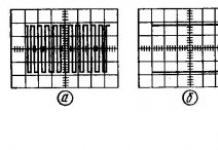
Fourier dan Hartley menukarkan fungsi masa kepada fungsi frekuensi yang mengandungi maklumat amplitud dan fasa. Di bawah ialah graf bagi fungsi selanjar g(t) dan diskret g(τ), di mana t dan τ detik masa.

Kedua-dua fungsi bermula pada sifar, melompat ke nilai positif, dan mereput secara eksponen. Mengikut takrifan, penjelmaan Fourier untuk fungsi berterusan adalah integral pada keseluruhan paksi nyata, F(f), dan untuk fungsi diskret jumlah ke atas set sampel terhingga, F(ν):

di mana f, nilai kekerapan ν, n bilangan nilai sampel fungsi, dan i=√ 1 unit khayalan. Perwakilan kamiran lebih sesuai untuk penyelidikan teori, dan perwakilan dalam bentuk jumlah terhingga lebih sesuai untuk pengiraan pada komputer. Transformasi Hartley integral dan diskret ditakrifkan dengan cara yang sama:

Walaupun satu-satunya perbezaan dalam tatatanda antara definisi Fourier dan Hartley ialah kehadiran faktor sebelum sinus, hakikat bahawa transformasi Fourier mempunyai kedua-dua bahagian nyata dan khayalan menjadikan perwakilan kedua-dua transformasi itu berbeza sama sekali. Transformasi Diskret Fourier dan Hartley pada dasarnya mempunyai bentuk yang sama dengan rakan sejawatannya.

Walaupun graf kelihatan berbeza, amplitud dan maklumat fasa yang sama boleh diperoleh daripada transformasi Fourier dan Hartley, seperti ditunjukkan di bawah.

Amplitud Fourier ditentukan oleh punca kuasa dua hasil tambah kuasa dua bahagian nyata dan khayalan. Amplitud Hartley ditentukan oleh punca kuasa dua hasil tambah kuasa dua H(ν) dan H(ν). Fasa Fourier ditentukan oleh arkatangen bahagian khayalan dibahagikan dengan bahagian nyata, dan fasa Hartley ditentukan oleh hasil tambah 45° dan arkatangen bagi H(ν) dibahagikan dengan H(ν).

Kami akan mulakan dengan gambar rajah mudah untuk merangkumi konsep asas yang akan kami gunakan kemudian untuk gambar rajah yang lebih kompleks. Dalam Rajah. 7.1 menunjukkan voltan masukan V BX.p = 1 V ialah gelombang sinus dengan frekuensi f=1 kHz dan nilai maksimum 1 V (nilai rms Vin=√2). Untuk menyediakan voltan keluaran yang merupakan fungsi tak linear bagi voltan masukan, sumber voltan terkawal voltan E (VCS) digunakan sebagai penguat. Dalam contoh ini, pergantungan voltan keluaran pada voltan masukan dipaparkan oleh fungsi

f(x) = 1 + X + X².

nasi. 7.1. Litar dengan sambungan tak linear antara voltan input dan output

Hubungan fungsian ini dipaparkan dalam perintah E menggunakan pekali polinomial. Pandangan umum polinomial:

f(X) = k 0 + k 1 X + k 2 X².

Untuk mendapatkan kebergantungan contoh kami, kami menggunakan tiga nombor terakhir arahan input E. Kami ingin melakukan analisis harmonik untuk melihat harmonik mana yang terdapat dalam voltan keluaran, tetapi mula-mula mari cuba tentukan apa yang sepatutnya kami jangkakan.

Sebelum meneruskan pengembangan kebergantungan masa siri Fourier, adalah perlu untuk melakukan analisis untuk proses sementara (program analisis sementara dalam PSpice).

Oleh itu, adalah perlu untuk menggunakan kedua-dua arahan .TRAN dan .FOUR. Biasanya, analisis sementara dilakukan untuk tempoh penuh frekuensi asas. Dalam contoh ini f=1 kHz; oleh itu, T=1/f=1 ms. Analisis harmonik mencerminkan komponen frekuensi sehingga harmonik kesembilan. Untuk kebanyakan tujuan ini sepatutnya lebih daripada mencukupi. Jika harmonik yang lebih tinggi ditunjukkan, ia tidak akan mempunyai banyak kepentingan kerana pengumpulan ralat pembundaran dalam keputusan.

Untuk memberikan penerangan yang lebih terperinci tentang voltan masukan V BX, gunakan borang dosa untuk menerangkan sumber. Parameter dosa( A, b,Dengan,...) bermaksud: A- komponen malar, b- nilai maksimum, Dengan- kekerapan, d- kelewatan, e- pekali pengecilan dan f- fasa.

Apabila arahan .FOUR dimasukkan ke dalam fail input, analisis harmonik dilakukan, memberikan pengembangan siri Fourier hasil analisis sementara. Parameter untuk arahan ini termasuk kekerapan asas dan pembolehubah yang mana penguraian akan diperolehi. Dalam contoh ini, pembolehubah tersebut akan menjadi fungsi berkala bagi voltan input V(1) dan output V(2). Fail input:

Vin 1 0 sin(0 1 1000); hujah untuk offset, maksimum dan kekerapan

E 2 0 poli(1) 1.0 1 1 1; 3 nilai terakhir untuk k0, k1, k2

Lakukan analisis, kemudian dapatkan graf V(1) dan (V)2. Pastikan V(1) ialah salinan tepat voltan masukan V VH. Voltan keluaran harus menunjukkan komponen DC dan gelombang kompleks dengan maksimum 3 V. Daripada kajian teori siri Fourier, seseorang boleh membuat kesimpulan bahawa graf ini menyerupai gelombang berkala yang terdiri daripada harmonik asas dan kedua. Adalah dinasihatkan untuk mencetak salinan graf ini untuk rujukan masa hadapan. Dalam Rajah. Rajah 7.2 menunjukkan graf ini.

nasi. 7.2. Graf voltan v 1 dan v 2 untuk litar dalam Rajah. 7.1

Pertimbangkan juga fail output untuk litar ini (Rajah 7.3), yang menunjukkan nilai berikut untuk voltan nod: V(1) = 0 V dan V(2) = 1 V. Ini bermakna walaupun isyarat input tidak mempunyai offset, output voltan mempunyai offset V(2)=1 V.

Dalam Rajah. 7.3 dalam jadual komponen siri Fourier untuk V(1), tidak semua komponen mempunyai nilai sebenar. Oleh itu, nilai komponen pemalar secara teorinya harus sama dengan sifar, tetapi analisis memberikan nilai yang sangat kecil iaitu 3.5E-10, yang tidak betul-betul sama dengan sifar disebabkan pengumpulan ralat pembundaran.

Analisis Fourier; Penguraian Polinomial

Vin 1 0 sin(0 1 1000); hujah diimbangi, puncak dan kekerapan

E 2 0 poli(1) 1.0 1 1 1; 3 1s terakhir adalah untuk k0, k1, k2

2 2.000E+03 1.994E-08 1.994E-08 -9.308E+01 -9.308E+01

5 5.000E+03 3.134E-09 3.134E-09 -9.107E+01 -9.107E+01

6 6.000E+03 1.525E-09 1.525E-09 -6.706E+01 -6.706E+01

KEKERAPAN HARMONIK EMPAT FASA BIASA DIBIASAKAN

NO (HZ) KOMPONEN KOMPONEN (DEG) FASA (DEG)

1 1.000E+03 1.000E+00 1.000E+00 -2.888E-07 0.000E+00

2 2.000E+03 5.000E-01 5.000E-01 -9.000E+01 -9.000E+01

3 3.000E+03 7.971E-08 7.971E-08 -1.546E+02 -1.546E+02

4 4.000E+03 5.126E-08 5.126E-08 -1.439E+02 -1.439E+02

5 5.000E+03 3.918E-08 3.918E-08 -1.420E+02 -1.420E+02

6 6.000E+03 3.327E-08 3.327E-08 -1.299E+02 -1.299E+02

7 7.000E+03 3.606E-08 3.606E-08 -1.268E+02 -1.268E+02

8 8.000E+03 2.889E-08 2.859E-08 -1.316E+02 -1.316E+02

9 9.000E+03 2.584E-08 2.584E-08 -1.189E+02 -1.189E+02

JUMLAH HEROTAN HARMONIK = 4.999939E+01 PERATUS

nasi. 7.3. Fail keluaran dengan keputusan analisis litar dalam Rajah. 7.1

Harmonik pertama ialah harmonik asas di f=1 kHz. Amplitud harmonik pertama siri Fourier dan fasanya ditunjukkan sebagai 2.4E-7 (juga hampir sifar). Jika kita menganggap bahawa komponen ini dinyatakan oleh formula

b n dosa( nx),

maka ini bermakna bahawa b 1 =1, n=1, di mana indeks 1 sepadan dengan kekerapan asas. Harmonik lain boleh diabaikan kerana amplitudnya banyak tertib magnitud lebih kecil daripada harmonik asas. Ia adalah harmonik asas yang dicerminkan dalam graf V(1) dalam Probe; ia diperoleh daripada data dalam Rajah. 7.3.

Satu lagi jadual komponen Fourier dalam Rajah. 7.3 terpakai kepada V(2). Apabila melihat pelbagai harmonik, perhatikan bahawa terdapat komponen DC 1.5 V. Mengapa 1.5 V? Komponen k 0 =1 V hanya memberikan sebahagian daripada nilai ini, baki 0.5 V dikaitkan dengan harmonik kedua. Teori ini menunjukkan bahawa dengan herotan harmonik pada harmonik kedua dalam voltan keluaran, sebagai tambahan kepada harmonik kedua itu sendiri dengan amplitud b 2, komponen malar yang dikaitkan dengan herotan pada harmonik kedua muncul dengan nilai b 0 =b 2. Amplitud frekuensi asas dalam pengembangan adalah sama dengan b 1 =1 V, amplitud harmonik kedua b 2 =0.5 V, sudut fasanya ialah -90°. Harmonik yang lebih tinggi adalah jauh lebih kecil dalam magnitud dan boleh diabaikan.

Sebagai latihan dalam sintesis harmonik, anda boleh memplot harmonik individu dan menambahnya untuk meramalkan keputusan yang akan anda perolehi dalam Probe untuk V(2). Ingat untuk mengambil kira komponen DC dan amplitud dan fasa yang sepadan untuk harmonik asas dan kedua. Sebaik sahaja anda telah melukis hayunan yang terhasil, anda pasti akan gembira mengetahui bahawa PSpice boleh melakukan kerja yang membosankan untuk anda.

Penambahan harmonik dan penguraian kepada komponen harmonik

Mari buat fail input baharu yang sepadan dengan Rajah. 7.4, di mana kepada rajah dalam Rajah. 7.1 dua lagi sumber semasa bebas telah ditambah.

Kami menggunakan dua sumber sahaja supaya anda boleh mendapatkan harmonik asas dan kedua pada graf yang sama dengan voltan keluaran. Sumber tambahan kuasa perintang 1-ohm disambung secara selari. Perubahan sedemikian kepada skema asal tidak sama sekali diperlukan, ia ternyata mudah untuk set parameter tertentu. Fail input baharu ialah lanjutan daripada fail sebelumnya dan kelihatan seperti ini:

Analisis Fourier; Penguraian Polinomial

Vin 1 0 sin(0 1 1000); hujah - offset, amplitud dan kekerapan

E 2 0 poli(1) 1.0 1 1 1; 3 penyertaan terakhir untuk k0, k1, k2

i2 0 3 sin(0.5 0.5 2000 0 0 -90)

nasi. 7.4. Litar untuk menganalisis penambahan harmonik dan pengembangan siri Fourier

Sebelum melakukan analisis, kami akan mempertimbangkan secara terperinci huraian untuk i 1 dan i 2. Untuk sintesis harmonik, hasil pengembangan siri Fourier daripada masalah sebelumnya digunakan. Pastikan anda memahami maksud semua parameter; kemudian jalankan analisis dalam Probe, menghasilkan plot I(i1), I(i2), dan I(r). Walaupun ia mewakili arus, ia secara berangka sama dengan voltan, kerana ia melalui rintangan 1 ohm. Dalam Rajah. 7.5 membentangkan keputusan. Sekarang kita boleh menetapkan bahawa graf pertama mewakili harmonik asas, yang kedua - harmonik kedua, dan yang ketiga - hasil penambahannya dalam perintang r. Sudah tentu, adalah mungkin untuk mendapatkan graf V(3) dan bukannya I(r). Dalam kes ini, paksi Y akan ditandakan dalam unit voltan, bukan arus. Pastikan jumlah dua lengkung pertama memberikan lengkung ketiga pada titik masa yang berbeza. Untuk menjadikan plot lebih padat, kami menggunakan offset 1 V untuk asas dan 0.5 V untuk harmonik kedua. Malah, asas mempunyai offset sifar.

nasi. 7.5. Harmonik asas dan kedua dan hasil penambahannya

herotan harmonik kedua dalam penguat

Apabila julat pengendalian penguat melangkaui bahagian linear tindak balas, ia mengakibatkan beberapa herotan. Penghampiran pertama kepada keluk keluaran sebenar dicapai dengan memasukkan harmonik kedua dalam model, menunjukkan bahawa fungsi peralihan berkaitan Kad Pengenalan Dan i b(pengumpul dan arus asas) ialah sejenis parabola. Biasanya herotan adalah lebih rendah daripada yang diandaikan dalam contoh pengenalan pertama kami, yang ditunjukkan dalam Rajah. 7.1. Polinomial yang lebih tepat diberikan oleh formula

f(x) = 0,1 + x + 0,2x².

Adalah memadai untuk mengubah fail input asal untuk menggambarkan keadaan ini. Arahan input untuk sumber bergantung E akan mengambil borang:

E 2 0 poli(1) 1.0 0.1 1 0.2; tiga nilai terakhir untuk k0, k1, k2

dan keseluruhan fail input ialah:

Lakukan analisis dan dapatkan graf V(1) dan V(2) dalam Probe. Anda akan melihat bahawa kedua-dua gelombang kelihatan seperti gelombang sinus sebenar. Untuk perbandingan yang lebih tepat, alih keluar graf V(2) dan dapatkan graf V(2)–0.1. Ini akan merapatkan kedua-dua keluk. Apabila membandingkan gelombang, ingat bahawa V(1) hanyalah gelombang sinus, dan V(2) ialah gabungan harmonik asas dan kedua. Dalam contoh ini, harmonik kedua adalah jauh lebih kecil dalam amplitud daripada yang sebelumnya. Anda boleh mencetak hasil kajian yang ditunjukkan dalam Rajah. 7.6.

nasi. 7.6. Harmonik asas dan kedua dan hasil penambahannya

Selepas keluar dari Probe, lihat fail output untuk kes ini. Voltan input V(1) adalah sama seperti contoh sebelumnya, tetapi V(2) sudah tentu berbeza. Sila ambil perhatian bahawa komponen DC voltan keluaran ialah 0.2 V, dan harmonik kedua pada f=2 kHz mempunyai amplitud 0.1 V dan sudut fasa -90°. Harmonik lain jauh lebih kecil dan boleh diabaikan. Akhir sekali, tentukan jumlah herotan harmonik, iaitu hampir 10%, seperti yang dijangkakan. herotan harmonik kedua ditakrifkan sebagai b 1 /b 2 di mana b 1 dan b 2 - pekali untuk harmonik kedua dan asas, masing-masing. Data ini ditunjukkan dalam Rajah. 7.7.

Analisis Fourier; Herotan Harmonik Kedua, Penguat Kuasa

NOD VOLTAGE NOD VOLTAGE NOD VOLTAGE NOD VOLTAGE

EMPAT KOMPONEN RESPON ANTARA V(1)

KEKERAPAN HARMONIK EMPAT FASA BIASA DIBIASAKAN

NO (HZ) KOMPONEN KOMPONEN (DEG) FASA (DEG)

1 1.000E+03 1.000E+00 1.000E+00 1.115E-06 0.000E+00

2 2.000E+03 1.994E-08 1.994E-08 -9.308E+01 -9.308E+01

3 3.000E+03 7.381E-09 7.381E-09 -9.083E+01 -9.083E+01

4 4.000E+03 4.388E-09 4.388E-09 -8.993E+01 -8.993E+01

5 5.000E+03 3.134E-09 3.134E-09 -9.107E+01 -9.107E+01

6 6.000E+03 1.525E-09 1.525E-09 -6.706E+01 -6.706E+01

7 7.000E+03 1.511E-09 1.511E-09 -1.392E+02 -1.392E+02

8 8.000E+03 1.237E-09 1.237E-09 -3.990E+01 -3.990E+01

9 9.000E+03 7.642E-10 7.642E-10 3.320E+01 3.320E+01

JUMLAH DISTOR HARMONIK = 2.208405E-06 PERATUS

EMPAT KOMPONEN RESPON ANTARA V(2)

KEKERAPAN HARMONIK EMPAT FASA BIASA DIBIASAKAN

NO (HZ) KOMPONEN KOMPONEN (DEG) FASA (DEG)

1 3.000E+03 1.000E+00 1.000E+00 7.683E-07 0.000E+00

2 2.000E+03 1.000E-01 1.000E-01 -9.000E+01 -9.000E+01

3 3.000E+03 1.756E-08 1.756E-08 -1.336E+02 -1.336E+02

4 4.000E+03 1.430E-08 1.430E-08 -1.348E+02 -1.348E+02

5 5.000E+03 9.547E-09 9.547E-09 -1.365E+02 -1.365E+02

6 6.000E+03 8.100E-09 8.100E-09 -1.232E+02 -1.232E+02

7 7.000E+03 6.463E-09 6.463E-09 -1.342E+02 -1.342E+02

8 8.000E+03 5.743E-09 5.743E-09 -9.544E+01 -9.544E+01

9 9.000E+03 6.931E-09 6.931E-09 -1.092E+02 -1.092E+02

JUMLAH DISTORSI HARMONIK = 9.999880E+00 PERATUS

nasi. 7.7. Keputusan analisis herotan pada harmonik kedua dalam penguat

herotan intermodulasi

Kami menggunakan rajah ringkas (Rajah 7.8) untuk menunjukkan bagaimana dua gelombang sinus digabungkan dalam peranti tak linear menggunakan frekuensi yang agak hampir antara satu sama lain, iaitu f 1 =1 kHz dan f 2 =1.5 kHz. Pencampuran tak linear berlaku dalam sumber bergantung jenis e VCVS (INUN). Polinomial yang menerangkan perhubungan mengandungi lebih banyak istilah daripada contoh sebelumnya:

f(x) = 1 + x + X² + x³.

nasi. 7.8. Litar untuk menunjukkan herotan intermodulasi

Arus, merumuskan, mencipta masuk R= Voltan 1 Ohm V(1), secara berangka sama dengan arus masuk R. Oleh itu, voltan input V(1) boleh dianggap sebagai voltan dalam pengadun tak linear. Oleh kerana gelombang sinus mempunyai frekuensi yang berbeza, jumlahnya mewakili ayunan berkala yang kompleks dengan frekuensi yang berbeza daripada frekuensi komponen asal (frekuensi degupan). Fail input:

Jalankan simulasi dan dapatkan Probe V(1). Pilih Plot, X-Axis Settings..., User Defined, dan tetapkan julat dari 0 hingga 10 ms untuk mencapai voltan masukan keadaan mantap. Graf ini ditunjukkan dalam Rajah. 7.9. Untuk mengesahkan bahawa ia sebenarnya adalah jumlah komponen harmonik pada frekuensi 1 dan 1.5 kHz, kami memilih Trace, Fourier, bergerak dari domain masa ke domain frekuensi. Sekarang mari kita ubah sempadan di sepanjang paksi X, menetapkan julat frekuensi dari 4 hingga 12 kHz. Pastikan tetapan paksi sepadan dengan frekuensi yang dikehendaki dan amplitud yang dijangkakan. Malah, apabila f=1 kHz voltan ialah 0.991 V, dan pada f=1.5 kHz ia adalah 0.979 V. Jangan lupa bahawa terdapat beberapa ralat pengumpulan dalam sintesis ini. Dalam Rajah. Rajah 7.10 menunjukkan tindak balas frekuensi amplitud yang sepadan.

nasi. 7.9. Voltan keluaran dengan herotan intermodulasi

nasi. 7.10. Komposisi spektrum voltan masukan

Kemudian pilih Trace, End Fourier untuk kembali ke domain masa, keluarkan graf V(1) dan dapatkan graf voltan keluaran pengadun V(2). Ingat bahawa pengadun ialah INUN dengan hubungan polinomial yang ditentukan oleh fungsi f(X). Kebergantungan masa adalah graf yang serupa dengan graf V(1), tetapi apabila diperiksa dengan lebih dekat anda akan mendapati bahawa bentuk voltan adalah berbeza dengan ketara. Beberapa petunjuk boleh diperolehi daripada komposisi harmonik getaran kompleks ini, jadi ia perlu untuk bergerak semula ke domain frekuensi, memilih julat sepanjang paksi X dari 0 hingga 5 kHz. Kami mengesyorkan mencetak spektrum frekuensi untuk kajian lanjut. Analisis teori komponen modulasi frekuensi membolehkan anda meramal dan mengesahkan keputusan analisis pada PSpice. Ambil perhatian bahawa terdapat komponen DC 2 V bersama-sama komponen penting dalam julat dari 0.5 hingga 4.5 kHz (lihat Rajah 7.11 untuk spektrum frekuensi).

nasi. 7.11. Komposisi spektrum voltan keluaran

Penambahan harmonik

Kes paling mudah untuk analisis teori ialah kes pengaruh harmonik pada litar yang terdiri daripada komponen linear seperti perintang, kapasitor dan induktor, dan, seperti yang anda ketahui, tindak balas adalah ayunan harmonik pada frekuensi isyarat input yang sama. Pelbagai penurunan voltan dalam litar juga mewakili ayunan harmonik dengan frekuensi yang sama, hanya berbeza dalam amplitud dan fasa. Mari kita gunakan gambar rajah mudah untuk menggambarkan beberapa sifat ini. Dalam Rajah. Rajah 7.12 menunjukkan tiga punca voltan membekalkan litar yang mengandungi perintang. R= 1 ohm dan R 1 =R 2 =0.001 Ohm. Dua perintang terakhir diperlukan untuk menjadikan sumber voltan tidak ideal. Menggunakan rajah ini kita boleh menunjukkan penambahan gelombang sinus dalam Probe. Fail input:

Penambahan Gelombang Sinus dengan Frekuensi Yang Sama

*Susunan parameter dalam ungkapan kompleks untuk harmonik

*komponen: offset, amplitud, kekerapan, kelewatan, pengecilan, fasa

v2 2 0 sin(0 1 1kHz 0 0 45); fasa = 45 darjah

v3 3 0 sin(0 1 1kHz 0 0 90); fasa = 90 darjah

nasi. 7.12. Litar untuk menambah isyarat harmonik dengan frekuensi yang sama

Jalankan simulasi dan dapatkan plot v(1), v(2), dan v=v(1)+v(2) dalam Probe. Graf yang terhasil menunjukkan voltan v 2 dengan ketinggalan maksimum kira-kira 45° daripada maksimum v 1, dan jumlah voltan v 1 +v 2 dengan maksimum terletak di antara nilai maksimumnya. Pastikan maksimum v 1 =1 V dicapai pada 251 µs (90°), maksimum v 2 =1 V - pada 131 µs (47.16°) dan maksimum v 1 +v 2 =1.8381 V - pada saat 171 μs (61.56°). Keluarkan graf ini dan dapatkan pergantungan masa untuk kombinasi voltan lain, seperti v(1), v(3) dan v(1)+v(3). Berdasarkan keupayaan anda untuk menambah vektor voltan, cuba ramalkan nilai amplitud untuk jumlah voltan sebelum menghasilkan plot Probe yang ditunjukkan dalam Rajah 1. 7.13.

nasi. 7.13. Hasil penambahan isyarat harmonik dengan frekuensi yang sama

Penambahan harmonik asas dan kedua

Dalam fail input yang sepadan dengan rajah dalam Rajah. 7.12, anda boleh mengubah parameter dan komposisi bekalan kuasa dengan mudah. Mari padam v 3 dan dua kali ganda frekuensi voltan v 2 supaya ia menjadi frekuensi harmonik kedua untuk v 1 . Sudah tentu, ayunan yang terhasil akan serta-merta menjadi bukan sinusoidal. Malah, bentuknya akan bergantung kepada nisbah sudut fasa v 1 dan v 2. Dalam contoh yang sedang dipertimbangkan, biarkan kedua-dua harmonik mencapai maksimum secara serentak. Fail input untuk kes ini:

Menambah Gelombang Biru; Fundamental dan Harmonik Kedua Memuncak Bersama

Jalankan simulasi dan dapatkan graf v(1), v(2), dan v=v(1)+v(2) dalam Probe. Kerana ia v 1 dan v 2 mencapai maksimum pada masa yang sama, maksimum ayunan yang terhasil ialah 2 V, tetapi apabila asas mencapai maksimum negatif, harmonik kedua kembali kepada maksimum positif dan jumlahnya menjadi sifar. Jelaslah bahawa jumlah turun naik ( v 1 +v 2) bukan sinusoidal. Graf ini ditunjukkan dalam Rajah. 7.14.

nasi. 7.14. Hasil penambahan harmonik pertama dan kedua

Modulasi amplitud

Plot ayunan termodulat amplitud yang menarik boleh dihasilkan dalam PSpice dengan menggunakan fungsi mendarab ayunan harmonik dengan frekuensi yang berbeza dengan ketara. Dalam Rajah. Rajah 7.15 menunjukkan gambar rajah yang mensimulasikan peranti sedemikian. Sumber harmonik pertama ialah v 1 dengan frekuensi 1 kHz. Sumber kedua v 2 mempunyai frekuensi 20 kHz. Pendaraban dijalankan dalam sumber bersandar e, iaitu VCVS. Perintang diperlukan untuk mengelakkan potensi terapung. Fail input:

e 3 0 poli (2) 1.0 2.0 0 0 0 0 1

nasi. 7.15. Pengganda untuk modulasi gelombang sinus

Lima entri terakhir dalam arahan input sumber polinomial: 0 0 0 0 1. Ingat bahawa ini adalah nilai pekali dalam sebutan k 0 , k 1 v 1 , k 2 v 2 , k 3 v 12 dan k 4 v 1 v 2. Semua nilai adalah 0 kecuali k 4 yang sama dengan 1.

Jalankan simulasi dan dapatkan plot v(1) dan v(3) dalam Probe. Komponen harmonik dengan frekuensi 20 kHz sengaja tidak diplot pada graf umum, supaya tidak merumitkan pemahaman proses. Ayunan v(3) yang terhasil mempunyai bentuk klasik ayunan termodulat amplitud. Dalam contoh ini, kedua-dua harmonik input v 1 dan v 2 mempunyai amplitud 1 V. Graf ditunjukkan dalam Rajah. 7.16.

nasi. 7.16. Hasil kajian isyarat termodulat amplitud

Tanpa meninggalkan Probe, tambahkan plot voltan input lain v(2) supaya semua voltan dipaparkan: v(1), v(2) dan v(3). Graf ini kini mengandungi, bersama-sama dengan dua gelombang lain, gelombang pembawa, memberikan imej yang lengkap. Dapatkan cetakan untuk kajian lanjut, kemudian padamkan graf v(2) dan pilih Trace, Fourier. Pasang di sepanjang paksi X had julat dari 0 hingga 30 kHz. Domain frekuensi kini memaparkan komponen pada 1.19 dan 21 kHz. Komponen terakhir mewakili frekuensi sisi atas dan bawah yang terhasil daripada modulasi tersebut. Tentukan amplitud bagi setiap gelombang ini. Ingat identiti trigonometri,

(dosa a)(dosa b) = 0.5,

yang menerangkan amplitud 0.5 V untuk frekuensi jalur sisi. Rujuk Rajah. 7.17, yang menunjukkan spektrum frekuensi. (Penanda telah dikeluarkan untuk memberikan gambaran yang lebih jelas.) Lakukan analisis dengan amplitud relatif yang berbeza untuk voltan modulasi v 1 untuk melihat kesannya terhadap kedalaman modulasi T. Sebagai contoh, apabila v 1 mempunyai amplitud 0.8, apakah kedalaman modulasi dan apakah persamaan ayunan yang terhasil?

nasi. 7.17. Spektrum kekerapan ayunan termodulat amplitud

Gambaran keseluruhan arahan PSpice baharu yang digunakan dalam bab ini

.EMPAT <частота>*<выходные переменные>

Sebagai contoh, rekod

menunjukkan bahawa pengembangan siri Fourier dilakukan. Penguraian hanya boleh dilakukan selepas mendapat pergantungan masa untuk keadaan mantap yang diperoleh daripada analisis proses sementara. Perintah ini mesti ada dalam fail input:

TRAN <шаг><момент окончания>

Tugasan

Analisis harmonik memberikan komponen malar harmonik asas, dan semua harmonik sehingga dan termasuk kesembilan. Amplitud dan fasa mereka ditunjukkan dengan nilai sebenar dan relatif. Dalam contoh sebelumnya, V(1) dan V(2) serta komponennya telah dianalisis. Lazimnya, arahan yang digunakan untuk melakukan analisis harmonik ialah .PROBE: bagaimanapun, arahan juga boleh digunakan sebaliknya .CETAKAN atau .PLOT.

7.1. Dalam Rajah. 7.18 polinomial untuk E mempunyai bentuk

f(x) = X + X².

nasi. 7.18

menggunakan v i,puncak=1 V, f=1 kHz dan V= 1 Bandingkan v 0 s v i. Ramalkan anggaran kandungan harmonik voltan keluaran; kemudian jalankan analisis pada PSpice yang akan menunjukkan kandungan harmonik kedua-dua voltan input dan output. Dalam arahan .FOUR, gunakan voltan V(2, 1) dan V(3). Periksa fail keluaran dan tentukan kandungan harmonik V(3).

7.2. Dalam Masalah 7.1, gunakan Trace, Fourier untuk mendapatkan kandungan harmonik V(3). Memaparkan V(2,1) dan V(3), ditetapkan sepanjang paksi X sempadan dari 0 hingga 5 kHz.

7.3. Lakukan analisis untuk masalah 7.1 di

f(x) = 2 + 0,1x².

Ramalkan anggaran kandungan harmonik voltan keluaran; kemudian dapatkan plot V(2,1) dan V(3) untuk menyemak ketepatan ramalan anda.

7.4. Dalam Rajah. Rajah 7.4 menunjukkan sumber polinomial E. Ia diberikan sebagai

f(X) = 1 + X + X².

Gantikan polinomial dengan

f(X) = X + X²,

dan melakukan sintesis dan penguraian dengan menukar i 1 dan i 2 supaya arus I(r) mengikut bentuk voltan V(2).

7.5. Dalam bahagian "Herohan Harmonik Kedua dalam Penguat" dalam bab ini, gantikan polinomial dengan yang berikut:

f(X) = 0,05 + X + 0,1X²,

dan lakukan analisis pada PSpice seperti yang dicadangkan dalam teks. Dapatkan plot V(1) dan (V)2–0.05 untuk membandingkan komponen AC bagi voltan masukan dan keluaran. Ramalkan komponen DC voltan keluaran, amplitud dan fasa harmonik kedua, dan herotan harmonik jumlah. Uji ramalan anda terhadap keputusan Probe dan fail output.

7.6. Dalam bahagian Herotan Intermodulasi, kami menggabungkan dua gelombang sinus dengan frekuensi yang berbeza. Lakukan analisis pada frekuensi f 1 =2 kHz dan f 2 = 2.5 kHz, meninggalkan ungkapan untuk f(X) tanpa perubahan. Ubah suai arahan .TRAN agar sesuai dengan keperluan anda. Lakukan operasi dalam susunan yang sama seperti dalam contoh teks untuk menguji ramalan anda tentang kandungan harmonik voltan keluaran.

7.7. Dalam bahagian "Tambahan harmonik" dalam Rajah. Rajah 7.12 menunjukkan cawangan selari dengan tiga punca voltan. Penambahan harmonik adalah lebih matematik daripada fizikal. Tukar litar supaya semua sumber voltan berada dalam siri, kemudian jalankan analisis semula. Adakah anda mendapat keputusan yang sama?

7.8. Lakukan analisis untuk menambah voltan harmonik berikut dengan frekuensi yang sama f=1 kHz:

v 1 = 0.5∠0°V, v 2 =1∠45°V dan v 23 =1.5∠90° V.

Di mana:

a) Cari nilai maksimum ( v 1 +v 2), serta momen masa dan sudut fasa di mana maksimum dicapai.

b) Ulang langkah a) untuk ( v 1 +v 3).

Apabila menggunakan mod kursor dan berbilang graf pada skrin yang sama, gunakan kekunci [ Ctrl] dan anak panah ← dan → untuk memilih graf yang mana kursor harus bergerak bersama.

7.9. Untuk menggambarkan kesan penambahan harmonik dengan frekuensi yang sama, lakukan analisis seperti dalam Masalah 7.8 untuk set parameter berikut: v 1 =1∠0° V, f 1 =1 kHz, v 1 =1∠0° V, f 2 =1.2 kHz, v 1 =1∠0° V dan f 3 =1.4 kHz:

a) Dapatkan graf v 1 , v 2 dan ( v 1 +v 2). Cari nilai maksimum ( v 1 +v 2).

b) Dapatkan graf v 1 , v 3 dan ( v 1 +v 3). Cari nilai maksimum ( v 1 +v 3).

7.10. Selesaikan masalah daripada bahagian modulasi amplitud dengan meletakkan v 1 =1 V pada 1 kHz, dan berubah v 1 supaya kedalaman modulasi ialah 0.5. Jalankan analisis pada PSpice untuk menunjukkan hasil anda.

Transformasi Fourier ialah cara yang paling banyak digunakan untuk mengubah fungsi masa yang sewenang-wenangnya kepada satu set komponen frekuensinya dalam satah nombor kompleks. Transformasi ini boleh digunakan pada fungsi aperiodik untuk menentukan spektrumnya, dalam hal ini operator kompleks s boleh digantikan dengan /co:

Penyepaduan berangka pada satah kompleks boleh digunakan untuk menentukan frekuensi yang paling menarik.

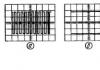
Untuk membiasakan diri dengan tingkah laku asas kamiran ini, mari kita pertimbangkan beberapa contoh. Dalam Rajah. Rajah 14.6 (kiri) menunjukkan nadi luas unit dalam domain masa dan komposisi spektrumnya; di tengah - nadi kawasan yang sama, tetapi dengan amplitud yang lebih besar, dan di sebelah kanan - amplitud nadi adalah tidak terhingga, tetapi kawasannya masih sama dengan perpaduan. Gambar yang betul amat menarik kerana spektrum nadi lebar sifar mengandungi semua frekuensi dengan amplitud yang sama.

nasi. 14.6. Spektrum denyutan dengan lebar yang sama, sepanjang arah yang sama

Pada tahun 1822, ahli matematik Perancis J. B. J. Fourier menunjukkan dalam kerjanya mengenai kekonduksian terma bahawa sebarang fungsi berkala boleh diuraikan kepada komponen awal, termasuk kekerapan ulangan dan set harmonik frekuensi ini, setiap harmonik mempunyai amplitud dan fasa sendiri berkenaan dengan kekerapan ulangan. Rumus asas yang digunakan dalam transformasi Fourier ialah:

di mana A() mewakili komponen arus terus, dan A p dan B p ialah harmonik bagi frekuensi asas susunan dan, yang masing-masing berada dalam fasa dan antifasa dengannya. Oleh itu, fungsi /(*) ialah hasil tambah harmonik dan Lo-

Dalam kes di mana f(x) adalah simetri berkenaan dengan mc/2, i.e. f(x) pada rantau dari l hingga 2l = -f(x) pada rantau dari 0 hingga l, dan tiada komponen arus terus, formula transformasi Fourier dipermudahkan kepada:

di mana n = 1, 3.5, 7…

Semua harmonik adalah sinusoid, hanya sebahagian daripadanya dalam fasa, dan ada yang keluar dari fasa dengan frekuensi asas. Kebanyakan bentuk gelombang yang terdapat dalam elektronik kuasa boleh diselesaikan menjadi harmonik dengan cara ini.

Jika penjelmaan Fourier digunakan pada denyutan segi empat tepat dengan tempoh 120°, maka harmonik akan menjadi satu set tertib k = bi ± 1, di mana n ialah salah satu daripada integer. Amplitud setiap h harmonik berbanding yang pertama dikaitkan dengan nombornya dengan hubungan h = l//e. Dalam kes ini, harmonik pertama akan mempunyai amplitud 1.1 kali lebih besar daripada amplitud isyarat segi empat tepat.

Transformasi Fourier menghasilkan nilai amplitud bagi setiap harmonik, tetapi kerana kesemuanya adalah sinusoidal, nilai RMS diperoleh hanya dengan membahagikan amplitud yang sepadan dengan punca 2. Nilai RMS bagi isyarat kompleks ialah punca kuasa dua hasil tambah kuasa dua nilai RMS setiap harmonik, termasuk yang pertama.

Apabila bekerja dengan fungsi nadi berulang, adalah berguna untuk mempertimbangkan kitaran tugas. Jika denyutan berulang dalam Rajah. 14.7 mempunyai nilai punca-min-kuasa dua X untuk masa A, maka nilai punca-min-kuasa dua untuk masa B akan bersamaan dengan X(A/B) 1 ‘ 2. Oleh itu, nilai rms bagi denyutan berulang adalah berkadar dengan punca kuasa dua nilai kitaran tugas. Menggunakan prinsip ini pada denyutan segi empat tepat dengan tempoh 120° (kitaran tugas 2/3) dengan amplitud kesatuan, kita memperoleh nilai rms (2/3) 1/2 = 0.8165.

nasi. 14.7. Menentukan nilai akar min kuasa dua (RMS) untuk berulang

impuls

Adalah menarik untuk menyemak keputusan ini dengan menjumlahkan harmonik yang sepadan dengan urutan denyutan segi empat tepat yang disebutkan. Dalam Jadual. 14.2 menunjukkan keputusan penjumlahan ini. Seperti yang anda lihat, semuanya sepadan.

Jadual 14.2. Keputusan penjumlahan harmonik sepadan

isyarat berkala dengan kitaran tugas 2/3 dan amplitud unit

Nombor harmonik

Amplitud harmonik

Jumlah nilai RMS

Untuk tujuan perbandingan, sebarang set harmonik boleh dikumpulkan dan tahap herotan harmonik keseluruhan yang sepadan boleh ditentukan. Nilai kuasa dua punca bagi isyarat ditentukan oleh formula

dengan h\ ialah amplitud harmonik pertama (asas), dan h„ ialah amplitud harmonik tertib n > 1.

Komponen yang bertanggungjawab untuk herotan boleh ditulis secara berasingan sebagai

di mana n > 1. Kemudian

di mana Dana ialah harmonik pertama, dan faktor herotan tak linear (THD) akan sama dengan D/Dana.

Walaupun analisis kereta api gelombang persegi menarik, ia jarang digunakan dalam dunia nyata. Kesan pensuisan dan proses lain menjadikan denyutan segi empat tepat lebih seperti denyutan trapezoid, atau, dalam kes penukar, dengan kelebihan hadapan diterangkan oleh 1 cos(0) dan tepi jatuh yang diterangkan oleh cos(0), dengan 0< 0

pada skala logaritma, kecerunan bahagian yang sepadan dalam graf ini ialah -2 dan -1. Untuk sistem dengan nilai reaktans biasa, perubahan dalam cerun lebih kurang berlaku pada frekuensi dari harmonik ke-11 hingga ke-35 frekuensi rangkaian, dan dengan peningkatan dalam reaktans atau arus dalam sistem, kekerapan perubahan dalam cerun berkurangan. Hasil praktikal semua ini ialah harmonik yang lebih tinggi adalah kurang penting daripada yang anda fikirkan.

Walaupun meningkatkan reaktans membantu mengurangkan harmonik tertib tinggi, ini biasanya tidak boleh dilaksanakan. Adalah lebih baik untuk mengurangkan komponen harmonik dalam arus yang digunakan dengan meningkatkan bilangan denyutan semasa pembetulan atau penukaran voltan, yang dicapai dengan peralihan fasa. Berhubung dengan transformer, topik ini telah disentuh dalam Bab. 7. Jika penukar thyristor atau penerus dikuasakan daripada belitan pengubah yang disambungkan dalam bintang dan delta, dan output penukar atau penerus disambungkan secara bersiri atau selari, maka pembetulan 12 nadi diperolehi. Nombor harmonik dalam set kini ialah k = \2n ± 1 dan bukannya k = 6 dan + 1, dengan n ialah salah satu daripada integer. Daripada harmonik tertib ke-5 dan ke-7, harmonik tertib ke-11 dan ke-13 kini muncul, amplitud yang jauh lebih kecil. Ia agak mungkin untuk menggunakan lebih banyak denyutan, dan, sebagai contoh, bekalan kuasa besar untuk loji elektrokimia menggunakan sistem 48-nadi. Oleh kerana penerus dan penukar besar menggunakan set diod atau thyristor yang disambung secara selari, kos tambahan belitan peralihan fasa dalam pengubah sebahagian besarnya menentukan harganya. Dalam Rajah. Rajah 14.8 menunjukkan kelebihan litar 12 nadi berbanding litar 6 nadi. Harmonik tertib ke-11 dan ke-13 dalam litar 12 nadi mempunyai nilai amplitud tipikal kira-kira 10% daripada harmonik pertama. Dalam litar dengan bilangan riak yang banyak, harmonik adalah tertib k = pn + 1, di mana p ialah bilangan riak.

Untuk kepentingan, kami ambil perhatian bahawa pasangan set harmonik yang hanya dianjakkan relatif kepada satu sama lain sebanyak 30° tidak membatalkan satu sama lain dalam litar 6pulse. Arus harmonik ini mengalir balik melalui pengubah; oleh itu, anjakan fasa tambahan diperlukan untuk membolehkan kemusnahan bersama mereka.

Tidak semua harmonik berada dalam fasa dengan yang pertama. Sebagai contoh, dalam corak harmonik tiga fasa sepadan dengan kereta api gelombang persegi 120°, fasa harmonik berubah mengikut urutan -5, +7, -11, +13, dsb. Apabila tidak seimbang dalam litar tiga fasa, komponen fasa tunggal boleh muncul, yang memerlukan tiga kali ganda harmonik dengan anjakan fasa sifar.

nasi. 14.8. Spektrum penukar denyutan 6 dan 12

Transformer pengasingan sering dilihat sebagai ubat penawar untuk masalah harmonik. Transformer ini menambah beberapa reaktans pada sistem dan dengan itu membantu mengurangkan tahap harmonik yang lebih tinggi, bagaimanapun, selain daripada menekan arus jujukan sifar dan penyahgandingan elektrostatik, ia tidak banyak digunakan.

Dalam bab sebelumnya kita telah diperkenalkan kepada sudut pandangan lain mengenai sistem berayun. Kami telah melihat bahawa pelbagai harmonik semula jadi timbul dalam rentetan dan bahawa sebarang getaran tertentu yang boleh diperolehi daripada keadaan awal boleh dianggap sebagai gabungan beberapa harmonik semula jadi yang berayun serentak, yang terdiri dalam perkadaran yang betul. Untuk rentetan, kami mendapati bahawa harmonik semula jadi mempunyai frekuensi ω 0, 2ω 0, Зω 0, .... Oleh itu, gerakan rentetan yang paling umum terdiri daripada ayunan sinusoidal frekuensi asas ω 0, kemudian harmonik kedua 2ω 0, kemudian harmonik ketiga 3ω 0, dsb. Harmonik asas diulang selepas setiap tempoh T 1 = 2π/ω 0, harmonik kedua - selepas setiap tempoh T 2 =2π/2ω 0 ; ia berulang Juga dan selepas setiap haid T 1 =2T 2 , iaitu selepas dua haid mereka. Dengan cara yang sama selepas haid T 1 Harmonik ketiga juga diulang. Segmen ini mengandungi tiga tempohnya. Dan sekali lagi kita faham mengapa tali yang dipetik selepas tempoh T 1 mengulang sepenuhnya bentuk pergerakannya. Beginilah bunyi muzik dihasilkan.

Setakat ini kita telah bercakap tentang pergerakan tali. Namun begitu bunyi, yang mewakili pergerakan udara yang disebabkan oleh pergerakan rentetan, juga mesti terdiri daripada harmonik yang sama, walaupun di sini kita tidak lagi boleh bercakap tentang harmonik udara itu sendiri. Di samping itu, kekuatan relatif pelbagai harmonik di udara mungkin sangat berbeza daripada rentetan, terutamanya jika rentetan itu "disambungkan" ke udara melalui "papan bunyi". Harmonik yang berbeza berkaitan dengan udara dengan cara yang berbeza.

Jika untuk nada muzik fungsinya f(t) mewakili tekanan udara sebagai fungsi masa (katakan, seperti dalam Rajah 50.1,6), maka kita boleh menjangkakan bahawa f(t) ditulis sebagai jumlah bilangan tertentu fungsi harmonik masa (serupa dengan cos ω t) bagi setiap frekuensi harmonik yang berbeza. Jika tempoh ayunan adalah sama dengan T, maka frekuensi sudut asas ialah ω=2π/T, dan harmonik berikut ialah 2ω, 3ω, dsb.

Di sinilah sedikit komplikasi timbul. Kami tidak berhak untuk menjangkakan bahawa untuk setiap kekerapan fasa awal semestinya akan sama antara satu sama lain. Oleh itu, anda perlu menggunakan fungsi seperti cos (ωt + φ) - Sebaliknya, bagaimanapun, ia lebih mudah digunakan untuk setiap satu frekuensi sinus dan kosinus. Biar kami ingatkan anda itu

dan oleh kerana φ ialah pemalar, maka mana-mana ayunan sinusoidal dengan frekuensi co boleh ditulis sebagai jumlah sebutan, satu daripadanya termasuk sin ωt, dan satu lagi termasuk cos ωt.

Jadi kita sampai pada kesimpulan bahawa mana-mana fungsi berkala f(t) dengan period T secara matematik boleh ditulis sebagai

di mana ω=2π/T, A A Dan b - pemalar berangka yang menunjukkan berat setiap komponen getaran dimasukkan ke dalam getaran keseluruhan f(t). Untuk keluasan yang lebih besar, kami menambah istilah dengan kekerapan sifar a 0 pada formula kami, walaupun ia biasanya sama dengan sifar untuk nada muzik. Ini hanyalah anjakan dalam nilai tekanan bunyi purata (iaitu, anjakan dalam tahap "sifar"). Dengan istilah ini formula kami sah untuk sebarang kes. Persamaan (50.2) ditunjukkan secara skematik dalam FIG. 50.2. Amplitud fungsi harmonik An Dan bn dipilih mengikut peraturan khas. Dalam rajah mereka ditunjukkan hanya secara skematik dan bukan mengikut skala. [Siri (50.2) dipanggil berhampiran Fourier untuk fungsi f(t).]

Kami berkata begitu mana-mana Fungsi berkala boleh ditulis dalam bentuk ini. Adalah perlu untuk membuat pindaan kecil dan menekankan bahawa sebarang gelombang bunyi atau mana-mana fungsi yang kita hadapi dalam fizik boleh dikembangkan menjadi siri sedemikian. Ahli matematik, sudah tentu, boleh menghasilkan fungsi yang tidak boleh terdiri daripada harmonik mudah (contohnya, fungsi yang "membungkus" ke belakang, supaya untuk beberapa kuantiti t ia mempunyai dua maksud!). Walau bagaimanapun, kami tidak perlu risau tentang ciri sedemikian di sini.

Dalam banyak kes, tugas untuk mendapatkan (mengira) spektrum isyarat kelihatan seperti ini. Terdapat ADC yang, dengan frekuensi pensampelan Fd, menukar isyarat berterusan yang tiba pada inputnya pada masa T kepada sampel digital - kepingan N. Seterusnya, susunan sampel dimasukkan ke dalam program tertentu yang menghasilkan N/2 daripada beberapa nilai berangka (pengaturcara yang mencuri dari Internet menulis program, memastikan ia melakukan transformasi Fourier).

Untuk menyemak sama ada atur cara berfungsi dengan betul, kami akan membentuk tatasusunan sampel sebagai jumlah dua sinusoid sin(10*2*pi*x)+0.5*sin(5*2*pi*x) dan masukkannya ke dalam atur cara . Program ini menarik perkara berikut:

Rajah.1 Graf fungsi masa isyarat

Rajah.2 Graf spektrum isyarat

Pada graf spektrum terdapat dua batang kayu (harmonik) 5 Hz dengan amplitud 0.5 V dan 10 Hz dengan amplitud 1 V, semuanya sama seperti dalam formula isyarat asal. Semuanya baik-baik saja, pengaturcara yang baik! Program ini berfungsi dengan betul.

Ini bermakna jika kita menggunakan isyarat sebenar daripada campuran dua sinusoid ke input ADC, kita akan mendapat spektrum yang serupa yang terdiri daripada dua harmonik.

Jumlah, kami sebenar isyarat yang diukur berlangsung selama 5 saat, didigitalkan oleh ADC, iaitu, diwakili diskret dikira, telah diskret tidak berkala julat.

Dari sudut matematik, berapa banyakkah kesilapan yang terdapat dalam frasa ini?

Sekarang pihak berkuasa telah memutuskan, kami memutuskan bahawa 5 saat adalah terlalu lama, mari kita mengukur isyarat dalam 0.5 saat.



Rajah.3 Graf bagi fungsi sin(10*2*pi*x)+0.5*sin(5*2*pi*x) untuk tempoh pengukuran 0.5 saat

Rajah.4 Spektrum fungsi

Sesuatu nampaknya tidak betul! Harmonik 10 Hz dilukis seperti biasa, tetapi bukannya batang 5 Hz, beberapa harmonik pelik muncul. Kami melihat di Internet untuk melihat apa yang berlaku...

Nah, mereka mengatakan bahawa anda perlu menambah sifar pada penghujung sampel dan spektrum akan dilukis seperti biasa.

Rajah 5 Menambah sifar sehingga 5 saat

Rajah.6 Spektrum yang diterima

Ia masih tidak sama seperti pada 5 saat. Kita perlu berurusan dengan teori. Mari pergi ke Wikipedia- sumber ilmu.

2. Fungsi berterusan dan perwakilan siri Fouriernya

Secara matematik, isyarat kami dengan tempoh T saat ialah fungsi tertentu f(x) yang ditentukan pada selang (0, T) (X dalam kes ini ialah masa). Fungsi sedemikian sentiasa boleh diwakili sebagai jumlah fungsi harmonik (sinus atau kosinus) dalam bentuk:

K - nombor fungsi trigonometri (nombor komponen harmonik, nombor harmonik)
T - segmen di mana fungsi ditakrifkan (tempoh isyarat)
Ak ialah amplitud bagi komponen harmonik ke-k,
?k- fasa awal komponen harmonik ke-k

Apakah yang dimaksudkan untuk "mewakili fungsi sebagai jumlah siri"? Ini bermakna dengan menambah nilai komponen harmonik siri Fourier pada setiap titik, kita memperoleh nilai fungsi kita pada ketika ini.

(Lebih tegas lagi, sisihan punca-min-kuasa dua siri daripada fungsi f(x) akan cenderung kepada sifar, tetapi walaupun terdapat penumpuan punca-min-kuasa dua, siri Fourier bagi suatu fungsi, secara amnya, tidak diperlukan untuk menumpu ke arahnya. Lihat https://ru.wikipedia.org/ wiki/Fourier_Series.)

Siri ini juga boleh ditulis sebagai:

(2),
di mana , amplitud kompleks k-th.

Hubungan antara pekali (1) dan (3) dinyatakan dengan formula berikut:

Ambil perhatian bahawa ketiga-tiga perwakilan siri Fourier ini adalah setara sepenuhnya. Kadangkala, apabila bekerja dengan siri Fourier, adalah lebih mudah untuk menggunakan eksponen hujah khayalan dan bukannya sinus dan kosinus, iaitu, menggunakan transformasi Fourier dalam bentuk kompleks. Tetapi adalah mudah untuk kita menggunakan formula (1), di mana siri Fourier dibentangkan sebagai jumlah kosinus dengan amplitud dan fasa yang sepadan. Walau apa pun, adalah tidak betul untuk mengatakan bahawa transformasi Fourier bagi isyarat sebenar akan menghasilkan amplitud harmonik yang kompleks. Seperti yang dikatakan Wiki dengan betul, "Transformasi Fourier (?) ialah operasi yang mengaitkan satu fungsi pembolehubah sebenar dengan fungsi lain, juga pembolehubah nyata."

Jumlah:
Asas matematik untuk analisis spektrum isyarat ialah transformasi Fourier.

Transformasi Fourier membolehkan anda mewakili fungsi berterusan f(x) (isyarat), yang ditakrifkan pada segmen (0, T) sebagai hasil tambah nombor tak terhingga (siri tak terhingga) fungsi trigonometri (sinus dan/atau kosinus) dengan tertentu. amplitud dan fasa, juga dipertimbangkan pada segmen (0, T). Siri sedemikian dipanggil siri Fourier.

Mari kita perhatikan beberapa perkara lagi, pemahaman yang diperlukan untuk aplikasi yang betul bagi transformasi Fourier kepada analisis isyarat. Jika kita menganggap siri Fourier (jumlah sinusoid) pada keseluruhan paksi-X, kita dapat melihat bahawa di luar segmen (0, T) fungsi yang diwakili oleh siri Fourier akan mengulangi fungsi kita secara berkala.

Contohnya, dalam graf Rajah 7, fungsi asal ditakrifkan pada segmen (-T\2, +T\2), dan siri Fourier mewakili fungsi berkala yang ditakrifkan pada keseluruhan paksi-x.

Ini berlaku kerana sinusoid sendiri adalah fungsi berkala, dan dengan itu jumlahnya akan menjadi fungsi berkala.

Rajah.7 Perwakilan fungsi asal bukan berkala oleh siri Fourier

Oleh itu:

Fungsi asal kami adalah berterusan, tidak berkala, ditakrifkan pada segmen tertentu panjang T.
Spektrum fungsi ini adalah diskret, iaitu, ia dibentangkan dalam bentuk siri komponen harmonik yang tidak terhingga - siri Fourier.
Sebenarnya, siri Fourier mentakrifkan fungsi berkala tertentu yang bertepatan dengan fungsi kami pada segmen (0, T), tetapi bagi kami keberkalaan ini tidak penting.

Tempoh bagi komponen harmonik ialah gandaan bagi nilai segmen (0, T) di mana fungsi asal f(x) ditakrifkan. Dalam erti kata lain, tempoh harmonik ialah gandaan tempoh pengukuran isyarat. Sebagai contoh, tempoh harmonik pertama siri Fourier adalah sama dengan selang T di mana fungsi f(x) ditakrifkan. Tempoh harmonik kedua siri Fourier adalah sama dengan selang T/2. Dan seterusnya (lihat Rajah 8).

Rajah 8 Tempoh (frekuensi) komponen harmonik siri Fourier (di sini T = 2?)

Oleh itu, frekuensi komponen harmonik adalah gandaan 1/T. Iaitu, frekuensi komponen harmonik Fk adalah sama dengan Fk = k\T, di mana k berjulat dari 0 hingga?, contohnya k = 0 F0 = 0; k=1 F1=1\T; k=2 F2=2\T; k=3 F3=3\T;… Fk= k\T (pada frekuensi sifar - komponen malar).

Biarkan fungsi asal kita menjadi isyarat yang direkodkan semasa T=1 saat. Kemudian tempoh harmonik pertama akan sama dengan tempoh isyarat kami T1=T=1 saat dan frekuensi harmonik ialah 1 Hz. Tempoh harmonik kedua akan sama dengan tempoh isyarat dibahagikan dengan 2 (T2=T/2=0.5 saat) dan frekuensinya ialah 2 Hz. Untuk harmonik ketiga T3=T/3 saat dan frekuensi ialah 3 Hz. Dan sebagainya.

Langkah antara harmonik dalam kes ini ialah 1 Hz.

Oleh itu, isyarat berpanjangan 1 saat boleh diuraikan kepada komponen harmonik (mendapatkan spektrum) dengan resolusi frekuensi 1 Hz.
Untuk meningkatkan resolusi sebanyak 2 kali kepada 0.5 Hz, anda perlu meningkatkan tempoh pengukuran sebanyak 2 kali - sehingga 2 saat. Isyarat berpanjangan 10 saat boleh diuraikan kepada komponen harmonik (untuk mendapatkan spektrum) dengan resolusi frekuensi 0.1 Hz. Tiada cara lain untuk meningkatkan resolusi frekuensi.

Terdapat cara untuk meningkatkan tempoh isyarat secara buatan dengan menambahkan sifar pada tatasusunan sampel. Tetapi ia tidak meningkatkan resolusi frekuensi sebenar.

3. Isyarat diskret dan transformasi Fourier diskret

Dengan perkembangan teknologi digital, kaedah menyimpan data ukuran (isyarat) juga telah berubah. Jika sebelum ini isyarat boleh dirakam pada perakam pita dan disimpan pada pita dalam bentuk analog, kini isyarat didigitalkan dan disimpan dalam fail dalam ingatan komputer sebagai satu set nombor (sampel).

Skim biasa untuk mengukur dan mendigitalkan isyarat adalah seperti berikut.

Rajah 9 Rajah saluran pengukur

Isyarat daripada transduser pengukur tiba di ADC dalam tempoh masa T. Sampel isyarat (persampelan) yang diperoleh semasa T dihantar ke komputer dan disimpan dalam ingatan.

Rajah 10 Isyarat berdigit - N sampel diterima semasa masa T

Apakah keperluan untuk parameter pendigitalan isyarat? Peranti yang menukar isyarat analog input kepada kod diskret (isyarat digital) dipanggil penukar analog-ke-digital (ADC) (Wiki).

Salah satu parameter utama ADC ialah kekerapan pensampelan maksimum (atau kadar pensampelan, kadar sampel Bahasa Inggeris) - kadar pensampelan isyarat berterusan masa semasa mensampelnya. Ia diukur dalam Hertz. ((Wiki))

Menurut teorem Kotelnikov, jika isyarat berterusan mempunyai spektrum yang dihadkan oleh frekuensi Fmax, maka ia boleh dibina semula sepenuhnya dan unik daripada sampel diskretnya yang diambil pada selang masa, i.e. dengan kekerapan Fd? 2*Fmax, dengan Fd ialah kekerapan pensampelan; Fmax - kekerapan maksimum spektrum isyarat. Dengan kata lain, frekuensi pendigitalan isyarat (frekuensi pensampelan ADC) mestilah sekurang-kurangnya 2 kali lebih tinggi daripada frekuensi maksimum isyarat yang ingin kita ukur.

Apakah yang akan berlaku jika kita mengambil sampel dengan frekuensi yang lebih rendah daripada yang diperlukan oleh teorem Kotelnikov?

Dalam kes ini, kesan "aliasing" berlaku (juga dikenali sebagai kesan stroboskopik, kesan moiré), di mana isyarat frekuensi tinggi, selepas pendigitalan, bertukar menjadi isyarat frekuensi rendah, yang sebenarnya tidak wujud. Dalam Rajah. 5 gelombang sinus frekuensi tinggi merah adalah isyarat sebenar. Sinusoid biru dengan frekuensi yang lebih rendah ialah isyarat rekaan yang timbul kerana fakta bahawa semasa masa pensampelan lebih daripada separuh tempoh isyarat frekuensi tinggi mempunyai masa untuk lulus.

nasi. 11. Kemunculan isyarat frekuensi rendah palsu pada kadar pensampelan yang tidak cukup tinggi

Untuk mengelakkan kesan aliasing, penapis anti-aliasing khas diletakkan di hadapan ADC - penapis laluan rendah (LPF), yang melepasi frekuensi di bawah separuh daripada kekerapan pensampelan ADC, dan memotong frekuensi yang lebih tinggi.

Untuk mengira spektrum isyarat daripada sampel diskretnya, transformasi Fourier diskret (DFT) digunakan. Mari kita ambil perhatian sekali lagi bahawa spektrum isyarat diskret "mengikut takrifan" dihadkan oleh frekuensi Fmax, iaitu kurang daripada separuh frekuensi pensampelan Fd. Oleh itu, spektrum isyarat diskret boleh diwakili oleh jumlah bilangan harmonik terhingga, berbeza dengan jumlah tak terhingga untuk siri Fourier bagi isyarat berterusan, yang spektrumnya boleh tidak terhad. Menurut teorem Kotelnikov, kekerapan maksimum harmonik mestilah sedemikian rupa sehingga menyumbang sekurang-kurangnya dua sampel, oleh itu bilangan harmonik adalah sama dengan separuh bilangan sampel isyarat diskret. Iaitu, jika terdapat N sampel dalam sampel, maka bilangan harmonik dalam spektrum akan sama dengan N/2.

Mari kita pertimbangkan transformasi Fourier diskret (DFT).

Membandingkan dengan siri Fourier

Kami melihat bahawa ia bertepatan, kecuali masa dalam DFT bersifat diskret dan bilangan harmonik dihadkan oleh N/2 - separuh daripada bilangan sampel.

Formula DFT ditulis dalam pembolehubah integer tak berdimensi k, s, dengan k ialah bilangan sampel isyarat, s ialah bilangan komponen spektrum.
Nilai s menunjukkan bilangan ayunan harmonik lengkap sepanjang tempoh T (tempoh pengukuran isyarat). Transformasi Fourier diskret digunakan untuk mencari amplitud dan fasa harmonik menggunakan kaedah berangka, i.e. "pada komputer"

Berbalik kepada keputusan yang diperoleh pada mulanya. Seperti yang dinyatakan di atas, apabila mengembangkan fungsi bukan berkala (isyarat kami) ke dalam siri Fourier, siri Fourier yang terhasil sebenarnya sepadan dengan fungsi berkala dengan tempoh T (Rajah 12).

Rajah 12 Fungsi berkala f(x) dengan tempoh T0, dengan tempoh pengukuran T>T0

Seperti yang boleh dilihat dalam Rajah 12, fungsi f(x) adalah berkala dengan tempoh T0. Walau bagaimanapun, disebabkan oleh fakta bahawa tempoh sampel pengukuran T tidak bertepatan dengan tempoh fungsi T0, fungsi yang diperolehi sebagai siri Fourier mempunyai ketakselanjaran pada titik T. Akibatnya, spektrum fungsi ini akan mengandungi sejumlah besar harmonik frekuensi tinggi. Jika tempoh sampel pengukuran T bertepatan dengan tempoh fungsi T0, maka spektrum yang diperoleh selepas transformasi Fourier hanya akan mengandungi harmonik pertama (sinusoid dengan tempoh yang sama dengan tempoh pensampelan), kerana fungsi f(x) ialah sinusoid.

Dalam erti kata lain, program DFT "tidak tahu" bahawa isyarat kami adalah "sekeping sinusoid", tetapi cuba untuk mewakili fungsi berkala dalam bentuk siri, yang mempunyai ketakselanjaran disebabkan oleh ketidakkonsistenan kepingan individu. sebuah sinusoid.

Akibatnya, harmonik muncul dalam spektrum, yang sepatutnya merumuskan bentuk fungsi, termasuk ketakselanjaran ini.

Oleh itu, untuk mendapatkan spektrum isyarat yang "betul", yang merupakan jumlah beberapa sinusoid dengan tempoh yang berbeza, adalah perlu bahawa nombor integer tempoh bagi setiap sinusoid sesuai dengan tempoh pengukuran isyarat. Dalam amalan, keadaan ini boleh dipenuhi untuk tempoh pengukuran isyarat yang cukup lama.

Rajah 13 Contoh fungsi dan spektrum isyarat ralat kinematik kotak gear

Dengan tempoh yang lebih pendek, gambar akan kelihatan "lebih teruk":

Rajah 14 Contoh fungsi dan spektrum isyarat getaran rotor

Dalam amalan, sukar untuk memahami di manakah "komponen sebenar" dan di manakah "artifak" yang disebabkan oleh tempoh bukan berbilang komponen dan tempoh pensampelan isyarat atau "melompat dan pecah" dalam bentuk isyarat . Sudah tentu, perkataan "komponen sebenar" dan "artifak" diletakkan dalam tanda petikan atas sebab tertentu. Kehadiran banyak harmonik pada graf spektrum tidak bermakna isyarat kita sebenarnya "terdiri" daripadanya. Ini sama seperti berfikir bahawa nombor 7 "terdiri" daripada nombor 3 dan 4. Nombor 7 boleh diwakili sebagai jumlah nombor 3 dan 4 - ini betul.

Jadi isyarat kami... atau lebih tepatnya bukan "isyarat kami", tetapi fungsi berkala yang digubah dengan mengulangi isyarat kami (persampelan) boleh diwakili sebagai jumlah harmonik (gelombang sinus) dengan amplitud dan fasa tertentu. Tetapi dalam banyak kes yang penting untuk latihan (lihat rajah di atas), sememangnya mungkin untuk mengaitkan harmonik yang diperolehi dalam spektrum dengan proses sebenar yang bersifat kitaran dan memberi sumbangan penting kepada bentuk isyarat.

Beberapa keputusan

1. Isyarat terukur sebenar dengan tempoh T saat, didigitalkan oleh ADC, iaitu, diwakili oleh set sampel diskret (N keping), mempunyai spektrum bukan berkala diskret, diwakili oleh set harmonik (N/ 2 keping).

2. Isyarat diwakili oleh satu set nilai sebenar dan spektrumnya diwakili oleh satu set nilai sebenar. Frekuensi harmonik adalah positif. Hakikat bahawa lebih mudah bagi ahli matematik untuk mewakili spektrum dalam bentuk kompleks menggunakan frekuensi negatif tidak bermakna bahawa "ini betul" dan "ini harus sentiasa dilakukan."

3. Isyarat yang diukur dalam selang masa T ditentukan hanya dalam selang masa T. Apa yang berlaku sebelum kita mula mengukur isyarat, dan apa yang akan berlaku selepas itu, tidak diketahui oleh sains. Dan dalam kes kami, ia tidak menarik. DFT bagi isyarat terhad masa memberikan spektrum "benar", dalam erti kata, dalam keadaan tertentu, ia membolehkan seseorang mengira amplitud dan kekerapan komponennya.

Bahan yang digunakan dan bahan lain yang berguna.