Kaedah penggandaLagrange(dalam kesusasteraan Inggeris “Kaedah pengganda tidak ditentukan LaGrange”) ˗ ialah kaedah berangka untuk menyelesaikan masalah pengoptimuman yang membolehkan anda menentukan ekstrem “bersyarat” Fungsi objektif(nilai minimum atau maksimum)

dengan adanya sekatan tertentu pada pembolehubahnya dalam bentuk kesamaan (iaitu, kawasan nilai yang boleh diterima)

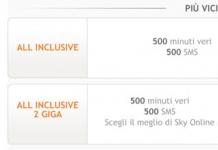
˗ ini ialah nilai argumen fungsi (parameter boleh dikawal) pada domain sebenar di mana nilai fungsi cenderung kepada ekstrem. Penggunaan nama ekstrem "bersyarat" adalah disebabkan oleh fakta bahawa pembolehubah tertakluk kepada syarat tambahan, yang mengehadkan julat nilai yang boleh diterima apabila mencari ekstrem fungsi.

Kaedah pengganda Lagrange membolehkan masalah mencari ekstrem bersyarat bagi fungsi objektif pada set nilai yang boleh diterima untuk diubah menjadi masalah pengoptimuman tanpa syarat fungsi.

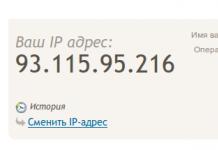
Dalam kes fungsi Dan adalah selanjar bersama derivatif separanya, maka terdapat pembolehubah λ sedemikian yang tidak serentak sama dengan sifar, di mana syarat berikut dipenuhi:

Oleh itu, selaras dengan kaedah pengganda Lagrange, untuk mencari ekstrem fungsi objektif pada set nilai yang boleh diterima, saya menyusun fungsi Lagrange L(x, λ), yang dioptimumkan lagi:

di mana λ ˗ ialah vektor pembolehubah tambahan yang dipanggil pengganda Lagrange tidak ditentukan.

Oleh itu, masalah mencari ekstrem bersyarat bagi fungsi f(x) telah dikurangkan kepada masalah mencari ekstrem tanpa syarat bagi fungsi L(x, λ).

Dan

Syarat yang diperlukan untuk ekstrem fungsi Lagrange diberikan oleh sistem persamaan (sistem terdiri daripada persamaan "n + m"):

Menyelesaikan sistem persamaan ini membolehkan kita menentukan hujah bagi fungsi (X) di mana nilai fungsi L(x, λ), serta nilai fungsi sasaran f(x) sepadan dengan ekstrem.

Magnitud pengganda Lagrange (λ) adalah menarik minat praktikal jika kekangan dibentangkan dalam bentuk dengan sebutan bebas dalam persamaan (malar). Dalam kes ini, kita boleh mempertimbangkan lagi (meningkat/menurun) nilai fungsi objektif dengan menukar nilai pemalar dalam sistem persamaan. Oleh itu, pengganda Lagrange mencirikan kadar perubahan dalam maksimum fungsi objektif apabila pemalar had berubah.

Terdapat beberapa cara untuk menentukan sifat ekstrem bagi fungsi yang terhasil:

Kaedah pertama: Biarkan koordinat titik ekstrem, dan nilai yang sepadan bagi fungsi objektif. Titik yang hampir dengan titik diambil dan nilai fungsi objektif dikira:

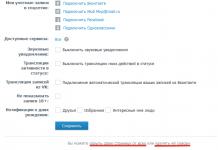
Jika , maka terdapat maksimum pada titik itu.

Jika , maka terdapat minimum pada titik itu.

Kaedah kedua: Keadaan yang mencukupi dari mana sifat ekstrem boleh ditentukan ialah tanda pembezaan kedua fungsi Lagrange. Pembezaan kedua bagi fungsi Lagrange ditakrifkan seperti berikut:

Jika dalam titik yang diberikan minimum, jika , maka fungsi objektif f(x) mempunyai bersyarat maksimum.

Kaedah ketiga: Juga, sifat extremum fungsi boleh ditentukan dengan mempertimbangkan Hessian fungsi Lagrange. Matriks Hessian adalah simetri matriks segi empat sama terbitan separa kedua bagi suatu fungsi pada titik di mana unsur matriks adalah simetri mengenai pepenjuru utama.

Untuk menentukan jenis ekstrem (maksimum atau minimum fungsi), anda boleh menggunakan peraturan Sylvester:

1. Agar pembezaan kedua fungsi Lagrange menjadi tanda positif adalah perlu bahawa minor sudut bagi fungsi itu adalah positif. Di bawah keadaan sedemikian, fungsi pada ketika ini mempunyai minimum.

2. Agar pembezaan kedua fungsi Lagrange menjadi tanda negatif , adalah perlu bahawa minor sudut bagi fungsi itu silih berganti, dan elemen pertama matriks mestilah negatifv. Di bawah keadaan sedemikian, fungsi pada ketika ini mempunyai maksimum.

Dengan kecil bersudut kita maksudkan minor yang terletak di baris k pertama dan lajur k matriks asal.

Asas kepentingan praktikal Kaedah Lagrange ialah ia membolehkan anda beralih daripada pengoptimuman bersyarat kepada pengoptimuman tanpa syarat dan, dengan itu, mengembangkan senjata kaedah yang ada menyelesaikan masalah. Walau bagaimanapun, masalah menyelesaikan sistem persamaan, yang bermuara kepada kaedah ini, secara amnya ia tidak lebih mudah masalah asal mencari ekstrem. Kaedah sedemikian dipanggil tidak langsung. Penggunaannya dijelaskan oleh keperluan untuk mendapatkan penyelesaian kepada masalah yang melampau dalam bentuk analisis (contohnya, untuk pengiraan teori tertentu). Apabila menyelesaikan spesifik masalah praktikal Kaedah langsung biasanya digunakan, berdasarkan proses berulang untuk mengira dan membandingkan nilai fungsi yang dioptimumkan.

Kaedah pengiraan

1 langkah: Kami menentukan fungsi Lagrange daripada fungsi objektif dan sistem kekangan yang diberikan:

ke hadapan

Untuk menambah ulasan anda pada artikel, sila daftar di tapak.

Nama parameter	Maknanya
Topik artikel:	Kaedah Lagrange.
Rubrik (kategori tematik)	Matematik

Mencari polinomial bermakna menentukan nilai pekalinya . Untuk melakukan ini, menggunakan keadaan interpolasi, anda boleh membentuk sistem persamaan algebra linear (SLAE).

Penentu SLAE ini biasanya dipanggil penentu Vandermonde. Penentu Vandermonde bukan sama dengan sifar bila untuk , iaitu, dalam kes apabila tiada nod yang sepadan dalam jadual carian. Walau bagaimanapun, boleh dikatakan bahawa SLAE mempunyai penyelesaian dan penyelesaian ini adalah unik. Setelah menyelesaikan SLAE dan menentukan pekali yang tidak diketahui anda boleh membina polinomial interpolasi.

Polinomial yang memenuhi syarat interpolasi, apabila diinterpolasi dengan kaedah Lagrange, dibina dalam bentuk gabungan linear polinomial darjah ke-n:

Polinomial biasanya dipanggil asas polinomial. Untuk Polinomial Lagrange memenuhi syarat interpolasi, adalah sangat penting bahawa syarat berikut dipenuhi untuk polinomial asasnya:

Untuk .

Jika syarat ini dipenuhi, maka untuk mana-mana yang kami ada:

Selain itu, pemenuhan syarat yang ditentukan untuk polinomial asas bermakna syarat interpolasi juga dipenuhi.

Mari kita tentukan jenis polinomial asas berdasarkan sekatan yang dikenakan ke atasnya.

syarat pertama: di .

syarat kedua: .

Akhirnya, untuk polinomial asas kita boleh menulis:

Kemudian, menggantikan ungkapan yang terhasil untuk polinomial asas kepada polinomial asal, kita memperoleh bentuk akhir polinomial Lagrange:

Borang persendirian Polinomial Lagrange at biasanya dipanggil formula interpolasi linear:

.

Polinomial Lagrange yang diambil biasanya dipanggil formula interpolasi kuadratik:

Kaedah Lagrange. - konsep dan jenis. Klasifikasi dan ciri kategori "Kaedah Lagrange." 2017, 2018.

- Kaedah Lagrange (kaedah variasi pemalar arbitrari).

Kawalan jauh linear. Definisi. jenis DU i.e. linear berkenaan dengan fungsi yang tidak diketahui dan terbitannya dipanggil linear. Untuk penyelesaian jenis ini, kita akan mempertimbangkan dua kaedah: kaedah Lagrange dan kaedah Bernoulli. Pertimbangkan persamaan pembezaan homogen. Persamaan ini adalah dengan pembolehubah boleh diasingkan. Penyelesaian persamaan tersebut ialah Umum... .

- Sistem kawalan linear, homogen dan heterogen. Konsep keputusan umum. Kaedah Lagrange variasi pemalar pengeluaran.

Definisi. Sistem kawalan dipanggil homogen jika fungsi boleh diwakili sebagai hubungan antara hujahnya. Contoh. F dipanggil homogen ukuran kelima jika Contoh: 1) - tertib kehomogenan pertama. 2) - tertib kehomogenan ke-2. 3) - tertib sifar kehomogenan (hanya homogen... .

- Kuliah 8. Aplikasi terbitan separa: masalah ekstrem. Kaedah Lagrange.

Masalah melampau ada sangat penting dalam pengiraan ekonomi. Ini adalah pengiraan, sebagai contoh, pendapatan maksimum, keuntungan, kos minimum bergantung pada beberapa pembolehubah: sumber, aset pengeluaran, dsb. Teori mencari extrema fungsi... .

- T.2.3. DE pesanan yang lebih tinggi. Persamaan dalam jumlah pembezaan. T.2.4. Persamaan pembezaan linear tertib kedua dengan pekali malar. Kaedah Lagrange.

3. 2. 1. DE dengan pembolehubah boleh dipisahkan S.R. 3. Dalam sains semula jadi, teknologi dan ekonomi, seseorang sering perlu berurusan dengan formula empirikal, i.e. formula yang disusun berdasarkan pemprosesan data statistik atau...

Kaedah untuk menentukan ekstrem bersyarat bermula dengan membina fungsi bantu Lagrange, yang dalam kawasan penyelesaian yang boleh dilaksanakan mencapai maksimum untuk nilai pembolehubah yang sama x 1 , x 2 , ..., x n , yang sama dengan fungsi objektif z . Biarkan masalah menentukan ekstrem bersyarat bagi fungsi itu diselesaikan z = f(X) di bawah sekatan φ i ( x 1 , x 2 , ..., x n ) = 0, i = 1, 2, ..., m , m < n

Mari kita karang fungsi

yang dipanggil Fungsi Lagrange. X , - faktor malar ( Pengganda Lagrange). Ambil perhatian bahawa pengganda Lagrange boleh diberikan pengertian ekonomi. Jika f(x 1 , x 2 , ..., x n ) - pendapatan selaras dengan pelan X = (x 1 , x 2 , ..., x n ) , dan fungsi φ i (x 1 , x 2 , ..., x n ) - kos sumber ke-i yang sepadan dengan pelan ini, kemudian X , ialah harga (anggaran) sumber ke-i, mencirikan perubahan dalam nilai ekstrem fungsi objektif bergantung kepada perubahan dalam saiz sumber ke-i (anggaran marginal). L(X) - fungsi n+m pembolehubah (x 1 , x 2 , ..., x n , λ 1 , λ 2 , ..., λ n ) . Menentukan titik pegun bagi fungsi ini membawa kepada penyelesaian sistem persamaan

Ia mudah untuk melihatnya . Oleh itu, tugas mencari ekstrem bersyarat bagi fungsi z = f(X) mengurangkan untuk mencari ekstrem tempatan fungsi L(X) . Sekiranya titik pegun dijumpai, maka persoalan kewujudan ekstrem dalam kes paling mudah diselesaikan berdasarkan syarat yang mencukupi untuk ekstrem - mengkaji tanda pembezaan kedua d 2 L(X) pada titik pegun, dengan syarat pembolehubah bertambah Δx i - dihubungkan oleh perhubungan

diperoleh dengan membezakan persamaan gandingan.

Menyelesaikan sistem persamaan tak linear dalam dua yang tidak diketahui menggunakan alat Cari Penyelesaian

tetapan Mencari penyelesaian membolehkan anda mencari penyelesaian kepada sistem persamaan tak linear dengan dua yang tidak diketahui:

di mana
- fungsi bukan linear pembolehubah x Dan y ,
- pemalar sewenang-wenangnya.

Adalah diketahui bahawa pasangan itu ( x , y ) ialah penyelesaian kepada sistem persamaan (10) jika dan hanya jika ia adalah penyelesaian kepada persamaan berikut dengan dua yang tidak diketahui:

DENGAN sebaliknya, penyelesaian kepada sistem (10) ialah titik persilangan dua lengkung: f ] (x, y) = C Dan f 2 (x, y) = C 2 di permukaan XOY.

Ini membawa kepada kaedah untuk mencari akar sistem. persamaan tak linear:

Tentukan (sekurang-kurangnya lebih kurang) selang kewujudan penyelesaian kepada sistem persamaan (10) atau persamaan (11). Di sini adalah perlu untuk mengambil kira jenis persamaan yang termasuk dalam sistem, domain takrifan setiap persamaannya, dsb. Kadangkala pemilihan anggaran awal penyelesaian digunakan;

Jadualkan penyelesaian kepada persamaan (11) untuk pembolehubah x dan y pada selang yang dipilih, atau bina graf fungsi f 1 (x, y) = C, dan f 2 (x,y) = C 2 (sistem(10)).

Setempatkan punca yang sepatutnya bagi sistem persamaan - cari beberapa nilai minimum daripada jadual, jadualkan punca persamaan (11), atau tentukan titik persilangan lengkung yang termasuk dalam sistem (10).

4. Cari punca bagi sistem persamaan (10) menggunakan tambah Mencari penyelesaian.

Kaedah pengganda Lagrange.

Kaedah pengganda Lagrange adalah salah satu kaedah yang membolehkan anda menyelesaikan masalah tanpa pengaturcaraan linear.

Pengaturcaraan bukan linear ialah satu cabang pengaturcaraan matematik yang mengkaji kaedah untuk menyelesaikan masalah ekstrem dengan fungsi objektif bukan linear dan kawasan penyelesaian yang boleh dilaksanakan yang ditakrifkan oleh kekangan bukan linear. Dalam ekonomi, ini sepadan dengan fakta bahawa hasil (kecekapan) meningkat atau menurun secara tidak seimbang dengan perubahan dalam skala penggunaan sumber (atau, apa yang sama, skala pengeluaran): contohnya, disebabkan oleh pembahagian kos pengeluaran dalam perusahaan kepada berubah-ubah dan separa tetap; disebabkan ketepuan permintaan untuk barangan, apabila setiap unit berikutnya lebih sukar untuk dijual daripada yang sebelumnya, dsb.

Masalah pengaturcaraan tak linear ditimbulkan sebagai masalah mencari optimum bagi fungsi objektif tertentu

F(x 1 ,…x n), F (x) → maks

apabila syarat dipenuhi

g j (x 1 ,…x n)≥0, g (x) ≤ b , x ≥ 0

di mana x-vektor pembolehubah yang diperlukan;

F (x) -Fungsi objektif;

g (x) - fungsi kekangan (boleh dibezakan secara berterusan);

b - vektor pemalar kekangan.

Penyelesaian kepada masalah pengaturcaraan tak linear (maksimum atau minimum global) boleh dimiliki sama ada dalam sempadan atau bahagian dalam set yang boleh diterima.

Tidak seperti masalah pengaturcaraan linear, dalam masalah pengaturcaraan bukan linear, optimum tidak semestinya terletak pada sempadan rantau yang ditakrifkan oleh kekangan. Dalam erti kata lain, tugasnya adalah untuk memilih nilai pembolehubah bukan negatif sedemikian, tertakluk kepada sistem sekatan dalam bentuk ketidaksamaan, di mana maksimum (atau minimum) fungsi tertentu dicapai. Dalam kes ini, bentuk fungsi objektif mahupun ketaksamaan tidak dinyatakan. Boleh jadi kes yang berbeza: fungsi objektif adalah tak linear, dan kekangan adalah linear; fungsi objektif adalah linear, dan kekangan (sekurang-kurangnya satu daripadanya) adalah tidak linear; kedua-dua fungsi objektif dan kekangan adalah tidak linear.

Masalah pengaturcaraan tak linear ditemui dalam sains semula jadi, kejuruteraan, ekonomi, matematik, hubungan perniagaan dan kerajaan.

Pengaturcaraan bukan linear, sebagai contoh, berkaitan dengan asas tugas ekonomi. Jadi dalam masalah pengagihan sumber yang terhad memaksimumkan sama ada kecekapan atau, jika pengguna sedang dikaji, penggunaan di bawah kekangan yang menyatakan keadaan kekurangan sumber. Dalam rumusan umum sedemikian, rumusan matematik masalah mungkin mustahil, tetapi dalam aplikasi khusus bentuk kuantitatif semua fungsi boleh ditentukan secara langsung. Sebagai contoh, perusahaan perindustrian menghasilkan produk plastik. Kecekapan pengeluaran di sini diukur dengan keuntungan, dan kekangan ditafsirkan sebagai buruh yang tersedia, ruang pengeluaran, produktiviti peralatan, dsb.

Kaedah keberkesanan kos juga sesuai dengan skim pengaturcaraan tak linear. Kaedah ini dibangunkan untuk digunakan dalam membuat keputusan dalam kerajaan. Fungsi am kecekapan adalah kesejahteraan. Di sini dua masalah pengaturcaraan tak linear timbul: yang pertama memaksimumkan kesan pada kos terhad, yang kedua meminimumkan kos dengan syarat kesannya melebihi tahap minimum tertentu. Masalah ini biasanya dimodelkan dengan baik menggunakan pengaturcaraan tak linear.

Hasil penyelesaian masalah pengaturcaraan tak linear membantu dalam membuat keputusan kerajaan. Penyelesaian yang terhasil, sudah tentu, disyorkan, jadi adalah perlu untuk memeriksa andaian dan ketepatan masalah pengaturcaraan tak linear sebelum membuat keputusan muktamad.

Masalah bukan linear adalah kompleks; ia sering dipermudahkan dengan membawa kepada masalah linear. Untuk melakukan ini, secara konvensional diandaikan bahawa dalam kawasan tertentu fungsi objektif bertambah atau berkurang mengikut kadar perubahan dalam pembolehubah bebas. Pendekatan ini dipanggil kaedah penghampiran linear sekeping; namun, ia hanya terpakai untuk jenis masalah bukan linear tertentu.

Masalah bukan linear di bawah keadaan tertentu diselesaikan menggunakan fungsi Lagrange: dengan mencari titik pelananya, penyelesaian kepada masalah itu ditemui. Antara algoritma pengiraan N. p. tempat yang bagus menduduki kaedah kecerunan. Tiada kaedah universal untuk masalah tak linear dan, nampaknya, mungkin tidak ada, kerana ia sangat pelbagai. Masalah multiextremal amat sukar untuk diselesaikan.

Salah satu kaedah yang membolehkan anda mengurangkan masalah pengaturcaraan tak linear untuk menyelesaikan sistem persamaan ialah kaedah pengganda yang tidak ditentukan Lagrange.

Dengan menggunakan kaedah pengganda Lagrange, kami pada asasnya menubuhkan syarat yang diperlukan, membolehkan untuk mengenal pasti titik optimum dalam masalah pengoptimuman dengan kekangan dalam bentuk kesamaan. Dalam kes ini, masalah terkekang diubah menjadi masalah pengoptimuman tanpa syarat yang setara, yang melibatkan beberapa parameter yang tidak diketahui dipanggil pengganda Lagrange.

Kaedah pengganda Lagrange terdiri daripada mengurangkan masalah pada ekstrem bersyarat kepada masalah pada ekstrem tanpa syarat bagi fungsi tambahan - yang dipanggil. Fungsi Lagrange.

Untuk masalah ekstrem bagi sesuatu fungsi f(x 1, x 2,..., x n) di bawah keadaan (persamaan kekangan) φ i(x 1 , x 2 , ..., x n) = 0, i= 1, 2,..., m, fungsi Lagrange mempunyai bentuk

L(x 1, x 2… x n,λ 1, λ 2,…λm)=f(x 1, x 2… x n)+∑ i -1 m λ i φ i (x 1, x 2… x n)

Pengganda λ 1 , λ 2 , ..., λm dipanggil Pengganda Lagrange.

Jika nilai-nilai x 1 , x 2 , ..., x n , λ 1 , λ 2 , ..., λm intipati penyelesaian kepada persamaan yang menentukan titik pegun bagi fungsi Lagrange, iaitu, untuk fungsi boleh beza ialah penyelesaian kepada sistem persamaan

maka, di bawah andaian yang agak umum, x 1 , x 2 , ..., x n memberikan ekstrem bagi fungsi f.

Pertimbangkan masalah meminimumkan fungsi n pembolehubah tertakluk kepada satu kekangan dalam bentuk kesamaan:

Minimumkan f(x 1, x 2… x n) (1)

di bawah sekatan h 1 (x 1, x 2… x n)=0 (2)

Menurut kaedah pengganda Lagrange, masalah ini diubah menjadi masalah pengoptimuman tanpa kekangan berikut:

minimumkan L(x,λ)=f(x)-λ*h(x) (3)

di mana Fungsi L(x;λ) dipanggil fungsi Lagrange,

λ ialah pemalar yang tidak diketahui, yang dipanggil pengganda Lagrange. Tiada keperluan untuk tanda λ.

Biar pada tetapkan nilaiλ=λ 0 minimum tanpa syarat bagi fungsi L(x,λ) berkenaan dengan x dicapai pada titik x=x 0 dan x 0 memenuhi persamaan h 1 (x 0)=0. Kemudian, seperti yang mudah dilihat, x 0 meminimumkan (1) dengan mengambil kira (2), kerana untuk semua nilai x memuaskan (2), h 1 (x)=0 dan L(x,λ)=min f(x).

Sudah tentu, adalah perlu untuk memilih nilai λ=λ 0 supaya koordinat titik minimum tanpa syarat x 0 memenuhi kesamaan (2). Ini boleh dilakukan jika, mempertimbangkan λ sebagai pembolehubah, mencari minimum tanpa syarat fungsi (3) dalam bentuk fungsi λ, dan kemudian memilih nilai λ di mana kesamaan (2) dipenuhi. Mari kita gambarkan ini dengan contoh khusus.

Minimumkan f(x)=x 1 2 +x 2 2 =0

di bawah kekangan h 1 (x)=2x 1 +x 2 -2=0=0

Masalah pengoptimuman tanpa kekangan yang sepadan ditulis seperti berikut:

minimumkan L(x,λ)=x 1 2 +x 2 2 -λ(2x 1 +x 2 -2)

Penyelesaian. Menyamakan dua komponen kecerunan L kepada sifar, kita perolehi

→ x 1 0 =λ

→ x 2 0 =λ/2

Untuk menyemak sama ada titik pegun x° sepadan dengan minimum, kami mengira unsur-unsur matriks Hessian bagi fungsi L(x;u), dianggap sebagai fungsi x,

yang ternyata positif pasti.

Ini bermakna L(x,u) ialah fungsi cembung bagi x. Akibatnya, koordinat x 1 0 =λ, x 2 0 =λ/2 menentukan titik minimum global. Nilai optimumλ didapati dengan menggantikan nilai x 1 0 dan x 2 0 ke dalam persamaan 2x 1 + x 2 =2, dari mana 2λ+λ/2=2 atau λ 0 =4/5. Oleh itu, minimum bersyarat dicapai pada x 1 0 =4/5 dan x 2 0 =2/5 dan bersamaan dengan min f(x) = 4/5.

Apabila menyelesaikan masalah contoh, kami menganggap L(x;λ) sebagai fungsi dua pembolehubah x 1 dan x 2 dan, sebagai tambahan, mengandaikan bahawa nilai parameter λ telah dipilih supaya kekangan itu dipenuhi. Jika penyelesaian sistem

J=1,2,3,…,n

λ tidak boleh diperolehi dalam bentuk fungsi eksplisit, maka nilai x dan λ didapati dengan menyelesaikan sistem berikut yang terdiri daripada persamaan n+1 dengan n+1 tidak diketahui:

J=1,2,3,…,n., h 1 (x)=0

Untuk mencari semua orang penyelesaian yang mungkin Sistem ini boleh menggunakan kaedah carian berangka (contohnya, kaedah Newton). Bagi setiap penyelesaian (), kita harus mengira unsur-unsur matriks Hessian bagi fungsi L, dianggap sebagai fungsi x, dan mengetahui sama ada matriks ini pasti positif (minimum tempatan) atau pasti negatif (maksimum tempatan. ).

Kaedah pengganda Lagrange boleh diperluaskan kepada kes di mana masalah mempunyai beberapa kekangan dalam bentuk kesamaan. Pertimbangkan masalah umum yang memerlukan

Minimumkan f(x)

di bawah sekatan h k =0, k=1, 2, ..., K.

Fungsi Lagrange mengambil pandangan seterusnya:

Di sini λ 1 , λ 2 , ..., λk-Pengganda Lagrange, i.e. parameter yang tidak diketahui yang nilainya perlu ditentukan. Menyamakan terbitan separa L berkenaan dengan x kepada sifar, kita perolehi sistem berikut n persamaan dengan n tidak diketahui:

Jika ternyata sukar untuk mencari penyelesaian kepada sistem di atas dalam bentuk fungsi vektor λ, maka anda boleh mengembangkan sistem dengan memasukkan sekatan dalam bentuk persamaan

Penyelesaian sistem lanjutan, yang terdiri daripada persamaan n + K dengan n + K tidak diketahui, menentukan titik pegun fungsi L. Kemudian prosedur untuk menyemak minimum atau maksimum dilaksanakan, yang dijalankan berdasarkan pengiraan unsur-unsur matriks Hessian bagi fungsi L, dianggap sebagai fungsi x, sama seperti yang dilakukan dalam kes masalah dengan satu kekangan. Untuk beberapa masalah, sistem lanjutan persamaan n+K dengan n+K tidak diketahui mungkin tidak mempunyai penyelesaian, dan kaedah pengganda Lagrange ternyata tidak boleh digunakan. Walau bagaimanapun, perlu diingatkan bahawa tugas sedemikian agak jarang berlaku dalam amalan.

Mari kita pertimbangkan kes istimewa tugas biasa pengaturcaraan tak linear, dengan mengandaikan bahawa sistem kekangan hanya mengandungi persamaan, tiada syarat untuk bukan negatif pembolehubah dan dan - fungsi adalah berterusan bersama derivatif separanya. Oleh itu, dengan menyelesaikan sistem persamaan (7), kita memperoleh semua titik di mana fungsi (6) boleh mempunyai nilai ekstrem.

Algoritma untuk kaedah pengganda Lagrange

1. Karang fungsi Lagrange.

2. Cari terbitan separa bagi fungsi Lagrange berkenaan dengan pembolehubah x J ,λ i dan samakannya dengan sifar.

3. Kami menyelesaikan sistem persamaan (7), cari titik di mana fungsi objektif masalah boleh mempunyai ekstrem.

4. Antara mata yang mencurigakan untuk ekstrem, kita dapati titik di mana ekstrem dicapai, dan hitung nilai fungsi (6) pada titik ini.

Contoh.

Data awal: Mengikut rancangan pengeluaran, syarikat itu perlu mengeluarkan 180 produk. Produk ini boleh dihasilkan dalam dua cara teknologi. Apabila menghasilkan x 1 produk menggunakan kaedah pertama, kosnya ialah 4x 1 +x 1 2 rubel, dan apabila menghasilkan x 2 produk menggunakan kaedah ke-2, ia adalah 8x 2 +x 2 2 rubel. Tentukan berapa banyak produk yang perlu dikeluarkan menggunakan setiap kaedah supaya kos pengeluaran adalah minimum.

Fungsi objektif untuk masalah yang dinyatakan mempunyai bentuk
® min di bawah keadaan x 1 + x 2 =180, x 2 ≥0.
1. Karang fungsi Lagrange
.
2. Kami mengira terbitan separa berkenaan dengan x 1, x 2, λ dan menyamakannya dengan sifar:

3. Menyelesaikan sistem persamaan yang terhasil, kita dapati x 1 =91,x 2 =89

4. Setelah membuat penggantian dalam fungsi objektif x 2 =180-x 1, kita memperoleh fungsi satu pembolehubah, iaitu f 1 =4x 1 +x 1 2 +8(180-x 1)+(180-x 1 ) 2

Kami mengira atau 4x 1 -364=0 ,

dari mana kita mempunyai x 1 * =91, x 2 * =89.

Jawapan: Bilangan produk yang dihasilkan oleh kaedah pertama ialah x 1 =91, dengan kaedah kedua x 2 =89, manakala nilai fungsi objektif adalah bersamaan dengan 17,278 rubel.

• Tutorial

Semua orang hari yang baik. Dalam artikel ini saya ingin menunjukkan salah satu daripadanya kaedah grafik pembinaan model matematik untuk sistem dinamik, yang dipanggil graf bon("ikatan" - sambungan, "graf" - graf). Dalam kesusasteraan Rusia, saya mendapati penerangan kaedah ini hanya dalam Buku Teks Universiti Politeknik Tomsk, A.V. Voronin “MODELING OF MECHATRONIC SYSTEMS” 2008 Tunjukkan juga kaedah klasik melalui persamaan Lagrange jenis ke-2.

Kaedah Lagrange

Saya tidak akan menerangkan teori, saya akan menunjukkan peringkat pengiraan dengan beberapa ulasan. Secara peribadi, lebih mudah untuk saya belajar daripada contoh daripada membaca teori 10 kali. Nampaknya saya dalam kesusasteraan Rusia, penjelasan kaedah ini, dan sememangnya matematik atau fizik secara umum, sangat kaya. formula kompleks, yang sewajarnya memerlukan latar belakang matematik yang serius. Semasa mempelajari kaedah Lagrange (saya belajar di Universiti Politeknik Turin, Itali), saya mempelajari kesusasteraan Rusia untuk membandingkan kaedah pengiraan, dan sukar bagi saya untuk mengikuti kemajuan penyelesaian kaedah ini. Walaupun mengingati kursus pemodelan di Institut Penerbangan Kharkov, derivasi kaedah sedemikian sangat menyusahkan, dan tiada siapa yang mengganggu diri mereka dalam cuba memahami isu ini. Inilah yang saya putuskan untuk menulis, manual untuk membina model matematik mengikut Lagrange, kerana ternyata ia tidak sama sekali sukar, cukup untuk mengetahui cara mengira derivatif berkenaan dengan masa dan derivatif separa. Untuk model yang lebih kompleks, matriks putaran juga ditambah, tetapi tidak ada yang rumit di dalamnya.

Ciri kaedah pemodelan:

• Newton-Euler: persamaan vektor berdasarkan keseimbangan dinamik memaksa Dan detik-detik
• Lagrange: persamaan skalar berdasarkan fungsi keadaan yang dikaitkan dengan kinetik dan potensi tenaga
• Kiraan Bon: kaedah berasaskan aliran kuasa antara elemen sistem

Mari kita mulakan dengan contoh mudah. Jisim dengan spring dan peredam. Kami mengabaikan kuasa graviti.

Rajah 1. Jisim dengan spring dan peredam

Pertama sekali, kami menetapkan:

• sistem permulaan koordinat(NSK) atau sk tetap R0(i0,j0,k0). di mana? Anda boleh menuding jari anda ke langit, tetapi dengan menggerakkan hujung neuron di otak, idea itu berlalu untuk meletakkan NSC pada garis pergerakan badan M1.
• sistem koordinat bagi setiap jasad dengan jisim(kami ada M1 R1(i1,j1,k1)), orientasi boleh sewenang-wenangnya, tetapi mengapa merumitkan hidup anda, tetapkannya dengan perbezaan minimum daripada NSC
• koordinat umum q_i(bilangan minimum pembolehubah yang boleh menggambarkan pergerakan), dalam dalam contoh ini satu koordinat umum, pergerakan hanya sepanjang paksi j

Rajah 2. Kami meletakkan sistem koordinat dan koordinat umum

Rajah 3. Kedudukan dan kelajuan badan M1

Kemudian kita akan mencari tenaga kinetik (C) dan potensi (P) dan fungsi pelesapan (D) untuk peredam menggunakan formula:

Rajah 4. Formula lengkap tenaga kinetik

Dalam contoh kami tidak ada putaran, komponen kedua ialah 0.

Rajah 5. Pengiraan kinetik, tenaga keupayaan dan fungsi pelesapan

Persamaan Lagrange mempunyai bentuk berikut:

Rajah 6. Persamaan Lagrange dan Lagrangian

Delta W_i ini kerja maya disempurnakan oleh daya dan momen yang digunakan. Mari cari dia:

Rajah 7. Pengiraan kerja maya

di mana delta q_1 pergerakan maya.

Kami menggantikan semuanya ke dalam persamaan Lagrange:

Rajah 8. Model jisim yang terhasil dengan spring dan peredam

Di sinilah kaedah Lagrange berakhir. Seperti yang anda lihat, ia tidak begitu rumit, tetapi ia masih merupakan contoh yang sangat mudah, yang kemungkinan besar kaedah Newton-Euler akan menjadi lebih mudah. Untuk sistem yang lebih kompleks, di mana terdapat beberapa badan yang diputar secara relatif antara satu sama lain pada sudut yang berbeza, kaedah Lagrange akan menjadi lebih mudah.

Kaedah bon graf

Saya akan menunjukkan kepada anda dengan segera rupa model dalam graf ikatan sebagai contoh dengan jisim, spring dan peredam:

Rajah 9. Jisim graf ikatan dengan spring dan peredam

Di sini anda perlu memberitahu sedikit teori, yang cukup untuk dibina model ringkas. Jika ada yang berminat, boleh baca buku tersebut ( Graf Bon Metodologi) atau ( Voronin A.V. Pemodelan sistem mekatronik: tutorial. – Tomsk: Rumah Penerbitan Universiti Politeknik Tomsk, 2008).

Mari kita tentukan dahulu sistem yang kompleks terdiri daripada beberapa domain. Sebagai contoh, motor elektrik terdiri daripada bahagian atau domain elektrik dan mekanikal.

graf bon berdasarkan pertukaran kuasa antara domain ini, subsistem. Ambil perhatian bahawa pertukaran kuasa, dalam sebarang bentuk, sentiasa ditentukan oleh dua pembolehubah ( kuasa berubah-ubah) dengan bantuan yang mana kita boleh mengkaji interaksi pelbagai subsistem dalam sistem dinamik (lihat jadual).

Seperti yang dapat dilihat dari jadual, ekspresi kuasa hampir sama di mana-mana. Secara ringkasnya, Kuasa- Kerja ini " aliran - f"pada" usaha - e».

Usaha(Bahasa Inggeris) usaha) dalam domain elektrik ini adalah voltan (e), dalam domain mekanikal ia adalah daya (F) atau tork (T), dalam hidraulik ia adalah tekanan (p).

Aliran(Bahasa Inggeris) aliran) dalam domain elektrik ia adalah arus (i), dalam domain mekanikal ia adalah kelajuan (v) atau halaju sudut (omega), dalam hidraulik ia adalah aliran atau kadar aliran bendalir (Q).

Mengambil notasi ini, kami memperoleh ungkapan untuk kuasa:

Rajah 10. Formula kuasa melalui pembolehubah kuasa

Dalam bahasa graf ikatan, hubungan antara dua subsistem yang bertukar kuasa diwakili oleh ikatan. ikatan). Itulah sebabnya kaedah ini dipanggil graf ikatan atau g raf-sambungan, graf bersambung. Mari kita pertimbangkan gambarajah blok sambungan dalam model dengan motor elektrik (ini bukan graf ikatan lagi):

Rajah 11. Gambar rajah blok aliran kuasa antara domain

Jika kita mempunyai sumber voltan, maka dengan itu ia menghasilkan voltan dan memindahkannya ke motor untuk penggulungan (inilah sebabnya anak panah diarahkan ke motor), bergantung pada rintangan belitan, arus muncul mengikut undang-undang Ohm (diarahkan dari motor ke sumber). Oleh itu, satu pembolehubah adalah input kepada subsistem, dan yang kedua mestilah keluar daripada subsistem. Di sini voltan ( usaha) – input, semasa ( aliran) - keluar.

Jika anda menggunakan sumber semasa, bagaimanakah rajah akan berubah? Betul. Arus akan diarahkan ke motor, dan voltan ke punca. Kemudian arus ( aliran) – input, voltan ( usaha) - keluar.

Mari kita lihat contoh dalam mekanik. Daya bertindak ke atas jisim.

Rajah 12. Daya dikenakan pada jisim

Rajah blok adalah seperti berikut:

Rajah 13. Gambarajah blok

Dalam contoh ini, Kekuatan ( usaha) – pembolehubah input untuk jisim. (Daya dikenakan pada jisim)
Menurut hukum kedua Newton:

Jisim bertindak balas dengan kelajuan:

Dalam contoh ini, jika satu pembolehubah ( memaksa - usaha) ialah pintu masuk ke dalam domain mekanikal, kemudian pembolehubah kuasa lain ( kelajuan - aliran) – secara automatik menjadi keluar.

Untuk membezakan di mana input dan di mana output, ia digunakan garis menegak pada penghujung anak panah (sambungan) antara elemen, baris ini dipanggil tanda kausalitas atau sebab musabab (sebab musabab). Ternyata: daya yang dikenakan adalah punca, dan kelajuan adalah kesannya. Tanda ini sangat penting untuk pembinaan model sistem yang betul, kerana kausaliti adalah akibat daripada tingkah laku fizikal dan pertukaran kuasa dua subsistem, oleh itu pilihan lokasi tanda kausaliti tidak boleh sewenang-wenangnya.

Rajah 14. Penetapan sebab akibat

Garis menegak ini menunjukkan subsistem yang menerima daya ( usaha) dan akibatnya menghasilkan aliran ( aliran). Dalam contoh dengan jisim ia akan menjadi seperti ini:

Rajah 14. Hubungan sebab bagi daya yang bertindak ke atas jisim

Jelas daripada anak panah bahawa input untuk jisim ialah - memaksa, dan outputnya ialah kelajuan. Ini dilakukan supaya tidak mengacaukan rajah dengan anak panah dan mensistematikkan pembinaan model.

Seterusnya perkara penting. Dorongan umum(jumlah pergerakan) dan bergerak(pembolehubah tenaga).

Jadual pembolehubah kuasa dan tenaga dalam domain yang berbeza

Jadual di atas memperkenalkan dua kuantiti fizik tambahan yang digunakan dalam kaedah graf ikatan. Mereka dipanggil impuls umum (R) Dan pergerakan umum (q) atau pembolehubah tenaga, dan ia boleh diperoleh dengan menyepadukan pembolehubah kuasa dari semasa ke semasa:

Rajah 15. Hubungan antara pembolehubah kuasa dan tenaga

Dalam domain elektrik :

Berdasarkan hukum Faraday, voltan di hujung konduktor adalah sama dengan terbitan fluks magnet melalui konduktor ini.

A Kekuatan semasa - kuantiti fizikal, sama dengan nisbah jumlah cas Q yang melalui keratan rentas konduktor dalam beberapa masa t kepada nilai selang masa ini.

Domain mekanikal:

Daripada hukum ke-2 Newton, Paksa– terbitan masa bagi impuls

Dan selaras dengan itu, kelajuan- terbitan masa bagi sesaran:

Mari kita ringkaskan:

Elemen asas

Semua elemen dalam sistem dinamik, boleh dibahagikan kepada komponen dua kutub dan empat kutub.
Mari kita pertimbangkan komponen bipolar:

Sumber
Terdapat sumber kedua-dua usaha dan aliran. Analogi dalam domain elektrik: sumber usaha – punca voltan, sumber aliran – sumber semasa. Tanda-tanda sebab untuk sumber hanya sepatutnya seperti ini.

Rajah 16. Sambungan sebab dan penetapan sumber

Komponen R - unsur pelesapan

Komponen I - unsur inersia

Komponen C – unsur kapasitif

Seperti yang dapat dilihat daripada rajah, elemen yang berbeza satu jenis R,C,I diterangkan oleh persamaan yang sama. HANYA terdapat perbezaan untuk kapasiti elektrik, anda hanya perlu mengingatinya!

Komponen quadrupole:

Mari kita lihat dua komponen: pengubah dan girator.

Terakhir komponen penting Dalam kaedah graf bon, sambungan digunakan. Terdapat dua jenis nod:

Itu sahaja dengan komponen.

Langkah-langkah utama untuk mewujudkan hubungan sebab akibat selepas membina graf ikatan:

1. Berikan hubungan sebab akibat kepada semua orang sumber
2. Pergi melalui semua nod dan letakkan hubungan sebab akibat selepas titik 1
3. Untuk komponen I tetapkan hubungan sebab input (usaha disertakan dalam komponen ini), untuk komponen C tetapkan kausalitas output (usaha keluar dari komponen ini)
4. Ulang titik 2
5. Sisipkan sambungan sebab untuk komponen R

Ini menyimpulkan kursus mini tentang teori. Kini kami mempunyai semua yang kami perlukan untuk membina model.
Mari kita selesaikan beberapa contoh. Mari kita mulakan dengan litar elektrik, adalah lebih baik untuk memahami analogi membina graf ikatan.

Contoh 1

Mari mulakan membina graf ikatan dengan sumber voltan. Hanya tulis Se dan letakkan anak panah.

Lihat, semuanya mudah! Mari kita lihat lebih jauh, R dan L disambungkan secara bersiri, yang bermaksud arus yang sama mengalir di dalamnya, jika kita bercakap dalam pembolehubah kuasa - aliran yang sama. Nod yang manakah mempunyai aliran yang sama? Jawapan yang betul ialah 1-nod. Kami menyambungkan sumber, rintangan (komponen - R) dan kearuhan (komponen - I) ke 1-nod.

Seterusnya, kami mempunyai kapasitans dan rintangan secara selari, yang bermaksud mereka mempunyai voltan atau daya yang sama. 0-nod adalah sesuai seperti yang lain. Kami menyambungkan kapasitansi (komponen C) dan rintangan (komponen R) ke 0-nod.

Kami juga menyambungkan nod 1 dan 0 antara satu sama lain. Arah anak panah dipilih sewenang-wenangnya; arah sambungan hanya mempengaruhi tanda dalam persamaan.

Anda akan mendapat graf sambungan berikut:

Sekarang kita perlu mewujudkan hubungan sebab akibat. Mengikuti arahan untuk urutan penempatan mereka, mari kita mulakan dengan sumber.

1. Kami mempunyai sumber voltan (usaha), sumber sedemikian hanya mempunyai satu pilihan kausaliti - output. Jom pakai.
2. Seterusnya terdapat komponen I, mari lihat apa yang mereka cadangkan. Kita letak
3. Kami meletakkannya untuk 1-nod. makan
4. Nod 0 mesti mempunyai satu input dan semua sambungan sebab keluaran. Kami mempunyai satu hari cuti buat masa ini. Kami sedang mencari komponen C atau I. Kami menjumpainya. Kita letak
5. Mari senaraikan apa yang tinggal

Itu sahaja. Graf bon dibina. Hore, Kawan-kawan!

Yang tinggal hanyalah menulis persamaan yang menerangkan sistem kami. Untuk melakukan ini, buat jadual dengan 3 lajur. Yang pertama akan mengandungi semua komponen sistem, yang kedua akan mengandungi pembolehubah input untuk setiap elemen, dan yang ketiga akan mengandungi pembolehubah output untuk komponen yang sama. Kami telah pun mentakrifkan input dan output mengikut hubungan sebab akibat. Jadi tidak sepatutnya ada masalah.

Mari kita nombor setiap sambungan untuk memudahkan merekod tahap. Kami mengambil persamaan untuk setiap elemen dari senarai komponen C, R, I.

Setelah menyusun jadual, kami menentukan pembolehubah keadaan, dalam contoh ini terdapat 2 daripadanya, p3 dan q5. Seterusnya anda perlu menulis persamaan keadaan:

Itu sahaja, model sudah siap.

Contoh 2. Saya ingin segera memohon maaf atas kualiti foto, perkara utama ialah anda boleh membaca

Mari kita selesaikan contoh lain untuk sistem mekanikal, yang sama yang kami selesaikan menggunakan kaedah Lagrange. Saya akan tunjukkan penyelesaiannya tanpa komen. Mari kita semak kaedah mana yang lebih mudah dan mudah.

Di Matbala, kedua-dua model matematik dengan parameter yang sama telah disusun, diperoleh dengan kaedah Lagrange dan graf ikatan. Hasilnya adalah di bawah: Tambah tag