Hari ini kita akan melihat lebih dekat pada peranti itu kamera maya. Mari kita mulakan dengan gambar.
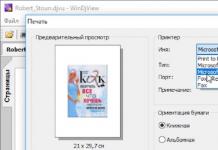
Dalam rajah kita melihat ruang koordinat kamera. Arah ("pandangan") kamera sentiasa bertepatan dengan arah positif paksi z, dan kamera itu sendiri terletak di tempat asal.
Ruang dalaman piramid yang ditunjukkan dalam rajah ialah bahagian dunia maya yang akan dilihat oleh pengguna.
Perhatikan tiga pesawat. Yang pertama terletak pada jarak 1 di sepanjang paksi z. Ini adalah kapal terbang yang berhampiran. Pemain tidak akan melihat apa yang sebelum ini. DALAM dalam kes ini nilai z adalah sama dengan satu, tetapi secara amnya ia boleh menjadi apa sahaja. Satu kecacatan paparan grafik dikaitkan dengan satah berhampiran. Kecacatan ini nyata terutamanya dalam penembak (disebabkan oleh kebebasan besar kamera). Apabila anda terlalu dekat dengan objek, anda boleh berada di "dalam". daripada permainan terkini Kecacatan ini amat ketara dalam Kiri 4 mati: apabila sekumpulan zombi jatuh ke atas pemain, selalunya mungkin untuk melihat ke dalam watak lain.
Satah yang terletak pada jarak 100 unit di sepanjang paksi z dipanggil satah jauh. Sekali lagi, nilainya boleh sewenang-wenangnya. Pengguna tidak akan melihat objek yang terletak lebih jauh daripada pesawat ini.
Enam satah yang mengehadkan ruang yang akan dilihat pengguna dipanggil satah keratan: kiri, kanan, atas, bawah, dekat dan jauh.
Pesawat yang terletak di antara jarak dekat dan jauh adalah unjuran. Dalam perkara berikut, kita akan meletakkan satah ini pada z=1, i.e. ia akan bertepatan dengan yang terdekat. Di sini saya memisahkan pesawat dekat dan unjuran untuk menunjukkan bahawa mereka bukan perkara yang sama. Satah unjuran bertujuan untuk transformasi koordinat akhir: transformasi daripada ruang kamera tiga dimensi kepada ruang dua dimensi.
Ia adalah terima kasih kepada satah unjuran yang pengguna akan lihat alam maya. Sebenarnya, pesawat ini adalah apa yang pengguna akan lihat. Satah unjuran berkaitan secara langsung dengan konsep seperti penampan latar depan/latar belakang, tetingkap program dan skrin pengguna. Semua konsep ini boleh dianggap sebagai gambar segi empat tepat, yang diwakili dalam memori komputer dengan pelbagai nombor.
Menukar koordinat daripada dunia tiga dimensi kepada satah unjuran adalah yang paling sukar daripada yang ada masa ini telah dipelajari oleh kami.
Medan pandangan
Dalam rajah di atas, satah unjuran (dan oleh itu imej yang akan dilihat pengguna) mempunyai lebar yang lebih besar daripada ketinggiannya. Lebar dan tinggi satah unjuran ditentukan menggunakan sudut. jumpa nama yang berbeza sudut ini: medan pandangan atau kawasan tontonan. Dalam bahasa Inggeris - bidang pandangan. 
Kawasan tontonan ditentukan oleh dua sudut. Mari kita panggil mereka: fovx - kawasan tontonan mendatar, fovy - kawasan tontonan menegak. Butiran tentang kawasan tontonan: di bawah.
Z-buffer / w-buffer / depth buffer (z-buffer / w-buffer / depth buffer)
Mari lihat gambar, yang menunjukkan dua segi tiga: pada jarak 25 dan 50 unit dari kamera. Rajah (a) menunjukkan lokasi segi tiga dalam ruang (pandangan atas), dan rajah (b) menunjukkan imej akhir: 
Seperti yang anda fikirkan, imej perlu dilukis bermula dari elemen yang paling jauh dan berakhir dengan yang paling dekat. Penyelesaian yang jelas: Kira jarak dari asal (dari kamera) ke setiap objek dan kemudian bandingkan. DALAM grafik komputer mekanisme yang lebih maju sedikit digunakan. Mekanisme ini mempunyai beberapa nama: z-buffer, w-buffer, depth buffer. Saiz penimbal-z dari segi bilangan elemen adalah sama dengan saiz latar belakang dan penimbal utama. Komponen z bagi objek yang paling hampir dengan kamera dimasukkan ke dalam penimbal z. DALAM dalam contoh ini, di mana segitiga biru bertindih dengan yang hijau, koordinat z bagi yang biru akan dimasukkan ke dalam penimbal kedalaman. Kita akan bercakap tentang penimbal-z dengan lebih terperinci dalam pelajaran yang berasingan.
Unjuran ortografik / selari
Operasi di mana dimensi ruang berkurangan (terdapat ruang tiga dimensi, ia menjadi dua dimensi) dipanggil unjuran. Pertama sekali, kita berminat dengan unjuran perspektif, tetapi mula-mula kita akan berkenalan dengan selari (unjuran selari atau ortografik). 
Untuk mengira unjuran selari, cukup untuk membuang koordinat tambahan. Jika kita mempunyai titik dalam ruang [ 3 3 3 ], maka dengan unjuran selari pada satah z=1, ia akan diunjurkan ke dalam titik .
Unjuran perspektif pada satah unjuran
Dalam jenis unjuran ini, semua garisan menumpu pada satu titik. Beginilah cara penglihatan kita berfungsi. Dan ia adalah dengan bantuan unjuran perspektif bahawa "rupa" dalam semua permainan dimodelkan.

Bandingkan gambar ini dengan gambar yang menunjukkan koordinat homogen dari pelajaran sebelumnya. Untuk bergerak dari ruang tiga dimensi ke ruang dua dimensi, anda perlu membahagikan dua komponen pertama vektor dengan yang ketiga: [ x/z y/z z/z ] = [ x/z y/z 1 ].
Seperti yang saya tulis di atas, satah unjuran boleh terletak di mana-mana antara dekat dan jauh. Kami akan sentiasa meletakkan satah unjuran pada z=1, tetapi dalam tutorial ini kami akan melihat pilihan lain. Jom tengok gambar:

Mari kita nyatakan jarak ke satah unjuran dari asal koordinat sebagai d. Kami akan mempertimbangkan dua kes: d=1 dan d=5. Perkara penting: komponen ketiga semua vektor selepas unjuran mestilah sama dengan d - semua titik terletak dalam satah yang sama z=d. Ini boleh dicapai dengan mendarab semua komponen vektor dengan d: [ xd/z yd/z zd/z ]. Dengan d=1, kita dapat: [ x/z y/z 1 ], ini ialah formula yang digunakan untuk mengubah koordinat homogen.
Sekarang, jika kita menggerakkan satah unjuran ke titik z=5 (masing-masing d=5), kita dapat: [ xd/z yd/z zd/z ] = [ 5x/z 5y/z 5 ]. Formula terakhir memproyeksikan semua vektor ruang ke dalam satu satah, dengan d=5.
Kami mempunyai sedikit masalah di sini. Formula sebelumnya berfungsi dengan vektor tiga dimensi. Tetapi kami bersetuju untuk menggunakan vektor empat dimensi. Komponen keempat dalam kes ini hanya boleh dibuang. Tetapi kami tidak akan melakukan ini, kerana penggunaannya menyediakan beberapa keupayaan khusus yang akan kami bincangkan kemudian.
Anda perlu mencari pembahagi sepunya bagi komponen ketiga dan keempat, apabila dibahagikan dengan mana nilai d kekal dalam komponen ketiga, dan perpaduan dalam komponen keempat. Pembahagi ini ialah d/z. Sekarang daripada vektor biasa [ x y z 1 ] kita perlu menyediakan vektor sedia untuk unjuran (bahagian) [ x y z z/d ]. Ini dilakukan menggunakan matriks transformasi (semak hasilnya dengan mendarab mana-mana vektor dengan matriks ini):

Transformasi terakhir belum lagi unjuran. Di sini kita hanya mengurangkan semua vektor kepada bentuk yang kita perlukan. Biar saya ingatkan anda bahawa kami akan meletakkan satah unjuran pada d=1, yang bermaksud vektor akan kelihatan seperti ini: [ x y z z ].
Matriks transformasi yang menjanjikan
Kami akan melihat matriks transformasi perspektif yang digunakan dalam DirectX: 
Sekarang kita tahu elemen _34 dimaksudkan untuk apa. Kami juga tahu bahawa elemen _11 dan _22 menskalakan imej secara mendatar dan menegak. Mari kita lihat apa sebenarnya yang tersembunyi di sebalik nama xScale dan yScale.
Pembolehubah ini bergantung pada kawasan tontonan yang kami bincangkan di atas. Dengan menambah atau mengurangkan sudut ini, anda boleh skala (skala atau zum) imej - menukar saiz dan nisbah bidang satah unjuran. Mekanisme zum samar-samar mengingatkan zum dalam kamera/kamera - prinsipnya sangat serupa. Jom tengok gambar:

Mari bahagikan sudut fov kepada dua bahagian dan pertimbangkan hanya separuh. Apa yang kita lihat di sini: dengan meningkatkan sudut fov/2 (dan, sewajarnya, sudut fov), kita meningkatkan dosa sudut dan mengurangkan cos. Ini membawa kepada peningkatan dalam satah unjuran dan, dengan itu, kepada penurunan dalam objek yang diunjurkan. Sudut yang sesuai untuk kita ialah fov/2 = P/4. Biar saya ingatkan anda bahawa sudut dalam P/4 radian adalah bersamaan dengan 45 darjah. Dalam kes ini, fov akan sama dengan 90 darjah. Mengapa sudut 45 darjah baik untuk kita? Dalam kes ini, tiada penskalaan, dan cos(P/4)/sin(P/4)=1.
Sekarang kita boleh dengan mudah menskalakan imej secara menegak (mendatar) menggunakan sinus dan kosinus separuh kawasan tontonan (fungsi kotangen dalam C++ dipanggil cot):
Skala y = cos(fovY/2)/sin(fovY/2) = cot(fovY/2)
DirectX hanya menggunakan FOV menegak (fovY), dan penskalaan mendatar bergantung pada FOV menegak dan nisbah bidang.
Biar saya ingatkan anda bahawa tetingkap dalam program kami bersaiz 500x500. Nisbah aspek: 1 hingga 1. Oleh itu, pembolehubah akan sama: xSkala=1, ySkala=1.
Nisbah bidang monitor/TV standard: 4:3. Nisbah ini sepadan dengan resolusi skrin: 640x480, 800x600, 1600x1200. Kami tidak akan menyentuh lagi mod skrin penuh, tetapi kita boleh menukar saiz tetingkap program. Anda boleh menukar saiz tetingkap (dalam parameter sekarang), sebagai contoh, kepada 640X480. Tetapi untuk mengelakkan semua objek daripada diregangkan (petak akan kelihatan seperti segi empat tepat), jangan lupa untuk menukar pembolehubah yang sepadan dalam matriks unjuran.
Saya hampir terlupa, forum untuk xScale dalam DirectX:
xSkala = ySkala / nisbah bidang
Nisbah aspek ditetapkan secara ringkas: 1/1, 4/3, 16/9 - ini adalah yang standard.
Ia kekal untuk mengetahui tujuan unsur _33, _34 matriks transformasi perspektif. zf ialah koordinat z bagi satah jauh (dari jauh - jauh), dan zn ialah koordinat z bagi satah dekat (dari dekat - dekat). Ambil perhatian bahawa unsur _43 = _33 * -zn.
Cara paling mudah untuk memahami dengan tepat apa yang formula ini lakukan adalah dengan contoh. Mari kita darabkan vektor piawai [ x y z w ] dengan matriks yang dibentangkan di atas. Saya mengesyorkan agar anda melakukan ini dengan mengambil sekeping kertas dan pensel (saya harap anda ingat bagaimana untuk mendarab dua matriks). Komponen vektor akan mengambil bentuk berikut.
1 = x*xSkala
ke-2 = Skala y*y
ke-3 = z*(zf/(zf-zn)) + w*(-(zn*zf)/(zf-zn)) = (zf/(zf-zn))*(z - w*zn)
Ke-4 = (w*z)/h
Mari lakukan transformasi unjuran (kita bahagikan semua elemen kepada komponen ke-4, dan anggap bahawa d=1 dan w=1):
Pertama = (d*x*xSkala)/(w*z) = (x*xScale)/z
Ke-2 = (d*y*ySkala)/(w*z) = (y*xScale)/z
Ke-3 = (zf/(zf-zn))*(z - w*zn)*(w*d/z) = (zf/(zf-zn))*(1 - zn/z)
ke-4 = 1
Akibatnya, kami menerima vektor borang:
[ x/(z*xScale) y/(z*yScale) (zf/(zf-zn))*(1-zn/z) 1 ]
Sekarang, jika anda menentukan nilai khusus untuk zf dan zn, anda akan mendapati perkara berikut (untuk nilai positif): jika vektor terletak sebelum satah berhampiran, maka komponen z selepas transformasi akan menjadi kurang daripada sifar, jika vektor terletak di belakang satah jauh, maka komponen z akan menjadi unit yang lebih besar.
Tiada perbezaan di mana tepatnya satah dekat dan jauh terletak: zn=1, zf=10 atau zn=10, dan zf=100 (atau mana-mana nilai lain) - selepas penjelmaan, kawasan yang boleh dilihat akan terletak dalam selang dari sifar kepada satu, termasuk.
Inilah yang dimaksudkan dengan formula dalam elemen _33, _34 matriks unjuran - untuk mengunjurkan jarak dari satah dekat ke jauh ke dalam segmen. Semak ini dengan mengira nilai beberapa vektor untuk nilai khusus zn,zf (ya, pada sehelai kertas!!!).
DALAM detik tertentu Mana-mana pembangun dalam bidang grafik komputer mempunyai soalan: bagaimanakah matriks yang menjanjikan ini berfungsi? Kadangkala jawapannya sangat sukar dicari dan, seperti yang biasa berlaku, majoriti pembangun menyerah pada separuh jalan menjalankan tugas.
Ini bukan penyelesaian kepada masalah! Mari kita fikirkan bersama!
Mari menjadi realistik dengan berat sebelah praktikal dan ambil sebagai subjek ujian Versi OpenGL 3.3. Bermula daripada versi ini, setiap pembangun dikehendaki melaksanakan modul secara bebas operasi matriks. Hebat, ini yang kita perlukan. Marilah kita menguraikan tugas sukar kita dan menyerlahkan perkara utama. Beberapa fakta daripada spesifikasi OpenGL:
- Matriks disimpan dalam lajur (lajur-utama);
- Koordinat homogen;
- Isipadu kliping kanonik (CVV) dalam sistem koordinat kidal.
Koordinat homogen bukanlah sistem yang sangat rumit dengan beberapa peraturan mudah untuk menukar koordinat Cartesan konvensional kepada koordinat homogen dan sebaliknya. Koordinat homogen ialah matriks baris dimensi . Untuk menukar koordinat Cartesan kepada koordinat homogen, adalah perlu x, y Dan z darab dengan sebarang nombor nyata w(kecuali 0). Seterusnya, anda perlu menulis keputusan dalam tiga komponen pertama, dan komponen terakhir akan sama dengan pengganda w. Dalam kata lain:
- Koordinat Cartesan
w– nombor nyata tidak sama dengan 0 - koordinat homogen
Sedikit helah: Jika w sama dengan satu, maka semua yang diperlukan untuk terjemahan ialah memindahkan komponen x, y Dan z dan tetapkan satu kepada komponen terakhir. Iaitu, dapatkan matriks baris:
Beberapa perkataan tentang kualiti sifar w. Dari sudut pandangan koordinat homogen, ini agak boleh diterima. Koordinat homogen membolehkan anda membezakan antara titik dan vektor. Dalam sistem koordinat Cartesian, pembahagian sedemikian adalah mustahil. - titik di mana ( x, y, z) – Koordinat Cartesan
- vektor, di mana ( x, y, z) – vektor jejari
Terjemahan songsang sesuatu bucu daripada koordinat homogen kepada koordinat Cartesan dilakukan seperti berikut. Semua komponen matriks baris mesti dibahagikan dengan komponen terakhir. Dalam kata lain: - koordinat homogen
- Koordinat Cartesan
Perkara utama yang perlu anda ketahui ialah semua algoritma pemotongan dan rasterisasi OpenGL berfungsi dalam koordinat Cartesian, tetapi sebelum itu semua transformasi dilakukan dalam koordinat homogen. Peralihan daripada koordinat homogen ke koordinat Cartesian dijalankan dalam perkakasan.
Jumlah keratan kanonik (CVV) ialah salah satu bahagian OpenGL yang paling kurang didokumentasikan. Seperti yang dapat dilihat dari Rajah. 1 CVV ialah kubus sejajar paksi berpusat pada asalan dan dengan panjang tepi bersamaan dengan dua. Semua yang berada dalam kawasan CVV tertakluk kepada rasterisasi, semua yang berada di luar CVV diabaikan. Apa-apa sahaja yang sebahagiannya berada di luar CVV tertakluk kepada algoritma pemangkasan. Perkara paling penting yang perlu anda ketahui ialah sistem koordinat CVV adalah kidal!
nasi. 1. Jumlah keratan OpenGL Canonical (CVV)
Sistem koordinat kidal? Bagaimanakah ini boleh berlaku, kerana spesifikasi untuk OpenGL 1.0 dengan jelas menyatakan bahawa sistem koordinat yang digunakan adalah tangan kanan? Mari kita fikirkan.
nasi. 2. Sistem koordinat
Seperti yang dapat dilihat dari Rajah. 2 sistem koordinat berbeza hanya dalam arah paksi Z. OpenGL 1.0 sebenarnya menggunakan tangan kanan sistem pengguna koordinat Tetapi sistem koordinat CVV dan sistem koordinat pengguna adalah dua perkara yang sama sekali berbeza. Lebih-lebih lagi, pada versi 3.3, tidak ada lagi perkara seperti itu sistem piawai Koordinat OpenGL. Seperti yang dinyatakan sebelum ini, pengaturcara sendiri melaksanakan modul operasi matriks. Pembentukan matriks putaran, pembentukan matriks unjuran, cari matriks songsang, pendaraban matriks - ini ialah set operasi minimum yang disertakan dalam modul operasi matriks. Dua soalan logik timbul. Jika kelantangan keterlihatan ialah kubus dengan panjang tepi bersamaan dengan dua, maka mengapa pemandangan bersaiz beberapa ribu kelihatan pada skrin? Pada titik manakah sistem koordinat pengguna bertukar kepada sistem koordinat CVV? Matriks unjuran ialah entiti yang berurusan dengan isu ini.
Idea utama di atas ialah pembangun sendiri bebas memilih jenis sistem koordinat pengguna dan mesti menerangkan dengan betul matriks unjuran. Itu sahaja dengan fakta tentang OpenGL dan sudah tiba masanya untuk menyatukan segala-galanya.
Salah satu matriks yang paling biasa dan sukar untuk difahami ialah matriks transformasi perspektif. Jadi bagaimana ia berkaitan dengan CVV dan sistem koordinat pengguna? Mengapakah objek menjadi lebih kecil apabila jaraknya dari pemerhati bertambah? Untuk memahami sebab objek menjadi lebih kecil apabila jarak bertambah, mari kita lihat transformasi matriks model tiga dimensi langkah demi langkah. Bukan rahsia lagi bahawa mana-mana model tiga dimensi terdiri daripada senarai terhingga bucu yang menjalani transformasi matriks secara bebas antara satu sama lain. Untuk menentukan koordinat bucu tiga dimensi pada skrin monitor dua dimensi, anda perlu:
- Tukar koordinat Cartesan kepada koordinat homogen;
- Darabkan koordinat homogen dengan matriks model;
- Hasilnya didarab dengan matriks pandangan;
- Darabkan hasil dengan matriks unjuran;
- Tukarkan hasil daripada koordinat homogen kepada koordinat Cartesan.
Sekarang mari kita pergi ke langkah tiga. Di sinilah ruang pandangan berperanan. Dalam ruang ini, koordinat diukur secara relatif kepada kedudukan dan orientasi pemerhati seolah-olah dia adalah pusat dunia. Ruang paparan adalah relatif setempat kepada ruang dunia, jadi koordinat mesti dimasukkan ke dalamnya (dan tidak dikeluarkan, seperti dalam kes sebelumnya). Penjelmaan matriks langsung mengalih keluar koordinat dari beberapa ruang. Dalam usaha, sebaliknya, untuk memperkenalkan mereka ke dalamnya, adalah perlu untuk menyongsangkan transformasi matriks, oleh itu transformasi jenis diterangkan oleh matriks songsang. Bagaimana untuk mendapatkan ini matriks songsang? Mula-mula, mari dapatkan matriks pemerhati langsung. Apakah ciri seorang pemerhati? Pemerhati diterangkan oleh koordinat di mana dia berada dan vektor arah tontonan. Pemerhati sentiasa melihat ke arah paksi tempatannya Z. Pemerhati boleh bergerak di sekitar tempat kejadian dan membuat giliran. Dalam banyak cara, ini menyerupai makna matriks model. Secara umumnya, beginilah keadaannya. Walau bagaimanapun, bagi pemerhati, operasi penskalaan tidak bermakna, oleh itu, tanda sama tidak boleh diletakkan di antara matriks model pemerhati dan matriks model objek tiga dimensi. Matriks model pemerhati ialah matriks langsung yang dikehendaki. Dengan menyongsangkan matriks ini, kita memperoleh matriks pandangan. Dalam amalan, ini bermakna semua bucu dalam koordinat homogen global akan menerima koordinat homogen baharu berbanding pemerhati. Sehubungan itu, jika pemerhati melihat bucu tertentu, maka nilai koordinat homogen z daripada bucu yang diberikan dalam ruang pandangan pasti akan ada nombor positif. Jika bucu berada di belakang pemerhati, maka nilai koordinat homogennya z dalam ruang pandangan pasti akan menjadi nombor negatif.
Langkah keempat adalah langkah yang paling menarik. Langkah-langkah sebelumnya telah dibincangkan dengan terperinci sedemikian dengan sengaja supaya pembaca mempunyai gambaran lengkap tentang semua operan langkah keempat. Pada langkah keempat, koordinat homogen dipindahkan dari ruang pandangan ke ruang CVV. Sekali lagi, fakta ditegaskan bahawa semua bucu yang berpotensi kelihatan akan mempunyai nilai positif koordinat homogen. z.
Pertimbangkan matriks bentuk:
Dan satu titik dalam ruang homogen pemerhati:
Mari kita darabkan koordinat homogen dengan matriks yang dipersoalkan:
Mari tukarkan koordinat homogen yang terhasil kepada koordinat Cartesan:
Katakan terdapat dua titik dalam ruang paparan dengan koordinat yang sama x Dan y, tetapi dengan koordinat yang berbeza z. Dalam erti kata lain, salah satu mata berada di belakang yang lain. Oleh kerana herotan perspektif, pemerhati mesti melihat kedua-dua mata. Sememangnya jelas dari formula bahawa disebabkan pembahagian oleh koordinat z, mampatan berlaku ke titik asal. Semakin tinggi nilainya z(semakin jauh titik dari pemerhati), itu mampatan yang lebih kuat. Ini adalah penjelasan untuk kesan perspektif.
Spesifikasi OpenGL menyatakan bahawa operasi keratan dan rasterisasi dilakukan dalam koordinat Cartesan, dan proses menukar koordinat homogen kepada koordinat Cartesan dilakukan secara automatik.
Matriks (1) ialah templat untuk matriks unjuran perspektif. Seperti yang dinyatakan sebelum ini, tugas matriks unjuran terdiri daripada dua perkara: menetapkan sistem koordinat pengguna (kidal atau kanan), memindahkan volum keterlihatan pemerhati ke CVV. Mari terbitkan matriks perspektif untuk sistem koordinat pengguna kidal.
Matriks unjuran boleh diterangkan dengan dengan bantuan empat orang parameter (Gamb. 3):
- Sudut pandangan dalam radian ( fovy);
- Nisbah aspek ( aspek);
- Jarak ke satah keratan terdekat ( n);
- Jarak ke satah keratan jauh ( f).
nasi. 3. Jumlah keterlihatan perspektif
Mari kita pertimbangkan unjuran titik dalam ruang pemerhati ke tepi hadapan potongan isipadu keterlihatan perspektif. Untuk lebih jelas, dalam Rajah. 4 menunjukkan pandangan sisi. Ia juga perlu diambil kira bahawa sistem koordinat pengguna bertepatan dengan sistem koordinat CVV, iaitu sistem koordinat kidal digunakan di mana-mana.
nasi. 4. Mengunjurkan titik sewenang-wenangnya
Berdasarkan sifat segi tiga yang serupa, persamaan berikut adalah benar:
Mari kita ungkapkan y7 dan x7:
Pada dasarnya, ungkapan (2) adalah mencukupi untuk mendapatkan koordinat titik unjuran. Walau bagaimanapun, untuk menyaring objek tiga dimensi dengan betul, anda perlu mengetahui kedalaman setiap serpihan. Dalam erti kata lain, adalah perlu untuk menyimpan nilai komponen z. Ini ialah nilai yang digunakan untuk ujian kedalaman OpenGL. Dalam Rajah. 3 adalah jelas bahawa nilai z7 tidak sesuai sebagai kedalaman serpihan, kerana semua unjuran titik boleh nilai yang sama z7. Jalan keluar dari situasi ini adalah dengan menggunakan pseudo-depth yang dipanggil.
Sifat kedalaman pseudo:
- Kedalaman pseudo dikira berdasarkan nilai z;
- Semakin dekat titik dengan pemerhati, semakin kurang nilai pseudodepth;
- Semua titik yang terletak pada satah hadapan volum keterlihatan mempunyai nilai pseudo-depth -1;
- Semua titik yang terletak pada satah pemotongan jauh volum keterlihatan mempunyai nilai pseudo-depth 1;
- Semua serpihan yang terletak di dalam isipadu keterlihatan mempunyai nilai pseudo-depth dalam julat [-1 1].
Kemungkinan a Dan b perlu dikira. Untuk melakukan ini, kami menggunakan sifat pseudo-depths 3 dan 4. Kami memperoleh sistem dua persamaan dengan dua yang tidak diketahui:
Mari tambahkan kedua-dua bahagian sistem dan darabkan hasilnya dengan hasil fn, di mana f Dan n tidak boleh sama dengan sifar. Kita mendapatkan:
Mari buka kurungan dan susun semula terma supaya hanya bahagian dengan A, dan di sebelah kanan sahaja dengan b:
Mari kita gantikan (6) kepada (5). Mari tukarkan ungkapan kepada pecahan mudah:
Darab kedua-dua belah dengan -2fn, di mana f Dan n tidak boleh sama dengan sifar. Marilah kita membentangkan yang serupa, menyusun semula istilah dan nyatakan b:
Mari kita gantikan (7) kepada (6) dan nyatakan a:
Sehubungan itu komponen a Dan b adalah sama:
Sekarang mari kita gantikan pekali yang diperoleh ke dalam matriks bahan kerja (1) dan lihat apa yang berlaku kepada koordinat z untuk titik sewenang-wenangnya dalam ruang homogen pemerhati. Penggantian dilakukan seperti berikut:
Biarkan jarak ke satah pemotongan hadapan n adalah sama dengan 2, dan jarak ke satah keratan jauh f sama dengan 10. Pertimbangkan lima titik dalam ruang homogen pemerhati:
| titik | Maknanya |
Penerangan |
|---|---|---|
| 1 | 1 | Titik terletak di hadapan satah pemotongan hadapan volum keterlihatan. Tidak lulus rasterisasi. |
| 2 | 2 | Titik terletak di tepi hadapan potongan volum keterlihatan. Menjalani rasterisasi. |
| 3 | 5 | Titik terletak di antara tepi keratan hadapan dan tepi keratan jauh volum keterlihatan. Menjalani rasterisasi. |
| 4 | 10 | Titik terletak di tepi jauh potongan volum keterlihatan. Menjalani rasterisasi. |
| 5 | 20 | Titik terletak di luar tepi jauh potongan volum keterlihatan. Tidak lulus rasterisasi. |
Mari kita darab semua titik dengan matriks (8), dan kemudian tukarkan koordinat homogen yang terhasil menjadi Koordinat Cartesian . Untuk melakukan ini, kita perlu mengira nilai komponen homogen baru
Dan
.
Perkara 1:
Perhatikan bahawa koordinat homogen diletakkan dengan betul betul dalam CVV, dan yang paling penting, ujian kedalaman OpenGL kini boleh dilakukan, kerana kedalaman pseudo memenuhi sepenuhnya keperluan ujian.
Dengan koordinat z Kami memikirkannya, mari kita beralih ke koordinat x Dan y. Seperti yang dinyatakan sebelum ini, keseluruhan volum keterlihatan perspektif mesti sesuai dengan CVV. Panjang tepi CVV ialah dua. Sehubungan itu, ketinggian dan lebar isipadu keterlihatan perspektif mesti dimampatkan kepada dua unit konvensional.
Kami mempunyai sudut fovy dan magnitud aspek. Mari nyatakan ketinggian dan lebar menggunakan nilai ini.
nasi. 5. Kelantangan keterlihatan
Daripada Rajah. 5 jelas bahawa:
Kini kita boleh mendapatkan pandangan akhir bagi matriks unjuran perspektif untuk sistem koordinat kidal tersuai yang berfungsi dengan CVV OpenGL:
Ini melengkapkan terbitan matriks.
Beberapa perkataan mengenai DirectX - pesaing utama OpenGL. DirectX berbeza daripada OpenGL hanya dalam dimensi CVV dan kedudukannya. Dalam DirectX, CVV ialah saluran paip selari segi empat tepat dengan panjang sepanjang paksinya x Dan y sama dengan dua, dan sepanjang paksi z panjang adalah sama dengan satu. Julat x Dan y ialah [-1 1], dan julat z sama dengan . Bagi sistem koordinat CVV, DirectX, seperti OpenGL, menggunakan sistem koordinat kidal.
Untuk memaparkan matriks perspektif bagi sistem koordinat tangan kanan tersuai, anda perlu melukis semula Rajah. 2, Rajah 3 dan Rajah 4 dengan mengambil kira arah paksi baharu Z. Pengiraan lanjut adalah sama sepenuhnya, sehingga tanda. Untuk matriks DirectX, sifat pseudo-depth 3 dan 4 diubah suai untuk disesuaikan dengan julat.
Pada ketika ini, topik matriks yang menjanjikan boleh dianggap tertutup.
Dalam grafik komputer, konsep pelbagai matriks ditakrifkan. Ini ialah Matriks Dunia, Matriks Pandangan dan Matriks Unjuran. Menggunakan matriks ini dalam kod sumber Program ini melakukan transformasi matriks pada model. Penjelmaan matriks membayangkan pendaraban setiap bucu objek dengan salah satu matriks, atau lebih tepat pendaraban berurutan semua bucu objek dengan setiap tiga matriks. Pendekatan ini membolehkan anda mewakili model dengan betul dalam ruang tiga dimensi monitor dua dimensi anda. Teknik menghantar model melalui tiga matriks yang disenaraikan mewakili intipati mekanisme untuk bekerja dengan data grafik dalam satah tiga dimensi monitor.
Matriks dunia
Matriks dunia – membolehkan anda melakukan pelbagai transformasi matriks (transformasi dan penskalaan) objek dalam sistem koordinat dunia. Sistem dunia koordinat adalah miliknya sistem tempatan koordinat daripada objek ini, yang dikurniakan setiap objek yang, katakan, telah melalui matriks dunia, kerana setiap bucu mengambil bahagian dalam hasil darab matriks ini.
Sistem koordinat tempatan yang baharu sangat memudahkan transformasi afin bagi objek di angkasa. Contohnya, untuk menggerakkan objek dari kiri bucu atas paparan ke sudut kanan bawah paparan, iaitu, untuk menggerakkan objek permainan di angkasa, anda hanya perlu mengalihkannya titik tempatan rujukan, sistem koordinat ke lokasi baharu. Jika tiada matriks dunia, maka objek ini perlu dipindahkan satu bucu pada satu masa. Oleh itu, sebarang objek, atau lebih tepatnya semua bucu objek ini, melalui matriks transformasi dunia.
Seperti yang dinyatakan, transformasi dunia bagi bucu objek boleh terdiri daripada sebarang gabungan putaran, terjemahan dan penskalaan. Dalam tatatanda matematik, putaran sesuatu bucu di sepanjang paksi X kelihatan seperti ini:
 Matriks dunia
Matriks dunia di mana cos ialah sudut putaran dalam radian.
Memutar bucu di sekeliling paksi Y kelihatan seperti ini:
 Memusingkan satu bucu mengelilingi paksi Y
Memusingkan satu bucu mengelilingi paksi Y Dan putaran di sekeliling paksi Z berlaku mengikut formula berikut:
 putaran mengelilingi paksi Z
putaran mengelilingi paksi Z Terjemahan bucu membolehkan anda mengalihkan bucu ini dengan koordinat x, y, z ke titik baru dengan koordinat baharu x1, y1, z1. Dalam notasi matematik ia kelihatan seperti ini:
X1 = x + Tx y1 = y + Ty z1 = z + Tz
Terjemahan bucu dalam tatatanda matriks kelihatan seperti ini:
 Terjemahan bucu dalam tatatanda matriks
Terjemahan bucu dalam tatatanda matriks dengan Tx, Ty dan Tz ialah nilai offset di sepanjang paksi X, Y dan Z.
Anda boleh menskalakan bucu dalam ruang (alih keluar atau zum masuk) dengan koordinat x, y, z ke titik baharu dengan nilai baharu x1, y1, z1 menggunakan tatatanda berikut:
X1 = x * S y1 = y * S z1 = z * S
Dalam notasi matriks ini dinyatakan seperti berikut:
 Skala Pucuk
Skala Pucuk di mana Sx, Sy, Sz ialah nilai-nilai pekali regangan atau mampatan di sepanjang paksi X, Y, Z.
Semua operasi di atas boleh dilakukan secara manual dalam kod sumber program, iaitu, entri yang diberikan boleh dikira seperti yang saya baru saja menerangkannya. Tetapi secara semulajadi, tiada siapa yang melakukan ini (hampir tiada siapa), kerana DirectX mempunyai sejumlah besar kaedah yang akan melakukan semua operasi di atas untuk anda.
Lihat Matriks
Matriks paparan – menentukan lokasi kamera di angkasa dan merupakan matriks kedua yang mana bucu objek didarab. Matriks ini membantu menentukan arah tontonan pemandangan 3D. Pemandangan tiga dimensi ialah semua yang anda lihat pada skrin monitor. Ia seperti di teater di mana anda duduk di porter atau di galeri dan menonton aksi di atas pentas. Jadi, duduk di porter, anda akan mempunyai satu lokasi kamera, dan duduk di galeri adalah berbeza sama sekali.
Malah, matriks ini membolehkan anda menentukan genre permainan. Sebagai contoh, permainan DOOM orang pertama adalah seperti barisan hadapan porter dalam teater, manakala permainan Warcraft adalah seperti galeri balkoni. Matriks paparan direka untuk menentukan kedudukan kamera di angkasa, dan anda boleh mengalihkan kedudukan kamera ke kiri, kanan, atas, bawah, alihkannya, zum masuk dan sebagainya.
Matriks Unjuran
Matriks unjuran ialah matriks yang lebih kompleks yang mencipta unjuran objek tiga dimensi ke atas satah skrin monitor dua dimensi. Menggunakan matriks ini, kawasan keratan hadapan dan belakang ruang tiga dimensi ditentukan, yang membolehkan anda melaraskan ruang keratan objek yang tidak kelihatan pada skrin, dan pada masa yang sama mengurangkan beban pada pemproses kad video. Rajah menunjukkan mekanisme mengunjurkan objek dalam satah dan memotong ruang.
 Matriks Unjuran
Matriks Unjuran Dalam kuliah terakhir kami bercakap tentang unjuran paling penting yang digunakan dalam geometri affine. Sekarang mari kita teruskan untuk mempertimbangkan geometri perspektif dan beberapa jenis unjuran baharu.
Dalam gambar, lukisan dan skrin, imej kelihatan semula jadi dan betul kepada kita. Imej ini dipanggil perspektif. Sifat mereka sedemikian rupa sehingga objek yang lebih jauh digambarkan pada skala yang lebih kecil, garis selari biasanya tidak selari. Akibatnya, geometri imej ternyata agak rumit, dan gambar siap adalah sukar untuk menentukan saiz bahagian tertentu sesuatu objek.
Unjuran perspektif biasa ialah unjuran pusat pada satah dengan sinar lurus melalui titik, pusat unjuran. Salah satu sinar unjuran adalah berserenjang dengan satah unjuran dan dipanggil yang utama. Titik persilangan sinar ini dan satah unjuran adalah titik utama gambar.
Terdapat tiga sistem koordinat. Biasanya, seorang pengaturcara bekerja dan menyimpan data tentang objek geometri dalam koordinat dunia. Untuk meningkatkan realisme, apabila bersedia untuk memaparkan imej pada skrin, data tentang objek daripada koordinat dunia ditukar kepada melihat koordinat. Dan hanya pada masa imej dipaparkan terus pada skrin paparan, mereka bergerak ke koordinat skrin, iaitu nombor piksel skrin.
Dua sistem pertama boleh digunakan dalam sistem koordinat multidimensi, tetapi yang kedua hanya dalam sistem dua dimensi. Operasi tidak boleh diterbalikkan, iaitu, adalah mustahil untuk memulihkan imej tiga dimensi daripada imej unjuran dua dimensi.
Matriks transformasi perspektif umum
Dalam matriks ini unsur-unsur a, d, e bertanggungjawab untuk penskalaan, m, n, L untuk anjakan, hlm, q, r untuk unjuran, s untuk penskalaan menyeluruh, X untuk putaran.
Untuk penerangan terperinci tentang penjejakan ciri titik, penentukuran kamera dan teknik pembinaan semula objek tiga dimensi adalah perlu untuk memperkenalkan model reka bentuk prospektif dan menerangkan sifat geometri transformasi ini. Titik beberapa imej yang diperoleh menggunakan unjuran perspektif mempunyai hubungan istimewa antara satu sama lain, yang diterangkan oleh geometri epipolar. Model hubungan ini mesti diperiksa secara terperinci, kerana Hampir semua kaedah pembinaan semula tiga dimensi memerlukan penilaian model yang sepadan dan bergantung pada sifatnya.
Adalah perlu untuk mengambil perhatian secara berasingan andaian bahawa semua imej sumber menangkap pemandangan yang sama, i.e. setiap imej ialah pandangan pemandangan dari kamera tertentu. Oleh itu, untuk kemudahan penerangan, konsep pandangan diperkenalkan, sebagai imej dengan model kamera yang berkaitan dari mana ia diperoleh.
Unjuran perspektif
Model unjuran perspektif sepadan dengan kamera lubang jarum yang ideal. Model ini agak sepadan dengan proses pembinaan imej dalam kebanyakan kamera foto dan video moden. Walau bagaimanapun, disebabkan oleh batasan optik moden, proses sebenar agak berbeza daripada model kamera lubang jarum. Perbezaan antara proses sebenar dan model dipanggil herotan dan dimodelkan secara berasingan.
Model kamera lubang jarum yang paling ringkas adalah mudah kerana ia diterangkan sepenuhnya oleh pusat unjuran dan kedudukan satah imej. Oleh itu, unjuran mana-mana titik pemandangan dalam imej boleh didapati sebagai persilangan sinar yang menghubungkan pusat unjuran dan titik pemandangan dengan satah imej.
Model unjuran perspektif yang paling mudah
Mari kita pertimbangkan kes paling mudah apabila pusat unjuran kamera (fokus) diletakkan pada asal sistem koordinat, dan satah imej bertepatan dengan satah Z=1. Biarkan (X,Y,Z) ialah koordinat titik dalam ruang 3 dimensi dan (x,y) ialah unjuran titik ini pada imej I. Unjuran perspektif dalam kes ini diterangkan oleh persamaan berikut:
Dalam bentuk matriks menggunakan koordinat homogen, persamaan ini ditulis semula seperti berikut:
 (2.2)
(2.2)
Satah yang terletak pada jarak 1 dari pusat unjuran dan berserenjang dengan paksi optik dipanggil satah imej ideal. Paksi optik memotong satah imej ideal pada titik c, dipanggil titik utama. Ilustrasi kes unjuran perspektif yang paling mudah ditunjukkan dalam Rajah. 1.
Penentukuran kamera dalaman
Kes unjuran perspektif yang paling mudah hampir selalu tidak sepadan dengan kamera sebenar. Jarak dari pusat unjuran ke satah imej, i.e. panjang fokus, dilambangkan dengan f, biasanya tidak sama dengan 1. Juga, koordinat titik dalam satah imej mungkin tidak bertepatan dengan koordinat mutlak. menggunakan kamera digital, hubungan antara koordinat titik dalam imej dan koordinat mutlak titik pada satah ideal, ditentukan oleh bentuk dan saiz piksel matriks.

Mari kita nyatakan dimensi piksel matriks kamera digital sebagai p x , p y , sudut kecenderungan piksel sebagai α , dan titik utama sebagai , Rajah 2. Kemudian koordinat titik (x,y) dalam imej yang sepadan dengan titik (x R , y R) pada satah ideal ditentukan oleh ungkapan:
 (2.3)
(2.3)
Jika f x ,f y ialah panjang fokus f, diukur dalam lebar dan ketinggian piksel, dan tan(α)*f/p y dilambangkan sebagai s, maka formula 2.3 diubah menjadi:
 (2.4)
(2.4)
Matriks K dipanggil matriks penentukuran dalaman kamera. Dalam kebanyakan kes, dalam kamera digital sebenar sudut piksel adalah hampir dengan lurus, i.e. parameter s=0, dan lebar dan tinggi piksel adalah sama. Titik prinsip biasanya terletak di tengah-tengah imej. Oleh itu, matriks K boleh ditulis sebagai:
 (2.5)
(2.5)
Andaian tentang bentuk matriks K ini digunakan secara meluas untuk memudahkan algoritma untuk menentukan penentukuran dalaman kamera, serta dalam pemodelan imej sintetik yang diperlukan untuk menilai kualiti dan kecekapan kaedah pembinaan semula 3D.

Penentukuran kamera luaran
Biarkan M menjadi titik pemandangan dalam ruang 3 dimensi. Sebarang pergerakan adalah transformasi ruang Euclidean, oleh itu dalam koordinat homogen ia dinyatakan sebagai:
 (2.6)
(2.6)
di mana R ialah matriks putaran, T= T ialah vektor terjemahan.
Pergerakan kamera berbanding dengan tempat kejadian adalah bersamaan dengan pergerakan terbalik titik pemandangan berbanding kamera, oleh itu ia adalah sama dengan:
 (2.7)
(2.7)
di mana R, T ialah matriks putaran dan vektor pergerakan kamera berbanding dengan tempat kejadian. Matriks C dipanggil matriks penentukuran luaran kamera. Matriks C -1 dipanggil matriks pergerakan kamera. Oleh itu, matriks penentukuran kamera luaran menterjemahkan koordinat titik pemandangan daripada sistem koordinat pemandangan kepada sistem koordinat yang berkaitan dengan kamera.
Model Unjuran Perspektif Lengkap
Daripada ungkapan 2.1, 2.4, 2.7, kita boleh memperoleh ungkapan untuk unjuran perspektif sewenang-wenangnya untuk mana-mana kamera dengan orientasi dan kedudukan sewenang-wenang dalam ruang:

Dalam bentuk yang lebih ringkas, dengan mengambil kira notasi sebelumnya, formula ini boleh ditulis sebagai:

Matriks P dipanggil matriks unjuran kamera.
Dengan analogi dengan transformasi perspektif umum, mari kita pertimbangkan dahulu kes paling mudah bagi transformasi perspektif satah. Biarkan satah p bertepatan dengan satah Z=0, maka koordinat tiga dimensi homogen mana-mana titiknya ialah M=. Untuk mana-mana kamera dengan matriks unjuran P, transformasi perspektif satah diterangkan oleh matriks 3*3:


Memandangkan mana-mana satah dalam ruang 3-dimensi boleh dipindahkan ke satah Z = 0 dengan transformasi Euclidean bagi putaran dan terjemahan, yang bersamaan dengan mendarab matriks kamera P dengan matriks transformasi L, maka paparan perspektif satah sewenang-wenang dalam ruang diterangkan oleh transformasi linear dengan matriks 3*3.
Transformasi satah perspektif juga dipanggil homografi. Dalam bentuk matriks, transformasi perspektif satah ditulis sebagai m=HM.

Geometri dua imej
Pemandangan yang ditangkap dalam semua imej sumber dianggap tidak bergerak, oleh itu kedudukan relatif unjuran titik adegan pada bingkai yang berbeza tidak boleh berubah dengan cara sewenang-wenangnya. Sekatan yang dikenakan ke atas lokasi unjuran titik jelas bergantung pada parameter kamera dan kedudukannya secara relatif antara satu sama lain. Oleh itu, menentukan model sekatan tersebut memberikan beberapa maklumat tentang kedudukan relatif kamera dari mana imej diperoleh.
Transformasi satah perspektif
Jika pusat kedua-dua kamera bertepatan, maka titik-titik pada satah imej kedua-dua kamera diterjemahkan ke dalam satu sama lain melalui transformasi perspektif satah. Dalam kes ini, transformasi titik antara imej tidak bergantung pada bentuk pemandangan 3 dimensi, tetapi hanya bergantung pada kedudukan relatif satah imej.

Jika keseluruhan adegan atau sebahagian daripadanya adalah pesawat, maka imejnya dihidupkan jenis yang berbeza dengan pusat kamera yang tidak bertepatan boleh ditukar kepada satu sama lain dengan transformasi homografi. Biarkan p ialah satah yang diperhatikan, H 1 ialah penjelmaan homografi antara satah p dan imej saya 1, H 2 - penjelmaan homografi antara satah p dan imej saya 2. Kemudian penjelmaan homografi H 12 antara imej saya 1 Dan saya 2 boleh dikeluarkan seperti berikut:

H 12 tidak bergantung pada parameterisasi satah p, dan oleh itu tidak bergantung pada sistem koordinat dalam ruang
Kebanyakan kaedah untuk menentukan koordinat titik 3D daripada unjuran mereka dan kaedah untuk membina semula pemandangan 3D adalah berdasarkan andaian bahawa pusat kamera bergerak antara pandangan. Oleh itu, jika pusat kamera beberapa jenis bertepatan, kaedah ini akan memberikan hasil yang salah. Konfigurasi kamera sedemikian mesti dikesan dan dikendalikan dengan cara yang istimewa.

Oleh kerana penjelmaan homografi ditulis dalam koordinat homogen, matriks H ditakrifkan mengikut skala. Ia mempunyai 8 darjah kebebasan, dan diparameterkan oleh 8 pembolehubah. Setiap pasangan mata sepadan yang diketahui m 1 Dan m 2 dalam imej pertama dan kedua masing-masing memberikan 2 persamaan linear daripada unsur-unsur matriks H. Oleh itu, 4 pasangan titik sepadan yang diketahui adalah mencukupi untuk menyusun sistem persamaan linear bagi 8 persamaan dengan 8 tidak diketahui. Menurut sistem ini, homografi H boleh ditentukan secara unik jika tiada tiga titik terletak pada garis yang sama.
Matriks Asas
Mari kita pertimbangkan kes apabila pusat kedua-dua jenis kamera tidak bertepatan. biarlah C 1 Dan C 2- pusat dua kamera, M - titik 3 dimensi tempat kejadian, m 1 Dan m 2- unjuran titik M pada imej pertama dan kedua, masing-masing. Biarkan P ialah satah yang melalui titik M dan pusat-pusat kamera C 1 Dan C 2. Satah P memotong satah imej pandangan pertama dan kedua sepanjang garis lurus l 1 Dan l 2. Sejak sinaran C 1 M Dan C 2 M terletak pada satah P, maka jelaslah bahawa titik-titik itu m 1 Dan m 2 berbaring di atas garis lurus l 1 Dan l 2 masing-masing. Kita boleh memberikan pernyataan yang lebih umum bahawa unjuran mana-mana titik M" yang terletak dalam satah P pada kedua-dua imej mesti terletak pada garis lurus l 1 Dan l 2. Garisan ini dipanggil garisan epipolar. Satah P dipanggil satah epipolar.

Dua paparan adegan yang sama dipanggil pasangan stereo, dan segmen C 1 C 2, menyambungkan pusat kamera dipanggil asas pasangan stereo (garis dasar) atau asas stereo. Mana-mana satah epipolar melalui segmen C 1 C 2. biarlah C 1 C 2 memotong imej pertama dan kedua pada titik e 1 Dan e 2 masing-masing. mata e 1 Dan e 2 dipanggil titik epipolar atau epipol. Semua garis epipolar bersilang pada titik e 1 Dan e 2 dalam imej pertama dan kedua masing-masing. Set satah epipolar ialah rasuk yang bersilang di sepanjang tapak stereo C 1 C 2. Banyak garisan epipolar dalam kedua-dua imej juga mewakili berkas garis lurus yang bersilang di e 1 Dan e 2 .
mata m 1 Dan m 2 dipanggil sepadan jika ia adalah unjuran titik pemandangan yang sama M. Garisan epipolar l 1 Dan l 2 dipanggil sepadan jika mereka terletak pada satah epipolar yang sama P. Jika satah epipolar P melalui satu titik m 1, kemudian garis epipolar l 1 Dan l 2, berbaring di dalamnya dipanggil sepadan dengan titik m 1.

Sekatan pada kedudukan mata yang sepadan m 1 Dan m 2, yang mengikuti dari geometri epipolar, boleh dirumuskan seperti berikut: titik m 2, sepadan m 1, mesti terletak pada garis epipolar l 2, sepadan m 1. Keadaan ini dipanggil kekangan epipolar. Dalam koordinat homogen, keadaan bahawa titik m terletak pada talian l ditulis sebagai l T m=0. Garis epipolar juga melalui titik epipolar. Persamaan garis yang melalui titik m 1 Dan e 1 boleh ditulis sebagai:
l 1∼ x m 1,
di mana x- matriks antisimetri berdimensi 3*3 supaya, x m 1- produk vektor m 1 Dan e 1.
Untuk garisan epipolar yang sepadan l 1 Dan l 2 betul:

di mana P+- pseudoinversion bagi matriks P.
Matriks F dipanggil matriks asas. Dia mewakili operator linear, sepadan dengan setiap titik m 1 garis epipolar yang sepadan l 2. Bagi setiap pasangan mata yang sepadan m 1 Dan m 2 betul
m T 2 Fm 1 =0
Ini adalah rumusan kekangan epipolar melalui matriks asas.
Matriks asas mempunyai 7 darjah kebebasan. Setiap pasangan mata yang sepadan m 1 Dan m 2 mentakrifkan satu persamaan linear untuk unsur-unsur matriks, jadi ia boleh dikira daripada 7 pasangan titik sepadan yang diketahui.
Kekangan epipolar adalah sah untuk mana-mana pasangan titik sepadan yang terletak pada satah ideal dua jenis. Jika matriks penentukuran dalaman diketahui K 1 Dan K2 kamera kedua-dua jenis, maka kekangan epipolar untuk titik yang sepadan pada satah ideal ditulis sebagai:

Matriks E dipanggil ketara matriks. Ia boleh ditunjukkan bahawa matriks penting juga boleh didapati daripada kedudukan relatif kamera.
biarlah P 1 =(I|0) Dan P 2 =(R|-RT)- dua matriks reka bentuk dengan penentukuran K = I. Kemudian persamaan reka bentuk untuk satah ideal kedua-dua kamera ditulis dalam bentuk:

Mari cari garis epipolar dalam pandangan kedua yang sepadan dengan titik m" 1 pada yang pertama. Untuk melakukan ini, cukup untuk menayangkan pada pandangan kedua dua mata yang terletak pada sinar (C 1 ,m" 1) ke pandangan kedua, contohnya bahagian tengah kamera pertama (0,0,0,1) T dan satu titik pada satah infiniti (x" 1 ,y" 1 ,z" 1 ,0) T. Unjuran mata ini ialah -RT, dan R(x" 1 ,y" 1 ,z" 1 ,0) T. Persamaan Garis Epipolar l 2, melalui kedua-dua titik ini diberikan sebagai produk vektor:
l 2 =RT×R(x" 1 ,y" 1 ,z" 1) T =R(T×(x" 1 ,y" 1 ,z" 1) T)
Dalam bentuk matriks, vektor bukan produk T×(x" 1 ,y" 1 ,z" 1) T boleh ditulis menggunakan matriks S:

Kemudian kekangan epipolar pada titik dalam satah ideal ditulis sebagai:

Menyatakan matriks penting dari segi parameter penentukuran luaran kedua-dua kamera digunakan untuk mengira kedudukan relatif kamera.

Sifat geometri tiga atau lebih imej
biarlah C 1,C 2 Dan C 3- pusat tiga pandangan pemandangan tiga dimensi yang sama. Dalam kes ini, kekangan epipolar dikenakan pada titik yang sepadan bagi mana-mana pasangan spesies. Jika unjuran dua titik diketahui m 1 Dan m 2 kepada pandangan pertama dan kedua, maka kedudukan unjuran kepada imej ketiga boleh didapati sebagai persilangan dua pandangan epipolar sepadan dengan titik m 1 Dan m 2.
Mengikut dua unjuran yang diketahui m 1 Dan m 2 Menggunakan dua imej dengan penentukuran yang diketahui, seseorang boleh menentukan kedudukan titik M dalam ruang. Oleh itu, jika penentukuran imej ketiga diketahui, maka unjuran titik M ke pandangan ketiga boleh ditentukan dengan unjuran mudah.
Kekangan yang dikenakan pada kedudukan titik yang sepadan dalam lebih daripada dua imej juga boleh ditulis bentuk linear. Untuk tiga jenis, sekatan ini ditulis dalam bentuk tensor trifokal, untuk empat jenis - dalam bentuk tensor quadrifocal. Walau bagaimanapun, pengiraan kekangan ini adalah bersamaan dengan pengiraan tolok bagi ketiga-tiga atau empat pandangan dalam ruang projektif. Jenis sekatan ini tidak digunakan dalam kerja ini dan oleh itu tidak dibincangkan dengan lebih terperinci.