5. Litar elektrik linear dalam mod pengaruh tidak harmonik berkala. Teori litar elektrik

5. Litar elektrik linear dalam mod pengaruh tidak harmonik berkala

5.1. Isyarat berkala tidak harmonik

Apabila menghantar maklumat melalui saluran komunikasi dalam proses penukaran isyarat dalam pelbagai peranti, sebagai peraturan, ayunan bukan harmonik digunakan, kerana ayunan harmonik semata-mata tidak boleh menjadi pembawa maklumat. Untuk menghantar mesej, mereka memodulasi ayunan harmonik dalam amplitud - modulasi amplitud (AM), frekuensi - modulasi frekuensi (FM) atau fasa - modulasi fasa (PM), atau menggunakan isyarat nadi yang dimodulasi dalam amplitud - modulasi amplitud nadi (PAM), lebar. – modulasi lebar nadi (PWM), kedudukan masa – modulasi nadi masa (TPM). Terdapat isyarat lain yang lebih kompleks yang dihasilkan mengikut undang-undang khas. Satu ciri tersendiri bagi isyarat ini ialah watak tidak harmonik yang kompleks. Arus dan voltan yang dijana dalam pelbagai nadi dan peranti digital mempunyai bentuk bukan sinusoidal (19. Isyarat dan litar diskret), isyarat harmonik yang melalui pelbagai peranti tak linear memperoleh sifat bukan sinusoidal (11. Litar elektrik tak linear di bawah pengaruh harmonik), dsb. Semua ini membawa kepada keperluan untuk membangunkan kaedah khas untuk analisis dan sintesis litar elektrik di bawah pengaruh arus dan voltan berkala bukan sinusoidal dan bukan berkala. Kaedah ini adalah berdasarkan perwakilan spektrum pengaruh bukan sinus, berdasarkan pengembangan dalam siri atau kamiran Fourier.

Daripada analisis matematik diketahui bahawa fungsi takharmonik berkala f(t), yang memenuhi syarat Dirichlet, boleh dikembangkan menjadi siri Fourier:
(5.1)
di mana a k,b k - pekali pengembangan ditentukan oleh persamaan
(5.2)

Magnitud mewakili nilai purata fungsi sepanjang tempoh f(t) dan dipanggil komponen malar.

Dalam kajian teori, bukannya formula (5.1), mereka biasanya menggunakan satu lagi berdasarkan menggantikan pembolehubah bebas:
(5.3)
di mana
(5.4)

Persamaan (5.3) ialah bentuk trigonometri bagi siri Fourier. Apabila menganalisis litar, selalunya lebih mudah untuk menggunakan bentuk kompleks siri Fourier, yang boleh didapati daripada (5.3) menggunakan formula Euler:
(5.5)

Menggantikan (5.5) ke dalam persamaan (5.3), selepas penjelmaan mudah kita memperoleh bentuk kompleks siri Fourier:
(5.6)
di mana A k- amplitud kompleks k harmonik ke:
(5.7)
di mana – amplitud; – fasa awal k harmonik ke.

Menggantikan nilai a k Dan b k dari (5.4) hingga (5.7), kami memperoleh:
(5.8)

Set amplitud 0.5 A k = 0,5A –k dalam pengembangan (5.6), diplot terhadap frekuensi positif dan negatif yang sepadan, membentuk simetri berkenaan dengan paksi koordinat (disebabkan oleh pariti pekali dan k) spektrum amplitud garis.

Set ordinat k = – –k daripada (5.7), termasuk dalam pengembangan (5.6) dan diplot terhadap frekuensi positif dan negatif yang sepadan, membentuk relatif simetri kepada asal paksi koordinat (disebabkan oleh keganjilan pekali b k)spektrum fasa garis.

Pengembangan (5.3) boleh dipersembahkan dalam bentuk lain. Mempertimbangkan itu dan k = A k cos k Dan b k= A k dosa k, kemudian selepas penggantian ke (5.3) kita dapat:
(5.9)

Jika kita menganggap komponen pemalar 0/2 sebagai harmonik sifar dengan fasa awal 0 = 0, maka pengembangan (5.9) akan mengambil bentuk
(5.10)

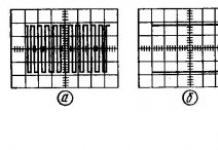
Dalam kes khas apabila fungsi f(a) simetri tentang paksi ordinat (Rajah 5.1, A), pengembangan (5.3) hanya akan mengandungi harmonik genap (kosinus):

(5.11)

dan dengan simetri f(a) relatif kepada asal (Rajah 5.1, b) harmonik ganjil
(5.12)

Apabila mengalihkan asal fungsi f(a) spektrum amplitudnya tidak berubah, tetapi hanya spektrum fasa sahaja yang berubah. Sesungguhnya, mari kita beralih fungsi f(a) sepanjang paksi masa ke kiri oleh t 0 dan menandakan .

Kemudian pengembangan (5.9) akan mengambil bentuk
(5.13)

Contoh. Kembangkan getaran segi empat tepat ke dalam siri Fourier (Rajah 5.1, b). Mempertimbangkan itu f(a) adalah simetri berkenaan dengan asal koordinat dalam pengembangan (5.3) hanya harmonik sinusoidal (5.12) akan kekal, di mana b k akan ditentukan mengikut (5.4):

Menggantikan b k dalam (5.12), kita memperoleh pengembangan siri Fourier:
(5.14)

Seterusnya kita bergerak f(a) p/2 ke kiri (lihat Rajah 5.1, A). Kemudian, mengikut (5.13), kita dapat

(5.15)

Iaitu, kami memperoleh pengembangan dalam komponen kosinus seperti yang sepatutnya untuk isyarat simetri berkenaan dengan paksi ordinat.

Dalam beberapa kes, apabila fungsi berkala f(a) diberikan secara grafik dan mempunyai bentuk yang kompleks; pengembangannya kepada siri Fourier boleh dijalankan menggunakan kaedah analisis grafik. Intipatinya ialah tempoh isyarat T(Rajah 5.2) dibahagikan kepada m selang sama dengan , dan titik putus f(a) tidak boleh jatuh di tengah-tengah kawasan pembahagian; tentukan nilai isyarat f(a n) di tengah-tengah setiap bahagian partition.

Cari pekali pengembangan dan k Dan b k dengan menggantikan kamiran dalam (5.2) dengan jumlah terhingga
(5.16)

Persamaan (5.16) mudah diprogramkan semasa mengira dan k Dan b k, boleh digunakan oleh komputer.

5.2. RMS, nilai purata dan kuasa isyarat bukan harmonik berkala

Untuk kepastian, mari kita anggap itu f(t) mempunyai maksud semasa i(t). Kemudian nilai berkesan arus takharmonik berkala ditentukan mengikut (3.5), di mana i(t) ditentukan oleh persamaan (5.10):
(5.17)

Menggantikan nilai semasa ini kepada (3.5), selepas penyepaduan kami perolehi
(5.18)

iaitu nilai berkesan arus bukan harmonik berkala saya ditentukan sepenuhnya oleh nilai berkesan harmoniknya saya k dan tidak bergantung pada fasa awal mereka k.

Begitu juga, kita dapati nilai berkesan voltan bukan sinus berkala:
(5.19)

Nilai semasa purata ditentukan mengikut ungkapan umum (3.9). Lebih-lebih lagi, mereka biasanya mengambil nilai purata i(t) dalam nilai mutlak
(5.20)

Ditakrifkan sama U rujuk(2) .

Dari sudut pandangan teori litar, purata kuasa aktif isyarat bukan harmonik dan pengedarannya antara harmonik individu adalah sangat menarik.

Kuasa aktif purata bagi isyarat bukan sinus berkala
(5.21)
di mana
(5.22)

k- peralihan fasa antara arus dan voltan k harmonik ke.

Menggantikan nilai i(t) Dan u(t) daripada (5.22) ke dalam persamaan (5.21), selepas penyepaduan kita perolehi:
(5.23)
iaitu, purata kuasa aktif isyarat bukan harmonik berkala sepanjang tempoh adalah sama dengan jumlah kuasa harmonik individu. Formula (5.23) adalah salah satu bentuk yang diketahui secara meluas Persamaan Parseval.

Begitu juga, kita dapati kuasa reaktif
(5.24)
dan kuasa penuh
(5.25)

Perlu ditekankan bahawa, berbeza dengan isyarat harmonik, untuk isyarat bukan harmonik
(5.26)

Magnitud P tuntutan = dipanggil kuasa herotan dan mencirikan tahap perbezaan dalam bentuk semasa i(t) dan voltan u(t).

Sebagai tambahan kepada kuasa herotan, isyarat bukan harmonik berkala dicirikan oleh beberapa ciri lain: pekali:kuasa, k m = P/S; bentuk K f = U/U cf(2); amplitud K a = U m /U; herotan k dan = U 1 /U; harmonik k g = dan sebagainya.

Untuk isyarat sinusoidal k f = /21.11; k a = 1.41; k u = 1; k g = 0.

5.3. Spektrum isyarat bukan harmonik berkala

Pertimbangkan urutan denyutan segi empat tepat yang ditunjukkan dalam Rajah. 5.3, A. Isyarat bentuk ini digunakan secara meluas dalam kejuruteraan radio dan telekomunikasi: telegrafi, sistem penghantaran digital, sistem komunikasi berbilang saluran dengan pembahagian masa, pelbagai nadi dan peranti digital, dsb. (lihat Bab 19). Urutan nadi dicirikan oleh parameter utama berikut: amplitud nadi A dan dan boleh mempunyai maksud kedua-dua voltan dan arus.">, tempohnya t dan dan tempoh berikutnya T. Nisbah tempoh T kepada tempoh t dan dipanggil kitaran tugas denyutan dan dilambangkan dengan q = T/t dan. Lazimnya, nilai kitaran tugas nadi berjulat daripada beberapa unit (dalam teknologi pengukuran, penghantaran diskret dan peranti pemprosesan maklumat) kepada beberapa ratus atau ribuan (dalam radar).

Untuk mencari spektrum jujukan denyutan segi empat tepat, kami menggunakan siri Fourier dalam bentuk kompleks (5.6). Amplitud kompleks k harmonik ke adalah sama mengikut (5.8) selepas kembali kepada pembolehubah asal t.

(5.27)

Menggantikan nilai A k ke dalam persamaan (5.6), kita memperoleh pengembangan siri Fourier:
(5.28)

Dalam Rajah. 5.4 menunjukkan spektrum amplitud kompleks untuk q= 2 dan q= 4. Seperti yang dapat dilihat daripada rajah, spektrum jujukan denyutan segi empat tepat ialah spektrum diskret dengan sampul surat (garis putus-putus dalam Rajah 5.4), yang diterangkan oleh fungsi
(5.29)
dipanggil fungsi pensampelan (lihat Bab 19). Bilangan garis spektrum antara titik rujukan sepanjang paksi frekuensi dan sifar pertama sampul surat adalah sama dengan q- 1. Komponen DC isyarat (nilai purata) , dan nilai berkesan A= , iaitu Semakin tinggi kitaran tugas, semakin rendah tahap komponen DC dan nilai berkesan isyarat. Dengan kitaran tugas yang semakin meningkat q bilangan komponen diskret meningkat - spektrum menjadi lebih padat (lihat Rajah 5.4, b), dan amplitud harmonik berkurangan dengan lebih perlahan. Perlu ditekankan bahawa, selaras dengan (5.27), spektrum urutan yang dipertimbangkan bagi denyutan segi empat tepat adalah nyata.

Daripada spektrum amplitud kompleks (5.27) kita boleh membezakan amplitud A k = |A k| dan spektrum fasa k= arg A k, ditunjukkan dalam Rajah. 5.5 untuk kes q= 4. Daripada angka-angka itu jelas bahawa spektrum amplitud adalah genap, dan spektrum fasa ialah fungsi frekuensi ganjil. Selain itu, fasa harmonik individu mengambil sama ada nilai sifar antara nod, di mana sinus adalah positif, atau ±, di mana sinus adalah negatif (Rajah 5.5, b)

Berdasarkan formula (5.28), kita memperoleh bentuk trigonometri pengembangan siri Fourier dalam harmonik genap (bandingkan dengan (5.15)):
(5.30)

Apabila jujukan nadi dianjak sepanjang paksi masa (Rajah 5.2, b) mengikut (5.13), spektrum amplitudnya akan kekal sama, tetapi spektrum fasanya akan berubah:
(5.31)

Dalam kes apabila jujukan berkala mempunyai bentuk kekutuban yang berbeza (lihat Rajah 5.1), tidak akan ada komponen tetap dalam spektrum (bandingkan (5.30) dan (5.31) dengan (5.14) dan (5.15)).

Dengan cara yang sama, anda boleh mengkaji komposisi spektrum isyarat bukan harmonik berkala dengan bentuk yang berbeza. Jadual 5.1 menunjukkan pengembangan siri Fourier bagi beberapa isyarat yang paling biasa.

Jadual 5.1

	Jenis isyarat	Pengembangan siri Fourier
1
2
3
4
5
6

5.4. Pengiraan litar di bawah pengaruh tidak harmonik berkala

Pengiraan litar elektrik linear di bawah pengaruh isyarat bukan harmonik berkala adalah berdasarkan prinsip superposisi. Intipatinya, seperti yang digunakan pada pengaruh bukan harmonik, adalah untuk mengembangkan isyarat berkala bukan harmonik ke dalam salah satu bentuk siri Fourier (lihat 5.1. Isyarat berkala bukan harmonik. Pengembangan siri Fourier) dan menentukan tindak balas litar daripada setiap harmonik secara berasingan. Tindak balas yang terhasil didapati oleh superposisi (pengenaan) tindak balas separa yang terhasil. Oleh itu, pengiraan litar di bawah pengaruh bukan harmonik berkala termasuk tugas menganalisis komposisi spektrum isyarat (mengembangkannya menjadi siri Fourier), mengira litar daripada setiap komponen harmonik dan tugas sintesis, akibatnya isyarat keluaran yang terhasil ditentukan sebagai fungsi masa (frekuensi) atau berkesannya (nilai amplitud).

Apabila menyelesaikan masalah analisis, mereka biasanya menggunakan bentuk trigonometri (5.3) atau kompleks (5.6) siri Fourier dengan bilangan istilah pengembangan yang terhad, yang membawa kepada beberapa ralat dalam penghampiran isyarat sebenar. Pekali pengembangan a k Dan b k dalam (5.3) atau A k Dan k dalam (5.6) ditentukan menggunakan persamaan (5.4), (5.7) dan (5.8). Dalam kes ini, isyarat input f(a) mesti dinyatakan secara analitikal. Jika isyarat dinyatakan secara grafik, contohnya dalam bentuk osilogram, maka untuk mencari pekali pengembangan a k Dan b k anda boleh menggunakan kaedah grafik-analisis (lihat (5.16)).

Pengiraan litar daripada harmonik individu biasanya dijalankan menggunakan kaedah simbolik. Walau bagaimanapun, perlu diingat bahawa k ke tindak balas induktif harmonik XL(k) = kL, dan kemuatan X C(k) = 1/(kС), iaitu pada k reaktans induktif harmonik ke dalam k kali lebih banyak, dan kapasitif masuk k kali kurang daripada pada harmonik pertama. Ini, khususnya, menerangkan hakikat bahawa harmonik tinggi lebih ketara dalam kapasitansi, dan kurang jelas dalam induktansi, daripada voltan yang digunakan padanya. Rintangan aktif R pada frekuensi rendah dan sederhana boleh dianggap bebas daripada frekuensi.

Selepas menentukan arus dan voltan yang diperlukan daripada harmonik individu, tindak balas litar yang terhasil kepada pengaruh berkala bukan harmonik didapati dengan kaedah superposisi. Dalam kes ini, sama ada nilai serta-merta isyarat yang terhasil ditentukan berdasarkan pengiraan amplitud dan fasa harmonik individu, atau amplitud atau nilai berkesannya mengikut persamaan (5.18), (5.19). Apabila menentukan tindak balas yang terhasil, perlu diingat bahawa, selaras dengan perwakilan ayunan berkala bukan harmonik pada satah kompleks, vektor pelbagai harmonik berputar dengan frekuensi sudut yang berbeza.

Contoh. Kepada litar yang ditunjukkan dalam Rajah. 5.6, voltan digunakan u(t) dalam bentuk denyutan segi empat tepat dengan tempoh ulangan T= 2t dan dan amplitud A dan = 1V (lihat Rajah 5.3, b). Tentukan nilai voltan serta-merta dan berkesan merentas kapasitansi.

Pengembangan voltan ini kepada siri Fourier ditentukan oleh formula (5.31). Mari kita hadkan diri kita kepada tiga sebutan pertama pengembangan (5.31): harmonik kth ialah keadaan litar elektrik yang terdiri daripada unsur reaktif yang berbeza di mana peralihan fasa antara arus masukan dan voltan yang dikenakan. k-x harmonik ialah sifar. Fenomena resonans boleh digunakan untuk mengasingkan harmonik individu daripada isyarat bukan sinus berkala. Perlu ditekankan bahawa litar boleh secara serentak mencapai resonans arus pada satu frekuensi dan resonans voltan pada yang lain.

Contoh. Untuk litar yang ditunjukkan dalam Rajah. 5.7, untuk 1 tertentu, L 1 cari nilai C 1 dan C 2, di mana resonans voltan berlaku serentak pada harmonik pertama dan resonans arus pada harmonik ke-5.

Daripada keadaan resonans voltan, kita dapati bahawa reaktans masukan litar pada harmonik pertama mestilah sifar:
(5.32)

dan pada kelima - infiniti (reaktans input pada harmonik kelima hendaklah sifar):
(5.33)

Daripada keadaan (5.32) dan (5.33) kita dapati nilai kapasitansi yang dikehendaki:

Nota Pengenalan

Bahagian ini akan mengkaji perwakilan isyarat berkala menggunakan siri Fourier. Siri Fourier adalah asas kepada teori analisis spektrum kerana, seperti yang akan kita lihat kemudian, transformasi Fourier bagi isyarat tidak berkala boleh diperolehi dengan membawa siri Fourier ke had pada tempoh pengulangan yang tidak terhingga. Akibatnya, sifat siri Fourier juga sah untuk transformasi Fourier bagi isyarat tidak berkala.

Kami akan mempertimbangkan ungkapan siri Fourier dalam bentuk trigonometri dan kompleks, dan juga memberi perhatian kepada syarat Dirichlet untuk penumpuan siri Fourier. Di samping itu, kami akan membincangkan secara terperinci tentang penjelasan konsep seperti frekuensi negatif spektrum isyarat, yang sering menyebabkan kesukaran apabila menjadi biasa dengan teori analisis spektrum.

Isyarat berkala. Siri Trigonometri Fourier

Biarkan terdapat isyarat berkala masa berterusan yang berulang dengan tempoh c, i.e. , di mana ialah integer arbitrari.

Sebagai contoh, Rajah 1 menunjukkan urutan denyutan segi empat tepat tempoh c, diulang dengan tempoh c.

Rajah 1. Urutan berkala

Denyutan segi empat tepat

Daripada kursus analisis matematik diketahui bahawa sistem fungsi trigonometri

dengan berbilang frekuensi, di mana rad/s ialah integer, membentuk asas ortonormal untuk penguraian isyarat berkala dengan tempoh yang memenuhi syarat Dirichlet.

Syarat Dirichlet untuk penumpuan siri Fourier memerlukan isyarat berkala dinyatakan pada segmen dan memenuhi syarat berikut:

Contohnya, fungsi berkala tidak memenuhi syarat Dirichlet kerana fungsi mempunyai ketakselanjaran jenis kedua dan mengambil nilai tak terhingga pada , dengan integer arbitrari. Jadi fungsinya tidak boleh diwakili oleh siri Fourier. Anda juga boleh memberikan contoh fungsi , yang terhad, tetapi juga tidak memenuhi syarat Dirichlet, kerana ia mempunyai bilangan mata ekstrem yang tidak terhingga apabila ia menghampiri sifar. Graf fungsi ditunjukkan dalam Rajah 2.

Rajah 2. Graf fungsi :

A - dua tempoh pengulangan; b - di kawasan berhampiran

Rajah 2a menunjukkan dua tempoh ulangan bagi fungsi tersebut , dan dalam Rajah 2b - kawasan di sekitar . Ia boleh dilihat bahawa apabila ia menghampiri sifar, kekerapan ayunan meningkat tanpa terhingga, dan fungsi sedemikian tidak boleh diwakili oleh siri Fourier, kerana ia tidak monotonik sekeping.

Perlu diingatkan bahawa dalam praktiknya tidak ada isyarat dengan nilai arus atau voltan tak terhingga. Berfungsi dengan jenis ekstrem yang tidak terhingga juga tidak berlaku dalam masalah yang digunakan. Semua isyarat berkala nyata memenuhi syarat Dirichlet dan boleh diwakili oleh siri Fourier trigonometri tak terhingga dalam bentuk:

Dalam ungkapan (2), pekali menentukan komponen malar bagi isyarat berkala.

Di semua titik di mana isyarat berterusan, siri Fourier (2) menumpu kepada nilai isyarat yang diberikan, dan pada titik ketakselanjaran jenis pertama - kepada nilai purata , di mana dan adalah had di sebelah kiri dan di sebelah kanan titik ketakselanjaran, masing-masing.

Ia juga diketahui daripada kursus analisis matematik bahawa penggunaan siri Fourier terpotong, yang mengandungi hanya sebutan pertama dan bukannya jumlah tak terhingga, membawa kepada perwakilan anggaran isyarat:

yang memastikan minimum ralat kuasa dua min. Rajah 3 menggambarkan penghampiran kereta api gelombang persegi berkala dan gelombang tanjakan berkala apabila menggunakan bilangan sebutan siri Fourier yang berbeza.

Rajah 3. Penghampiran isyarat menggunakan siri Fourier terpotong:

A - denyutan segi empat tepat; b - isyarat gigi gergaji

Siri Fourier dalam bentuk kompleks

Dalam bahagian sebelumnya, kami mengkaji siri Fourier trigonometri untuk pengembangan isyarat berkala sewenang-wenang yang memenuhi syarat Dirichlet. Menggunakan formula Euler, kita boleh menunjukkan:
Kemudian siri Fourier trigonometri (2) dengan mengambil kira (4):

Oleh itu, isyarat berkala boleh diwakili oleh jumlah komponen malar dan eksponen kompleks berputar pada frekuensi dengan pekali untuk frekuensi positif, dan untuk eksponen kompleks berputar pada frekuensi negatif.

Mari kita pertimbangkan pekali untuk eksponen kompleks berputar dengan frekuensi positif:

Ungkapan (6) dan (7) bertepatan; sebagai tambahan, komponen malar juga boleh ditulis melalui eksponen kompleks pada frekuensi sifar:

Oleh itu, (5) mengambil kira (6)-(8) boleh diwakili sebagai jumlah tunggal apabila diindeks daripada tolak infiniti kepada infiniti:

Ungkapan (9) ialah siri Fourier dalam bentuk kompleks. Pekali siri Fourier dalam bentuk kompleks adalah berkaitan dengan pekali siri dalam bentuk trigonometri, dan ditentukan untuk kedua-dua frekuensi positif dan negatif. Subskrip dalam penetapan frekuensi menunjukkan bilangan harmonik diskret, dengan subskrip negatif sepadan dengan frekuensi negatif.

Daripada ungkapan (2) ia mengikuti bahawa untuk isyarat sebenar pekali siri (2) juga nyata. Walau bagaimanapun, (9) mengaitkan isyarat sebenar dengan set pekali konjugat kompleks yang berkaitan dengan kedua-dua frekuensi positif dan negatif.

Beberapa penjelasan siri Fourier dalam bentuk kompleks

Dalam bahagian sebelumnya, kami membuat peralihan daripada siri Fourier trigonometri (2) kepada siri Fourier dalam bentuk kompleks (9). Akibatnya, bukannya mengurai isyarat berkala dalam asas fungsi trigonometri sebenar, kami menerima pengembangan dalam asas eksponen kompleks, dengan pekali kompleks, malah frekuensi negatif muncul dalam pengembangan! Memandangkan isu ini sering disalah ertikan, beberapa penjelasan diperlukan.

Pertama, bekerja dengan eksponen kompleks dalam kebanyakan kes lebih mudah daripada bekerja dengan fungsi trigonometri. Sebagai contoh, apabila mendarab dan membahagi eksponen kompleks, cukup dengan hanya menambah (menolak) eksponen, manakala formula untuk mendarab dan membahagi fungsi trigonometri adalah lebih rumit.

Membezakan dan menyepadukan eksponen, walaupun yang kompleks, juga lebih mudah daripada fungsi trigonometri, yang sentiasa berubah apabila dibezakan dan disepadukan (sinus bertukar menjadi kosinus dan sebaliknya).

Jika isyarat berkala dan nyata, maka siri Fourier trigonometri (2) kelihatan lebih jelas, kerana semua pekali pengembangan , dan kekal nyata. Walau bagaimanapun, seseorang sering perlu berurusan dengan isyarat berkala yang kompleks (contohnya, apabila memodulasi dan penyahmodulasian, perwakilan kuadratur sampul kompleks digunakan). Dalam kes ini, apabila menggunakan siri trigonometri Fourier, semua pekali , dan pengembangan (2) akan menjadi kompleks, manakala apabila menggunakan siri Fourier dalam bentuk kompleks (9), pekali pengembangan yang sama akan digunakan untuk kedua-dua isyarat input sebenar dan kompleks. .

Dan akhirnya, adalah perlu untuk memikirkan penjelasan tentang frekuensi negatif yang muncul dalam (9). Soalan ini sering menimbulkan salah faham. Dalam kehidupan seharian kita tidak menemui frekuensi negatif. Sebagai contoh, kami tidak pernah menala radio kami kepada frekuensi negatif. Mari kita pertimbangkan analogi berikut dari mekanik. Biarkan terdapat bandul spring mekanikal yang berayun bebas dengan frekuensi tertentu. Bolehkah bandul berayun dengan frekuensi negatif? Sudah tentu tidak. Sama seperti tiada stesen radio yang menyiarkan pada frekuensi negatif, kekerapan ayunan bandul tidak boleh negatif. Tetapi bandul spring ialah objek satu dimensi (bandul berayun sepanjang satu garis lurus).

Kita juga boleh memberikan analogi lain dari mekanik: roda berputar dengan frekuensi . Roda, tidak seperti bandul, berputar, i.e. titik pada permukaan roda bergerak dalam satah, dan tidak hanya berayun sepanjang satu garis lurus. Oleh itu, untuk menentukan secara unik putaran roda, menetapkan kelajuan putaran tidak mencukupi, kerana ia juga perlu untuk menetapkan arah putaran. Inilah sebabnya mengapa kita boleh menggunakan tanda frekuensi.

Jadi, jika roda berputar dengan rad frekuensi / s lawan jam, maka kami menganggap bahawa roda berputar dengan frekuensi positif, dan jika mengikut arah jam, maka kekerapan putaran akan menjadi negatif. Oleh itu, untuk arahan putaran, frekuensi negatif tidak lagi menjadi karut dan menunjukkan arah putaran.

Dan sekarang perkara yang paling penting yang mesti kita fahami. Ayunan objek satu dimensi (contohnya, bandul spring) boleh diwakili sebagai jumlah putaran dua vektor yang ditunjukkan dalam Rajah 4.

Rajah 4. Ayunan bandul spring

Sebagai hasil tambah putaran dua vektor

pada satah kompleks

Bandul berayun di sepanjang paksi sebenar satah kompleks dengan frekuensi mengikut hukum harmonik. Pergerakan bandul ditunjukkan sebagai vektor mendatar. Vektor atas berputar pada satah kompleks dengan frekuensi positif (lawan arah jam), dan vektor bawah berputar dengan frekuensi negatif (mengikut arah jam). Rajah 4 dengan jelas menggambarkan hubungan yang terkenal dari kursus trigonometri:

Oleh itu, siri Fourier dalam bentuk kompleks (9) mewakili isyarat satu dimensi berkala sebagai jumlah vektor pada satah kompleks berputar dengan frekuensi positif dan negatif. Pada masa yang sama, mari kita ambil perhatian bahawa dalam kes isyarat sebenar, menurut (9), pekali pengembangan untuk frekuensi negatif adalah konjugat kompleks kepada pekali sepadan untuk frekuensi positif. Dalam kes isyarat kompleks, sifat pekali ini tidak dipegang kerana fakta bahawa dan juga kompleks.

Spektrum isyarat berkala

Siri Fourier dalam bentuk kompleks ialah penguraian isyarat berkala kepada jumlah eksponen kompleks yang berputar pada frekuensi positif dan negatif dalam gandaan rad/c dengan pekali kompleks sepadan yang menentukan spektrum isyarat. Pekali kompleks boleh diwakili menggunakan formula Euler sebagai , di mana adalah spektrum amplitud, a ialah spektrum fasa.

Memandangkan isyarat berkala dibentangkan dalam satu baris hanya pada grid frekuensi tetap, spektrum isyarat berkala adalah garis (diskrit).

Rajah 5. Spektrum jujukan berkala

Denyutan segi empat tepat:

A - spektrum amplitud; b - spektrum fasa

Rajah 5 menunjukkan contoh amplitud dan spektrum fasa bagi jujukan berkala bagi denyutan segi empat tepat (lihat Rajah 1) pada c, tempoh nadi c dan amplitud nadi B.

Spektrum amplitud isyarat sebenar asal adalah simetri berkenaan dengan frekuensi sifar, dan spektrum fasa adalah antisimetri. Pada masa yang sama, kami perhatikan bahawa nilai spektrum fasa dan sepadan dengan titik yang sama dalam satah kompleks.

Kita boleh membuat kesimpulan bahawa semua pekali pengembangan isyarat yang dikurangkan adalah benar-benar nyata, dan spektrum fasa sepadan dengan pekali negatif.

Sila ambil perhatian bahawa dimensi spektrum amplitud bertepatan dengan dimensi isyarat. Jika ia menerangkan perubahan voltan dari semasa ke semasa, diukur dalam volt, maka amplitud harmonik spektrum juga akan mempunyai dimensi volt.

kesimpulan

Bahagian ini membincangkan perwakilan isyarat berkala menggunakan siri Fourier. Ungkapan bagi siri Fourier dalam bentuk trigonometri dan kompleks diberikan. Kami memberi perhatian khusus kepada syarat Dirichlet untuk penumpuan siri Fourier dan memberikan contoh fungsi yang mana siri Fourier mencapah.

Kami membincangkan secara terperinci tentang ungkapan siri Fourier dalam bentuk kompleks dan menunjukkan bahawa isyarat berkala, kedua-dua nyata dan kompleks, diwakili oleh satu siri eksponen kompleks dengan frekuensi positif dan negatif. Dalam kes ini, pekali pengembangan juga kompleks dan mencirikan amplitud dan spektrum fasa isyarat berkala.

Dalam bahagian seterusnya kita akan melihat dengan lebih terperinci sifat-sifat spektrum isyarat berkala.

Pelaksanaan perisian dalam perpustakaan DSPL

Dötsch, G. Panduan untuk aplikasi praktikal transformasi Laplace. Moscow, Nauka, 1965, 288 hlm.

Analisis litar dalam domain masa dengan kaedah pembolehubah keadaan di bawah pengaruh malar

4.1 Pengembangan siri Fourier bagi jujukan nadi berkala yang diberikan

Gambar rajah litar elektrik, dengan mengambil kira Jadual 1, dibentangkan dalam Rajah. 7.

Mana-mana fungsi berkala f(t) yang memenuhi syarat Dirichlet boleh dikembangkan menjadi siri Fourier. Mari kita nyatakan tempoh fungsi oleh T, dan kekerapan asas oleh _. Siri Fourier boleh ditulis dalam dua cara.

Borang penyertaan pertama:

Borang rakaman kedua:

Dalam kedua-dua bentuk, A 0 ialah komponen malar bagi siri; Dan k ialah amplitud harmonik kth siri itu; k ialah fasa awal harmonik k;

Daripada formula Euler ia mengikutinya. Oleh itu,

Dengan mengambil kira perkara ini, kita boleh menulis siri Fourier dalam bentuk yang kompleks.

Mari kita cipta ungkapan untuk amplitud kompleks.

Dengan mengambil kira perkara ini, kami memperoleh ungkapan untuk fungsi berkala masa:

Membandingkan ungkapan yang terhasil dengan formula (12), kita memperoleh:

Dalam hal ini, dalam kes kami, adalah mungkin untuk mendapatkan pekali untuk bentuk elektrik rakaman siri Fourier daripada nilai amplitud dan spektrum fasa yang diperoleh di bahagian sebelumnya. Kami akan memilih bilangan istilah anggaran dengan mengambil kira lebar spektrum isyarat input.

Amplitud diskret dan spektrum fasa ditunjukkan dalam Rajah 25, 26. Pengiraan mereka diringkaskan dalam Jadual 5.

"kanan">Jadual 5.

Amplitud dan fasa pada harmonik yang sepadan

Harmonik no.

nasi. 25. Spektrum amplitud diskret isyarat input

Pembelahan Andronov-Hopf

Kami diberi sistem: x1=m*x1+ x2+m*x12- x12- x1*x22 x2=- x1+ x22 Variasi pertama nilai bifurkasi > > Semasa penyelesaian, kami memperoleh 4 titik tunggal, pertimbangkan setiap satu dan tentukan jenis mereka. Titik tunggal pertama > > > > > Kami mendapati bahawa pada titik (0...

Matematik Diskret

Biarkan F ialah fungsi binari bagi n pembolehubah. Mari kita andaikan bahawa F tidak sama dengan sifar. Biarkan T1, T2,…, Tk ialah semua titik takrifannya di mana F=1. Ia boleh dibuktikan bahawa formula berikut adalah sah: , di mana, j=1,2,…, k...

Sifat pembezaan fungsi hiperbolik

Mari kita cari pengembangan fungsi hiperbola utama dalam siri Taylor dalam kejiranan titik, i.e. dalam satu siri jenis yang dipanggil siri Maclaurin. Fungsi eksponen dan hiperbolik Biarkan, kemudian untuk sebarang...

Kaedah reka bentuk matematik

Ia dikehendaki melaksanakan pemodelan hingar dengan undang-undang taburan kebarangkalian Rayleigh dan serakan D=12, di mana y=. Untuk mendapatkan realisasi hingar dengan undang-undang taburan tertentu, kaedah fungsi songsang digunakan...

Ruang biasa

Teori interpolasi mempunyai banyak aplikasi dalam teori siri Fourier. Definisi. Biarkan menjadi fungsi berkala sedemikian. Norma dalam ruang ialah nombor, dan pekali Fourier bagi suatu fungsi ialah nombor...

Asas matematik diskret

Teorem 1. Mana-mana fungsi logik boleh diwakili dalam SDNF: , (1) di mana m, dan percanggahan diambil alih semua set nilai 2m bagi pembolehubah x1,...xm. Fungsi f dikembangkan menjadi n-pembolehubah pertama...

Transformasi Fourier dan beberapa aplikasinya

(1) Formula kamiran Fourier. Pertama, kami memperkenalkan konsep nilai utama kamiran. Biarkan fungsi itu boleh disepadukan pada mana-mana segmen garis nombor. Definisi 1.1. Jika terdapat had yang terhad, (1...

Mari kita pertimbangkan sistem. Kami akan membina sistem dengan bahagian genap yang diberikan. Beritahu kami bahagian genap. Mari kita gunakan formula dan mengubahnya Oleh itu, kita boleh menulis Dari sini, mengetahui, kita dapat di mana fungsi pemantulan sistem...

Persamaan trigonometri

Kami mengurangkan persamaan kepada bentuk f(x)=0 dan mewakili bahagian kiri persamaan sebagai hasil darab f1(x)*f2(x)*...* fm(x). Kemudian persamaan ini dikurangkan kepada satu set persamaan: f1(x)=0, f2(x)=0,..., fm(x)=0. Harus diingat...

Persamaan trigonometri dan ketaksamaan

Kaedah pemfaktoran adalah seperti berikut: jika maka setiap penyelesaian kepada persamaan ialah penyelesaian kepada set persamaan. Pernyataan sebaliknya, secara amnya, palsu: tidak setiap penyelesaian kepada set adalah penyelesaian kepada persamaan...

Fungsi Eliptik Jacobi

Oleh kerana, untuk nilai sebenar hujah, fungsi Jacobi snu, cnu, dnu memenuhi syarat teorem Dirichlet, maka siri Fourier yang sepadan boleh dibina untuk mereka. Fungsi f(x) memenuhi syarat Dirichlet dalam selang (?l,l)...

1.3 Membuat kesimpulan umum.

Bahagian 2

Matlamat kerja: mendalami pengetahuan teori yang diperolehi semasa kajian transformasi Fourier(Transformasi Fourier)

Maklumat teori yang diperlukan.

Menukar tempoh T dan tempoh nadi seperti ditunjukkan dalam Rajah. 7, anda boleh menukar spektrum isyarat. Apabila tempoh bertambah, harmonik bergerak lebih rapat tanpa mengubah bentuk sampul surat.

Rajah 7 – Perubahan spektrum

Mari kita simulasi nadi segi empat tepat tunggal, urutan denyutan berkala dengan noktah T Dan 10T .

t = 0:.0314:25; y= persegi(2*pi*t/10, pi*pi); z = rectpuls(2*pi*t1/10); subplot(4,2,1); plot(t,x) subplot(4,2,2); plot(t,y) subplot(4,2,3); plot(t1,z)

Mari kita jalankan analisis spektrum isyarat yang diterima. Proses tidak berkala - ini adalah isyarat maklumat, denyutan tunggal, ayunan huru-hara(bunyi bising) - mempunyai padu atau berterusan spektrum. Secara intuitif, kesimpulan ini boleh dicapai dengan mewakili satu nadi sebagai sebahagian daripada urutan berkala, yang tempohnya meningkat selama-lamanya. Sesungguhnya, apabila selang antara denyutan meningkat, harmonik dalam rajah spektrum jujukan denyutan berkala semakin rapat: semakin kurang kerap denyutan mengikut, semakin kecil jarak antara harmonik bersebelahan (ia bersamaan dengan 1/ T). Spektrum nadi tunggal (kes mengehadkan peningkatan tempoh) menjadi berterusan, dan ia diperkenalkan bukan dalam baris, tetapi Kamiran Fourier.

Transformasi Fourier(Transformasi Fourier) ialah alat analisis spektrum tidak berkala isyarat.

Fungsi yang diterangkan di bawah melaksanakan kaedah Transformasi Fourier Cepat (FFT) khas - Transformasi Fourier Pantas (FFT), yang membolehkan anda mengurangkan secara mendadak bilangan operasi aritmetik semasa transformasi di atas. Kaedah ini amat berkesan jika bilangan elemen yang diproses (sampel) ialah 2n, di mana n ialah integer positif. DALAM MatLab Fungsi berikut digunakan:

fft(X) - mengembalikan transformasi Fourier diskret untuk vektor X, menggunakan algoritma transformasi Fourier pantas jika boleh. Jika X ialah matriks, fungsi fft mengembalikan jelmaan Fourier untuk setiap lajur matriks;

fft(X.n)- mengembalikan transformasi Fourier titik-n. Jika panjang vektor X kurang daripada n, maka elemen yang hilang diisi dengan sifar. Jika panjang X lebih besar daripada n, maka unsur tambahan dikeluarkan. Apabila X ialah matriks, panjang lajur dilaraskan sama;

ft(X,[ Ldirn) dan fft(X,n,malap)- gunakan transformasi Fourier pada salah satu dimensi tatasusunan bergantung pada nilai parameter malap.

Transformasi Fourier songsang satu dimensi adalah mungkin, dilaksanakan oleh fungsi berikut:

ifft(F)- mengembalikan hasil penjelmaan Fourier songsang diskret bagi suatu vektor F . Jika F - matriks, kemudian ifft mengembalikan transformasi Fourier songsang untuk setiap lajur matriks ini;

ifft(F.n)- mengembalikan hasil transformasi Fourier songsang diskret n-titik bagi vektor F ;

ifft(F.,malap) dan = ifft(X,n,malap)- kembalikan hasil transformasi Fourier diskret songsang tatasusunan F mengikut baris atau lajur bergantung pada nilai skalar malap .

Untuk sesiapa X hasil daripada pelaksanaan berurutan bagi transformasi Fourier langsung dan songsang ifft(fft(x)) sama X sehingga ralat pembundaran. Jika X - susunan nombor nyata, ifft(fft(x)) mungkin mempunyai bahagian khayalan yang kecil.

Mari kita dapatkan spektrum isyarat simulasi.

Jom panggil program SPTool (Alat Pemprosesan Isyarat). Mari kita mengimport isyarat simulasi dan mengira spektrum isyarat. Untuk melakukan ini, pilih isyarat dalam senarai isyarat dan tekan butang Buat, terletak di bawah senarai spektrum. Di tingkap Pemapar Spektrum di padang Parameter anda perlu menentukan kaedah analisis spektrum. Kami menentukan kaedah DFT (FFT transformasi Fourier pantas digunakan). Setelah menentukan kaedah, klik pada butang Mohon. Graf ketumpatan spektrum kuasa akan dipaparkan. Adalah mungkin untuk memaparkan spektrum pada skala linear atau logaritma (menu Pilihan).

Spektrum adalah berterusan (pepejal) huru hara(bunyi bising) turun naik. Dalam kes ini, ciri spektrum, sebagai fungsi frekuensi, juga huru hara(rawak) proses, parameter statistik yang ditentukan oleh spesifik proses masa rawak tertentu. Mari jana isyarat yang mengandungi komponen biasa dengan frekuensi 50 Hz dan 120 Hz dan komponen tambahan rawak dengan purata sifar.

TUGASAN 2

Contoh pengembangan siri Fourier.

A) Urutan nadi segi empat tepat .

Rajah 2. Urutan denyutan segi empat tepat.

Isyarat ini adalah fungsi genap dan ia mudah digunakan bentuk sinus-kosinus Siri Fourier:

. (17)

Tempoh denyutan dan tempoh pengulangannya dimasukkan ke dalam formula yang terhasil dalam bentuk nisbah, yang biasanya dipanggil kitaran tugas urutan nadi :.

. (18)

Nilai jangka malar siri, dengan mengambil kira sepadan dengan:

.

Perwakilan urutan denyutan segi empat tepat dalam bentuk siri Fourier mempunyai bentuk:

. (19)

Graf fungsi mempunyai corak lobus.
Dihantar pada ref.rf
Paksi mendatar digradasikan dalam nombor dan frekuensi harmonik.

Rajah 3. Perwakilan jujukan denyutan segi empat tepat

dalam bentuk siri Fourier.

Lebar kelopak, diukur dalam bilangan harmonik, adalah sama dengan kitaran tugas (pada , kita ada , sekiranya ). Ini membayangkan sifat penting spektrum urutan denyutan segi empat tepat - di dalamnya tiada harmonik dengan nombor yang merupakan gandaan kitaran tugas . Jarak frekuensi antara harmonik bersebelahan adalah sama dengan kekerapan ulangan nadi. Lebar cuping, diukur dalam unit frekuensi, ialah , ᴛ.ᴇ. adalah berkadar songsang dengan tempoh isyarat. Kita boleh membuat kesimpulan: semakin pendek nadi, semakin luas spektrumnya .

b) Isyarat ramp .

Rajah 4. Gelombang tanjakan.

Isyarat gigi gergaji dalam tempoh diterangkan oleh fungsi linear

, . (20)

Isyarat ini ialah fungsi ganjil, dan oleh itu siri Fourier dalam bentuk sinus-kosinus hanya mengandungi komponen sinus:

Siri Fourier bagi isyarat gigi gergaji mempunyai bentuk:

Adalah penting untuk ambil perhatian bahawa untuk spektrum isyarat segi empat tepat dan gigi gergaji adalah ciri bahawa amplitud harmonik dengan peningkatan bilangan menurun secara berkadar .

V) Urutan nadi segi tiga .

Siri Fourier mempunyai bentuk:

Rajah 5. Urutan denyutan segi tiga.

Seperti yang dapat kita lihat, berbeza dengan jujukan denyutan segi empat tepat dan gigi gergaji, untuk isyarat berkala segi tiga amplitud harmonik berkurangan mengikut kadar kuasa kedua nombor harmonik. Ini disebabkan oleh fakta bahawa kadar pereputan spektrum bergantung kepada tahap kelancaran isyarat.

Kuliah No 3. Transformasi Fourier.

Sifat-sifat transformasi Fourier.

Contoh pengembangan siri Fourier. - konsep dan jenis. Pengelasan dan ciri kategori "Contoh pengembangan siri Fourier." 2017, 2018.