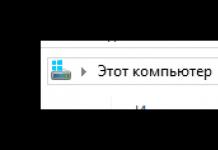
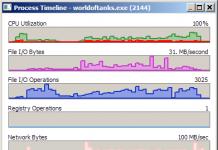
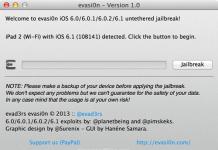
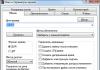
ഉചിതമായ രേഖീയ സംയോജനത്തിലൂടെ ഈ വെക്റ്ററുകളിൽ നിന്ന് ഒരു പൂജ്യം വെക്റ്റർ ലഭിക്കുമെങ്കിൽ, അതേ ക്രമത്തിലുള്ള വെക്റ്ററുകളുടെ ഒരു സിസ്റ്റത്തെ ലീനിയർ ആശ്രിത എന്ന് വിളിക്കുന്നു. (ഒരു രേഖീയ സംയോജനത്തിന്റെ എല്ലാ ഗുണകങ്ങളും പൂജ്യത്തിന് തുല്യമാകുന്നത് അനുവദനീയമല്ല, കാരണം ഇത് നിസ്സാരമായിരിക്കും.) അല്ലാത്തപക്ഷം, വെക്റ്ററുകളെ രേഖീയമായി സ്വതന്ത്രമെന്ന് വിളിക്കുന്നു. ഉദാഹരണത്തിന്, ഇനിപ്പറയുന്ന മൂന്ന് വെക്‌ടറുകൾ:

രേഖീയമായി ആശ്രയിക്കുന്നു, കാരണം അത് പരിശോധിക്കാൻ എളുപ്പമാണ്. ഒരു ലീനിയർ ആശ്രിതത്വത്തിന്റെ കാര്യത്തിൽ, ഏത് വെക്റ്ററും മറ്റ് വെക്റ്ററുകളുടെ രേഖീയ സംയോജനത്തിലൂടെ എല്ലായ്പ്പോഴും പ്രകടിപ്പിക്കാൻ കഴിയും. ഞങ്ങളുടെ ഉദാഹരണത്തിൽ: ഒന്നുകിൽ അല്ലെങ്കിൽ ഇത് ഉചിതമായ കണക്കുകൂട്ടലുകൾ ഉപയോഗിച്ച് പരിശോധിക്കുന്നത് എളുപ്പമാണ്. ഇത് ഇനിപ്പറയുന്ന നിർവചനത്തിലേക്ക് നയിക്കുന്നു: ഈ വെക്റ്ററുകളുടെ ഒരു രേഖീയ സംയോജനമായി പ്രതിനിധീകരിക്കാൻ കഴിയുന്നില്ലെങ്കിൽ ഒരു വെക്റ്റർ മറ്റ് വെക്റ്ററുകളിൽ നിന്ന് രേഖീയമായി സ്വതന്ത്രമാണ്.

രേഖീയമായി ആശ്രിതമാണോ അതോ രേഖീയമായി സ്വതന്ത്രമാണോ എന്ന് വ്യക്തമാക്കാതെ വെക്റ്ററുകളുടെ ഒരു സിസ്റ്റം നമുക്ക് പരിഗണിക്കാം. കോളം വെക്റ്ററുകൾ അടങ്ങുന്ന ഓരോ സിസ്റ്റത്തിനും, സാധ്യമായ പരമാവധി രേഖീയ സ്വതന്ത്ര വെക്റ്ററുകൾ തിരിച്ചറിയാൻ കഴിയും. അക്ഷരത്താൽ സൂചിപ്പിക്കുന്ന ഈ സംഖ്യ ഈ വെക്റ്റർ സിസ്റ്റത്തിന്റെ റാങ്കാണ്. ഓരോ മാട്രിക്സും കോളം വെക്റ്ററുകളുടെ ഒരു സിസ്റ്റമായി കാണാൻ കഴിയുന്നതിനാൽ, ഒരു മാട്രിക്സിന്റെ റാങ്ക് അതിൽ അടങ്ങിയിരിക്കുന്ന പരമാവധി രേഖീയ സ്വതന്ത്ര കോളം വെക്റ്ററുകളായി നിർവചിക്കപ്പെടുന്നു. ഒരു മാട്രിക്സിന്റെ റാങ്ക് നിർണ്ണയിക്കാൻ റോ വെക്റ്ററുകളും ഉപയോഗിക്കുന്നു. രണ്ട് രീതികളും ഒരേ മാട്രിക്‌സിന് ഒരേ ഫലം നൽകുന്നു, കൂടാതെ 0 മുതൽ . വരെയുള്ള ക്രമത്തിലുള്ള ഒരു സ്‌ക്വയർ മാട്രിക്‌സിന്റെ ഏറ്റവും ചെറിയ അല്ലെങ്കിൽ റാങ്ക് കവിയരുത്. എല്ലാ വെക്റ്ററുകളും പൂജ്യമാണെങ്കിൽ, അത്തരമൊരു മാട്രിക്സിന്റെ റാങ്ക് പൂജ്യമാണ്. എല്ലാ വെക്റ്ററുകളും പരസ്പരം രേഖീയമായി സ്വതന്ത്രമാണെങ്കിൽ, മാട്രിക്സിന്റെ റാങ്ക് തുല്യമാണ്. മുകളിലുള്ള വെക്റ്ററുകളിൽ നിന്ന് ഒരു മാട്രിക്സ് ഉണ്ടാക്കുകയാണെങ്കിൽ, ഈ മെട്രിക്സിന്റെ റാങ്ക് 2 ആണ്. ഓരോ രണ്ട് വെക്റ്ററുകളും ഒരു ലീനിയർ കോമ്പിനേഷൻ വഴി മൂന്നിലൊന്നായി കുറയ്ക്കാൻ കഴിയുമെന്നതിനാൽ, റാങ്ക് 3-ൽ താഴെയാണ്.

എന്നാൽ അവയിൽ ഏതെങ്കിലും രണ്ട് വെക്‌ടറുകൾ രേഖീയമായി സ്വതന്ത്രമാണെന്ന് ഉറപ്പാക്കാൻ കഴിയും, അതിനാൽ റാങ്ക്

ഒരു സ്ക്വയർ മാട്രിക്സ് അതിന്റെ കോളം വെക്റ്ററുകൾ അല്ലെങ്കിൽ വരി വെക്റ്ററുകൾ രേഖീയമായി ആശ്രിതമാണെങ്കിൽ അതിനെ ഏകവചനം എന്ന് വിളിക്കുന്നു. അത്തരമൊരു മാട്രിക്സിന്റെ ഡിറ്റർമിനന്റ് പൂജ്യത്തിന് തുല്യമാണ്, മുകളിൽ സൂചിപ്പിച്ചതുപോലെ അതിന്റെ വിപരീത മാട്രിക്സ് നിലവിലില്ല. ഈ നിഗമനങ്ങൾ പരസ്പരം തുല്യമാണ്. തൽഫലമായി, ഒരു ചതുര മാട്രിക്‌സിനെ അതിന്റെ കോളം വെക്‌റ്ററുകളോ വരി വെക്‌റ്ററുകളോ പരസ്പരം സ്വതന്ത്രമാണെങ്കിൽ, അതിനെ ഏകമല്ലാത്ത അല്ലെങ്കിൽ ഏകവചനമല്ല എന്ന് വിളിക്കുന്നു. അത്തരമൊരു മാട്രിക്സിന്റെ ഡിറ്റർമിനന്റ് പൂജ്യത്തിന് തുല്യമല്ല, അതിന്റെ വിപരീത മാട്രിക്സ് നിലവിലുണ്ട് (പേജ് 43 മായി താരതമ്യം ചെയ്യുക)

മാട്രിക്സിന്റെ റാങ്കിന് വ്യക്തമായ ജ്യാമിതീയ വ്യാഖ്യാനമുണ്ട്. മാട്രിക്സിന്റെ റാങ്ക് തുല്യമാണെങ്കിൽ, -ഡൈമൻഷണൽ സ്പേസ് വെക്റ്ററുകളാൽ വ്യാപിച്ചതായി പറയപ്പെടുന്നു. റാങ്ക് ആണെങ്കിൽ വെക്‌ടറുകൾ എല്ലാം ഉൾപ്പെടുന്ന ഒരു -ഡൈമൻഷണൽ സബ്‌സ്‌പെയ്‌സിൽ കിടക്കുന്നു. അതിനാൽ, മാട്രിക്സിന്റെ റാങ്ക് "എല്ലാ വെക്റ്ററുകളും ഉൾക്കൊള്ളുന്ന" സ്ഥലത്തിന്റെ ആവശ്യമായ ഏറ്റവും കുറഞ്ഞ അളവുമായി യോജിക്കുന്നു; ഒരു -ഡൈമൻഷണൽ സ്പേസിലെ ഒരു -ഡൈമൻഷണൽ സബ്സ്പേസിനെ -ഡൈമൻഷണൽ ഹൈപ്പർപ്ലെയ്ൻ എന്ന് വിളിക്കുന്നു. മാട്രിക്സിന്റെ റാങ്ക് എല്ലാ വെക്റ്ററുകളും ഇപ്പോഴും കിടക്കുന്ന ഹൈപ്പർപ്ലെയിനിന്റെ ഏറ്റവും ചെറിയ അളവുമായി യോജിക്കുന്നു.

ഓർത്തോഗണാലിറ്റി. a, b എന്നീ രണ്ട് വെക്‌ടറുകൾ അവയുടെ സ്‌കെലാർ പ്രോഡക്‌ട് പൂജ്യമാണെങ്കിൽ അവ പരസ്പരം ഓർത്തോഗണൽ ആണെന്ന് പറയപ്പെടുന്നു. ഡി ഒരു ഡയഗണൽ മാട്രിക്‌സ് ആയിരിക്കുന്നിടത്ത് ഓർഡർ മാട്രിക്‌സിന് തുല്യതയുണ്ടെങ്കിൽ, മാട്രിക്‌സ് എയുടെ കോളം വെക്‌റ്ററുകൾ ജോടിയായി പരസ്പരം ഓർത്തോഗണലാണ്. ഈ നിര വെക്റ്ററുകൾ നോർമലൈസ് ചെയ്താൽ, അതായത്, 1 ന് തുല്യമായ ദൈർഘ്യത്തിലേക്ക് ചുരുക്കിയാൽ, സമത്വം സംഭവിക്കുന്നു, നമ്മൾ ഓർത്തോനോർമൽ വെക്റ്ററുകളെ കുറിച്ച് സംസാരിക്കുന്നു. B ഒരു ചതുര മാട്രിക്സ് ആണെങ്കിൽ, തുല്യത നിലനിൽക്കുകയാണെങ്കിൽ, മാട്രിക്സ് Bയെ ഓർത്തോഗണൽ എന്ന് വിളിക്കുന്നു. ഈ സാഹചര്യത്തിൽ, ഓർത്തോഗണൽ മാട്രിക്സ് എല്ലായ്പ്പോഴും ഏകവചനമല്ലെന്ന് ഫോർമുലയിൽ നിന്ന് (1.22) പിന്തുടരുന്നു. അതിനാൽ, മാട്രിക്സിന്റെ ഓർത്തോഗണാലിറ്റിയിൽ നിന്ന്, അതിന്റെ വരി വെക്റ്ററുകളുടെ അല്ലെങ്കിൽ നിര വെക്റ്ററുകളുടെ രേഖീയ സ്വാതന്ത്ര്യം പിന്തുടരുന്നു. വിപരീത പ്രസ്താവന ശരിയല്ല: വെക്റ്ററുകളുടെ ഒരു സിസ്റ്റത്തിന്റെ ലീനിയർ ഇൻഡിപെൻഡൻസ് ഈ വെക്റ്ററുകളുടെ പെയർവൈസ് ഓർത്തോഗണാലിറ്റിയെ സൂചിപ്പിക്കുന്നില്ല.

ചില സംഖ്യകൾ എവിടെയാണ് (ഈ സംഖ്യകളിൽ ചിലത് അല്ലെങ്കിൽ അവയെല്ലാം പൂജ്യത്തിന് തുല്യമായിരിക്കാം). നിരകളുടെ ഘടകങ്ങൾക്കിടയിൽ ഇനിപ്പറയുന്ന തുല്യതകൾ ഉണ്ടെന്നാണ് ഇതിനർത്ഥം:

(3.3.1) മുതൽ അത് പിന്തുടരുന്നു

സമത്വം (3.3.3) ആണെങ്കിൽ മാത്രം ശരിയാണെങ്കിൽ, വരികളെ രേഖീയമായി സ്വതന്ത്രമെന്ന് വിളിക്കുന്നു. റിലേഷൻ (3.3.2) കാണിക്കുന്നത് വരികളിലൊന്ന് മറ്റുള്ളവയുടെ അടിസ്ഥാനത്തിൽ രേഖീയമായി പ്രകടിപ്പിക്കുകയാണെങ്കിൽ, വരികൾ രേഖീയമായി ആശ്രയിച്ചിരിക്കുന്നു.

വിപരീതമായി കാണുന്നത് എളുപ്പമാണ്: സ്ട്രിംഗുകൾ രേഖീയമായി ആശ്രിതമാണെങ്കിൽ, ശേഷിക്കുന്ന സ്ട്രിംഗുകളുടെ രേഖീയ സംയോജനമായ ഒരു സ്ട്രിംഗ് ഉണ്ട്.

ഉദാഹരണത്തിന്, (3.3.3) ൽ അനുവദിക്കുക .

നിർവ്വചനം. മാട്രിക്സ് A-ൽ ഒരു നിശ്ചിത r-th ഓർഡർ മൈനർ തിരിച്ചറിയട്ടെ, അതേ മാട്രിക്സിന്റെ (r+1)-th ഓർഡർ മൈനറിൽ മൈനർ പൂർണ്ണമായും അടങ്ങിയിരിക്കട്ടെ. ഈ സാഹചര്യത്തിൽ മൈനർ മൈനറിന്റെ അതിർത്തിയാണെന്ന് ഞങ്ങൾ പറയും (അല്ലെങ്കിൽ ബോർഡറാണ്).

ഇപ്പോൾ ഞങ്ങൾ ഒരു പ്രധാന ലെമ്മ തെളിയിക്കും.

ലെമ്മപ്രായപൂർത്തിയാകാത്തവരെ കുറിച്ച്. മാട്രിക്സ് A= ന്റെ ഒരു മൈനർ ഓർഡർ r പൂജ്യത്തിൽ നിന്ന് വ്യത്യസ്തമാണെങ്കിൽ, അതിന്റെ അതിർത്തിയിലുള്ള എല്ലാ പ്രായപൂർത്തിയാകാത്തവരും പൂജ്യത്തിന് തുല്യമാണെങ്കിൽ, മാട്രിക്സ് A യുടെ ഏത് വരിയും (നിര) അതിന്റെ വരികളുടെ (നിരകളുടെ) രേഖീയ സംയോജനമാണ് .

തെളിവ്. ന്യായവാദത്തിന്റെ സാമാന്യത നഷ്‌ടപ്പെടാതെ, rth ക്രമത്തിന്റെ പൂജ്യമല്ലാത്ത ഒരു മൈനർ മാട്രിക്‌സ് A =:

.

മാട്രിക്സ് A യുടെ ആദ്യ k വരികൾക്ക്, ലെമ്മയുടെ പ്രസ്താവന വ്യക്തമാണ്: ഒരു രേഖീയ സംയോജനത്തിൽ ഒരേ വരി ഒന്നിന് തുല്യമായ ഒരു ഗുണകവും ബാക്കിയുള്ളവ - പൂജ്യത്തിന് തുല്യമായ ഗുണകങ്ങളും ഉൾപ്പെടുത്തിയാൽ മതി.

മാട്രിക്സ് A യുടെ ശേഷിക്കുന്ന വരികൾ ആദ്യ k വരികളിലൂടെ രേഖീയമായി പ്രകടിപ്പിക്കുന്നുവെന്ന് നമുക്ക് ഇപ്പോൾ തെളിയിക്കാം. ഇത് ചെയ്യുന്നതിന്, മൈനറിലേക്ക് kth ലൈൻ () ചേർത്ത് ഞങ്ങൾ (r+1) ക്രമത്തിന്റെ ഒരു മൈനർ നിർമ്മിക്കുന്നു. എൽമത്തെ കോളം():

.

തത്ഫലമായുണ്ടാകുന്ന മൈനർ എല്ലാ k, l എന്നിവയ്ക്കും പൂജ്യത്തിന് തുല്യമാണ്. എങ്കിൽ, രണ്ട് സമാന നിരകൾ അടങ്ങിയിരിക്കുന്നതിനാൽ അത് പൂജ്യത്തിന് തുല്യമാണ്. എങ്കിൽ, ഫലമായുണ്ടാകുന്ന മൈനർ ഒരു എഡ്ജ് മൈനറാണ്, അതിനാൽ, ലെമ്മയുടെ വ്യവസ്ഥകൾ പ്രകാരം പൂജ്യത്തിന് തുല്യമാണ്.

അവസാനത്തെ മൂലകങ്ങൾക്കനുസരിച്ച് മൈനറിനെ വിഘടിപ്പിക്കാം എൽമത്തെ കോളം:

ഊഹിച്ചാൽ, നമുക്ക് ലഭിക്കുന്നത്:

(3.3.6)

എക്സ്പ്രഷൻ (3.3.6) എന്നാൽ മാട്രിക്സ് A യുടെ kth വരി ആദ്യ r വരികളിലൂടെ രേഖീയമായി പ്രകടിപ്പിക്കുന്നു എന്നാണ്.

ഒരു മാട്രിക്സ് കൈമാറ്റം ചെയ്യുമ്പോൾ, അതിന്റെ പ്രായപൂർത്തിയാകാത്തവരുടെ മൂല്യങ്ങൾ മാറില്ല (ഡിറ്റർമിനന്റുകളുടെ സ്വത്ത് കാരണം), തുടർന്ന് തെളിയിക്കപ്പെട്ടതെല്ലാം നിരകൾക്കും ശരിയാണ്. സിദ്ധാന്തം തെളിയിക്കപ്പെട്ടു.

പരിണതഫലം I. ഒരു മാട്രിക്സിന്റെ ഏത് വരിയും (നിര) അതിന്റെ അടിസ്ഥാന വരികളുടെ (നിരകൾ) ഒരു രേഖീയ സംയോജനമാണ്. തീർച്ചയായും, മാട്രിക്സിന്റെ അടിസ്ഥാന മൈനർ പൂജ്യമല്ല, അതിന്റെ അതിർത്തിയിലുള്ള എല്ലാ പ്രായപൂർത്തിയാകാത്തവരും പൂജ്യത്തിന് തുല്യമാണ്.

ഫലം II. ഒരു nth ഓർഡർ ഡിറ്റർമിനന്റ് പൂജ്യത്തിന് തുല്യമാണ്, അതിൽ രേഖീയമായി ആശ്രിത വരികൾ (നിരകൾ) ഉണ്ടെങ്കിൽ മാത്രം. ഡിറ്റർമിനന്റ് പൂജ്യത്തിന് തുല്യമാകുന്നതിന് വരികളുടെ (നിരകൾ) രേഖീയ ആശ്രിതത്വത്തിന്റെ പര്യാപ്തത ഡിറ്റർമിനന്റുകളുടെ ഒരു സ്വത്തായി നേരത്തെ തെളിയിക്കപ്പെട്ടിരുന്നു.

ആവശ്യം തെളിയിക്കാം. മൈനർ പൂജ്യം മാത്രമുള്ള n-ആം ക്രമത്തിന്റെ ഒരു ചതുര മാട്രിക്സ് നമുക്ക് നൽകാം. ഈ മാട്രിക്സിന്റെ റാങ്ക് n-നേക്കാൾ കുറവാണ്, അതായത്. ഈ മാട്രിക്സിന്റെ അടിസ്ഥാന വരികളുടെ രേഖീയ സംയോജനമായ ഒരു വരിയെങ്കിലും ഉണ്ട്.

മാട്രിക്സിന്റെ റാങ്കിനെക്കുറിച്ചുള്ള മറ്റൊരു സിദ്ധാന്തം നമുക്ക് തെളിയിക്കാം.

സിദ്ധാന്തം.ഒരു മാട്രിക്സിന്റെ രേഖീയ സ്വതന്ത്ര വരികളുടെ പരമാവധി എണ്ണം അതിന്റെ രേഖീയ സ്വതന്ത്ര നിരകളുടെ പരമാവധി എണ്ണത്തിന് തുല്യവും ഈ മാട്രിക്സിന്റെ റാങ്കിന് തുല്യവുമാണ്.

തെളിവ്. മാട്രിക്സ് A= ന്റെ റാങ്ക് r ന് തുല്യമായിരിക്കട്ടെ. അപ്പോൾ അതിന്റെ k അടിസ്ഥാന വരികളിൽ ഏതെങ്കിലും രേഖീയമായി സ്വതന്ത്രമായിരിക്കും, അല്ലാത്തപക്ഷം അടിസ്ഥാന മൈനർ പൂജ്യത്തിന് തുല്യമായിരിക്കും. മറുവശത്ത്, ഏതെങ്കിലും r+1 അല്ലെങ്കിൽ അതിൽ കൂടുതൽ വരികൾ രേഖീയമായി ആശ്രയിച്ചിരിക്കുന്നു. നേരെമറിച്ച് അനുമാനിക്കുകയാണെങ്കിൽ, മുൻ ലെമ്മയുടെ കോറോളറി 2 പ്രകാരം പൂജ്യമല്ലാത്ത r-നേക്കാൾ വലിയ ക്രമത്തിന്റെ ഒരു മൈനർ നമുക്ക് കണ്ടെത്താനാകും. രണ്ടാമത്തേത് പൂജ്യമല്ലാത്ത പ്രായപൂർത്തിയാകാത്തവരുടെ പരമാവധി ക്രമം r ആണ് എന്ന വസ്തുതയ്ക്ക് വിരുദ്ധമാണ്. വരികൾക്കായി തെളിയിക്കപ്പെട്ടതെല്ലാം നിരകൾക്കും ശരിയാണ്.

ഉപസംഹാരമായി, ഒരു മാട്രിക്സിന്റെ റാങ്ക് കണ്ടെത്തുന്നതിനുള്ള മറ്റൊരു രീതി ഞങ്ങൾ രൂപപ്പെടുത്തും. പൂജ്യത്തിൽ നിന്ന് വ്യത്യസ്‌തമായ പരമാവധി ക്രമത്തിന്റെ ഒരു മൈനർ കണ്ടെത്തുന്നതിലൂടെ ഒരു മാട്രിക്‌സിന്റെ റാങ്ക് നിർണ്ണയിക്കാനാകും.

ഒറ്റനോട്ടത്തിൽ, ഇതിന് ഒരു പരിമിതമായ കണക്കുകൂട്ടൽ ആവശ്യമാണ്, പക്ഷേ ഈ മാട്രിക്സിന്റെ പ്രായപൂർത്തിയാകാത്തവരുടെ എണ്ണം വളരെ കൂടുതലായിരിക്കാം.

എന്നിരുന്നാലും, ഇതിൽ കാര്യമായ ലളിതവൽക്കരണങ്ങൾ അവതരിപ്പിക്കാൻ ഇനിപ്പറയുന്ന സിദ്ധാന്തം അനുവദിക്കുന്നു.

സിദ്ധാന്തം.മാട്രിക്സ് A-യുടെ മൈനർ പൂജ്യമല്ലെങ്കിൽ, അതിന്റെ അതിർത്തിയിലുള്ള എല്ലാ പ്രായപൂർത്തിയാകാത്തവരും പൂജ്യത്തിന് തുല്യമാണെങ്കിൽ, മാട്രിക്സിന്റെ റാങ്ക് r-ന് തുല്യമാണ്.

തെളിവ്. S>r-നുള്ള മാട്രിക്സ് വരികളുടെ ഏതെങ്കിലും ഉപസിസ്റ്റം സിദ്ധാന്തത്തിന്റെ വ്യവസ്ഥകൾക്ക് കീഴിൽ രേഖീയമായി ആശ്രയിക്കുമെന്ന് കാണിച്ചാൽ മതിയാകും (r എന്നത് ലീനിയർ ഇൻഡിപെൻഡന്റ് മാട്രിക്സ് വരികളുടെ പരമാവധി എണ്ണം അല്ലെങ്കിൽ അതിന്റെ ഏതെങ്കിലും മൈനർ ഓർഡർ k-നേക്കാൾ വലുതാണ്. പൂജ്യത്തിന് തുല്യമാണ്).

നമുക്ക് വിപരീതമായി അനുമാനിക്കാം. വരികൾ രേഖീയമായി സ്വതന്ത്രമായിരിക്കട്ടെ. ബോർഡർ ചെയ്യുന്ന പ്രായപൂർത്തിയാകാത്തവരെക്കുറിച്ചുള്ള ലെമ്മ പ്രകാരം, അവ ഓരോന്നും മൈനർ ഉൾക്കൊള്ളുന്ന വരികളുടെ അടിസ്ഥാനത്തിൽ രേഖീയമായി പ്രകടിപ്പിക്കും, അവ പൂജ്യമല്ലാത്തതിനാൽ രേഖീയമായി സ്വതന്ത്രമാണ്:

ഇപ്പോൾ ഇനിപ്പറയുന്ന രേഖീയ സംയോജനം പരിഗണിക്കുക:

അഥവാ

(3.3.7), (3.3.8) എന്നിവ ഉപയോഗിച്ച് നമുക്ക് ലഭിക്കും

,

ഇത് രേഖീയ വരി സ്വാതന്ത്ര്യത്തിന് വിരുദ്ധമാണ്.

തൽഫലമായി, ഞങ്ങളുടെ അനുമാനം തെറ്റാണ്, അതിനാൽ, സിദ്ധാന്തത്തിന്റെ വ്യവസ്ഥകൾക്ക് കീഴിലുള്ള ഏതെങ്കിലും S>r വരികൾ രേഖീയമായി ആശ്രയിച്ചിരിക്കുന്നു. സിദ്ധാന്തം തെളിയിക്കപ്പെട്ടു.

ഈ സിദ്ധാന്തത്തെ അടിസ്ഥാനമാക്കി, ഒരു മാട്രിക്സിന്റെ റാങ്ക് കണക്കാക്കുന്നതിനുള്ള നിയമം നമുക്ക് പരിഗണിക്കാം - പ്രായപൂർത്തിയാകാത്തവരെ അതിർത്തിയാക്കുന്നതിനുള്ള രീതി.

ഒരു മാട്രിക്സിന്റെ റാങ്ക് കണക്കാക്കുമ്പോൾ, താഴ്ന്ന ഓർഡറുകളുടെ പ്രായപൂർത്തിയാകാത്തവരിൽ നിന്ന് ഉയർന്ന ഓർഡറുകളുടെ പ്രായപൂർത്തിയാകാത്തവരിലേക്ക് മാറണം. പൂജ്യത്തിൽ നിന്ന് വ്യത്യസ്‌തമായ rth ഓർഡറിന്റെ ഒരു മൈനർ ഇതിനകം കണ്ടെത്തിയിട്ടുണ്ടെങ്കിൽ, മൈനറിന്റെ അതിർത്തിയിലുള്ള (r+1)മത്തെ ഓർഡറിന്റെ മൈനറുകൾ മാത്രം കണക്കാക്കേണ്ടത് ആവശ്യമാണ്. അവ പൂജ്യത്തിന് തുല്യമാണെങ്കിൽ, മാട്രിക്സിന്റെ റാങ്ക് r ന് തുല്യമാണ്. ഞങ്ങൾ മെട്രിക്സിന്റെ റാങ്ക് കണക്കാക്കുക മാത്രമല്ല, മെട്രിക്സിന്റെ അടിസ്ഥാന മൈനർ ഏത് നിരകൾ (വരികൾ) നിർമ്മിക്കുന്നുവെന്ന് നിർണ്ണയിക്കുകയും ചെയ്താൽ ഈ രീതിയും ഉപയോഗിക്കുന്നു.

ഉദാഹരണം. ബോർഡറിംഗ് മൈനേഴ്സ് രീതി ഉപയോഗിച്ച് മാട്രിക്സിന്റെ റാങ്ക് കണക്കാക്കുക

.

പരിഹാരം. മാട്രിക്സ് എയുടെ മുകളിൽ ഇടത് കോണിൽ സ്ഥിതി ചെയ്യുന്ന രണ്ടാമത്തെ ഓർഡർ മൈനർ പൂജ്യമല്ല:

.

എന്നിരുന്നാലും, അതിനെ ചുറ്റിപ്പറ്റിയുള്ള എല്ലാ മൂന്നാം-നിര പ്രായപൂർത്തിയാകാത്തവരും പൂജ്യത്തിന് തുല്യമാണ്:

;	;
;	;
;	.

അതിനാൽ, മാട്രിക്സ് എയുടെ റാങ്ക് രണ്ടിന് തുല്യമാണ്: .

ഒന്നാമത്തെയും രണ്ടാമത്തെയും വരികൾ, ഈ മാട്രിക്സിലെ ഒന്നും രണ്ടും നിരകൾ അടിസ്ഥാനപരമാണ്. ശേഷിക്കുന്ന വരികളും നിരകളും അവയുടെ രേഖീയ സംയോജനമാണ്. വാസ്തവത്തിൽ, താഴെപ്പറയുന്ന തുല്യതകൾ സ്ട്രിംഗുകൾക്കായി നിലനിർത്തുന്നു:

ഉപസംഹാരമായി, ഇനിപ്പറയുന്ന ഗുണങ്ങളുടെ സാധുത ഞങ്ങൾ ശ്രദ്ധിക്കുന്നു:

1) മെട്രിക്സുകളുടെ ഉൽപ്പന്നത്തിന്റെ റാങ്ക് ഓരോ ഘടകങ്ങളുടെയും റാങ്കിനേക്കാൾ വലുതല്ല;

2) അനിയന്ത്രിതമായ മാട്രിക്സ് A യുടെ ഗുണനത്തിന്റെ റാങ്ക് വലത്തോട്ടും ഇടത്തോട്ടും ഒരു ഏകവചനമല്ലാത്ത ചതുര മാട്രിക്സ് Q എന്നത് മാട്രിക്സ് A യുടെ റാങ്കിന് തുല്യമാണ്.

പോളിനോമിയൽ മെട്രിക്സ്

നിർവ്വചനം. ഒരു പോളിനോമിയൽ മാട്രിക്സ് അല്ലെങ്കിൽ -മാട്രിക്സ് എന്നത് ഒരു ചതുരാകൃതിയിലുള്ള മാട്രിക്സാണ്, അതിന്റെ ഘടകങ്ങൾ സംഖ്യാ ഗുണകങ്ങളുള്ള ഒരു വേരിയബിളിലെ പോളിനോമിയലുകളാണ്.

പ്രാഥമിക പരിവർത്തനങ്ങൾ -മെട്രിക്സിൽ നടത്താം. ഇതിൽ ഉൾപ്പെടുന്നവ:

രണ്ട് വരികൾ (നിരകൾ) പുനഃക്രമീകരിക്കുന്നു;

പൂജ്യം അല്ലാതെ മറ്റൊരു സംഖ്യ കൊണ്ട് ഒരു വരി (നിര) ഗുണിക്കുക;

ഒരു വരിയിലേക്ക് (നിര) മറ്റൊരു വരി (നിര) ചേർക്കുന്നത് ഏതെങ്കിലും ബഹുപദത്താൽ ഗുണിച്ചാൽ.

രണ്ട് -മെട്രിക്സുകളും ഒരേ വലിപ്പവും തുല്യമാണെന്ന് പറയപ്പെടുന്നു: , ഒരാൾക്ക് മാട്രിക്സിൽ നിന്ന് പരിമിതമായ എലിമെന്ററി പരിവർത്തനങ്ങൾ ഉപയോഗിക്കാനാകുമെങ്കിൽ.

ഉദാഹരണം. മാട്രിക്സ് തുല്യത തെളിയിക്കുക

,

.

1. മാട്രിക്സിലെ ഒന്നും രണ്ടും നിരകൾ സ്വാപ്പ് ചെയ്യുക:

.

2. രണ്ടാമത്തെ വരിയിൽ നിന്ന്, ആദ്യത്തേത് കുറയ്ക്കുക, ഗുണിച്ച് ():

.

3. രണ്ടാമത്തെ വരിയെ (–1) കൊണ്ട് ഗുണിക്കുക, അത് ശ്രദ്ധിക്കുക

.

4. രണ്ടാമത്തെ നിരയിൽ നിന്ന് ആദ്യത്തേത് കുറയ്ക്കുക, ഗുണിച്ചാൽ നമുക്ക് ലഭിക്കും

.

നൽകിയിരിക്കുന്ന വലുപ്പത്തിലുള്ള എല്ലാ മെട്രിക്സുകളുടെയും സെറ്റ് തുല്യമായ മെട്രിക്സുകളുടെ വിഭജന ക്ലാസുകളായി തിരിച്ചിരിക്കുന്നു. പരസ്പരം തുല്യമായ മെട്രിസുകൾ ഒരു ക്ലാസും തുല്യമല്ലാത്തവ മറ്റൊരു വർഗ്ഗവും ഉണ്ടാക്കുന്നു.

തത്തുല്യമായ മെട്രിക്സുകളുടെ ഓരോ ക്ലാസും നൽകിയിരിക്കുന്ന അളവുകളുടെ ഒരു കാനോനിക്കൽ അല്ലെങ്കിൽ സാധാരണ മാട്രിക്സാണ്.

നിർവ്വചനം. കാനോനിക്കൽ, അല്ലെങ്കിൽ സാധാരണ, അളവുകളുടെ മാട്രിക്സ് ഒരു മാട്രിക്സ് ആണ്, അതിന്റെ പ്രധാന ഡയഗണലിൽ ബഹുപദങ്ങൾ അടങ്ങിയിരിക്കുന്നു, ഇവിടെ p എന്നത് m, n എന്നീ സംഖ്യകളുടെ ചെറുതാണ് ( ), പൂജ്യത്തിന് തുല്യമല്ലാത്ത പോളിനോമിയലുകൾക്ക് ലീഡിംഗ് ഗുണകങ്ങൾ 1 ന് തുല്യമാണ്, കൂടാതെ തുടർന്നുള്ള ഓരോ പോളിനോമിയലും മുമ്പത്തേത് കൊണ്ട് ഹരിക്കുന്നു. പ്രധാന ഡയഗണലിന് പുറത്തുള്ള എല്ലാ ഘടകങ്ങളും 0 ആണ്.

പോളിനോമിയലുകൾക്കിടയിൽ ഡിഗ്രി പൂജ്യത്തിന്റെ പോളിനോമിയലുകൾ ഉണ്ടെങ്കിൽ, അവ പ്രധാന ഡയഗണലിന്റെ തുടക്കത്തിലാണെന്ന് നിർവചനം പിന്തുടരുന്നു. പൂജ്യങ്ങൾ ഉണ്ടെങ്കിൽ, അവ പ്രധാന ഡയഗണലിന്റെ അവസാനത്തിലാണ്.

മുമ്പത്തെ ഉദാഹരണത്തിന്റെ മാട്രിക്സ് കാനോനിക്കൽ ആണ്. മാട്രിക്സ്

കാനോനികവും.

-മെട്രിക്സിന്റെ ഓരോ ക്ലാസിലും ഒരു അദ്വിതീയ കാനോനിക്കൽ -മാട്രിക്സ് അടങ്ങിയിരിക്കുന്നു, അതായത്. ഓരോ -മാട്രിക്സും ഒരു അദ്വിതീയ കാനോനിക്കൽ മാട്രിക്സിന് തുല്യമാണ്, അതിനെ കാനോനിക്കൽ ഫോം അല്ലെങ്കിൽ ആ മാട്രിക്സിന്റെ സാധാരണ രൂപം എന്ന് വിളിക്കുന്നു.

തന്നിരിക്കുന്ന -മാട്രിക്സിന്റെ കാനോനിക്കൽ രൂപത്തിന്റെ പ്രധാന ഡയഗണലിൽ സ്ഥിതിചെയ്യുന്ന ബഹുപദങ്ങളെ ഈ മാട്രിക്സിന്റെ മാറ്റമില്ലാത്ത ഘടകങ്ങൾ എന്ന് വിളിക്കുന്നു.

മാറ്റമില്ലാത്ത ഘടകങ്ങൾ കണക്കാക്കുന്നതിനുള്ള ഒരു രീതി, തന്നിരിക്കുന്ന -മാട്രിക്സിനെ കാനോനിക്കൽ രൂപത്തിലേക്ക് കുറയ്ക്കുക എന്നതാണ്.

അതിനാൽ, മുമ്പത്തെ ഉദാഹരണത്തിന്റെ മാട്രിക്സിന്, മാറ്റമില്ലാത്ത ഘടകങ്ങൾ

, , , .

മേൽപ്പറഞ്ഞതിൽ നിന്ന്, ഒരേ കൂട്ടം മാറ്റമില്ലാത്ത ഘടകങ്ങളുടെ സാന്നിധ്യം -മെട്രിക്സുകളുടെ തുല്യതയ്ക്ക് ആവശ്യമായതും മതിയായതുമായ ഒരു വ്യവസ്ഥയാണ്.

കാനോനിക്കൽ രൂപത്തിലേക്ക് -മാട്രിക്സ് കുറയ്ക്കുന്നത് മാറ്റമില്ലാത്ത ഘടകങ്ങൾ നിർണ്ണയിക്കുന്നതിലേക്ക് ചുരുക്കുന്നു

, ; ,

ഇവിടെ r എന്നത് മാട്രിക്സിന്റെ റാങ്കാണ്; - kth ഓർഡർ മൈനറുകളുടെ ഏറ്റവും വലിയ പൊതു വിഭജനം, ലീഡിംഗ് കോഫിഫിഷ്യന്റ് 1 ന് തുല്യമാണ്.

ഉദാഹരണം. നൽകട്ടെ -മാട്രിക്സ്

.

പരിഹാരം. വ്യക്തമായും, ആദ്യ ക്രമത്തിന്റെ ഏറ്റവും വലിയ പൊതു വിഭജനം, അതായത്. .

നമുക്ക് രണ്ടാം ഓർഡർ പ്രായപൂർത്തിയാകാത്തവരെ നിർവചിക്കാം:

,

തുടങ്ങിയവ.

ഒരു നിഗമനത്തിലെത്താൻ ഇതിനകം തന്നെ ഈ ഡാറ്റ മതിയാകും: അതിനാൽ, .

ഞങ്ങൾ നിർവചിക്കുന്നു

,

അതിനാൽ, .

അതിനാൽ, ഈ മാട്രിക്സിന്റെ കാനോനിക്കൽ രൂപം ഇനിപ്പറയുന്ന -മാട്രിക്സ് ആണ്:

.

ഒരു മാട്രിക്സ് പോളിനോമിയൽ രൂപത്തിന്റെ ഒരു ആവിഷ്കാരമാണ്

വേരിയബിൾ എവിടെയാണ്; - സംഖ്യാ ഘടകങ്ങളുള്ള n എന്ന ക്രമത്തിന്റെ ചതുര മെട്രിക്സ്.

എങ്കിൽ, S നെ മാട്രിക്സ് പോളിനോമിയലിന്റെ ഡിഗ്രി എന്ന് വിളിക്കുന്നു, n എന്നത് മാട്രിക്സ് പോളിനോമിയലിന്റെ ക്രമമാണ്.

ഏത് ക്വാഡ്രാറ്റിക് -മാട്രിക്സിനെയും മാട്രിക്സ് പോളിനോമിയൽ ആയി പ്രതിനിധീകരിക്കാം. വ്യക്തമായും, വിപരീത പ്രസ്താവനയും ശരിയാണ്, അതായത്. ഏതെങ്കിലും മാട്രിക്സ് പോളിനോമിയലിനെ ഒരു ചതുര മാട്രിക്സ് ആയി പ്രതിനിധീകരിക്കാം.

ഈ പ്രസ്താവനകളുടെ സാധുത മെട്രിക്സുകളിലെ പ്രവർത്തനങ്ങളുടെ സവിശേഷതകളിൽ നിന്ന് വ്യക്തമായി പിന്തുടരുന്നു. ഇനിപ്പറയുന്ന ഉദാഹരണങ്ങൾ നോക്കാം:

ഉദാഹരണം. ഒരു പോളിനോമിയൽ മാട്രിക്‌സിനെ പ്രതിനിധീകരിക്കുക

ഒരു മാട്രിക്സ് പോളിനോമിയലിന്റെ രൂപത്തിൽ താഴെ പറയുന്നു

.

ഉദാഹരണം. മാട്രിക്സ് ബഹുപദം

ഇനിപ്പറയുന്ന ബഹുപദ മാട്രിക്സ് (-മാട്രിക്സ്) ആയി പ്രതിനിധീകരിക്കാം

.

ഫാക്ടർ, ഘടക വിശകലന രീതികളുടെ ഗണിത ഉപകരണത്തിൽ മാട്രിക്സ് പോളിനോമിയലുകളുടെയും പോളിനോമിയൽ മെട്രിക്സുകളുടെയും ഈ പരസ്പര കൈമാറ്റം ഒരു പ്രധാന പങ്ക് വഹിക്കുന്നു.

സംഖ്യാ ഗുണകങ്ങളുള്ള സാധാരണ പോളിനോമിയലുകൾ പോലെ ഒരേ ക്രമത്തിലുള്ള മാട്രിക്സ് പോളിനോമിയലുകൾ കൂട്ടിച്ചേർക്കാനും കുറയ്ക്കാനും ഗുണിക്കാനും കഴിയും. എന്നിരുന്നാലും, മാട്രിക്സ് പോളിനോമിയലുകളുടെ ഗുണനം, പൊതുവായി പറഞ്ഞാൽ, കമ്മ്യൂട്ടേറ്റീവ് അല്ല, കാരണം മാട്രിക്സ് ഗുണനം കമ്മ്യൂട്ടേറ്റീവ് അല്ല.

രണ്ട് മാട്രിക്സ് പോളിനോമിയലുകൾ അവയുടെ ഗുണകങ്ങൾ തുല്യമാണെങ്കിൽ തുല്യമാണെന്ന് പറയപ്പെടുന്നു, അതായത്. വേരിയബിളിന്റെ അതേ ശക്തികൾക്കുള്ള അനുബന്ധ മെട്രിക്സ്.

രണ്ട് മാട്രിക്സ് പോളിനോമിയലുകളുടെ ആകെത്തുക (വ്യത്യാസം) ഒരു മാട്രിക്സ് പോളിനോമിയലാണ്, വേരിയബിളിന്റെ ഓരോ ഡിഗ്രിയുടെയും ഗുണകം പോളിനോമിയലുകളിലെ അതേ ഡിഗ്രിയിലെ ഗുണകങ്ങളുടെ ആകെത്തുക (വ്യത്യാസം) തുല്യമാണ്.

ഒരു മാട്രിക്സ് പോളിനോമിയലിനെ ഒരു മാട്രിക്സ് പോളിനോമിയൽ കൊണ്ട് ഗുണിക്കാൻ, നിങ്ങൾ മാട്രിക്സ് പോളിനോമിയലിന്റെ ഓരോ പദത്തെയും മാട്രിക്സ് പോളിനോമിയലിന്റെ ഓരോ പദവും കൊണ്ട് ഗുണിക്കേണ്ടതുണ്ട്, തത്ഫലമായുണ്ടാകുന്ന ഉൽപ്പന്നങ്ങൾ ചേർത്ത് സമാന പദങ്ങൾ കൊണ്ടുവരണം.

ഘടകങ്ങളുടെ ഡിഗ്രികളുടെ ആകെത്തുകയേക്കാൾ കുറവോ തുല്യമോ ആയ ഒരു ഉൽപ്പന്നമാണ് മാട്രിക്സ് പോളിനോമിയലിന്റെ ബിരുദം.

മാട്രിക്സ് പോളിനോമിയലുകളിലെ പ്രവർത്തനങ്ങൾ അനുബന്ധ -മെട്രിക്സുകളിലെ പ്രവർത്തനങ്ങൾ ഉപയോഗിച്ച് നടത്താം.

മാട്രിക്സ് പോളിനോമിയലുകൾ ചേർക്കാൻ (കുറയ്ക്കാൻ), അനുബന്ധ -മെട്രിക്സുകൾ ചേർത്താൽ മതിയാകും. ഗുണനത്തിനും ഇത് ബാധകമാണ്. മാട്രിക്സ് പോളിനോമിയലുകളുടെ ഗുണനത്തിന്റെ -മാട്രിക്സ് ഘടകങ്ങളുടെ -മെട്രിക്സിന്റെ ഗുണനത്തിന് തുല്യമാണ്.

മറുവശത്ത്, കൂടാതെ ഫോമിൽ എഴുതാം

ഇവിടെ B 0 എന്നത് ഏകമല്ലാത്ത ഒരു മാട്രിക്‌സ് ആണ്.

ഹരിക്കുമ്പോൾ ഒരു അദ്വിതീയ വലത് ഘടകവും വലത് ശേഷിപ്പും ഉണ്ടാകും

R 1 ന്റെ ബിരുദം ഡിഗ്രിയേക്കാൾ കുറവാണെങ്കിൽ , അല്ലെങ്കിൽ (ബാക്കി ഇല്ലാത്ത വിഭജനം), അതുപോലെ ഇടത് ഘടകവും ഇടത് ശേഷിയും എങ്കിൽ ക്രമമുണ്ടെങ്കിൽ മാത്രം

mxn വലുപ്പമുള്ള ഒരു ഏകപക്ഷീയമായ, ചതുരം ആയിരിക്കണമെന്നില്ല, മാട്രിക്സ് A പരിഗണിക്കുക.

മാട്രിക്സ് റാങ്ക്.

മാട്രിക്സ് റാങ്ക് എന്ന ആശയം മാട്രിക്സിന്റെ വരികളുടെ (നിരകൾ) ലീനിയർ ആശ്രിതത്വം (സ്വാതന്ത്ര്യം) എന്ന ആശയവുമായി ബന്ധപ്പെട്ടിരിക്കുന്നു. സ്ട്രിംഗുകൾക്കായി ഈ ആശയം പരിഗണിക്കാം. നിരകൾക്ക് - സമാനമായി.

മാട്രിക്സ് എയുടെ ഡ്രെയിനുകളെ നമുക്ക് സൂചിപ്പിക്കാം:

e 1 =(a 11,a 12,...,a 1n); e 2 =(a 21,a 22,...,a 2n);..., e m =(a m1,a m2,...,a mn)

ഒരു kj =a sj, j=1,2,…,n ആണെങ്കിൽ e k =e s

മാട്രിക്സ് വരികളിലെ ഗണിത പ്രവർത്തനങ്ങൾ (സങ്കലനം, ഒരു സംഖ്യ കൊണ്ട് ഗുണനം) മൂലകത്തിന്റെ മൂലകത്തിന്റെ പ്രവർത്തനങ്ങളായി അവതരിപ്പിക്കുന്നു: λе k =(λа k1 ,λа k2 ,…,λа kn);

e k +е s =[(a k1 +a s1),(a k2 +a s2),…,(a kn +a sn)].

ലൈൻ ഇ വിളിക്കുന്നു രേഖീയ സംയോജനംവരികൾ e 1, e 2,..., e k, ഇത് ഈ വരികളുടെ ഉൽപ്പന്നങ്ങളുടെ ആകെത്തുക അനിയന്ത്രിതമായ യഥാർത്ഥ സംഖ്യകളാൽ തുല്യമാണെങ്കിൽ:

e=λ 1 e 1 +λ 2 e 2 +…+λ k e k

e 1, e 2,..., e m എന്ന വരികളെ വിളിക്കുന്നു രേഖീയമായി ആശ്രയിക്കുന്നത്, യഥാർത്ഥ സംഖ്യകൾ ഉണ്ടെങ്കിൽ λ 1 ,λ 2 ,...,λ m , എല്ലാം പൂജ്യത്തിന് തുല്യമല്ല, ഈ സ്ട്രിംഗുകളുടെ രേഖീയ സംയോജനം പൂജ്യം സ്ട്രിംഗിന് തുല്യമാണ്: λ 1 e 1 +λ 2 e 2 +...+λ m e m = 0 ,എവിടെ 0 =(0,0,…,0) (1)

ഒരു രേഖീയ സംയോജനം പൂജ്യത്തിന് തുല്യമാണെങ്കിൽ, എല്ലാ ഗുണകങ്ങളും λ i പൂജ്യത്തിന് തുല്യമാണെങ്കിൽ മാത്രം (λ 1 =λ 2 =...=λ m =0), തുടർന്ന് വരികൾ e 1, e 2,..., e m എന്ന് വിളിക്കപ്പെടുന്നു രേഖീയമായി സ്വതന്ത്രമായ.

സിദ്ധാന്തം 1. e 1 , e 2 ,..., e m രേഖീയമായി ആശ്രിതമാകുന്നതിന്, ഈ സ്ട്രിംഗുകളിലൊന്ന് ശേഷിക്കുന്ന സ്ട്രിംഗുകളുടെ രേഖീയ സംയോജനമായിരിക്കേണ്ടത് ആവശ്യവും മതിയായതുമാണ്.

തെളിവ്. ആവശ്യം. e 1, e 2,..., e m സ്ട്രിംഗുകൾ രേഖീയമായി ആശ്രയിക്കട്ടെ. ഉറപ്പിക്കട്ടെ, (1) λ m ≠0, പിന്നെ

അത്. e m എന്നത് ശേഷിക്കുന്ന സ്ട്രിംഗുകളുടെ ഒരു രേഖീയ സംയോജനമാണ്. തുടങ്ങിയവ.

പര്യാപ്തത. സ്ട്രിംഗുകളിലൊന്ന്, ഉദാഹരണത്തിന് e m, ശേഷിക്കുന്ന സ്ട്രിംഗുകളുടെ ഒരു രേഖീയ സംയോജനമായിരിക്കട്ടെ. അപ്പോൾ സമത്വം നിലനിർത്തുന്ന സംഖ്യകൾ ഉണ്ടാകും, അത് രൂപത്തിൽ മാറ്റിയെഴുതാം

ഇവിടെ കുറഞ്ഞത് 1 ഗുണകങ്ങൾ, (-1), പൂജ്യത്തിന് തുല്യമല്ല. ആ. വരികൾ രേഖീയമായി ആശ്രയിച്ചിരിക്കുന്നു. തുടങ്ങിയവ.

നിർവ്വചനം. മൈനർ kth ഓർഡർ mxn വലിപ്പമുള്ള മാട്രിക്‌സ് എയെ k-th ഓർഡർ ഡിറ്റർമിനന്റ് എന്ന് വിളിക്കുന്നു, ഏതെങ്കിലും k വരികളുടെയും മാട്രിക്സ് A. (k≤min(m,n)) യുടെ ഏതെങ്കിലും k നിരകളുടെയും കവലയിൽ കിടക്കുന്ന മൂലകങ്ങൾ. .

ഉദാഹരണം., 1st ഓർഡർ പ്രായപൂർത്തിയാകാത്തവർ: =, =;

2nd ഓർഡർ പ്രായപൂർത്തിയാകാത്തവർ: , 3rd ഓർഡർ

ഒരു മൂന്നാം ഓർഡർ മാട്രിക്സിൽ 9 1st ഓർഡർ മൈനറുകളും 9 2nd ഓർഡർ മൈനറുകളും 1 3rd ഓർഡർ മൈനറും (ഈ മാട്രിക്സിന്റെ ഡിറ്റർമിനന്റ്) ഉണ്ട്.

നിർവ്വചനം. മാട്രിക്സ് എ റാങ്ക്ഈ മാട്രിക്സിന്റെ പൂജ്യമല്ലാത്ത മൈനറുകളുടെ ഏറ്റവും ഉയർന്ന ക്രമം. പദവി - rg A അല്ലെങ്കിൽ r(A).

മാട്രിക്സ് റാങ്ക് പ്രോപ്പർട്ടികൾ.

1) മാട്രിക്സ് A nxm ന്റെ റാങ്ക് അതിന്റെ ചെറിയ അളവുകളിൽ കവിയരുത്, അതായത്.

r(A)≤min(m,n).

2) എല്ലാ മാട്രിക്സ് ഘടകങ്ങളും 0 ന് തുല്യമാകുമ്പോൾ r (A)=0, അതായത്. A=0.

3) n-ആം ക്രമം r(A)=n ന്റെ ഒരു ചതുര മാട്രിക്സ് A ന്, A ഡീജനറേറ്റ് അല്ലാത്തപ്പോൾ.

(ഒരു ഡയഗണൽ മാട്രിക്സിന്റെ റാങ്ക് അതിന്റെ പൂജ്യമല്ലാത്ത ഡയഗണൽ മൂലകങ്ങളുടെ എണ്ണത്തിന് തുല്യമാണ്).

4) ഒരു മാട്രിക്സിന്റെ റാങ്ക് r ന് തുല്യമാണെങ്കിൽ, മാട്രിക്സിന് പൂജ്യത്തിന് തുല്യമല്ലാത്ത r എന്ന ക്രമത്തിന്റെ ഒരു മൈനർ എങ്കിലും ഉണ്ടായിരിക്കും, കൂടാതെ ഉയർന്ന ഓർഡറുകളിലെ എല്ലാ പ്രായപൂർത്തിയാകാത്തവരും പൂജ്യത്തിന് തുല്യമാണ്.

മാട്രിക്സിന്റെ റാങ്കുകൾക്ക് ഇനിപ്പറയുന്ന ബന്ധങ്ങൾ ഉണ്ട്:

2) r (A+B)≤r(A)+r(B); 3) r(AB)≤min(r(A),r(B));

3) r(A+B)≥│r(A)-r(B)│; 4) r (A T A)=r (A);

5) r(AB)=r(A), B എന്നത് ഒരു ചതുരം അല്ലാത്ത മാട്രിക്സ് ആണെങ്കിൽ.

6) r(AB)≥r(A)+r(B)-n, ഇവിടെ n എന്നത് മാട്രിക്സ് A യുടെ നിരകളുടെയോ B മാട്രിക്സ് വരികളുടെയോ എണ്ണമാണ്.

നിർവ്വചനം. r(A) എന്ന ക്രമത്തിന്റെ പൂജ്യമല്ലാത്ത മൈനറിനെ വിളിക്കുന്നു അടിസ്ഥാന മൈനർ. (മാട്രിക്സ് എയ്ക്ക് നിരവധി അടിസ്ഥാന പ്രായപൂർത്തിയാകാത്തവർ ഉണ്ടായിരിക്കാം). അടിസ്ഥാന മൈനർ ഉള്ള കവലയിലെ വരികളും നിരകളും യഥാക്രമം വിളിക്കുന്നു അടിസ്ഥാന ചരടുകൾഒപ്പം അടിസ്ഥാന നിരകൾ.

സിദ്ധാന്തം 2 (അടിസ്ഥാന മൈനറിനെ കുറിച്ച്).അടിസ്ഥാന വരികൾ (നിരകൾ) രേഖീയമായി സ്വതന്ത്രമാണ്. മാട്രിക്സ് A യുടെ ഏത് വരിയും (ഏതെങ്കിലും കോളം) അടിസ്ഥാന വരികളുടെ (നിരകൾ) ഒരു രേഖീയ സംയോജനമാണ്.

തെളിവ്. (സ്ട്രിംഗുകൾക്ക്). അടിസ്ഥാന വരികൾ രേഖീയമായി ആശ്രിതമാണെങ്കിൽ, സിദ്ധാന്തമനുസരിച്ച് (1) ഈ വരികളിലൊന്ന് മറ്റ് അടിസ്ഥാന വരികളുടെ രേഖീയ സംയോജനമായിരിക്കും, തുടർന്ന്, അടിസ്ഥാന മൈനറിന്റെ മൂല്യം മാറ്റാതെ, നിങ്ങൾക്ക് ഈ വരിയിൽ നിന്ന് സൂചിപ്പിച്ച രേഖീയ സംയോജനം കുറയ്ക്കാം. കൂടാതെ പൂജ്യം വരി നേടുക, അടിസ്ഥാന മൈനർ പൂജ്യത്തിൽ നിന്ന് വ്യത്യസ്തമാണ് എന്ന വസ്തുതയ്ക്ക് ഇത് വിരുദ്ധമാണ്. അത്. അടിസ്ഥാന വരികൾ രേഖീയമായി സ്വതന്ത്രമാണ്.

മാട്രിക്സ് A യുടെ ഏതെങ്കിലും വരി അടിസ്ഥാന വരികളുടെ രേഖീയ സംയോജനമാണെന്ന് നമുക്ക് തെളിയിക്കാം. കാരണം വരികളുടെ (നിരകൾ) ഏകപക്ഷീയമായ മാറ്റങ്ങളോടെ, ഡിറ്റർമിനന്റ് പൂജ്യത്തിന് തുല്യമായ സ്വത്ത് നിലനിർത്തുന്നു, തുടർന്ന്, സാമാന്യത നഷ്ടപ്പെടാതെ, അടിസ്ഥാന മൈനർ മാട്രിക്സിന്റെ മുകളിൽ ഇടത് കോണിലാണെന്ന് നമുക്ക് അനുമാനിക്കാം.

എ=,ആ. ആദ്യ r വരികളിലും ആദ്യ r നിരകളിലും സ്ഥിതി ചെയ്യുന്നു. 1£j£n, 1£i£m. (r+1) ക്രമത്തിന്റെ ഡിറ്റർമിനന്റ് എന്ന് നമുക്ക് കാണിക്കാം

j£r അല്ലെങ്കിൽ i£r ആണെങ്കിൽ, ഈ ഡിറ്റർമിനന്റ് പൂജ്യത്തിന് തുല്യമാണ്, കാരണം അതിന് സമാനമായ രണ്ട് നിരകളോ രണ്ട് സമാന വരികളോ ഉണ്ടായിരിക്കും.

j>r ഉം i>r ഉം ആണെങ്കിൽ, ഈ ഡിറ്റർമിനന്റ് മാട്രിക്സ് A യുടെ (r+1)ആം ക്രമത്തിന്റെ മൈനറാണ്. മുതൽ മാട്രിക്സിന്റെ റാങ്ക് r ആണ്, അതായത് ഉയർന്ന ഓർഡറിലെ ഏതെങ്കിലും മൈനർ 0 ന് തുല്യമാണ്.

അവസാന (ചേർത്ത) നിരയുടെ ഘടകങ്ങൾ അനുസരിച്ച് ഇത് വിപുലീകരിക്കുന്നു, നമുക്ക് ലഭിക്കും

a 1j A 1j +a 2j A 2j +...+a rj A rj +a ij A ij =0, ഇവിടെ അവസാന ബീജഗണിത പൂരകം A ij അടിസ്ഥാന മൈനർ M r മായി യോജിക്കുന്നു, അതിനാൽ A ij = M r ≠0.

അവസാനത്തെ സമത്വത്തെ A ij കൊണ്ട് ഹരിച്ചാൽ, a ij എന്ന മൂലകത്തെ നമുക്ക് ഒരു രേഖീയ സംയോജനമായി പ്രകടിപ്പിക്കാം: , എവിടെ .

നമുക്ക് i (i>r) യുടെ മൂല്യം നിശ്ചയിക്കാം, കൂടാതെ ഏതെങ്കിലും j (j=1,2,...,n) i-th വരിയിലെ ഘടകങ്ങൾ e i വരികളുടെ മൂലകങ്ങളിലൂടെ രേഖീയമായി പ്രകടിപ്പിക്കുന്നത് കണ്ടെത്താം. 1, e 2,...,e r, അതായത് e. i-th വരി അടിസ്ഥാന വരികളുടെ ഒരു രേഖീയ സംയോജനമാണ്: . തുടങ്ങിയവ.

സിദ്ധാന്തം 3. (ഡിറ്റർമിനന്റ് പൂജ്യത്തിന് തുല്യമാകുന്നതിന് ആവശ്യമായതും മതിയായതുമായ വ്യവസ്ഥ). n-ആം ഓർഡർ ഡിറ്റർമിനന്റ് D പൂജ്യത്തിന് തുല്യമാകുന്നതിന്, അതിന്റെ വരികൾ (നിരകൾ) രേഖീയമായി ആശ്രയിക്കേണ്ടത് ആവശ്യവും മതിയായതുമാണ്.

തെളിവ് (പേജ്.40). ആവശ്യം. nth ഓർഡർ ഡിറ്റർമിനന്റ് D പൂജ്യത്തിന് തുല്യമാണെങ്കിൽ, അതിന്റെ മാട്രിക്സിന്റെ അടിസ്ഥാന മൈനർ ഓർഡർ r ആണ്

അങ്ങനെ, ഒരു വരി മറ്റുള്ളവരുടെ രേഖീയ സംയോജനമാണ്. തുടർന്ന്, സിദ്ധാന്തം 1 പ്രകാരം, ഡിറ്റർമിനന്റിന്റെ വരികൾ രേഖീയമായി ആശ്രയിച്ചിരിക്കുന്നു.

പര്യാപ്തത. D വരികൾ രേഖീയമായി ആശ്രിതമാണെങ്കിൽ, സിദ്ധാന്തം 1 പ്രകാരം A i എന്നത് ശേഷിക്കുന്ന വരികളുടെ രേഖീയ സംയോജനമാണ്. D യുടെ മൂല്യം മാറ്റാതെ A i എന്ന സ്ട്രിംഗിൽ നിന്ന് നിർദ്ദിഷ്ട ലീനിയർ കോമ്പിനേഷൻ കുറച്ചാൽ നമുക്ക് ഒരു പൂജ്യം സ്ട്രിംഗ് ലഭിക്കും. അതിനാൽ, ഡിറ്റർമിനന്റുകളുടെ ഗുണങ്ങൾ അനുസരിച്ച്, D=0. തുടങ്ങിയവ.

സിദ്ധാന്തം 4.പ്രാഥമിക പരിവർത്തന സമയത്ത്, മാട്രിക്സിന്റെ റാങ്ക് മാറില്ല.

തെളിവ്. ഡിറ്റർമിനന്റുകളുടെ ഗുണവിശേഷതകൾ പരിഗണിക്കുമ്പോൾ കാണിച്ചിരിക്കുന്നതുപോലെ, സ്ക്വയർ മെട്രിക്സുകൾ രൂപാന്തരപ്പെടുത്തുമ്പോൾ, അവയുടെ ഡിറ്റർമിനന്റുകൾ ഒന്നുകിൽ മാറില്ല, അല്ലെങ്കിൽ പൂജ്യമല്ലാത്ത സംഖ്യ കൊണ്ട് ഗുണിക്കുക, അല്ലെങ്കിൽ ചിഹ്നം മാറ്റുക. ഈ സാഹചര്യത്തിൽ, ഒറിജിനൽ മാട്രിക്സിന്റെ സീറോ അല്ലാത്ത പ്രായപൂർത്തിയാകാത്തവരുടെ ഏറ്റവും ഉയർന്ന ക്രമം സംരക്ഷിക്കപ്പെടുന്നു, അതായത്. മാട്രിക്സിന്റെ റാങ്ക് മാറില്ല. തുടങ്ങിയവ.

r(A)=r(B) ആണെങ്കിൽ A, B എന്നിവയാണ് തത്തുല്യം: A~B.

സിദ്ധാന്തം 5.പ്രാഥമിക പരിവർത്തനങ്ങൾ ഉപയോഗിച്ച്, നിങ്ങൾക്ക് മാട്രിക്സ് കുറയ്ക്കാൻ കഴിയും സ്റ്റെപ്പ് വ്യൂ.മാട്രിക്സ് എന്ന് വിളിക്കുന്നു പടിപടിയായി, അതിന് ഫോം ഉണ്ടെങ്കിൽ:

A=, ഇവിടെ a ii ≠0, i=1,2,...,r; r≤k.

r≤k എന്ന അവസ്ഥ എല്ലായ്പ്പോഴും ട്രാൻസ്പോസ് ചെയ്യുന്നതിലൂടെ നേടാനാകും.

സിദ്ധാന്തം 6.ഒരു എച്ചലോൺ മാട്രിക്സിന്റെ റാങ്ക് അതിന്റെ പൂജ്യമല്ലാത്ത വരികളുടെ എണ്ണത്തിന് തുല്യമാണ് .

ആ. സ്റ്റെപ്പ് മാട്രിക്സിന്റെ റാങ്ക് r ന് തുല്യമാണ്, കാരണം r എന്ന ക്രമത്തിൽ പൂജ്യമല്ലാത്ത ഒരു മൈനർ ഉണ്ട്:

മാട്രിക്സ് റാങ്ക് എന്ന ആശയം അതിന്റെ വരികളുടെയോ നിരകളുടെയോ രേഖീയ ആശ്രിതത്വം (സ്വാതന്ത്ര്യം) എന്ന ആശയവുമായി അടുത്ത ബന്ധപ്പെട്ടിരിക്കുന്നു. ഭാവിയിൽ ഞങ്ങൾ വരികൾക്കുള്ള മെറ്റീരിയൽ അവതരിപ്പിക്കും; നിരകൾക്കായി അവതരണം സമാനമാണ്.

മാട്രിക്സിൽ എഅതിന്റെ വരികൾ ഇങ്ങനെ സൂചിപ്പിക്കാം:

, , …. ,

ഒരു മാട്രിക്സിന്റെ രണ്ട് വരികൾ തുല്യമാണെന്ന് പറയപ്പെടുന്നു, അവയുടെ അനുബന്ധ ഘടകങ്ങൾ തുല്യമാണെങ്കിൽ: , എങ്കിൽ , .

മാട്രിക്സ് വരികളിലെ ഗണിത പ്രവർത്തനങ്ങൾ (ഒരു വരിയെ ഒരു സംഖ്യ കൊണ്ട് ഗുണിക്കുക, വരികൾ ചേർക്കുക) എലമെന്റ്-ബൈ-എലമെന്റ് നടത്തുന്ന പ്രവർത്തനങ്ങളായി അവതരിപ്പിക്കുന്നു:

ലൈൻ ഇസ്ട്രിംഗുകളുടെ ഒരു രേഖീയ സംയോജനത്തെ വിളിക്കുന്നു..., മാട്രിക്സ്, അനിയന്ത്രിതമായ യഥാർത്ഥ സംഖ്യകളാൽ ഈ വരികളുടെ ഉൽപ്പന്നങ്ങളുടെ ആകെത്തുകയ്ക്ക് തുല്യമാണെങ്കിൽ:

മാട്രിക്സിന്റെ വരികളെ വിളിക്കുന്നു രേഖീയമായി ആശ്രയിക്കുന്നത്, ഒരേസമയം പൂജ്യത്തിന് തുല്യമല്ലാത്ത സംഖ്യകൾ ഉണ്ടെങ്കിൽ, മാട്രിക്സ് വരികളുടെ ഒരു രേഖീയ സംയോജനം പൂജ്യം വരിക്ക് തുല്യമാണ്:

, =(0,0,...,0). (3.3)

സിദ്ധാന്തം 3.3മാട്രിക്സിന്റെ ഒരു വരിയെങ്കിലും മറ്റുള്ളവയുടെ രേഖീയ സംയോജനമാണെങ്കിൽ, മാട്രിക്സിന്റെ വരികൾ രേഖീയമായി ആശ്രയിച്ചിരിക്കുന്നു.

□ തീർച്ചയായും, തീർച്ചയായും, ഫോർമുലയിൽ (3.3) , പിന്നെ

അങ്ങനെ, വരി ശേഷിക്കുന്ന വരികളുടെ ഒരു രേഖീയ സംയോജനമാണ്. ■

വരികളുടെ (3.3) ഒരു രേഖീയ സംയോജനം പൂജ്യത്തിന് തുല്യമാണെങ്കിൽ, എല്ലാ ഗുണകങ്ങളും പൂജ്യത്തിന് തുല്യമാണെങ്കിൽ മാത്രം, വരികളെ രേഖീയമായി സ്വതന്ത്രമെന്ന് വിളിക്കുന്നു.

സിദ്ധാന്തം 3.4.(മാട്രിക്സിന്റെ റാങ്കിനെക്കുറിച്ച്) ഒരു മാട്രിക്സിന്റെ റാങ്ക് അതിന്റെ രേഖീയ സ്വതന്ത്ര വരികളുടെയോ നിരകളുടെയോ പരമാവധി എണ്ണത്തിന് തുല്യമാണ്, അതിലൂടെ അതിന്റെ മറ്റെല്ലാ വരികളും (നിരകൾ) രേഖീയമായി പ്രകടിപ്പിക്കുന്നു.

□ മാട്രിക്സ് അനുവദിക്കുക എ m n എന്ന വലുപ്പത്തിന് റാങ്ക് ഉണ്ട് ആർ(ആർമിനിറ്റ്). പൂജ്യമല്ലാത്ത ഒരു മൈനർ ഉണ്ടെന്നാണ് ഇതിനർത്ഥം ആർ-ആം ഓർഡർ. ഏതെങ്കിലും നോൺ-സീറോ മൈനർ ആർഈ ഉത്തരവിനെ അടിസ്ഥാന മൈനർ എന്ന് വിളിക്കും.

കൃത്യതയ്ക്കായി, അടിസ്ഥാനം മൈനർ ആയിരിക്കട്ടെ ലീഡിംഗ് അല്ലെങ്കിൽ കോർണർ മൈനർ. അപ്പോൾ മാട്രിക്സിന്റെ വരികൾ രേഖീയമായി സ്വതന്ത്രമാണ്. നമുക്ക് വിപരീതമായി അനുമാനിക്കാം, അതായത്, ഈ സ്ട്രിംഗുകളിലൊന്ന്, ഉദാഹരണത്തിന്, മറ്റുള്ളവയുടെ രേഖീയ സംയോജനമാണ്. ഘടകങ്ങളിൽ നിന്ന് കുറയ്ക്കുക ആർ- 1-ആം വരിയുടെ, 1-ആം വരിയുടെ മൂലകങ്ങൾ, ഗുണിച്ചാൽ , പിന്നെ 2-ആം വരിയിലെ ഘടകങ്ങൾ, ഗുണിച്ചാൽ , ... കൂടാതെ ഘടകങ്ങൾ ( r- 1) - വരികൾ ഗുണിച്ചാൽ . പ്രോപ്പർട്ടി 8 അടിസ്ഥാനമാക്കി, മാട്രിക്സിന്റെ അത്തരം പരിവർത്തനങ്ങൾക്കൊപ്പം, അതിന്റെ ഡിറ്റർമിനന്റ് D മാറില്ല, പക്ഷേ മുതൽ ആർ- വരിയിൽ ഇപ്പോൾ പൂജ്യങ്ങൾ മാത്രമേ ഉണ്ടാകൂ, അപ്പോൾ D = 0 ഒരു വൈരുദ്ധ്യമാണ്. അതിനാൽ, മാട്രിക്സിന്റെ വരികൾ രേഖീയമായി ആശ്രയിച്ചിരിക്കുന്നു എന്ന ഞങ്ങളുടെ അനുമാനം തെറ്റാണ്.

നമുക്ക് വരികൾ വിളിക്കാം അടിസ്ഥാന. മാട്രിക്സിന്റെ ഏതെങ്കിലും (r+1) വരികൾ രേഖീയമായി ആശ്രിതമാണെന്ന് നമുക്ക് കാണിക്കാം, അതായത്. ഏതൊരു സ്ട്രിംഗും അടിസ്ഥാനപരമായവയുടെ അടിസ്ഥാനത്തിൽ പ്രകടിപ്പിക്കുന്നു.

ആദ്യത്തെ ഓർഡറിന്റെ ഒരു മൈനർ (r +1) പരിഗണിക്കാം, ഇത് മറ്റൊരു വരിയുടെ ഘടകങ്ങളുമായി ചോദ്യം ചെയ്യപ്പെടുന്ന മൈനറിനെ സപ്ലിമെന്റ് ചെയ്യുന്നതിലൂടെ ലഭിക്കുന്നു. ഐകോളവും ജെ. മാട്രിക്സിന്റെ റാങ്ക് ആയതിനാൽ ഈ മൈനർ പൂജ്യമാണ് ആർ, അതിനാൽ ഏത് ഉയർന്ന ഓർഡർ മൈനറും പൂജ്യമാണ്.

അവസാന (ചേർത്ത) നിരയുടെ ഘടകങ്ങൾ അനുസരിച്ച് ഇത് വിപുലീകരിക്കുന്നു, നമുക്ക് ലഭിക്കും

അവസാന ബീജഗണിത പൂരകത്തിന്റെ മോഡുലസ് അടിസ്ഥാന മൈനറുമായി പൊരുത്തപ്പെടുന്നിടത്ത് ഡിഅതിനാൽ പൂജ്യത്തിൽ നിന്ന് വ്യത്യസ്തമാണ്, അതായത്. 0.

മാട്രിക്സ്- ഒരു നിശ്ചിത ക്രമത്തിൽ ക്രമീകരിച്ചിരിക്കുന്ന അനിയന്ത്രിതമായ സംഖ്യകളുടെ ഒരു ചതുരാകൃതിയിലുള്ള പട്ടിക, വലിപ്പം m*n (നിരകൾ പ്രകാരം നിരകൾ). മാട്രിക്സിന്റെ മൂലകങ്ങൾ നിയുക്തമാക്കിയിരിക്കുന്നത് ഇവിടെ i വരി സംഖ്യയും, aj എന്നത് നിര സംഖ്യയുമാണ്.

കൂട്ടിച്ചേർക്കൽ (കുറയ്ക്കൽ)മെട്രിക്സുകൾ ഏകമാനമായ മെട്രിക്സുകൾക്ക് മാത്രമേ നിർവചിച്ചിട്ടുള്ളൂ. മെട്രിക്സുകളുടെ ആകെത്തുക (വ്യത്യാസം) ഒരു മെട്രിക്സാണ്, അതിന്റെ മൂലകങ്ങൾ യഥാക്രമം, യഥാർത്ഥ മെട്രിക്സുകളുടെ മൂലകങ്ങളുടെ ആകെത്തുക (വ്യത്യാസം) ആണ്.

ഗുണനം (വിഭജനം)ഓരോ സംഖ്യയും- ഈ സംഖ്യകൊണ്ട് ഓരോ മാട്രിക്സ് മൂലകത്തിന്റെയും ഗുണനം (വിഭജനം).

മാട്രിക്സ് ഗുണനം മെട്രിക്സുകൾക്ക് മാത്രമേ നിർവചിച്ചിട്ടുള്ളൂ, ആദ്യത്തേതിന്റെ നിരകളുടെ എണ്ണം രണ്ടാമത്തേതിന്റെ വരികളുടെ എണ്ണത്തിന് തുല്യമാണ്.

മാട്രിക്സ് ഗുണനം- മാട്രിക്സ്, അതിന്റെ ഘടകങ്ങൾ ഫോർമുലകളാൽ നൽകിയിരിക്കുന്നു:

മാട്രിക്സ് ട്രാൻസ്പോസ്- അത്തരമൊരു മാട്രിക്സ് ബി, യഥാർത്ഥ മാട്രിക്സ് എയിലെ നിരകൾ (വരികൾ) ആയ വരികൾ (നിരകൾ). നിയുക്തമാക്കിയത്

വിപരീത മാട്രിക്സ്

മാട്രിക്സ് സമവാക്യങ്ങൾ– A*X=B ഫോമിന്റെ സമവാക്യങ്ങൾ മെട്രിക്സുകളുടെ ഒരു ഉൽപ്പന്നമാണ്, ഈ സമവാക്യത്തിനുള്ള ഉത്തരം മാട്രിക്സ് X ആണ്, ഇത് നിയമങ്ങൾ ഉപയോഗിച്ച് കണ്ടെത്തുന്നു:

1. ഒരു മാട്രിക്സിന്റെ നിരകളുടെ (വരികളുടെ) ലീനിയർ ആശ്രിതത്വവും സ്വാതന്ത്ര്യവും. ലീനിയർ ആശ്രിതത്വ മാനദണ്ഡം, മാട്രിക്സ് നിരകളുടെ (വരികൾ) ലീനിയർ ആശ്രിതത്വത്തിന് മതിയായ വ്യവസ്ഥകൾ.

വരികളുടെ (നിരകൾ) സിസ്റ്റത്തെ വിളിക്കുന്നു രേഖീയമായി സ്വതന്ത്രമായ, ലീനിയർ കോമ്പിനേഷൻ നിസ്സാരമാണെങ്കിൽ (സമത്വം a1...n=0 ആയിരിക്കുമ്പോൾ മാത്രമേ തൃപ്തികരമാകൂ), ഇവിടെ A1...n നിരകൾ (വരികൾ), aa1...n വിപുലീകരണ ഗുണകങ്ങളാണ്.

മാനദണ്ഡം: വെക്റ്ററുകളുടെ ഒരു സിസ്റ്റം രേഖീയമായി ആശ്രിതമാകുന്നതിന്, സിസ്റ്റത്തിന്റെ ശേഷിക്കുന്ന വെക്റ്ററുകളിലൂടെ സിസ്റ്റത്തിന്റെ ഒരു വെക്റ്ററെങ്കിലും രേഖീയമായി പ്രകടിപ്പിക്കേണ്ടത് ആവശ്യവും മതിയായതുമാണ്.

മതിയായ അവസ്ഥ:

1. മാട്രിക്സ് ഡിറ്റർമിനന്റുകളും അവയുടെ ഗുണങ്ങളും

മാട്രിക്സ് ഡിറ്റർമിനന്റ് (ഡിറ്റർമിനന്റ്)ഫോർമുല ഉപയോഗിച്ച് മാട്രിക്സിന്റെ ഘടകങ്ങളിൽ നിന്ന് ഒരു സ്ക്വയർ മാട്രിക്സ് എ കണക്കാക്കാൻ കഴിയുന്ന ഒരു സംഖ്യയാണ്:

, മൂലകത്തിന്റെ അധിക മൈനർ എവിടെയാണ്

പ്രോപ്പർട്ടികൾ:

1. വിപരീത മാട്രിക്സ്, വിപരീത മാട്രിക്സ് കണക്കാക്കുന്നതിനുള്ള അൽഗോരിതം.

വിപരീത മാട്രിക്സ്- അത്തരത്തിലുള്ള ഒരു സ്ക്വയർ മാട്രിക്സ് X, ഒരേ ഓർഡറിന്റെ ഒരു സ്ക്വയർ മാട്രിക്സ് A യുമായി ചേർന്ന്, വ്യവസ്ഥയെ തൃപ്തിപ്പെടുത്തുന്നു: ഇവിടെ E ആണ് A യുടെ അതേ ക്രമത്തിന്റെ ഐഡന്റിറ്റി മെട്രിക്സ്. പൂജ്യത്തിന് തുല്യമല്ലാത്ത ഡിറ്റർമിനന്റ് ഉള്ള ഏതൊരു ചതുര മാട്രിക്സിനും 1 വിപരീത മാട്രിക്സ് ഉണ്ട്. പ്രാഥമിക പരിവർത്തന രീതി ഉപയോഗിച്ചും ഫോർമുല ഉപയോഗിച്ചും കണ്ടെത്തി:

മാട്രിക്സ് റാങ്ക് എന്ന ആശയം. മൈനർ അടിസ്ഥാനത്തിലുള്ള സിദ്ധാന്തം. ഒരു മാട്രിക്സിന്റെ ഡിറ്റർമിനന്റ് പൂജ്യത്തിന് തുല്യമായിരിക്കുന്നതിനുള്ള മാനദണ്ഡം. മെട്രിക്സുകളുടെ പ്രാഥമിക പരിവർത്തനങ്ങൾ. പ്രാഥമിക പരിവർത്തന രീതി ഉപയോഗിച്ച് കണക്കുകൂട്ടലുകൾ റാങ്ക് ചെയ്യുക. പ്രാഥമിക പരിവർത്തന രീതി ഉപയോഗിച്ച് വിപരീത മാട്രിക്സിന്റെ കണക്കുകൂട്ടൽ.

മാട്രിക്സ് റാങ്ക് -മൈനർ അടിസ്ഥാന ക്രമം (rg A)

അടിസ്ഥാന മൈനർ -പൂജ്യത്തിന് തുല്യമല്ലാത്ത ക്രമത്തിന്റെ ഒരു മൈനർ r, അതായത്, r+1-ഉം അതിലും ഉയർന്നതുമായ എല്ലാ മൈനറുകളും പൂജ്യത്തിന് തുല്യമാണ് അല്ലെങ്കിൽ നിലവിലില്ല.

അടിസ്ഥാന മൈനർ സിദ്ധാന്തം -ഒരു അനിയന്ത്രിതമായ മാട്രിക്സ് എയിൽ, ഓരോ നിരയും (വരി) അടിസ്ഥാന മൈനർ സ്ഥിതിചെയ്യുന്ന നിരകളുടെ (വരി) രേഖീയ സംയോജനമാണ്.

തെളിവ്: m*n അളവുകളുടെ മാട്രിക്‌സ് A-യിലെ മൈനർ അടിസ്ഥാനം ആദ്യ r വരികളിലും ആദ്യത്തെ r നിരകളിലും സ്ഥിതിചെയ്യട്ടെ. മെട്രിക്സ് എയുടെ അടിസ്ഥാന മൈനറിലേക്ക് stth വരിയുടെയും kth നിരയുടെയും അനുബന്ധ ഘടകങ്ങൾ നൽകുന്നതിലൂടെ ലഭിക്കുന്ന ഡിറ്റർമിനന്റ് നമുക്ക് പരിഗണിക്കാം.

ഏതൊരു u യ്ക്കും ഈ ഡിറ്റർമിനന്റ് പൂജ്യത്തിന് തുല്യമാണെന്ന് ശ്രദ്ധിക്കുക. എങ്കിൽ അല്ലെങ്കിൽ, ഡിറ്റർമിനന്റ് ഡിയിൽ രണ്ട് സമാന വരികൾ അല്ലെങ്കിൽ രണ്ട് സമാന നിരകൾ അടങ്ങിയിരിക്കുന്നു. അവ ആണെങ്കിൽ, ഡിറ്റർമിനന്റ് ഡി പൂജ്യത്തിന് തുല്യമാണ്, കാരണം ഇത് (r+λ)-ro ക്രമത്തിന്റെ മൈനർ ആണ്. അവസാന വരിയിൽ ഡിറ്റർമിനന്റ് വികസിപ്പിക്കുമ്പോൾ, നമുക്ക് ലഭിക്കുന്നത് :, അവസാന വരിയിലെ മൂലകങ്ങളുടെ ബീജഗണിത പൂരകങ്ങൾ എവിടെയാണ്. ഇതൊരു അടിസ്ഥാന മൈനറായതിനാൽ ശ്രദ്ധിക്കുക. അതിനാൽ, എവിടെ അവസാന സമത്വം എഴുതുന്നത്, നമുക്ക് ലഭിക്കുന്നു , അതായത്. kth കോളം (ഏതായാലും) അടിസ്ഥാന മൈനറിന്റെ നിരകളുടെ രേഖീയ സംയോജനമാണ്, അതാണ് ഞങ്ങൾക്ക് തെളിയിക്കേണ്ടത്.

മാനദണ്ഡം ഡിetA=0– ഒരു ഡിറ്റർമിനന്റ് അതിന്റെ വരികൾ (നിരകൾ) രേഖീയമായി ആശ്രിതമാണെങ്കിൽ മാത്രം പൂജ്യത്തിന് തുല്യമാണ്.

പ്രാഥമിക പരിവർത്തനങ്ങൾ:

1) പൂജ്യം അല്ലാതെ മറ്റൊരു സംഖ്യ കൊണ്ട് ഒരു സ്ട്രിംഗിനെ ഗുണിക്കുക;

2) ഒരു വരിയുടെ ഘടകങ്ങളിലേക്ക് മറ്റൊരു വരിയുടെ മൂലകങ്ങൾ ചേർക്കുന്നു;

3) സ്ട്രിംഗുകളുടെ പുനഃക്രമീകരണം;

4) സമാനമായ വരികളിലൊന്ന് (നിരകൾ) മറികടക്കുന്നു;

5) ട്രാൻസ്പോസിഷൻ;

റാങ്ക് കണക്കുകൂട്ടൽ -അടിസ്ഥാന മൈനർ സിദ്ധാന്തത്തിൽ നിന്ന്, മാട്രിക്സ് എയുടെ റാങ്ക് പരമാവധി രേഖീയ സ്വതന്ത്ര വരികളുടെ (മാട്രിക്സിലെ നിരകൾ) തുല്യമാണ്, അതിനാൽ പ്രാഥമിക പരിവർത്തനങ്ങളുടെ ചുമതല എല്ലാ രേഖീയ സ്വതന്ത്ര വരികളും (നിരകൾ) കണ്ടെത്തുക എന്നതാണ്.

വിപരീത മാട്രിക്സ് കണക്കാക്കുന്നു- ഒരു നിശ്ചിത മാട്രിക്സ് ടിയെ മാട്രിക്സ് എ കൊണ്ട് ഗുണിച്ച് പരിവർത്തനങ്ങൾ നടപ്പിലാക്കാം, ഇത് അനുബന്ധ പ്രാഥമിക മെട്രിക്സുകളുടെ ഗുണനമാണ്: TA = E.

ഈ സമവാക്യം അർത്ഥമാക്കുന്നത് പരിവർത്തന മാട്രിക്സ് T എന്നത് മാട്രിക്സിന്റെ വിപരീത മാട്രിക്സ് ആണെന്നാണ്. അപ്പോൾ, അതിനാൽ,