ഇഷ്ടപ്പെട്ടോ? ബുക്ക്മാർക്കുകളിലേക്ക് ചേർക്കുക
സിംപ്ലക്സ് രീതി ഉപയോഗിച്ച് പ്രശ്നങ്ങൾ പരിഹരിക്കുന്നു: ഓൺലൈൻ ഉദാഹരണങ്ങൾ
ടാസ്ക് 1.കമ്പനി രണ്ട് വലുപ്പത്തിലുള്ള ബാത്ത്റൂം ഷെൽഫുകൾ നിർമ്മിക്കുന്നു - A, B. സെയിൽസ് ഏജന്റുമാർ കണക്കാക്കുന്നത് ആഴ്ചയിൽ 550 ഷെൽഫുകൾ വരെ വിപണിയിൽ വിൽക്കാൻ കഴിയുമെന്നാണ്. ഓരോ തരം A ഷെൽഫിനും 2 m2 മെറ്റീരിയൽ ആവശ്യമാണ്, ഓരോ തരം B ഷെൽഫിനും 3 m2 മെറ്റീരിയൽ ആവശ്യമാണ്. കമ്പനിക്ക് ആഴ്ചയിൽ 1200 m2 മെറ്റീരിയൽ വരെ ലഭിക്കും. ടൈപ്പ് എ യുടെ ഒരു ഷെൽഫ് നിർമ്മിക്കുന്നതിന്, 12 മിനിറ്റ് മെഷീൻ സമയം ആവശ്യമാണ്, കൂടാതെ തരം ബി - 30 മിനിറ്റ് നിർമ്മിക്കാൻ; ആഴ്ചയിൽ 160 മണിക്കൂറും യന്ത്രം ഉപയോഗിക്കാം. ടൈപ്പ് എ യുടെ ഷെൽഫുകളുടെ വിൽപ്പനയിൽ നിന്നുള്ള ലാഭം 3 മോണിറ്ററി യൂണിറ്റുകൾ ആണെങ്കിൽ, ടൈപ്പ് ബി - 4 മോണിറ്ററി യൂണിറ്റുകളിൽ നിന്ന്. യൂണിറ്റുകൾ, അപ്പോൾ ഓരോ തരത്തിലുമുള്ള എത്ര ഷെൽഫുകൾ ആഴ്ചയിൽ നിർമ്മിക്കണം?
ടാസ്ക് 2.ഒരു പ്രശ്നം പരിഹരിക്കൂ ലീനിയർ പ്രോഗ്രാമിംഗ്സിംപ്ലക്സ് രീതി. 
ടാസ്ക് 3.കമ്പനി 3 തരം ഉൽപ്പന്നങ്ങൾ നിർമ്മിക്കുന്നു: A1, A2, A3, രണ്ട് തരം അസംസ്കൃത വസ്തുക്കൾ ഉപയോഗിച്ച്. ഉൽപ്പാദന യൂണിറ്റിന് ഓരോ തരത്തിലുള്ള അസംസ്കൃത വസ്തുക്കളുടെയും ചെലവ്, ആസൂത്രണ കാലയളവിലെ അസംസ്കൃത വസ്തുക്കളുടെ കരുതൽ, അതുപോലെ ഓരോ തരത്തിലുമുള്ള ഉൽപാദന യൂണിറ്റിൽ നിന്നുള്ള ലാഭം എന്നിവ അറിയപ്പെടുന്നു.
- ലാഭം വർദ്ധിപ്പിക്കുന്നതിന് ഓരോ തരത്തിലുമുള്ള എത്ര ഇനങ്ങൾ നിർമ്മിക്കണം?
- ഓരോ തരത്തിലുള്ള അസംസ്കൃത വസ്തുക്കളുടെയും അതിന്റെ പ്രത്യേക മൂല്യത്തിന്റെയും നില നിർണ്ണയിക്കുക.
- ഓരോ തരം അസംസ്കൃത വസ്തുക്കളുടെയും ഇൻവെന്ററികളിലെ മാറ്റങ്ങൾക്ക് പരമാവധി ഇടവേള നിശ്ചയിക്കുക, അതിനുള്ളിൽ ഒപ്റ്റിമൽ പ്ലാനിന്റെ ഘടന, അതായത്. ഉൽപ്പാദന നാമകരണം മാറില്ല.
- അസംസ്കൃത വസ്തുക്കളുടെ വിരളമായ ഒന്നിന്റെ സ്റ്റോക്ക് സാധ്യമായ പരമാവധി (നിർദിഷ്ട ഔട്ട്പുട്ട് പരിധിക്കുള്ളിൽ) മൂല്യത്തിലേക്ക് വർദ്ധിപ്പിക്കുമ്പോൾ ഉൽപ്പാദിപ്പിക്കുന്ന ഉൽപ്പന്നങ്ങളുടെ അളവും ഉൽപാദനത്തിൽ നിന്നുള്ള ലാഭവും നിർണ്ണയിക്കുക.
- ഓരോ തരത്തിലുമുള്ള ഉൽപാദന യൂണിറ്റിൽ നിന്നുള്ള ലാഭത്തിലെ മാറ്റത്തിന്റെ ഇടവേളകൾ നിർണ്ണയിക്കുക ഒപ്റ്റിമൽ പ്ലാൻമാറില്ല.
ടാസ്ക് 4.ഒരു ലീനിയർ പ്രോഗ്രാമിംഗ് പ്രശ്നം പരിഹരിക്കുക സിംപ്ലക്സ് രീതി:

ടാസ്ക് 5.സിംപ്ലക്സ് രീതി ഉപയോഗിച്ച് ഒരു ലീനിയർ പ്രോഗ്രാമിംഗ് പ്രശ്നം പരിഹരിക്കുക: 
ടാസ്ക് 6.പ്രാരംഭമായി പരിഗണിച്ച്, സിംപ്ലക്സ് രീതി ഉപയോഗിച്ച് പ്രശ്നം പരിഹരിക്കുക റഫറൻസ് പ്ലാൻ, വ്യവസ്ഥയിൽ നൽകിയിരിക്കുന്ന പ്ലാൻ: 
ടാസ്ക് 7.പരിഷ്കരിച്ച സിംപ്ലക്സ് രീതി ഉപയോഗിച്ച് പ്രശ്നം പരിഹരിക്കുക.
എ, ബി എന്നീ രണ്ട് തരം ഉൽപ്പന്നങ്ങൾ നിർമ്മിക്കുന്നതിന്, മൂന്ന് തരം സാങ്കേതിക ഉപകരണങ്ങൾ ഉപയോഗിക്കുന്നു. ഉൽപ്പന്നം A യുടെ ഒരു യൂണിറ്റ് നിർമ്മിക്കുന്നതിന്, ആദ്യ തരത്തിലുള്ള ഉപകരണങ്ങൾ a1=4 മണിക്കൂർ, രണ്ടാമത്തെ തരം a2=8 മണിക്കൂർ, മൂന്നാം തരം a3=9 മണിക്കൂർ ഉപകരണങ്ങൾ എന്നിവ ഉപയോഗിക്കുന്നു. ഉൽപ്പന്നം B യുടെ ഒരു യൂണിറ്റ് നിർമ്മിക്കുന്നതിന്, ആദ്യ തരത്തിലുള്ള ഉപകരണങ്ങൾ b1=7 മണിക്കൂർ, രണ്ടാമത്തെ തരം b2=3 മണിക്കൂർ ഉപകരണങ്ങൾ, മൂന്നാം തരം b3=5 മണിക്കൂർ എന്നിവ ഉപയോഗിക്കുന്നു.
ഈ ഉൽപ്പന്നങ്ങളുടെ ഉത്പാദനത്തിനായി ആദ്യ തരത്തിലുള്ള ഉപകരണങ്ങൾക്ക് t1=49 മണിക്കൂറിൽ കൂടുതൽ പ്രവർത്തിക്കാൻ കഴിയും, രണ്ടാമത്തെ തരത്തിലുള്ള ഉപകരണങ്ങൾ t2=51 മണിക്കൂറിൽ കൂടരുത്, മൂന്നാമത്തെ തരത്തിലുള്ള ഉപകരണങ്ങൾ t3=45 മണിക്കൂറിൽ കൂടരുത്.
പൂർത്തിയായ ഉൽപ്പന്നം A യുടെ ഒരു യൂണിറ്റ് വിൽപ്പനയിൽ നിന്നുള്ള ലാഭം ALPHA = 6 റൂബിൾ ആണ്, ഉൽപ്പന്നം B BETTA = 5 റൂബിൾ ആണ്.
എ, ബി ഉൽപ്പന്നങ്ങൾക്കായി ഒരു പ്രൊഡക്ഷൻ പ്ലാൻ തയ്യാറാക്കുക, ഉറപ്പാക്കുക പരമാവധി ലാഭംഅവ നടപ്പിലാക്കുന്നതിൽ നിന്ന്.
ടാസ്ക് 8.കണ്ടെത്തുക ഒപ്റ്റിമൽ പരിഹാരംഡ്യുവൽ സിംപ്ലക്സ് രീതി 
പ്രശ്ന പ്രസ്താവനയിൽ ≥ ചിഹ്നമുള്ള നിയന്ത്രണങ്ങൾ അടങ്ങിയിട്ടുണ്ടെങ്കിൽ, അസമത്വത്തിന്റെ ഇരുവശങ്ങളെയും -1 കൊണ്ട് ഗുണിച്ച് അവയെ ∑a ji b j എന്ന രൂപത്തിലേക്ക് ചുരുക്കാം. നമുക്ക് m അധിക വേരിയബിളുകൾ x n+j ≥0(j =1,m) അവതരിപ്പിക്കുകയും നിയന്ത്രണങ്ങളെ തുല്യതയുടെ രൂപത്തിലേക്ക് മാറ്റുകയും ചെയ്യാം.
![]() (2)
(2)
എല്ലാം പ്രാരംഭമായി എന്ന് നമുക്ക് അനുമാനിക്കാം ടാസ്ക് വേരിയബിളുകൾ x 1 , x 2 ,..., x n - അടിസ്ഥാനപരമല്ലാത്തത്. അപ്പോൾ അധിക വേരിയബിളുകൾ അടിസ്ഥാനമായിരിക്കും, കൂടാതെ നിയന്ത്രണങ്ങളുടെ സിസ്റ്റത്തിന് ഒരു പ്രത്യേക പരിഹാരത്തിന് രൂപം ഉണ്ട്
x 1 = x 2 = ... = x n = 0, x n+ j = b j, j =1,m. (3)
ഈ സാഹചര്യത്തിൽ F 0 = 0 എന്ന ഗോൾ ഫംഗ്ഷന്റെ മൂല്യം, നമുക്ക് F(x) യെ ഇനിപ്പറയുന്ന രീതിയിൽ പ്രതിനിധീകരിക്കാം:
F(x)=∑c i x i +F 0 =0 (4)
പ്രാരംഭ സിംപ്ലക്സ് പട്ടിക (സിംപ്ലക്സ് പട്ടിക 1) സമവാക്യങ്ങൾ (2), (4) എന്നിവയെ അടിസ്ഥാനമാക്കിയാണ് സമാഹരിച്ചിരിക്കുന്നത്. അധിക വേരിയബിളുകൾ x n+j ന് മുമ്പായി ഒരു “+” ചിഹ്നം ഉണ്ടെങ്കിൽ, (2) പോലെ, വേരിയബിളുകൾക്ക് മുന്നിലുള്ള എല്ലാ ഗുണകങ്ങളും x i, സ്വതന്ത്ര പദമായ b j എന്നിവ മാറ്റങ്ങളില്ലാതെ സിംപ്ലക്സ് പട്ടികയിൽ നൽകപ്പെടും. ലക്ഷ്യം ഫംഗ്ഷൻ പരമാവധിയാക്കുമ്പോൾ, സിംപ്ലക്സ് പട്ടികയുടെ താഴത്തെ വരിയിൽ വിപരീത ചിഹ്നങ്ങളോടെ ഗുണകങ്ങൾ നൽകപ്പെടുന്നു. സിംപ്ലക്സ് പട്ടികയിലെ സ്വതന്ത്ര നിബന്ധനകൾ പ്രശ്നത്തിനുള്ള പരിഹാരം നിർണ്ണയിക്കുന്നു.
പ്രശ്നം പരിഹരിക്കുന്നതിനുള്ള അൽഗോരിതം ഇപ്രകാരമാണ്:
1st ഘട്ടം. സ്വതന്ത്ര അംഗങ്ങളുടെ കോളത്തിലെ അംഗങ്ങളെ കാണുന്നു. അവയെല്ലാം പോസിറ്റീവ് ആണെങ്കിൽ, അനുവദനീയമായ ഒരു അടിസ്ഥാന പരിഹാരം കണ്ടെത്തി, അൽഗോരിതത്തിന്റെ 5-ാം ഘട്ടത്തിലേക്ക് പോകണം, ഇത് ഒപ്റ്റിമൽ പരിഹാരം കണ്ടെത്തുന്നതിന് അനുയോജ്യമാണ്. പ്രാരംഭ സിംപ്ലക്സ് പട്ടികയിൽ നെഗറ്റീവ് ഫ്രീ നിബന്ധനകളുണ്ടെങ്കിൽ, പരിഹാരം സാധുതയുള്ളതല്ല, നിങ്ങൾ ഘട്ടം 2-ലേക്ക് പോകണം.
രണ്ടാം ഘട്ടം. അനുവദനീയമായ ഒരു പരിഹാരം കണ്ടെത്തുന്നതിന്, അത് നടപ്പിലാക്കുന്നു, അടിസ്ഥാനപരമല്ലാത്ത വേരിയബിളുകളിൽ ഏതാണ് അടിസ്ഥാനത്തിൽ ഉൾപ്പെടുത്തേണ്ടതെന്നും ഏത് വേരിയബിളാണ് അടിസ്ഥാനത്തിൽ നിന്ന് നീക്കം ചെയ്യേണ്ടതെന്നും തീരുമാനിക്കേണ്ടത് ആവശ്യമാണ്.
പട്ടിക 1.
| അടിസ്ഥാന വേരിയബിളുകൾ | നിയന്ത്രണങ്ങൾക്ക് കീഴിൽ സ്വതന്ത്ര അംഗങ്ങൾ | അടിസ്ഥാനമല്ലാത്ത വേരിയബിളുകൾ | |||||
| x 1 | x 2 | ... | x l | ... | x n|||
| x n+1 | ബി 1 | ഒരു 11 | ഒരു 12 | ... | ഒരു 1ലി | ... | ഒരു 1n |
| x n+2 | ബി 2 | ഒരു 21 | ഒരു 22 | ... | ഒരു 2l | ... | ഒരു 2n |
| . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . |
| x n+r | b2 | ഒരു r1 | ഒരു r2 | ... | ഒരു ആർഎൽ | ... | arn |
| . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . |
| x n+m | ബി എം | ഒരു m1 | ഒരു m2 | ... | ഒരു മില്ലി | ... | ഒരു മി |
| F(x)പരമാവധി | എഫ് 0 | -സി 1 | -സി 2 | ... | -സി 1 | ... | -സി എൻ |
ഇത് ചെയ്യുന്നതിന്, സ്വതന്ത്ര പദങ്ങളുടെ നിരയിലെ ഏതെങ്കിലും നെഗറ്റീവ് ഘടകങ്ങളെ തിരഞ്ഞെടുക്കുക (അത് b 2 ലീഡിംഗ് ആയിരിക്കട്ടെ, അല്ലെങ്കിൽ പരിഹരിക്കുന്നു. ഒരു നെഗറ്റീവ് ഫ്രീ ടേം ഉള്ള നിരയിൽ നെഗറ്റീവ് ഘടകങ്ങളൊന്നും ഇല്ലെങ്കിൽ, നിയന്ത്രണങ്ങളുടെ സിസ്റ്റം സ്ഥിരതയില്ലാത്തതും പ്രശ്നത്തിന് പരിഹാരമില്ല.
അതേ സമയം, തിരഞ്ഞെടുത്ത NP x l വർദ്ധിക്കുമ്പോൾ ആദ്യം അടയാളം മാറ്റുന്ന വേരിയബിൾ ബിപിയിൽ നിന്ന് ഒഴിവാക്കിയിരിക്കുന്നു. ഇത് x n+r ആയിരിക്കും, ഇതിന്റെ സൂചിക r വ്യവസ്ഥയിൽ നിന്ന് നിർണ്ണയിക്കപ്പെടുന്നു

ആ. തിരഞ്ഞെടുത്ത മുൻനിര നിരയുടെ മൂലകവുമായി സ്വതന്ത്ര പദത്തിന്റെ ഏറ്റവും ചെറിയ അനുപാതമുള്ള വേരിയബിൾ. ഈ ബന്ധത്തെ വിളിക്കുന്നു ലളിതമായ ബന്ധം. പോസിറ്റീവ് സിംപ്ലക്സ് ബന്ധങ്ങൾ മാത്രമേ പരിഗണിക്കാവൂ.
x n+r എന്ന വേരിയബിളുമായി ബന്ധപ്പെട്ട വരിയെ വിളിക്കുന്നു നയിക്കുന്നത്, അല്ലെങ്കിൽ അനുവദിക്കുന്നത്. സിംപ്ലെക്സ് പട്ടിക a rl ന്റെ മൂലകത്തെ, ലീഡിംഗ് വരിയുടെയും ലീഡിംഗ് കോളത്തിന്റെയും കവലയിൽ സ്ഥിതി ചെയ്യുന്നതിനെ ലീഡിംഗ് അല്ലെങ്കിൽ പരിഹരിക്കുന്ന ഘടകം എന്ന് വിളിക്കുന്നു.മുൻനിര ഘടകം കണ്ടെത്തുന്നത് ഓരോ സാധാരണ സിംപ്ലക്സ് ടേബിളിലും ജോലി അവസാനിപ്പിക്കുന്നു.
3-ആം ഘട്ടം. ഒരു പുതിയ സിംപ്ലക്സ് ടേബിൾ കണക്കാക്കുന്നു, മുൻ ഘട്ടത്തിലെ സിംപ്ലെക്സ് ടേബിളിന്റെ ഘടകങ്ങളിൽ നിന്ന് അതിന്റെ ഘടകങ്ങൾ വീണ്ടും കണക്കാക്കുകയും ഒരു പ്രൈം ഉപയോഗിച്ച് അടയാളപ്പെടുത്തുകയും ചെയ്യുന്നു, അതായത്. b" j , a" ji , c" i , F" 0 . ഇനിപ്പറയുന്ന സൂത്രവാക്യങ്ങൾ ഉപയോഗിച്ച് ഘടകങ്ങൾ വീണ്ടും കണക്കാക്കുന്നു:

ആദ്യം, പുതിയ സിംപ്ലക്സ് ടേബിൾ മുമ്പത്തെ സിംപ്ലെക്സ് ടേബിളിൽ മുന്നിലുണ്ടായിരുന്ന വരിയും നിരയും പൂരിപ്പിക്കും. എക്സ്പ്രഷൻ (5) അർത്ഥമാക്കുന്നത് മുൻനിര മൂലകത്തിന്റെ സ്ഥാനത്തുള്ള a" rl എന്ന മൂലകം മുമ്പത്തെ സിംപ്ലെക്സ് പട്ടികയിലെ മൂലകത്തിന്റെ പരസ്പര ബന്ധത്തിന് തുല്യമാണ് എന്നാണ്. a ri എന്ന വരിയിലെ മൂലകങ്ങളെ മുൻനിര മൂലകവും മൂലകങ്ങളുടെ ഘടകങ്ങളും കൊണ്ട് ഹരിക്കുന്നു. കോളം a jl എന്നിവയും മുൻനിര ഘടകത്താൽ വിഭജിക്കപ്പെടുന്നു, പക്ഷേ വിപരീത ചിഹ്നം ഉപയോഗിച്ചാണ് എടുക്കുന്നത്. b" r, c" l എന്നീ മൂലകങ്ങൾ ഒരേ തത്വമനുസരിച്ച് കണക്കാക്കുന്നു.
ബാക്കിയുള്ള സൂത്രവാക്യങ്ങൾ ഉപയോഗിച്ച് എളുപ്പത്തിൽ എഴുതാം.
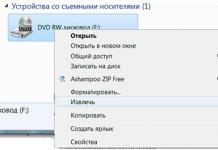
പഴയ സിംപ്ലക്സ് ടേബിളിന് അനുസൃതമായി ദീർഘചതുരം നിർമ്മിച്ചിരിക്കുന്നത്, അതിന്റെ ഡയഗണലുകളിൽ ഒന്ന് വീണ്ടും കണക്കാക്കിയ (a ji), ലീഡിംഗ് (a rl) ഘടകങ്ങൾ (ചിത്രം 1) എന്നിവയാൽ രൂപം കൊള്ളുന്ന വിധത്തിലാണ്. രണ്ടാമത്തെ ഡയഗണൽ അദ്വിതീയമായി നിർണ്ണയിക്കപ്പെടുന്നു. ഒരു പുതിയ മൂലകം a" ji കണ്ടെത്തുന്നതിന്, മുൻ മൂലകത്താൽ ഹരിച്ച വിപരീത ഡയഗണലിന്റെ മൂലകങ്ങളുടെ ഗുണനം a ji എന്ന മൂലകത്തിൽ നിന്ന് കുറയ്ക്കുന്നു (ഇത് സെല്ലിന് അടുത്തുള്ള "-" ചിഹ്നത്താൽ സൂചിപ്പിക്കുന്നു). ഘടകങ്ങൾ b" j, (j≠r), c" i എന്നിവ അതേ രീതിയിൽ വീണ്ടും കണക്കാക്കുന്നു. (i≠l).
4-ആം ഘട്ടം. പുതിയ സിംപ്ലക്സ് പട്ടികയുടെ വിശകലനം ആരംഭിക്കുന്നത് അൽഗോരിതത്തിന്റെ ആദ്യ ഘട്ടത്തിലാണ്. പ്രായോഗികമായ ഒരു അടിസ്ഥാന പരിഹാരം കണ്ടെത്തുന്നതുവരെ പ്രവർത്തനം തുടരും, അതായത്. ഫ്ലോട്ട് കോളത്തിന്റെ എല്ലാ ഘടകങ്ങളും പോസിറ്റീവ് ആയിരിക്കണം.
അഞ്ചാം ഘട്ടം. സ്വീകാര്യമായ ഒരു അടിസ്ഥാന പരിഹാരം കണ്ടെത്തിയെന്ന് ഞങ്ങൾ വിശ്വസിക്കുന്നു. ഗോൾ ഫംഗ്ഷന്റെ വരിയുടെ ഗുണകങ്ങൾ ഞങ്ങൾ നോക്കുന്നു F(x) . ഒരു സിംപ്ലെക്സ് ടേബിളിന്റെ ഒപ്റ്റിമലിറ്റിയുടെ ഒരു അടയാളം എഫ്-വരിയിലെ നോൺ-ബേസിക് വേരിയബിളുകൾക്കുള്ള ഗുണകങ്ങളുടെ നോൺ-നെഗറ്റിവിറ്റിയാണ്.

അരി. 1. ദീർഘചതുരം നിയമം
എഫ്-വരിയിലെ ഗുണകങ്ങളിൽ നെഗറ്റീവ് ആയവ (സൌജന്യ പദം ഒഴികെ) ഉണ്ടെങ്കിൽ, നിങ്ങൾ മറ്റൊരു അടിസ്ഥാന പരിഹാരത്തിലേക്ക് പോകേണ്ടതുണ്ട്. ഒബ്ജക്റ്റീവ് ഫംഗ്ഷൻ പരമാവധിയാക്കുമ്പോൾ, അടിസ്ഥാനത്തിൽ അടിസ്ഥാനമല്ലാത്ത വേരിയബിളുകളിലൊന്ന് ഉൾപ്പെടുന്നു (ഉദാഹരണത്തിന് x l), അതിന്റെ കോളം പരമാവധി തുല്യമാണ് യഥാർത്ഥ മൂല്യംനെഗറ്റീവ് കോഫിഫിഷ്യന്റ് സി എൽ ഇൻ താഴെ വരിസിംപ്ലക്സ് പട്ടികകൾ. ലക്ഷ്യം ഫംഗ്ഷന്റെ പുരോഗതിയിലേക്ക് നയിക്കുന്ന വേരിയബിൾ തിരഞ്ഞെടുക്കാൻ ഇത് നിങ്ങളെ അനുവദിക്കുന്നു. x l എന്ന വേരിയബിളുമായി ബന്ധപ്പെട്ട നിരയെ ലീഡിംഗ് കോളം എന്ന് വിളിക്കുന്നു. അതേ സമയം, ആ വേരിയബിൾ x n+r അടിസ്ഥാനത്തിൽ നിന്ന് ഒഴിവാക്കിയിരിക്കുന്നു, ഇതിന്റെ സൂചിക r നിർണ്ണയിക്കുന്നത് ഏറ്റവും കുറഞ്ഞ സിംപ്ലക്സ് ബന്ധമാണ്:
x n+r എന്നതുമായി ബന്ധപ്പെട്ട വരിയെ ലീഡിംഗ് എന്ന് വിളിക്കുന്നു, കൂടാതെ സിംപ്ലെക്സ് ടേബിളിന്റെ മൂലകത്തെ a rl, ലീഡിംഗ് വരിയുടെയും ലീഡിംഗ് കോളത്തിന്റെയും കവലയിൽ നിൽക്കുന്നതിനെ വിളിക്കുന്നു. പ്രമുഖ ഘടകം.
ആറാം ഘട്ടം. ഘട്ടം 3 ൽ പറഞ്ഞിരിക്കുന്ന നിയമങ്ങൾ അനുസരിച്ച്. ഒപ്റ്റിമൽ പരിഹാരം കണ്ടെത്തുന്നതുവരെ അല്ലെങ്കിൽ അത് നിലവിലില്ലെന്ന് നിഗമനം ചെയ്യുന്നതുവരെ നടപടിക്രമം തുടരുന്നു.
സൊല്യൂഷൻ ഒപ്റ്റിമൈസേഷൻ സമയത്ത്, ലീഡിംഗ് കോളത്തിലെ എല്ലാ ഘടകങ്ങളും പോസിറ്റീവ് അല്ലെങ്കിൽ, ലീഡിംഗ് വരി തിരഞ്ഞെടുക്കാൻ കഴിയില്ല. ഈ സാഹചര്യത്തിൽ, പ്രശ്നത്തിനുള്ള സാദ്ധ്യമായ പരിഹാരങ്ങളുടെ മേഖലയിലെ പ്രവർത്തനം F max ->&∞ മുകളിൽ പരിമിതപ്പെടുത്തിയിട്ടില്ല.
ഒരു എക്സ്ട്രീം തിരയുന്നതിന്റെ അടുത്ത ഘട്ടത്തിൽ, അടിസ്ഥാന വേരിയബിളുകളിലൊന്ന് മാറുകയാണെങ്കിൽ പൂജ്യത്തിന് തുല്യം, അപ്പോൾ അനുബന്ധ അടിസ്ഥാന പരിഹാരത്തെ ഡീജനറേറ്റ് എന്ന് വിളിക്കുന്നു. ഈ സാഹചര്യത്തിൽ, സൈക്ലിംഗ് എന്ന് വിളിക്കപ്പെടുന്നവ സംഭവിക്കുന്നു, ബിപികളുടെ അതേ സംയോജനം ഒരു നിശ്ചിത ആവൃത്തിയിൽ ആവർത്തിക്കാൻ തുടങ്ങുന്നു (ഫംഗ്ഷൻ എഫ് മൂല്യം സംരക്ഷിക്കപ്പെടുന്നു) കൂടാതെ പുതിയ പ്രായോഗിക അടിസ്ഥാന പരിഹാരത്തിലേക്ക് നീങ്ങുന്നത് അസാധ്യമാണ്. . സിംപ്ലക്സ് രീതിയുടെ പ്രധാന പോരായ്മകളിലൊന്നാണ് ലൂപ്പിംഗ്, പക്ഷേ ഇത് താരതമ്യേന അപൂർവമാണ്. പ്രായോഗികമായി, അത്തരം സന്ദർഭങ്ങളിൽ, ഗോൾ ഫംഗ്ഷനിലെ നെഗറ്റീവ് ഗുണകത്തിന്റെ പരമാവധി കേവല മൂല്യവുമായി പൊരുത്തപ്പെടുന്ന നിരയുടെ അടിസ്ഥാനത്തിലേക്ക് പ്രവേശിക്കാൻ അവർ സാധാരണയായി വിസമ്മതിക്കുകയും നിർമ്മിക്കുകയും ചെയ്യുന്നു. ക്രമരഹിതമായ തിരഞ്ഞെടുപ്പ്പുതിയ അടിസ്ഥാന പരിഹാരം.
ഉദാഹരണം 1. പ്രശ്നം പരിഹരിക്കുക
പരമാവധി(F(x) = -2x 1 + 5x 2 | 2x 1 + x 2 ≤7; x 1 + 4x 2 ≥8; x 2 ≤4; x 1.2 ≥0)
സിംപ്ലക്സ് രീതി ഉപയോഗിച്ച് പരിഹാര പ്രക്രിയയുടെ ജ്യാമിതീയ വ്യാഖ്യാനം നൽകുക.
പ്രശ്നത്തിനുള്ള പരിഹാരത്തിന്റെ ഗ്രാഫിക്കൽ വ്യാഖ്യാനം ചിത്രത്തിൽ അവതരിപ്പിച്ചിരിക്കുന്നു. 2. കോർഡിനേറ്റുകളുള്ള ODZP യുടെ ശീർഷകത്തിൽ ലക്ഷ്യം പ്രവർത്തനത്തിന്റെ പരമാവധി മൂല്യം കൈവരിക്കുന്നു. സിംപ്ലക്സ് ടേബിളുകൾ ഉപയോഗിച്ച് നമുക്ക് പ്രശ്നം പരിഹരിക്കാം. നമുക്ക് രണ്ടാമത്തെ പരിമിതിയെ (-1) കൊണ്ട് ഗുണിച്ച് അസമത്വങ്ങളെ തുല്യതയുടെ രൂപത്തിലേക്ക് കൊണ്ടുവരാൻ അധിക വേരിയബിളുകൾ അവതരിപ്പിക്കാം.

ഞങ്ങൾ പ്രാരംഭ വേരിയബിളുകൾ x 1, x 2 എന്നിവ അടിസ്ഥാനപരമല്ലാത്തതായി എടുക്കുന്നു, കൂടാതെ അധിക x 3, x 4, x 5 എന്നിവ അടിസ്ഥാനമായി കണക്കാക്കുകയും ഒരു സിംപ്ലക്സ് പട്ടിക (സിംപ്ലക്സ് പട്ടിക 2) രചിക്കുകയും ചെയ്യുന്നു. സിംപ്ലക്സ് പട്ടികയുമായി ബന്ധപ്പെട്ട പരിഹാരം. 2, സാധുതയില്ല; മുൻകാല അൽഗോരിതം ഘട്ടം 2 അനുസരിച്ച് മുൻനിര ഘടകം രൂപരേഖ തയ്യാറാക്കുകയും തിരഞ്ഞെടുക്കുകയും ചെയ്യുന്നു. ഇനിപ്പറയുന്ന സിംപ്ലക്സ് പട്ടിക. 3 അനുവദനീയമായ ഒരു അടിസ്ഥാന പരിഹാരം നിർവചിക്കുന്നു; ചിത്രം 1 ലെ ODZP യുടെ ശീർഷകം അതിനോട് യോജിക്കുന്നു. 2 പ്രശ്നപരിഹാര അൽഗോരിതത്തിന്റെ അഞ്ചാം ഘട്ടത്തിന് അനുസൃതമായി മുൻനിര ഘടകം രൂപരേഖ തയ്യാറാക്കുകയും തിരഞ്ഞെടുക്കുകയും ചെയ്യുന്നു. മേശ 4 പ്രശ്നത്തിനുള്ള ഒപ്റ്റിമൽ പരിഹാരവുമായി യോജിക്കുന്നു, അതിനാൽ: x 1 = x 5 = 0; x 2 = 4; x 3 = 3; x 4 = 8; എഫ് പരമാവധി = 20.


അരി. 2. ഗ്രാഫിക് പരിഹാരംചുമതലകൾ
ഈ രീതി ഒരു ലീനിയർ പ്രോഗ്രാമിംഗ് പ്രശ്നത്തിനുള്ള റഫറൻസ് സൊല്യൂഷനുകളുടെ ഉദ്ദേശ്യത്തോടെയുള്ള എണ്ണൽ രീതിയാണ്. ഒപ്റ്റിമൽ സൊല്യൂഷൻ കണ്ടെത്തുന്നതിനോ ഒപ്റ്റിമൽ സൊല്യൂഷൻ ഇല്ലെന്ന് സ്ഥാപിക്കുന്നതിനോ പരിമിതമായ ഘട്ടങ്ങളിൽ ഇത് അനുവദിക്കുന്നു.
സിംപ്ലക്സ് രീതിയുടെ പ്രധാന ഉള്ളടക്കം ഇപ്രകാരമാണ്:- ഒപ്റ്റിമൽ റഫറൻസ് പരിഹാരം കണ്ടെത്തുന്നതിനുള്ള ഒരു രീതി സൂചിപ്പിക്കുക
- ഒരു റഫറൻസ് സൊല്യൂഷനിൽ നിന്ന് മറ്റൊന്നിലേക്ക് മാറുന്ന രീതി സൂചിപ്പിക്കുക, അതിൽ ഒബ്ജക്റ്റീവ് ഫംഗ്ഷന്റെ മൂല്യം ഒപ്റ്റിമൽ ഒന്നിനോട് അടുക്കും, അതായത്. റഫറൻസ് സൊല്യൂഷൻ മെച്ചപ്പെടുത്തുന്നതിനുള്ള ഒരു മാർഗം സൂചിപ്പിക്കുക
- ഒപ്റ്റിമൽ സൊല്യൂഷനിൽ സപ്പോർട്ട് സൊല്യൂഷനുകൾക്കായി തിരയുന്നത് പെട്ടെന്ന് നിർത്താൻ നിങ്ങളെ അനുവദിക്കുന്ന മാനദണ്ഡങ്ങൾ സജ്ജമാക്കുക അല്ലെങ്കിൽ ഒപ്റ്റിമൽ സൊല്യൂഷന്റെ അഭാവത്തെക്കുറിച്ച് ഒരു നിഗമനത്തിലെത്തുക.
ലീനിയർ പ്രോഗ്രാമിംഗ് പ്രശ്നങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള സിംപ്ലക്സ് രീതിയുടെ അൽഗോരിതം
സിംപ്ലക്സ് രീതി ഉപയോഗിച്ച് ഒരു പ്രശ്നം പരിഹരിക്കുന്നതിന്, നിങ്ങൾ ഇനിപ്പറയുന്നവ ചെയ്യണം:- പ്രശ്നം കാനോനിക്കൽ രൂപത്തിലേക്ക് കൊണ്ടുവരിക
- “യൂണിറ്റ് അടിസ്ഥാനം” ഉപയോഗിച്ച് പ്രാരംഭ പിന്തുണാ പരിഹാരം കണ്ടെത്തുക (പിന്തുണ പരിഹാരമില്ലെങ്കിൽ, നിയന്ത്രണ സംവിധാനത്തിന്റെ പൊരുത്തക്കേട് കാരണം പ്രശ്നത്തിന് പരിഹാരമില്ല)
- റഫറൻസ് സൊല്യൂഷനെ അടിസ്ഥാനമാക്കി വെക്റ്റർ വിഘടനത്തിന്റെ എസ്റ്റിമേറ്റ് കണക്കാക്കി സിംപ്ലക്സ് രീതിയുടെ പട്ടിക പൂരിപ്പിക്കുക
- ഒപ്റ്റിമൽ പരിഹാരത്തിന്റെ അദ്വിതീയതയുടെ മാനദണ്ഡം തൃപ്തികരമാണെങ്കിൽ, പ്രശ്നത്തിന്റെ പരിഹാരം അവസാനിക്കുന്നു
- ഒരു കൂട്ടം ഒപ്റ്റിമൽ സൊല്യൂഷനുകളുടെ നിലനിൽപ്പിനുള്ള വ്യവസ്ഥ പാലിക്കുകയാണെങ്കിൽ, എല്ലാ ഒപ്റ്റിമൽ സൊല്യൂഷനുകളും ലളിതമായ കണക്കെടുപ്പിലൂടെ കണ്ടെത്തും.
സിംപ്ലക്സ് രീതി ഉപയോഗിച്ച് ഒരു പ്രശ്നം പരിഹരിക്കുന്നതിനുള്ള ഒരു ഉദാഹരണം
ഉദാഹരണം 26.1സിംപ്ലക്സ് രീതി ഉപയോഗിച്ച് പ്രശ്നം പരിഹരിക്കുക:
പരിഹാരം:
ഞങ്ങൾ പ്രശ്നം കാനോനിക്കൽ രൂപത്തിലേക്ക് കൊണ്ടുവരുന്നു.
ഈ ആവശ്യത്തിനായി ഇൻ ഇടത് വശംആദ്യത്തെ അസമത്വ പരിമിതിക്ക്, ഞങ്ങൾ +1 ന്റെ കോഫിഫിഷ്യന്റ് ഉള്ള ഒരു അധിക വേരിയബിൾ x 6 അവതരിപ്പിക്കുന്നു. x 6 എന്ന വേരിയബിൾ ഒബ്ജക്റ്റീവ് ഫംഗ്ഷനിൽ പൂജ്യത്തിന്റെ ഒരു കോഫിഫിഷ്യന്റ് ഉള്ളതാണ് (അതായത്, ഇത് ഉൾപ്പെടുത്തിയിട്ടില്ല).
നമുക്ക് ലഭിക്കുന്നത്:

ഞങ്ങൾ പ്രാഥമിക പിന്തുണ പരിഹാരം കണ്ടെത്തുന്നു. ഇത് ചെയ്യുന്നതിന്, ഞങ്ങൾ സ്വതന്ത്ര (പരിഹരിക്കപ്പെടാത്ത) വേരിയബിളുകളെ പൂജ്യം x1 = x2 = x3 = 0 ലേക്ക് തുല്യമാക്കുന്നു.
നമുക്ക് ലഭിക്കുന്നു റഫറൻസ് പരിഹാരം X1 = (0,0,0,24,30,6) യൂണിറ്റ് അടിസ്ഥാനത്തിൽ B1 = (A4, A5, A6).
ഞങ്ങൾ കണക്കാക്കുന്നു വെക്റ്റർ വിഘടനത്തിന്റെ ഏകദേശ കണക്കുകൾഫോർമുല അനുസരിച്ച് റഫറൻസ് പരിഹാരത്തിന്റെ അടിസ്ഥാനത്തിൽ വ്യവസ്ഥകൾ:
Δ k = C b X k - c k
- C b = (c 1, c 2, ..., c m) - അടിസ്ഥാന വേരിയബിളുകൾക്കുള്ള ഒബ്ജക്റ്റീവ് ഫംഗ്ഷന്റെ ഗുണകങ്ങളുടെ വെക്റ്റർ
- X k = (x 1k, x 2k, ..., x mk) - റഫറൻസ് സൊല്യൂഷന്റെ അടിസ്ഥാനം അനുസരിച്ച് അനുബന്ധ വെക്റ്റർ A k യുടെ വികാസത്തിന്റെ വെക്റ്റർ
- x k എന്ന വേരിയബിളിന്റെ ഒബ്ജക്റ്റീവ് ഫംഗ്ഷന്റെ ഗുണകമാണ് C k.

അടിസ്ഥാനത്തിൽ ഉൾപ്പെടുത്തിയിരിക്കുന്ന വെക്റ്ററുകളുടെ കണക്കുകൾ എല്ലായ്പ്പോഴും പൂജ്യത്തിന് തുല്യമാണ്. റഫറൻസ് സൊല്യൂഷൻ, വിപുലീകരണ ഗുണകങ്ങൾ, റഫറൻസ് സൊല്യൂഷൻ അടിസ്ഥാനമാക്കിയുള്ള അവസ്ഥ വെക്റ്ററുകളുടെ വികാസത്തിന്റെ എസ്റ്റിമേറ്റ് എന്നിവ എഴുതിയിരിക്കുന്നു സിംപ്ലക്സ് ടേബിൾ:

പട്ടികയുടെ മുകളിൽ, എസ്റ്റിമേറ്റുകളുടെ കണക്കുകൂട്ടൽ എളുപ്പത്തിനായി, വസ്തുനിഷ്ഠമായ പ്രവർത്തനത്തിന്റെ ഗുണകങ്ങൾ എഴുതിയിരിക്കുന്നു. "ബി" എന്ന ആദ്യ നിരയിൽ റഫറൻസ് സൊല്യൂഷന്റെ അടിസ്ഥാനത്തിൽ ഉൾപ്പെടുത്തിയിരിക്കുന്ന വെക്റ്ററുകൾ എഴുതിയിരിക്കുന്നു. ഈ വെക്ടറുകൾ എഴുതിയിരിക്കുന്ന ക്രമം കൺസ്ട്രൈന്റ് ഇക്വേഷനുകളിലെ അനുവദനീയമായ അജ്ഞാതരുടെ എണ്ണവുമായി പൊരുത്തപ്പെടുന്നു. "സി ബി" പട്ടികയുടെ രണ്ടാമത്തെ നിരയിൽ അടിസ്ഥാന വേരിയബിളുകൾക്കുള്ള ഒബ്ജക്റ്റീവ് ഫംഗ്ഷന്റെ ഗുണകങ്ങൾ അതേ ക്രമത്തിൽ എഴുതിയിരിക്കുന്നു. ചെയ്തത് ശരിയായ സ്ഥാനംഅടിസ്ഥാനത്തിൽ ഉൾപ്പെടുത്തിയിരിക്കുന്ന യൂണിറ്റ് വെക്റ്ററുകളുടെ എസ്റ്റിമേറ്റിന്റെ "C b" നിരയിലെ ഒബ്ജക്റ്റീവ് ഫംഗ്ഷന്റെ ഗുണകങ്ങൾ എല്ലായ്പ്പോഴും പൂജ്യത്തിന് തുല്യമാണ്.
"A 0" നിരയിലെ Δ k യുടെ എസ്റ്റിമേറ്റുകളുള്ള പട്ടികയുടെ അവസാന വരിയിൽ, Z (X 1) എന്ന റഫറൻസ് സൊല്യൂഷനിലെ ഒബ്ജക്റ്റീവ് ഫംഗ്ഷന്റെ മൂല്യങ്ങൾ എഴുതിയിരിക്കുന്നു.
പ്രാരംഭ പിന്തുണ സൊല്യൂഷൻ ഒപ്റ്റിമൽ അല്ല, കാരണം പരമാവധി പ്രശ്നത്തിൽ വെക്ടറുകൾ A 1, A 3 എന്നിവയ്ക്ക് Δ 1 = -2, Δ 3 = -9 എന്നിവ നെഗറ്റീവ് ആണ്.
പിന്തുണാ പരിഹാരം മെച്ചപ്പെടുത്തുന്നതിനുള്ള സിദ്ധാന്തം അനുസരിച്ച്, പരമാവധി പ്രശ്നത്തിൽ കുറഞ്ഞത് ഒരു വെക്റ്ററിനെങ്കിലും നെഗറ്റീവ് എസ്റ്റിമേറ്റ് ഉണ്ടെങ്കിൽ, ഒബ്ജക്റ്റീവ് ഫംഗ്ഷന്റെ മൂല്യം കൂടുതലുള്ള ഒരു പുതിയ പിന്തുണാ പരിഹാരം നിങ്ങൾക്ക് കണ്ടെത്താനാകും.
രണ്ട് വെക്റ്ററുകളിൽ ഏതാണ് ഒബ്ജക്റ്റീവ് ഫംഗ്ഷനിൽ വലിയ വർദ്ധനവിന് കാരണമാകുന്നതെന്ന് നമുക്ക് നിർണ്ണയിക്കാം.
ഒബ്ജക്റ്റീവ് ഫംഗ്ഷന്റെ വർദ്ധനവ് ഫോർമുല ഉപയോഗിച്ച് കണ്ടെത്തുന്നു: .
ഫോർമുല ഉപയോഗിച്ച് ആദ്യത്തെയും മൂന്നാമത്തെയും നിരകൾക്കായി θ 01 പാരാമീറ്ററിന്റെ മൂല്യങ്ങൾ ഞങ്ങൾ കണക്കാക്കുന്നു:
l = 1-ന് θ 01 = 6, l = 1-ന് θ 03 = 3 (പട്ടിക 26.1).
ആദ്യ വെക്റ്റർ ΔZ 1 = - 6*(- 2) = 12, മൂന്നാമത്തെ വെക്റ്റർ ΔZ 3 = - 3*(- 9) = 27 എന്നിവയെ അടിസ്ഥാനമാക്കി അവതരിപ്പിക്കുമ്പോൾ ഒബ്ജക്റ്റീവ് ഫംഗ്ഷന്റെ വർദ്ധനവ് ഞങ്ങൾ കണ്ടെത്തുന്നു.
തൽഫലമായി, ഒപ്റ്റിമൽ സൊല്യൂഷനിലേക്കുള്ള വേഗത്തിലുള്ള സമീപനത്തിന്, അടിസ്ഥാന A6 ന്റെ ആദ്യ വെക്റ്ററിന് പകരം റഫറൻസ് സൊല്യൂഷന്റെ അടിസ്ഥാനത്തിൽ വെക്റ്റർ A3 അവതരിപ്പിക്കേണ്ടത് ആവശ്യമാണ്, കാരണം θ 03 എന്ന പാരാമീറ്ററിന്റെ ഏറ്റവും കുറഞ്ഞ ഭാഗം ആദ്യ വരിയിൽ കൈവരിക്കുന്നു ( l = 1).
X13 = 2 എന്ന ഘടകം ഉപയോഗിച്ച് ഞങ്ങൾ ജോർദാൻ പരിവർത്തനം നടത്തുന്നു, B2 = (A3, A4, A5) അടിസ്ഥാനത്തിലുള്ള രണ്ടാമത്തെ റഫറൻസ് സൊല്യൂഷൻ X2 = (0,0,3,21,42,0) നമുക്ക് ലഭിക്കും. (പട്ടിക 26.2)

ഈ പരിഹാരം ഒപ്റ്റിമൽ അല്ല, കാരണം വെക്റ്റർ A2 ന് നെഗറ്റീവ് എസ്റ്റിമേറ്റ് Δ2 = - 6. പരിഹാരം മെച്ചപ്പെടുത്തുന്നതിന്, റഫറൻസ് സൊല്യൂഷന്റെ അടിസ്ഥാനത്തിൽ വെക്റ്റർ A2 അവതരിപ്പിക്കേണ്ടത് ആവശ്യമാണ്.
അടിസ്ഥാനത്തിൽ നിന്ന് ഉരുത്തിരിഞ്ഞ വെക്റ്ററിന്റെ എണ്ണം ഞങ്ങൾ നിർണ്ണയിക്കുന്നു. ഇത് ചെയ്യുന്നതിന്, ഞങ്ങൾ രണ്ടാമത്തെ നിരയ്ക്ക് θ 02 എന്ന പരാമീറ്റർ കണക്കാക്കുന്നു, അത് l = 2 ന് 7 ന് തുല്യമാണ്. തൽഫലമായി, ഞങ്ങൾ അടിസ്ഥാനത്തിൽ നിന്ന് രണ്ടാമത്തെ അടിസ്ഥാന വെക്റ്റർ A4 നേടുന്നു. x 22 = 3 എന്ന മൂലകം ഉപയോഗിച്ച് ഞങ്ങൾ ജോർദാൻ പരിവർത്തനം നടത്തുന്നു, ഞങ്ങൾക്ക് മൂന്നാമത്തെ റഫറൻസ് പരിഹാരം X3 = (0,7,10,0,63,0) B2 = (A3, A2, A5) (പട്ടിക 26.3) ലഭിക്കും.

ഈ പരിഹാരം മാത്രമാണ് ഏറ്റവും ഒപ്റ്റിമൽ, കാരണം അടിസ്ഥാനത്തിൽ ഉൾപ്പെടുത്തിയിട്ടില്ലാത്ത എല്ലാ വെക്റ്ററുകൾക്കും എസ്റ്റിമേറ്റുകൾ പോസിറ്റീവ് ആണ്
Δ 1 = 7/2, Δ 4 = 2, Δ 6 = 7/2.
ഉത്തരം: max Z(X) = 201 at X = (0.7,10,0.63).
സാമ്പത്തിക വിശകലനത്തിൽ ലീനിയർ പ്രോഗ്രാമിംഗ് രീതി
ലീനിയർ പ്രോഗ്രാമിംഗ് രീതിഏറ്റവും ഒപ്റ്റിമൽ ന്യായീകരിക്കുന്നത് സാധ്യമാക്കുന്നു സാമ്പത്തിക തീരുമാനംഉൽപാദനത്തിൽ ഉപയോഗിക്കുന്ന വിഭവങ്ങളുമായി (സ്ഥിര ആസ്തികൾ, മെറ്റീരിയലുകൾ, തൊഴിൽ വിഭവങ്ങൾ) സംബന്ധിച്ച കടുത്ത നിയന്ത്രണങ്ങളുടെ സാഹചര്യങ്ങളിൽ. സാമ്പത്തിക വിശകലനത്തിൽ ഈ രീതി ഉപയോഗിക്കുന്നത് പ്രധാനമായും ഒരു ഓർഗനൈസേഷന്റെ പ്രവർത്തനങ്ങൾ ആസൂത്രണം ചെയ്യുന്നതുമായി ബന്ധപ്പെട്ട പ്രശ്നങ്ങൾ പരിഹരിക്കുന്നത് സാധ്യമാക്കുന്നു. ഈ രീതി ഒപ്റ്റിമൽ ഔട്ട്പുട്ട് ലെവലുകൾ നിർണ്ണയിക്കാൻ സഹായിക്കുന്നു, അതുപോലെ തന്നെ ഏറ്റവും കൂടുതൽ കാര്യങ്ങൾക്കുള്ള ദിശകളും ഫലപ്രദമായ ഉപയോഗംസ്ഥാപനത്തിന് ലഭ്യമായ ഉൽപ്പാദന വിഭവങ്ങൾ.
ഈ രീതി ഉപയോഗിച്ച്, അങ്ങേയറ്റത്തെ പ്രശ്നങ്ങൾ എന്ന് വിളിക്കപ്പെടുന്നവ പരിഹരിക്കപ്പെടുന്നു, അതിൽ അങ്ങേയറ്റത്തെ മൂല്യങ്ങൾ കണ്ടെത്തുന്നതിൽ ഉൾപ്പെടുന്നു, അതായത്, പരമാവധി, കുറഞ്ഞ പ്രവർത്തനങ്ങൾ വേരിയബിളുകൾ.
ഈ കാലയളവ് സിസ്റ്റത്തിന്റെ പരിഹാരത്തെ അടിസ്ഥാനമാക്കിയുള്ളതാണ് രേഖീയ സമവാക്യങ്ങൾവിശകലനം ചെയ്ത സാമ്പത്തിക പ്രതിഭാസങ്ങൾ രേഖീയമായി, കർശനമായി ബന്ധിപ്പിച്ചിരിക്കുന്ന സന്ദർഭങ്ങളിൽ പ്രവർത്തനപരമായ ആശ്രിതത്വം. ചില പരിമിത ഘടകങ്ങളുടെ സാന്നിധ്യത്തിൽ വേരിയബിളുകൾ വിശകലനം ചെയ്യാൻ ലീനിയർ പ്രോഗ്രാമിംഗ് രീതി ഉപയോഗിക്കുന്നു.
ലീനിയർ പ്രോഗ്രാമിംഗ് രീതി ഉപയോഗിച്ച് ഗതാഗത പ്രശ്നം എന്ന് വിളിക്കപ്പെടുന്ന പ്രശ്നം പരിഹരിക്കുന്നത് വളരെ സാധാരണമാണ്. ഈ ടാസ്ക്കിന്റെ ഉള്ളടക്കം പ്രവർത്തനവുമായി ബന്ധപ്പെട്ട് ഉണ്ടാകുന്ന ചിലവ് കുറയ്ക്കുക എന്നതാണ് വാഹനംവാഹനങ്ങളുടെ എണ്ണം, അവയുടെ വാഹകശേഷി, അവയുടെ പ്രവർത്തന കാലയളവ്, അറ്റകുറ്റപ്പണികൾ ആവശ്യമാണെങ്കിൽ എന്നിവ സംബന്ധിച്ച നിലവിലുള്ള നിയന്ത്രണങ്ങൾക്ക് കീഴിൽ പരമാവധി അളവ്ഉപഭോക്താക്കൾ.
കൂടാതെ, ഈ രീതിഷെഡ്യൂളിംഗ് പ്രശ്നങ്ങൾ പരിഹരിക്കുന്നതിന് വ്യാപകമായി ഉപയോഗിക്കുന്നു. തന്നിരിക്കുന്ന ഓർഗനൈസേഷന്റെ ഉദ്യോഗസ്ഥർക്കുള്ള പ്രവർത്തന സമയത്തിന്റെ വിതരണം ഈ ടാസ്ക്കിൽ അടങ്ങിയിരിക്കുന്നു, അത് ഈ ഉദ്യോഗസ്ഥരിലെ അംഗങ്ങൾക്കും ഓർഗനൈസേഷന്റെ ക്ലയന്റുകൾക്കും ഏറ്റവും സ്വീകാര്യമായിരിക്കും.
ലഭ്യമായ സ്റ്റാഫ് അംഗങ്ങളുടെ എണ്ണത്തിലും പ്രവർത്തന സമയ ഫണ്ടിലും ഉള്ള പരിമിതികളുടെ വ്യവസ്ഥകളിൽ സേവനമനുഷ്ഠിക്കുന്ന ക്ലയന്റുകളുടെ എണ്ണം പരമാവധി വർദ്ധിപ്പിക്കുക എന്നതാണ് ഈ ചുമതല.
അതിനാൽ, പ്ലേസ്മെന്റിലും ഉപയോഗ വിശകലനത്തിലും ലീനിയർ പ്രോഗ്രാമിംഗ് രീതി വളരെ സാധാരണമാണ്. വിവിധ തരംവിഭവങ്ങൾ, അതുപോലെ തന്നെ ഓർഗനൈസേഷനുകളുടെ പ്രവർത്തനങ്ങൾ ആസൂത്രണം ചെയ്യുന്നതിനും പ്രവചിക്കുന്നതിനുമുള്ള പ്രക്രിയയിൽ.
എന്നിരുന്നാലും, ആ സാമ്പത്തിക പ്രതിഭാസങ്ങൾക്ക് ഗണിതശാസ്ത്ര പ്രോഗ്രാമിംഗ് പ്രയോഗിക്കാവുന്നതാണ്, അവ തമ്മിലുള്ള ബന്ധം രേഖീയമല്ല. ഈ ആവശ്യത്തിനായി, നോൺ-ലീനിയർ, ഡൈനാമിക്, കോൺവെക്സ് പ്രോഗ്രാമിംഗ് രീതികൾ ഉപയോഗിക്കാം.
നോൺ-ലീനിയർ പ്രോഗ്രാമിംഗ് ഒബ്ജക്റ്റീവ് ഫംഗ്ഷന്റെ അല്ലെങ്കിൽ പരിമിതികളുടെ നോൺ-ലീനിയർ സ്വഭാവത്തെ ആശ്രയിച്ചിരിക്കുന്നു, അല്ലെങ്കിൽ രണ്ടും. ഈ അവസ്ഥകളിലെ വസ്തുനിഷ്ഠമായ പ്രവർത്തനത്തിന്റെ രൂപങ്ങളും അസമത്വ നിയന്ത്രണങ്ങളും വ്യത്യസ്തമായിരിക്കും.
സാമ്പത്തിക വിശകലനത്തിൽ നോൺ-ലീനിയർ പ്രോഗ്രാമിംഗ് ഉപയോഗിക്കുന്നു, പ്രത്യേകിച്ചും, ഒരു ഓർഗനൈസേഷന്റെ പ്രവർത്തനങ്ങളുടെ കാര്യക്ഷമതയും ഈ പ്രവർത്തനത്തിന്റെ അളവും, ഉൽപാദനച്ചെലവിന്റെ ഘടന, വിപണി സാഹചര്യങ്ങൾ മുതലായവ പ്രകടിപ്പിക്കുന്ന സൂചകങ്ങൾ തമ്മിലുള്ള ബന്ധം സ്ഥാപിക്കുമ്പോൾ.
ഡൈനാമിക് പ്രോഗ്രാമിംഗ് ഒരു ഡിസിഷൻ ട്രീ നിർമ്മിക്കുന്നതിനെ അടിസ്ഥാനമാക്കിയുള്ളതാണ്. ഈ വൃക്ഷത്തിന്റെ ഓരോ നിരയും അനന്തരഫലങ്ങൾ നിർണ്ണയിക്കുന്നതിനുള്ള ഒരു ഘട്ടമായി വർത്തിക്കുന്നു മുൻ തീരുമാനംഈ പരിഹാരത്തിനുള്ള ഫലപ്രദമല്ലാത്ത ഓപ്ഷനുകൾ ഇല്ലാതാക്കാനും. അങ്ങനെ, ഡൈനാമിക് പ്രോഗ്രാമിംഗ്ഒരു മൾട്ടി-സ്റ്റെപ്പ്, മൾട്ടി-സ്റ്റേജ് സ്വഭാവമുണ്ട്. കണ്ടെത്തുന്നതിന് സാമ്പത്തിക വിശകലനത്തിൽ ഇത്തരത്തിലുള്ള പ്രോഗ്രാമിംഗ് ഉപയോഗിക്കുന്നു ഒപ്റ്റിമൽ ഓപ്ഷനുകൾഇന്നും ഭാവിയിലും സംഘടനയുടെ വികസനം.
കോൺവെക്സ് പ്രോഗ്രാമിംഗ് ഒരു തരം നോൺ ലീനിയർ പ്രോഗ്രാമിംഗ് ആണ്. ഈ തരത്തിലുള്ള പ്രോഗ്രാമിംഗ് ഒരു ഓർഗനൈസേഷന്റെ പ്രവർത്തനങ്ങളുടെ ഫലങ്ങളും അതിന്റെ ചെലവുകളും തമ്മിലുള്ള ബന്ധത്തിന്റെ രേഖീയമല്ലാത്ത സ്വഭാവം പ്രകടിപ്പിക്കുന്നു. കോൺവെക്സ് (അതായത് കോൺകേവ്) പ്രോഗ്രാമിംഗ് കോൺവെക്സ് വിശകലനം ചെയ്യുന്നു വസ്തുനിഷ്ഠമായ പ്രവർത്തനങ്ങൾകുത്തനെയുള്ള നിയന്ത്രണ സംവിധാനങ്ങളും (പോയിന്റുകൾ സ്വീകാര്യമായ മൂല്യങ്ങൾ). ചെലവ് കുറയ്ക്കുക എന്ന ലക്ഷ്യത്തോടെ സാമ്പത്തിക പ്രവർത്തനങ്ങളുടെ വിശകലനത്തിൽ കോൺവെക്സ് പ്രോഗ്രാമിംഗ് ഉപയോഗിക്കുന്നു, കൂടാതെ വിശകലനം ചെയ്ത സൂചകങ്ങളെ വിപരീതമായി സ്വാധീനിക്കുന്ന ഘടകങ്ങളുടെ പ്രവർത്തനത്തിൽ നിലവിലുള്ള നിയന്ത്രണങ്ങൾക്ക് കീഴിൽ വരുമാനം വർദ്ധിപ്പിക്കുക എന്ന ലക്ഷ്യത്തോടെ കോൺകേവ് പ്രോഗ്രാമിംഗ് ഉപയോഗിക്കുന്നു. തൽഫലമായി, പരിഗണനയിലിരിക്കുന്ന പ്രോഗ്രാമിംഗ് തരങ്ങൾക്കൊപ്പം, കോൺവെക്സ് ഒബ്ജക്റ്റീവ് ഫംഗ്ഷനുകൾ ചെറുതാക്കുകയും കോൺകേവ് ഒബ്ജക്റ്റീവ് ഫംഗ്ഷനുകൾ പരമാവധിയാക്കുകയും ചെയ്യുന്നു.
സിംപ്ലക്സ് ടേബിളുകൾ ഉപയോഗിച്ച് നിങ്ങൾക്ക് ഒരു ലീനിയർ പ്രോഗ്രാമിംഗ് പ്രശ്നം പരിഹരിക്കണമെങ്കിൽ, ഞങ്ങളുടെ ഓൺലൈൻ സേവനംനിങ്ങൾക്ക് വലിയ സഹായമായിരിക്കും. ഫംഗ്ഷൻ തീവ്രമായ മൂല്യം എടുക്കുന്ന ശീർഷകം കണ്ടെത്തുന്നതിന് സ്വീകാര്യമായ മൂല്യങ്ങളുടെ ശ്രേണിയുടെ എല്ലാ ശീർഷകങ്ങളിലൂടെയും തുടർച്ചയായി തിരയുന്നത് സിംപ്ലക്സ് രീതിയിൽ ഉൾപ്പെടുന്നു. ആദ്യ ഘട്ടത്തിൽ, ചില പരിഹാരം കണ്ടെത്തി, അത് ഓരോ തുടർന്നുള്ള ഘട്ടത്തിലും മെച്ചപ്പെടുത്തുന്നു. ഈ പരിഹാരത്തെ അടിസ്ഥാനം എന്ന് വിളിക്കുന്നു. സിംപ്ലക്സ് രീതി ഉപയോഗിച്ച് ഒരു ലീനിയർ പ്രോഗ്രാമിംഗ് പ്രശ്നം പരിഹരിക്കുമ്പോൾ പ്രവർത്തനങ്ങളുടെ ക്രമം ഇതാ:
ആദ്യത്തെ പടി. സമാഹരിച്ച പട്ടികയിൽ, ഒന്നാമതായി, നിങ്ങൾ സ്വതന്ത്ര അംഗങ്ങളുള്ള കോളം നോക്കേണ്ടതുണ്ട്. അതിൽ നെഗറ്റീവ് ഘടകങ്ങൾ ഉണ്ടെങ്കിൽ, രണ്ടാമത്തെ ഘട്ടത്തിലേക്ക് പോകേണ്ടത് ആവശ്യമാണ്, ഇല്ലെങ്കിൽ, അഞ്ചാം ഘട്ടത്തിലേക്ക്.
രണ്ടാം ഘട്ടം. രണ്ടാം ഘട്ടത്തിൽ, സിംപ്ലക്സ് ടേബിൾ വീണ്ടും കണക്കാക്കുന്നതിന് ഏത് വേരിയബിളിനെ അടിസ്ഥാനത്തിൽ നിന്ന് ഒഴിവാക്കണമെന്നും ഏതൊക്കെ ഉൾപ്പെടുത്തണമെന്നും തീരുമാനിക്കേണ്ടത് ആവശ്യമാണ്. ഇത് ചെയ്യുന്നതിന്, സ്വതന്ത്ര നിബന്ധനകളുള്ള കോളത്തിലൂടെ നോക്കുക, അതിൽ ഒരു നെഗറ്റീവ് ഘടകം കണ്ടെത്തുക. നെഗറ്റീവ് ഘടകമുള്ള വരിയെ ലീഡിംഗ് എന്ന് വിളിക്കും. അതിൽ ഞങ്ങൾ മൊഡ്യൂലസിൽ പരമാവധി നെഗറ്റീവ് ഘടകം കണ്ടെത്തുന്നു, അനുബന്ധ കോളം സ്ലേവ് ആണ്. സ്വതന്ത്ര പദങ്ങൾക്കിടയിൽ നെഗറ്റീവ് മൂല്യങ്ങൾ ഉണ്ടെങ്കിലും അനുബന്ധ വരിയിൽ ഒന്നുമില്ലെങ്കിൽ, അത്തരമൊരു പട്ടികയ്ക്ക് പരിഹാരങ്ങൾ ഉണ്ടാകില്ല. സ്വതന്ത്ര പദങ്ങളുടെ നിരയിൽ സ്ഥിതിചെയ്യുന്ന മുൻനിര വരിയിലെ വേരിയബിൾ അടിസ്ഥാനത്തിൽ നിന്ന് ഒഴിവാക്കിയിരിക്കുന്നു, കൂടാതെ മുൻനിര നിരയുമായി ബന്ധപ്പെട്ട വേരിയബിൾ അടിസ്ഥാനത്തിൽ ഉൾപ്പെടുത്തിയിട്ടുണ്ട്.
പട്ടിക 1.
| അടിസ്ഥാന വേരിയബിളുകൾ | നിയന്ത്രണങ്ങൾക്ക് കീഴിൽ സ്വതന്ത്ര അംഗങ്ങൾ | അടിസ്ഥാനമല്ലാത്ത വേരിയബിളുകൾ | |||||
| x 1 | x 2 | ... | x l | ... | x n | ||
| x n+1 | ബി 1 | ഒരു 11 | ഒരു 12 | ... | ഒരു 1ലി | ... | ഒരു 1n |
| x n+2 | ബി 2 | ഒരു 21 | ഒരു 22 | ... | ഒരു 2l | ... | ഒരു 2n |
| . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . |
| x n+r | b2 | ഒരു r1 | ഒരു r2 | ... | ഒരു ആർഎൽ | ... | arn |
| . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . |
| x n+m | ബി എം | ഒരു m1 | ഒരു m2 | ... | ഒരു മില്ലി | ... | ഒരു മി |
| F(x)പരമാവധി | എഫ് 0 | -സി 1 | -സി 2 | ... | -സി 1 | ... | -സി എൻ |
മൂന്നാം ഘട്ടം. മൂന്നാം ഘട്ടത്തിൽ, പ്രത്യേക സൂത്രവാക്യങ്ങൾ ഉപയോഗിച്ച് ഞങ്ങൾ മുഴുവൻ സിംപ്ലക്സ് പട്ടികയും വീണ്ടും കണക്കാക്കുന്നു; ഈ സൂത്രവാക്യങ്ങൾ ഉപയോഗിച്ച് കാണാൻ കഴിയും.
നാലാം ഘട്ടം. വീണ്ടും കണക്കാക്കിയ ശേഷം, സ്വതന്ത്ര പദങ്ങളുടെ നിരയിൽ നെഗറ്റീവ് ഘടകങ്ങൾ അവശേഷിക്കുന്നുണ്ടെങ്കിൽ, ആദ്യ ഘട്ടത്തിലേക്ക് പോകുക; ഒന്നുമില്ലെങ്കിൽ, അഞ്ചാമത്തേതിലേക്ക്.
അഞ്ചാം പടി. നിങ്ങൾ അഞ്ചാം ഘട്ടത്തിൽ എത്തിയിട്ടുണ്ടെങ്കിൽ, സ്വീകാര്യമായ ഒരു പരിഹാരം നിങ്ങൾ കണ്ടെത്തി. എന്നിരുന്നാലും, ഇത് ഒപ്റ്റിമൽ ആണെന്ന് ഇതിനർത്ഥമില്ല. F-string-ലെ എല്ലാ ഘടകങ്ങളും പോസിറ്റീവ് ആണെങ്കിൽ മാത്രമേ അത് ഒപ്റ്റിമൽ ആകുകയുള്ളൂ. ഇത് അങ്ങനെയല്ലെങ്കിൽ, പരിഹാരം മെച്ചപ്പെടുത്തേണ്ടത് ആവശ്യമാണ്, അതിനായി അടുത്ത വീണ്ടും കണക്കുകൂട്ടലിനായി മുൻനിര വരിയും നിരയും ഞങ്ങൾ കണ്ടെത്തുന്നു ഇനിപ്പറയുന്ന അൽഗോരിതത്തിലേക്ക്. തുടക്കത്തിൽ, ഫംഗ്ഷൻ മൂല്യം ഒഴികെയുള്ള ഏറ്റവും കുറഞ്ഞ നെഗറ്റീവ് നമ്പർ സ്ട്രിംഗ് എഫ് ൽ ഞങ്ങൾ കണ്ടെത്തുന്നു. ഈ നമ്പറുള്ള കോളം മുൻനിരയിലായിരിക്കും. മുൻനിര വരി കണ്ടെത്തുന്നതിന്, അനുബന്ധ സൗജന്യ പദത്തിന്റെയും മുൻ നിരയിൽ നിന്നുള്ള ഘടകത്തിന്റെയും അനുപാതം ഞങ്ങൾ കണ്ടെത്തുന്നു, അവ പോസിറ്റീവ് ആണെങ്കിൽ. ഏറ്റവും കുറഞ്ഞ അനുപാതം നിങ്ങളെ മുൻനിര ലൈൻ നിർണ്ണയിക്കാൻ അനുവദിക്കും. ഫോർമുലകൾ ഉപയോഗിച്ച് ഞങ്ങൾ വീണ്ടും പട്ടിക വീണ്ടും കണക്കാക്കുന്നു, അതായത്. ഘട്ടം 3-ലേക്ക് പോകുക.
| - | x 1 | + | x 2 | - | എസ് 1 | = | 1 | ||||||||||
| x 1 | +3 | x 2 | + | എസ് 2 | = | 15 | |||||||||||
| - | 2 | x 1 | + | x 2 | + | എസ് 3 | = | 4 |
| - | x 1 | + | x 2 | - | എസ് 1 | + | R 1 | = | 1 | |||||||||||
| x 1 | +3 | x 2 | + | എസ് 2 | = | 15 | ||||||||||||||
| - | 2 | x 1 | + | x 2 | + | എസ് 3 | = | 4 |
| x 1 = 0 x 2 = 0 S 1 = 0 S 2 = 15 S 3 = 4 R 1 = 1 |
=> W = 1 |
| x 1 | x 2 | എസ് 1 | എസ് 2 | എസ് 3 | R 1 | സെന്റ്. അംഗം | Θ |
| -1 | 1 | -1 | 0 | 0 | 1 | 1 | 1: 1 = 1 |
| 1 | 3 | 0 | 1 | 0 | 0 | 15 | 15: 3 = 5 |
| -2 | 1 | 0 | 0 | 1 | 0 | 4 | 4: 1 = 4 |
| 1 | -1 | 1 | 0 | 0 | 0 | W - 1 | |
| -1 | 1 | -1 | 0 | 0 | 1 | 1 | |
| 4 | 0 | 3 | 1 | 0 | -3 | 12 | |
| -1 | 0 | 1 | 0 | 1 | -1 | 3 | |
| 0 | 0 | 0 | 0 | 0 | 1 | W - 0 |
| - | x 1 | + | x 2 | - | എസ് 1 | = | 1 | ||||||||||
| 4 | x 1 | + | 3 | എസ് 1 | + | എസ് 2 | = | 12 | |||||||||
| - | x 1 | + | എസ് 1 | + | എസ് 3 | = | 3 |
| x 1 | x 2 | എസ് 1 | എസ് 2 | എസ് 3 | സെന്റ്. അംഗം | Θ |
| -1 | 1 | -1 | 0 | 0 | 1 | |
| 4 | 0 | 3 | 1 | 0 | 12 | 12: 4 = 3 |
| -1 | 0 | 1 | 0 | 1 | 3 | |
| 4 | 0 | 1 | 0 | 0 | എഫ് - 1 | |
| -1 | 1 | -1 | 0 | 0 | 1 | |
| 1 | 0 | 3/4 | 1/4 | 0 | 3 | |
| -1 | 0 | 1 | 0 | 1 | 3 | |
| 4 | 0 | 1 | 0 | 0 | എഫ് - 1 | |
| 0 | 1 | -1/4 | 1/4 | 0 | 4 | |
| 1 | 0 | 3/4 | 1/4 | 0 | 3 | |
| 0 | 0 | 7/4 | 1/4 | 1 | 6 | |
| 0 | 0 | -2 | -1 | 0 | എഫ് - 13 |
| എസ് 1 = 0 എസ് 2 = 0 x 1 = 3 x 2 = 4 S 3 = 6 |
=> F - 13 = 0 => F = 13 |