ഓൺലൈൻ ഇന്റർപോളേഷൻ പ്രോഗ്രാം. ലീനിയർ ഇന്റർപോളേഷൻ

ലോക്കൽ ഇന്റർപോളേഷന്റെ ഏറ്റവും ലളിതവും ഏറ്റവും സാധാരണയായി ഉപയോഗിക്കുന്നതുമായ തരം ലീനിയർ ഇന്റർപോളേഷൻ. നൽകിയിരിക്കുന്ന പോയിന്റുകൾ ഇതിൽ അടങ്ങിയിരിക്കുന്നു ( x ഐ , വൈ ഐ) at ( i = 0. 1, ..., n) നേരായ സെഗ്‌മെന്റുകളും ഫംഗ്‌ഷനും ഉപയോഗിച്ച് ബന്ധിപ്പിച്ചിരിക്കുന്നു എഫ്(x) ഈ പോയിന്റുകളിൽ ലംബങ്ങളുള്ള ഒരു പോളിലൈൻ അടുക്കുന്നു.

തകർന്ന വരയുടെ ഓരോ സെഗ്മെന്റിന്റെയും സമവാക്യങ്ങൾ പൊതുവെ വ്യത്യസ്തമാണ്. n ഇടവേളകൾ ഉള്ളതിനാൽ ( x ഐ - 1, x ഐ), തുടർന്ന് അവയിൽ ഓരോന്നിനും രണ്ട് പോയിന്റുകളിലൂടെ കടന്നുപോകുന്ന ഒരു നേർരേഖയുടെ സമവാക്യം ഇന്റർപോളേഷൻ പോളിനോമിയലിന്റെ സമവാക്യമായി ഉപയോഗിക്കുന്നു. പ്രത്യേകിച്ചും, i-th ഇടവേളയ്ക്ക് നമുക്ക് പോയിന്റുകളിലൂടെ കടന്നുപോകുന്ന ഒരു നേർരേഖയുടെ സമവാക്യം എഴുതാം ( x ഐ -1, വൈ ഐ -1 ) ഒപ്പം ( x ഐ , വൈ ഐ), പോലെ

y=a i x+b i, x i-1 xx i

a i =

അതിനാൽ, ലീനിയർ ഇന്റർപോളേഷൻ ഉപയോഗിക്കുമ്പോൾ, നിങ്ങൾ ആദ്യം ആർഗ്യുമെന്റ് x ന്റെ മൂല്യം വീഴുന്ന ഇടവേള നിർണ്ണയിക്കേണ്ടതുണ്ട്, തുടർന്ന് അത് ഫോർമുലയിലേക്ക് (*) മാറ്റി ഈ ഘട്ടത്തിൽ ഫംഗ്ഷന്റെ ഏകദേശ മൂല്യം കണ്ടെത്തുക.

ചിത്രം 3-3-ലീനിയർ ഇന്റർപോളേഷൻ ഗ്രാഫ്.

ഒരു പ്രൊഫഷണൽ പ്രശ്നം പരിഹരിക്കുന്നു

ഞങ്ങൾ പരീക്ഷണാത്മക ഡാറ്റ പരിപാലിക്കുന്നു

ഉത്ഭവം:=0 ഡാറ്റ അറേയുടെ തുടക്കം - ആദ്യം മുതൽ എണ്ണുന്നു

ഐ:=1..6 അറേയിലെ മൂലകങ്ങളുടെ എണ്ണം

പരീക്ഷണാത്മക ഡാറ്റ രണ്ട് വെക്റ്ററുകളായി ക്രമീകരിച്ചിരിക്കുന്നു

ബിൽറ്റ്-ഇൻ MathCad ഫംഗ്‌ഷനുകൾ ഉപയോഗിച്ച് നമുക്ക് ഇന്റർപോളേഷൻ നടത്താം

ലീനിയർ ഇന്റർപോളേഷൻ

Lf(x i):=linterp(x,y,x)

ക്യൂബിക് പൈൻ ഇന്റർപോളേഷൻ

CS:=cspline(x,y)

പരീക്ഷണാത്മക ഡാറ്റ ഉപയോഗിച്ച് ഒരു ക്യൂബിക് സ്പ്ലൈൻ നിർമ്മിക്കുന്നു

Lf(x i):=linterp(x,y,x i)

ബി-സ്പ്ലൈൻ ഇന്റർപോളേഷൻ

ഇന്റർപോളേഷൻ ക്രമം സജ്ജമാക്കുക. വെക്‌ടറിനേക്കാൾ (n-1) വെക്‌ടറിനേക്കാൾ കുറച്ച് ഘടകങ്ങൾ ഉണ്ടായിരിക്കണം x, കൂടാതെ ആദ്യത്തെ ഘടകം ആദ്യ മൂലകത്തേക്കാൾ കുറവോ തുല്യമോ ആയിരിക്കണം x, അവസാനത്തേത് x-ന്റെ അവസാന ഘടകത്തേക്കാൾ വലുതോ തുല്യമോ ആണ്.

BS:=bspline(x,y,u,n)

പരീക്ഷണാത്മക ഡാറ്റയെ അടിസ്ഥാനമാക്കി ഞങ്ങൾ ഒരു ബി-സ്പ്ലൈൻ നിർമ്മിക്കുന്നു

BSf(x i):=(BS, x,y,x i)

ഒരു ഏകോപന തലത്തിൽ ഞങ്ങൾ എല്ലാ ഏകദേശ പ്രവർത്തനങ്ങളുടെയും ഒരു ഗ്രാഫ് നിർമ്മിക്കുന്നു.

ചിത്രം 4.1-ഒരു കോർഡിനേറ്റ് പ്ലെയിനിലെ എല്ലാ ഏകദേശ പ്രവർത്തനങ്ങളുടെയും ഗ്രാഫ്.

ഉപസംഹാരം

കമ്പ്യൂട്ടേഷണൽ മാത്തമാറ്റിക്സിൽ, ഫംഗ്ഷനുകളുടെ ഇന്റർപോളേഷൻ ഒരു പ്രധാന പങ്ക് വഹിക്കുന്നു, അതായത്. തന്നിരിക്കുന്ന ഫംഗ്‌ഷൻ ഉപയോഗിച്ച്, മറ്റൊരു (സാധാരണയായി ലളിതമായ) ഫംഗ്‌ഷൻ നിർമ്മിക്കുന്നു, അതിന്റെ മൂല്യങ്ങൾ ഒരു നിശ്ചിത എണ്ണം പോയിന്റുകളിൽ നൽകിയിരിക്കുന്ന ഫംഗ്‌ഷന്റെ മൂല്യങ്ങളുമായി പൊരുത്തപ്പെടുന്നു. മാത്രമല്ല, ഇന്റർപോളേഷന് പ്രായോഗികവും സൈദ്ധാന്തികവുമായ പ്രാധാന്യമുണ്ട്. പ്രായോഗികമായി, ഒരു തുടർച്ചയായ ഫംഗ്ഷൻ അതിന്റെ ടാബുലേറ്റഡ് മൂല്യങ്ങളിൽ നിന്ന് പുനർനിർമ്മിക്കുന്നതിൽ പലപ്പോഴും പ്രശ്നം ഉയർന്നുവരുന്നു, ഉദാഹരണത്തിന്, ചില പരീക്ഷണങ്ങളിൽ നിന്ന് ലഭിച്ചതാണ്. പല ഫംഗ്ഷനുകളും വിലയിരുത്തുന്നതിന്, പോളിനോമിയലുകൾ അല്ലെങ്കിൽ ഫ്രാക്ഷണൽ റേഷണൽ ഫംഗ്ഷനുകൾ ഉപയോഗിച്ച് അവയെ ഏകദേശമാക്കുന്നത് ഫലപ്രദമാണെന്ന് ഇത് മാറുന്നു. ഡിഫറൻഷ്യൽ, ഇന്റഗ്രൽ സമവാക്യങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള രീതികൾ നേടുന്നതിന്, സംഖ്യാ സംയോജനത്തിനായുള്ള ക്വാഡ്രേച്ചർ ഫോർമുലകളുടെ നിർമ്മാണത്തിലും പഠനത്തിലും ഇന്റർപോളേഷൻ സിദ്ധാന്തം ഉപയോഗിക്കുന്നു. പോളിനോമിയൽ ഇന്റർപോളേഷന്റെ പ്രധാന പോരായ്മ, ഏറ്റവും സൗകര്യപ്രദവും സാധാരണയായി ഉപയോഗിക്കുന്നതുമായ ഗ്രിഡുകളിൽ ഒന്നിൽ ഇത് അസ്ഥിരമാണ് എന്നതാണ് - സമദൂര നോഡുകളുള്ള ഗ്രിഡ്. ചുമതല അനുവദിക്കുകയാണെങ്കിൽ, ചെബിഷെവ് നോഡുകളുള്ള ഒരു മെഷ് തിരഞ്ഞെടുത്ത് ഈ പ്രശ്നം പരിഹരിക്കാൻ കഴിയും. നമുക്ക് സ്വതന്ത്രമായി ഇന്റർപോളേഷൻ നോഡുകൾ തിരഞ്ഞെടുക്കാൻ കഴിയുന്നില്ലെങ്കിലോ നോഡുകൾ തിരഞ്ഞെടുക്കുന്നതിൽ കൂടുതൽ ആവശ്യപ്പെടാത്ത ഒരു അൽഗോരിതം ആവശ്യമാണെങ്കിൽ, യുക്തിസഹമായ ഇന്റർപോളേഷൻ പോളിനോമിയൽ ഇന്റർപോളേഷന് അനുയോജ്യമായ ഒരു ബദലായിരിക്കാം.

സ്പ്ലൈൻ ഇന്റർപോളേഷന്റെ ഗുണങ്ങളിൽ കമ്പ്യൂട്ടേഷണൽ അൽഗോരിതത്തിന്റെ ഉയർന്ന പ്രോസസ്സിംഗ് സ്പീഡ് ഉൾപ്പെടുന്നു, കാരണം ഒരു സ്പ്ലൈൻ ഒരു പീസ്വൈസ് പോളിനോമിയൽ ഫംഗ്ഷൻ ആയതിനാൽ, ഇന്റർപോളേഷൻ സമയത്ത്, പരിഗണിക്കപ്പെടുന്ന ശകലത്തിൽ ഉൾപ്പെടുന്ന ചെറിയ അളവിലുള്ള അളവെടുപ്പ് പോയിന്റുകൾക്കായി ഡാറ്റ ഒരേസമയം പ്രോസസ്സ് ചെയ്യുന്നു. ഈ നിമിഷം. ഇന്റർപോളേറ്റഡ് ഉപരിതലം സ്പേഷ്യൽ വേരിയബിളിറ്റി വിവരിക്കുന്നു വിവിധ സ്കെയിലുകൾഅതേ സമയം മിനുസമാർന്നതാണ്. പിന്നീടുള്ള സാഹചര്യം, വിശകലന നടപടിക്രമങ്ങൾ ഉപയോഗിച്ച് ഉപരിതലത്തിന്റെ ജ്യാമിതിയും ടോപ്പോളജിയും നേരിട്ട് വിശകലനം ചെയ്യുന്നത് സാധ്യമാക്കുന്നു.

ഈ പദത്തിന് മറ്റ് അർത്ഥങ്ങളുണ്ട്, ഇന്റർപോളേഷൻ കാണുക. പ്രവർത്തനത്തെക്കുറിച്ച്, കാണുക: ഇന്റർപോളന്റ്.

ഇന്റർപോളേഷൻ, ഇന്റർപോളേഷൻ (നിന്ന് lat. ഇന്റർ-പോലീസ് - « മിനുസപ്പെടുത്തിയ, പുതുക്കിയ, പുതുക്കിയ; പരിവർത്തനം ചെയ്തു") - കമ്പ്യൂട്ടേഷണൽ ഗണിതശാസ്ത്രത്തിൽ, അറിയപ്പെടുന്ന മൂല്യങ്ങളുടെ നിലവിലുള്ള ഒരു പ്രത്യേക കൂട്ടത്തിൽ നിന്ന് ഒരു അളവിന്റെ ഇന്റർമീഡിയറ്റ് മൂല്യങ്ങൾ കണ്ടെത്തുന്നതിനുള്ള ഒരു രീതി. "ഇന്റർപോളേഷൻ" എന്ന പദം ആദ്യമായി ജോൺ വാലിസ് തന്റെ "ദ അരിത്മെറ്റിക് ഓഫ് ദി ഇൻഫിനിറ്റ്" (1656) എന്ന ഗ്രന്ഥത്തിൽ ഉപയോഗിച്ചു.

പ്രവർത്തനപരമായ വിശകലനത്തിൽ, ഇന്റർപോളേഷൻ ലീനിയർ ഓപ്പറേറ്റർമാർഒരു പ്രത്യേക വിഭാഗത്തിന്റെ ഘടകങ്ങളായി ബനാച്ച് സ്പെയ്സുകളെ പരിഗണിക്കുന്ന ഒരു വിഭാഗമാണ്.

ശാസ്ത്രീയമായും അഭിമുഖീകരിക്കുന്നവരിൽ പലരും എഞ്ചിനീയറിംഗ് കണക്കുകൂട്ടലുകൾ, നിങ്ങൾ പലപ്പോഴും പരീക്ഷണാടിസ്ഥാനത്തിലോ രീതിയിലോ ലഭിച്ച മൂല്യങ്ങളുടെ സെറ്റ് ഉപയോഗിച്ച് പ്രവർത്തിക്കേണ്ടതുണ്ട് ക്രമരഹിത സാമ്പിൾ. ചട്ടം പോലെ, ഈ സെറ്റുകളെ അടിസ്ഥാനമാക്കി, ഒരു ഫംഗ്ഷൻ നിർമ്മിക്കേണ്ടത് ആവശ്യമാണ് ഉയർന്ന കൃത്യതഫലമായുണ്ടാകുന്ന മറ്റ് മൂല്യങ്ങൾ അടിക്കുക. ഈ പ്രശ്നത്തെ ഏകദേശം എന്ന് വിളിക്കുന്നു. ഇന്റർപോളേഷൻ എന്നത് ഒരു തരം ഏകദേശമാണ്, അതിൽ നിർമ്മിച്ച ഫംഗ്‌ഷന്റെ വക്രം ലഭ്യമായ ഡാറ്റ പോയിന്റുകളിലൂടെ കൃത്യമായി കടന്നുപോകുന്നു.

ഇന്റർപോളേഷനോട് അടുത്ത് ഒരു ടാസ്ക്ക് കൂടിയുണ്ട്, ചിലത് ഏകദേശമാക്കുന്നതിൽ ഉൾപ്പെടുന്നു സങ്കീർണ്ണമായ പ്രവർത്തനംമറ്റൊരു, ലളിതമായ പ്രവർത്തനം. ഒരു നിശ്ചിത ഫംഗ്‌ഷൻ ഉൽ‌പാദനപരമായ കണക്കുകൂട്ടലുകൾക്ക് വളരെ സങ്കീർണ്ണമാണെങ്കിൽ, നിങ്ങൾക്ക് അതിന്റെ മൂല്യം നിരവധി പോയിന്റുകളിൽ കണക്കാക്കാൻ ശ്രമിക്കാം, അവയിൽ നിന്ന് നിർമ്മിക്കുക, അതായത്, ഇന്റർപോളേറ്റ്, കൂടുതൽ ലളിതമായ പ്രവർത്തനം. തീർച്ചയായും, ലളിതമായ ഒരു ഫംഗ്‌ഷൻ ഉപയോഗിക്കുന്നത് യഥാർത്ഥ ഫംഗ്‌ഷൻ പോലെ കൃത്യമായ ഫലങ്ങൾ നൽകില്ല. എന്നാൽ ചില ക്ലാസുകളിലെ പ്രശ്‌നങ്ങളിൽ, കണക്കുകൂട്ടലുകളുടെ ലാളിത്യത്തിലും വേഗതയിലും നേടിയ നേട്ടം ഫലങ്ങളിൽ ഉണ്ടാകുന്ന പിശകിനെ മറികടക്കും.

ഓപ്പറേറ്റർ ഇന്റർപോളേഷൻ എന്നറിയപ്പെടുന്ന തികച്ചും വ്യത്യസ്തമായ ഒരു ഗണിത ഇന്റർപോളേഷനും എടുത്തുപറയേണ്ടതാണ്. TO ക്ലാസിക്കൽ കൃതികൾഓപ്പറേറ്റർമാരുടെ ഇന്റർപോളേഷനിൽ റൈസ്-തോറിൻ സിദ്ധാന്തവും മാർസിങ്കിവിച്ച് സിദ്ധാന്തവും ഉൾപ്പെടുന്നു, അവ മറ്റ് പല കൃതികൾക്കും അടിസ്ഥാനമാണ്.

നിർവചനങ്ങൾ

ചില പ്രദേശങ്ങളിൽ നിന്ന് x i (\displaystyle x_(i)) (i ∈ 0 , 1 , … , N (\ displaystyle i\in (0,1,\dots ,N))) യോജിപ്പില്ലാത്ത പോയിന്റുകളുടെ ഒരു സിസ്റ്റം പരിഗണിക്കുക ( \displaystyle D) . ഫംഗ്‌ഷന്റെ മൂല്യങ്ങൾ (\ഡിസ്‌പ്ലേസ്റ്റൈൽ എഫ്) ഈ പോയിന്റുകളിൽ മാത്രം അറിയാൻ അനുവദിക്കുക:

Y i = f (x i) , i = 1 , … , N . (\displaystyle y_(i)=f(x_(i)),\quad i=1,\ldots ,N.)

ഇന്റർപോളേഷൻ പ്രശ്നം ഒരു ഫംഗ്ഷൻ F (\displaystyle F) ഫംഗ്‌ഷനുകളുടെ ഒരു നിശ്ചിത ക്ലാസിൽ നിന്ന് കണ്ടെത്തുന്നതാണ്.

F (x i) = y i, i = 1, ..., N. (\displaystyle F(x_(i))=y_(i),\quad i=1,\ldots ,N.)

പോയിന്റുകൾ x i (\displaystyle x_(i)) എന്ന് വിളിക്കുന്നു ഇന്റർപോളേഷൻ നോഡുകൾ, അവയുടെ ആകെത്തുക ഇന്റർപോളേഷൻ ഗ്രിഡ്.
ജോഡികൾ (x i , y i) (\displaystyle (x_(i),y_(i))) എന്ന് വിളിക്കുന്നു ഡാറ്റ പോയിന്റുകൾഅഥവാ അടിസ്ഥാന പോയിന്റുകൾ.
"അയൽക്കാരൻ" മൂല്യങ്ങൾ തമ്മിലുള്ള വ്യത്യാസം Δ x i = x i - x i - 1 (\ displaystyle \Delta x_(i)=x_(i)-x_(i-1)) - ഇന്റർപോളേഷൻ ഗ്രിഡ് ഘട്ടം. ഇത് ഒന്നുകിൽ വേരിയബിളോ സ്ഥിരമോ ആകാം.
ഫംഗ്ഷൻ F (x) (\ഡിസ്പ്ലേസ്റ്റൈൽ F(x)) - ഇന്റർപോളിംഗ് പ്രവർത്തനംഅഥവാ ഇന്റർപോളന്റ്.

ഉദാഹരണം

1. താഴെ വിവരിച്ചിരിക്കുന്നതുപോലുള്ള ഒരു ടേബിൾ ഫംഗ്‌ഷൻ നമുക്കുണ്ടാകട്ടെ, അത് x (\displaystyle x) ന്റെ നിരവധി മൂല്യങ്ങൾക്ക് f (\displaystyle f) ന്റെ അനുബന്ധ മൂല്യങ്ങൾ നിർണ്ണയിക്കുന്നു:

X (\displaystyle x) f (x) (\displaystyle f(x))


0
1	0,8415
2	0,9093
3	0,1411
4	−0,7568
5	−0,9589
6	−0,2794

നിർദ്ദിഷ്ട പോയിന്റുകൾ ഒഴികെയുള്ള ഒരു പോയിന്റിൽ അത്തരം ഫംഗ്‌ഷന് എന്ത് മൂല്യമുണ്ടെന്ന് അറിയാൻ ഇന്റർപോളേഷൻ നമ്മെ സഹായിക്കുന്നു (ഉദാഹരണത്തിന്, എപ്പോൾ x = 2,5).

ഇപ്പോൾ ധാരാളം ഉണ്ട് പലവിധത്തിൽഇന്റർപോളേഷൻ. ഏറ്റവും അനുയോജ്യമായ അൽഗോരിതം തിരഞ്ഞെടുക്കുന്നത് ചോദ്യങ്ങൾക്കുള്ള ഉത്തരങ്ങളെ ആശ്രയിച്ചിരിക്കുന്നു: തിരഞ്ഞെടുത്ത രീതി എത്ര കൃത്യമാണ്, അത് ഉപയോഗിക്കുന്നതിനുള്ള ചെലവ് എന്താണ്, ഇന്റർപോളേഷൻ പ്രവർത്തനം എത്ര സുഗമമാണ്, അതിന് എത്ര ഡാറ്റ പോയിന്റുകൾ ആവശ്യമാണ്, മുതലായവ.

2. ഇന്റർമീഡിയറ്റ് മൂല്യം കണ്ടെത്തുക (ലീനിയർ ഇന്റർപോളേഷൻ വഴി).

6000	15.5
6378	?
8000	19.2

15.5 + (6378 - 6000) 8000 - 6000 ∗ (19.2 - 15.5) 1 = 16.1993 (\ ഡിസ്പ്ലേ സ്റ്റൈൽ ?=15.5+(\frac ((6378-6000)-(6378-6000)) (2000) 15.5))(1))=16.1993)

പ്രോഗ്രാമിംഗ് ഭാഷകളിൽ

y = 3 x + x 2 (\displaystyle y=3x+x^(2)) ഫംഗ്‌ഷനുള്ള ലീനിയർ ഇന്റർപോളേഷന്റെ ഒരു ഉദാഹരണം. ഉപയോക്താവിന് 1 മുതൽ 10 വരെയുള്ള ഒരു നമ്പർ നൽകാം.

ഫോർട്രാൻ

പ്രോഗ്രാം interpol integer i real x, y, xv, yv, yv2 അളവ് x(10) അളവ് y(10) കോൾ prisv(x, i) call func(x, y, i) write(*,*) "നമ്പർ നൽകുക: "വായിക്കുക(*,*) xv എങ്കിൽ ((xv >= 1).and.(xv xv)) തുടർന്ന് yv2 = ((xv - x(i)) * (y(i+1) - y(i)) / (x(i+1) - x(i))) + y(i) end if end do end subroutine

C++

int main() ( system("COLOR 0A"); double ob, x1, x2, y1, y2, p1, p2, pi, skolko, status; system("echo Interpolation X1 - X2 "); system("echo Enter നമ്പർ: "); cin >> ob; സിസ്റ്റം("എക്കോ ഉദാഹരണത്തിന് 62, C1 = 60, L1 = 1.31, C2 = 80, L2 = 1.29"); cout > x1; cout > x2; cout > y1; cout > y2 ; p1 = y1 - x1; p2 = y2 - x2; pi = p2 / p1; skolko = ob - x1; സ്റ്റാറ്റസ് = x2 + (pi * skolko); cout

ഇന്റർപോളേഷൻ രീതികൾ

അടുത്തുള്ള അയൽക്കാരന്റെ ഇന്റർപോളേഷൻ

ഇന്റർപോളേഷന്റെ ഏറ്റവും ലളിതമായ രീതി അടുത്തുള്ള അയൽക്കാരന്റെ ഇന്റർപോളേഷൻ രീതിയാണ്.

ബഹുപദങ്ങൾ വഴിയുള്ള ഇന്റർപോളേഷൻ

പ്രായോഗികമായി, പോളിനോമിയലുകൾ ഉപയോഗിച്ചുള്ള ഇന്റർപോളേഷൻ മിക്കപ്പോഴും ഉപയോഗിക്കുന്നു. പോളിനോമിയലുകൾ കണക്കുകൂട്ടാൻ എളുപ്പമാണ്, അവയുടെ ഡെറിവേറ്റീവുകൾ വിശകലനപരമായി കണ്ടെത്താൻ എളുപ്പമാണ്, തുടർച്ചയായ പ്രവർത്തനങ്ങളുടെ ഇടത്തിൽ ബഹുപദങ്ങളുടെ കൂട്ടം സാന്ദ്രമാണ് (വെയർസ്ട്രാസ് സിദ്ധാന്തം) എന്നിവയാണ് ഇതിന് പ്രാഥമികമായി കാരണം.

ലീനിയർ ഇന്റർപോളേഷൻ
ന്യൂട്ടന്റെ ഇന്റർപോളേഷൻ ഫോർമുല
പരിമിതമായ വ്യത്യാസ രീതി
IMN-1, IMN-2
ലഗ്രാഞ്ച് പോളിനോമിയൽ (ഇന്റർപോളേഷൻ പോളിനോമിയൽ)
Aitken പദ്ധതി
സ്പ്ലൈൻ പ്രവർത്തനം
ക്യൂബിക് സ്പ്ലൈൻ

വിപരീത ഇന്റർപോളേഷൻ (എക്സ് കൊടുത്തിരിക്കുന്ന y കണക്കാക്കുന്നു)

ലഗ്രാഞ്ച് പോളിനോമിയൽ
ന്യൂട്ടന്റെ ഫോർമുല ഉപയോഗിച്ച് റിവേഴ്സ് ഇന്റർപോളേഷൻ
ഗാസ് ഫോർമുല ഉപയോഗിച്ച് വിപരീത ഇന്റർപോളേഷൻ

നിരവധി വേരിയബിളുകളുടെ ഒരു പ്രവർത്തനത്തിന്റെ ഇന്റർപോളേഷൻ

ബിലീനിയർ ഇന്റർപോളേഷൻ
ബിക്യൂബിക് ഇന്റർപോളേഷൻ

മറ്റ് ഇന്റർപോളേഷൻ രീതികൾ

യുക്തിസഹമായ ഇന്റർപോളേഷൻ
ത്രികോണമിതി ഇന്റർപോളേഷൻ

ബന്ധപ്പെട്ട ആശയങ്ങൾ

എക്സ്ട്രാപോളേഷൻ - പുറത്ത് പോയിന്റുകൾ കണ്ടെത്തുന്നതിനുള്ള രീതികൾ നിർദ്ദിഷ്ട ഇടവേള(കർവ് വിപുലീകരണം)
ഏകദേശം - ഏകദേശ വളവുകൾ നിർമ്മിക്കുന്നതിനുള്ള രീതികൾ

വിപരീത ഇന്റർപോളേഷൻ

സ്‌പെയ്‌സ് C2-ൽ നിന്നുള്ള ഫംഗ്‌ഷനുകളുടെ ക്ലാസിൽ ഗ്രാഫുകൾ അറേയുടെ പോയിന്റുകളിലൂടെ കടന്നുപോകുന്നു (xi, yi), i = 0, 1, . . . , എം.

പരിഹാരം. റഫറൻസ് പോയിന്റുകളിലൂടെ കടന്നുപോകുന്ന എല്ലാ ഫംഗ്‌ഷനുകളിലും (xi, f(xi)) സൂചിപ്പിച്ച സ്‌പെയ്‌സിൽ പെടുന്നു, ഇത് ക്യൂബിക് സ്‌പ്ലൈൻ S(x) ആണ്, ഇത് S00(a) = S00(b) = 0 എന്ന അതിർത്തി വ്യവസ്ഥകളെ തൃപ്തിപ്പെടുത്തുന്നു. , അത് എക്സ്ട്രീം (മിനിമം) ഫങ്ഷണൽ I(f) നൽകുന്നു.

പലപ്പോഴും പ്രായോഗികമായി, ഒരു ഫംഗ്ഷന്റെ തന്നിരിക്കുന്ന മൂല്യം ഉപയോഗിച്ച് ഒരു ആർഗ്യുമെന്റിന്റെ മൂല്യം തിരയുന്നതിലാണ് പ്രശ്നം ഉണ്ടാകുന്നത്. വിപരീത ഇന്റർപോളേഷൻ രീതികൾ ഉപയോഗിച്ചാണ് ഈ പ്രശ്നം പരിഹരിക്കുന്നത്. എങ്കിൽ നൽകിയ പ്രവർത്തനംമോണോടോണിക് ആണ്, പിന്നെ റിവേഴ്സ് ഇന്റർപോളേഷൻ ഫംഗ്ഷനെ ഒരു ആർഗ്യുമെന്റ് ഉപയോഗിച്ച് മാറ്റിസ്ഥാപിക്കുന്നതിലൂടെയും പിന്നീട് ഇന്റർപോളേറ്റ് ചെയ്യുന്നതിലൂടെയും വളരെ എളുപ്പത്തിൽ നിർവ്വഹിക്കുന്നു. നൽകിയിരിക്കുന്ന പ്രവർത്തനം ഏകതാനമല്ലെങ്കിൽ, ഈ സാങ്കേതികവിദ്യ ഉപയോഗിക്കാൻ കഴിയില്ല. തുടർന്ന്, ഫംഗ്ഷന്റെയും വാദത്തിന്റെയും റോളുകൾ മാറ്റാതെ, ഞങ്ങൾ ഒന്നോ അല്ലെങ്കിൽ മറ്റൊരു ഇന്റർപോളേഷൻ ഫോർമുല എഴുതുന്നു; ആർഗ്യുമെന്റിന്റെ അറിയപ്പെടുന്ന മൂല്യങ്ങൾ ഉപയോഗിച്ച്, ഫംഗ്ഷൻ അറിയാമെന്ന് കരുതി, തത്ഫലമായുണ്ടാകുന്ന സമവാക്യം ആർഗ്യുമെന്റുമായി ബന്ധപ്പെട്ട് ഞങ്ങൾ പരിഹരിക്കുന്നു.

ആദ്യ സാങ്കേതികത ഉപയോഗിക്കുമ്പോൾ ശേഷിക്കുന്ന പദത്തിന്റെ മൂല്യനിർണ്ണയം നേരിട്ടുള്ള ഇന്റർപോളേഷൻ പോലെയായിരിക്കും, നേരിട്ടുള്ള പ്രവർത്തനത്തിന്റെ ഡെറിവേറ്റീവുകൾ മാത്രം ഡെറിവേറ്റീവുകൾ ഉപയോഗിച്ച് മാറ്റിസ്ഥാപിക്കേണ്ടതുണ്ട്. വിപരീത പ്രവർത്തനം. രണ്ടാമത്തെ രീതിയുടെ പിശക് നമുക്ക് കണക്കാക്കാം. നമുക്ക് ഒരു ഫംഗ്ഷൻ നൽകിയിട്ടുണ്ടെങ്കിൽ f(x) കൂടാതെ Ln (x) എന്നത് x0, x1, x2, എന്നീ നോഡുകളിൽ നിന്ന് ഈ ഫംഗ്‌ഷനുവേണ്ടി നിർമ്മിച്ച ഒരു Lagrange ഇന്റർപോളേഷൻ പോളിനോമിയലാണ്. . . , xn, പിന്നെ

f (x) - Ln (x) =(n + 1)! (x− x0) . . . (x− xn) .

f (¯x) = y¯ (y¯ നൽകിയിരിക്കുന്നു) x¯ ന്റെ മൂല്യം കണ്ടെത്തേണ്ടതുണ്ടെന്ന് കരുതുക. നമ്മൾ Ln (x) = y¯ എന്ന സമവാക്യം പരിഹരിക്കും. നമുക്ക് കുറച്ച് മൂല്യം x¯ നേടാം. മുമ്പത്തെ സമവാക്യത്തിന് പകരമായി, നമുക്ക് ലഭിക്കുന്നത്:

Mn+1


f (x¯) - Ln (x¯) = f (x¯) - y¯ = f (x¯) - f (¯x) =
f (x¯) - Ln (x¯) = f (x¯) - y¯ = f (x¯) - f (¯x) =
ലാങ്‌റേഞ്ചിന്റെ ഫോർമുല പ്രയോഗിക്കുമ്പോൾ, നമുക്ക് ലഭിക്കും
(x¯ - x¯) f0 (η) =


ഇവിടെ η x¯ നും x¯ നും ഇടയിലാണ്. x¯ ഉം x¯ ഉം മിനിറ്റും അടങ്ങുന്ന ഒരു ഇടവേള ആണെങ്കിൽ

അവസാന പദപ്രയോഗത്തിൽ നിന്ന് ഇത് ഇപ്രകാരമാണ്:

|x¯ - x¯| 6m1(n+1)! |$n(x¯)| .

ഈ സാഹചര്യത്തിൽ, തീർച്ചയായും, നമ്മൾ Ln (x) = y¯ എന്ന സമവാക്യം കൃത്യമായി പരിഹരിച്ചതായി അനുമാനിക്കപ്പെടുന്നു.

പട്ടികകൾ സൃഷ്ടിക്കാൻ ഇന്റർപോളേഷൻ ഉപയോഗിക്കുന്നു

ഫംഗ്‌ഷനുകളുടെ പട്ടികകളുടെ സമാഹാരത്തിൽ ഇന്റർപോളേഷൻ സിദ്ധാന്തത്തിന് പ്രയോഗങ്ങളുണ്ട്. അത്തരമൊരു പ്രശ്നം ലഭിച്ചതിനാൽ, കണക്കുകൂട്ടലുകൾ ആരംഭിക്കുന്നതിന് മുമ്പ് ഗണിതശാസ്ത്രജ്ഞൻ നിരവധി ചോദ്യങ്ങൾ പരിഹരിക്കേണ്ടതുണ്ട്. കണക്കുകൂട്ടലുകൾ നടപ്പിലാക്കുന്ന ഒരു ഫോർമുല തിരഞ്ഞെടുക്കണം. ഓരോ സൈറ്റിനും ഈ ഫോർമുല വ്യത്യാസപ്പെടാം. സാധാരണഗതിയിൽ, ഫംഗ്‌ഷൻ മൂല്യങ്ങൾ കണക്കാക്കുന്നതിനുള്ള സൂത്രവാക്യങ്ങൾ ബുദ്ധിമുട്ടുള്ളതാണ്, അതിനാൽ അവ ചില റഫറൻസ് മൂല്യങ്ങൾ നേടുന്നതിന് ഉപയോഗിക്കുന്നു, തുടർന്ന് ഉപടാബുലേഷൻ വഴി പട്ടിക ഘനീഭവിക്കുന്നു. ഫംഗ്‌ഷന്റെ റഫറൻസ് മൂല്യങ്ങൾ നൽകുന്ന ഫോർമുല ഇനിപ്പറയുന്ന ഉപടാബുലേഷൻ കണക്കിലെടുത്ത് പട്ടികകളുടെ ആവശ്യമായ കൃത്യത നൽകണം. സ്ഥിരമായ ഒരു ഘട്ടം ഉപയോഗിച്ച് നിങ്ങൾക്ക് പട്ടികകൾ സൃഷ്ടിക്കണമെങ്കിൽ, നിങ്ങൾ ആദ്യം അതിന്റെ ഘട്ടം നിർണ്ണയിക്കേണ്ടതുണ്ട്.

ബാക്ക് ഫസ്റ്റ് പ്രിവിയസ് അടുത്ത ലാസ്റ്റ് ഗോ വിഷയ സൂചിക

മിക്കപ്പോഴും, ഫംഗ്‌ഷൻ ടേബിളുകൾ കംപൈൽ ചെയ്യപ്പെടുന്നതിനാൽ ലീനിയർ ഇന്റർപോളേഷൻ സാധ്യമാണ് (അതായത്, ടെയ്‌ലർ ഫോർമുലയുടെ ആദ്യ രണ്ട് പദങ്ങൾ ഉപയോഗിച്ച് ഇന്റർപോളേഷൻ). ഈ സാഹചര്യത്തിൽ, ശേഷിക്കുന്ന പദത്തിന് ഫോം ഉണ്ടായിരിക്കും

R1 (x) =f00 (ξ)h2t(t - 1).

ഇവിടെ ξ എന്നത് ആർഗ്യുമെന്റിന്റെ അടുത്തുള്ള രണ്ട് പട്ടിക മൂല്യങ്ങൾക്കിടയിലുള്ള ഇടവേളയാണ്, അതിൽ x സ്ഥിതിചെയ്യുന്നു, കൂടാതെ t 0 നും 1 നും ഇടയിലാണ്. ഉൽപ്പന്നം t (t - 1) ഏറ്റവും വലിയ മൊഡ്യൂളോ എടുക്കുന്നു.

മൂല്യം t = 12. ഈ മൂല്യം 14 ആണ്. അതിനാൽ,

ഈ പിശകിനൊപ്പം - രീതിയുടെ പിശക് - ഇന്റർമീഡിയറ്റ് മൂല്യങ്ങളുടെ പ്രായോഗിക കണക്കുകൂട്ടലിൽ, മാറ്റാനാവാത്ത പിശകും റൗണ്ടിംഗ് പിശകും ഉണ്ടാകുമെന്ന് ഓർമ്മിക്കേണ്ടതാണ്. നമ്മൾ നേരത്തെ കണ്ടതുപോലെ, ലീനിയർ ഇന്റർപോളേഷനിലെ മാരകമായ പിശക് ടാബുലേറ്റ് ചെയ്ത ഫംഗ്ഷൻ മൂല്യങ്ങളിലെ പിശകിന് തുല്യമായിരിക്കും. റൗണ്ടിംഗ് പിശക് ആശ്രയിച്ചിരിക്കും കമ്പ്യൂട്ടിംഗ് സൗകര്യങ്ങൾകണക്കുകൂട്ടൽ പ്രോഗ്രാമിൽ നിന്നും.

തിരികെ ആദ്യം മുമ്പത്തെ അടുത്തത് അവസാനം സൂചികയിലേക്ക് പോകുക

വിഷയ സൂചിക

രണ്ടാമത്തെ ക്രമത്തിന്റെ വേർതിരിച്ച വ്യത്യാസങ്ങൾ, 8 ആദ്യ ക്രമം, 8

സ്പ്ലൈൻ, 15

ഇന്റർപോളേഷൻ നോഡുകൾ, 4

തിരികെ ആദ്യം മുമ്പത്തെ അടുത്തത് അവസാനം സൂചികയിലേക്ക് പോകുക

/ Material_studentam_po_RGR_BZhD / ഇന്റർപോളേഷൻ എങ്ങനെ നടത്താം

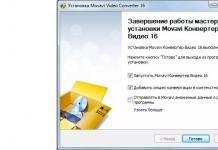
പട്ടിക ഡാറ്റ ഇന്റർപോളേറ്റ് ചെയ്യുന്നതിനുള്ള ഫോർമുല

വ്യവസ്ഥയിൽ നിന്ന് NHR (Q, t) ന്റെ അളവ് വരുമ്പോൾ, രണ്ടാമത്തെ പ്രവർത്തനത്തിൽ ഉപയോഗിച്ചു ഇടയ്ക്ക് ഇടനിലക്കാരനാണ് 100 ടി, 300 ടി.

(ഒഴിവാക്കൽ:വ്യവസ്ഥ പ്രകാരം Q 100 അല്ലെങ്കിൽ 300 ന് തുല്യമാണെങ്കിൽ, ഇന്റർപോളേഷൻ ആവശ്യമില്ല).

വൈ ഒ- താങ്കളുടെ യഥാർത്ഥ അളവ്അവസ്ഥയിൽ നിന്നുള്ള NHR, ടണ്ണിൽ

(Q എന്ന അക്ഷരവുമായി പൊരുത്തപ്പെടുന്നു)

വൈ 1 – ചെറുത്

(പട്ടിക 11-16 മുതൽ, സാധാരണയായി 100 ന് തുല്യമാണ്).

വൈ 2 – കൂടുതൽ നിങ്ങളുടേതിന് ഏറ്റവും അടുത്തുള്ള NHR അളവിന്റെ മൂല്യം, ടണ്ണിൽ

(പട്ടിക 11-16 മുതൽ, സാധാരണയായി 300 ന് തുല്യമാണ്).

x 1 വൈ 1 (x 1 എതിർവശത്ത് സ്ഥിതിചെയ്യുന്നു വൈ 1 ), കി.മീ.

x 2 - യഥാക്രമം മലിനമായ വായുവിന്റെ (Gt) വിതരണത്തിന്റെ ആഴത്തിന്റെ പട്ടിക മൂല്യം വൈ 2 (x 2 എതിർവശത്ത് സ്ഥിതിചെയ്യുന്നു വൈ 2 ), കി.മീ.

x 0 - ആവശ്യമായ മൂല്യം ജി ടിഉചിതമായ വൈ ഒ(സൂത്രം അനുസരിച്ച്).

ഉദാഹരണം.

NHR - ക്ലോറിൻ; Q = 120 ടി;

എസ്.വി.എസ്.പിയുടെ തരം (ലംബമായ വായു പ്രതിരോധത്തിന്റെ ഡിഗ്രി) - വിപരീതം.

കണ്ടെത്തുക ജി ടി- മലിനമായ വായുവിന്റെ ഒരു മേഘത്തിന്റെ വിതരണത്തിന്റെ ആഴത്തിന്റെ പട്ടിക മൂല്യം.

ഞങ്ങൾ 11-16 പട്ടികകളിലൂടെ നോക്കുകയും നിങ്ങളുടെ അവസ്ഥയുമായി പൊരുത്തപ്പെടുന്ന ഡാറ്റ കണ്ടെത്തുകയും ചെയ്യുന്നു (ക്ലോറിൻ, വിപരീതം).

പട്ടിക 11 അനുയോജ്യമാണ്.

മൂല്യങ്ങൾ തിരഞ്ഞെടുക്കുന്നു വൈ 1 , വൈ 2, x 1 , x 2 . പ്രധാനപ്പെട്ടത് - കാറ്റിന്റെ വേഗത 1 m/s ആയും താപനില 20 °C ആയും എടുക്കുക.

ഞങ്ങൾ തിരഞ്ഞെടുത്ത മൂല്യങ്ങൾ ഫോർമുലയിലേക്ക് മാറ്റി കണ്ടെത്തുന്നു x 0 .

പ്രധാനപ്പെട്ടത് - എങ്കിൽ കണക്കുകൂട്ടൽ ശരിയാണ് x 0 ഇടയിൽ എവിടെയെങ്കിലും ഒരു മൂല്യമുണ്ടാകും x 1 , x 2 .

1.4 ലഗ്രാഞ്ച് ഇന്റർപോളേഷൻ ഫോർമുല

ഇന്റർപോളിംഗ് നിർമ്മിക്കുന്നതിന് ലഗ്രാഞ്ച് നിർദ്ദേശിച്ച അൽഗോരിതം

പട്ടികകളിൽ നിന്നുള്ള പ്രവർത്തനങ്ങൾ (1) രൂപത്തിൽ ഒരു ഇന്റർപോളേഷൻ പോളിനോമിയൽ Ln(x) നിർമ്മിക്കുന്നതിന് നൽകുന്നു

വ്യക്തമായും, (10) വ്യവസ്ഥകളുടെ (11) പൂർത്തീകരണം ഇന്റർപോളേഷൻ പ്രശ്നം സജ്ജീകരിക്കുന്നതിനുള്ള വ്യവസ്ഥകളുടെ (2) പൂർത്തീകരണം നിർണ്ണയിക്കുന്നു.

ലി(x) എന്ന ബഹുപദങ്ങൾ ഇങ്ങനെ എഴുതിയിരിക്കുന്നു

ഫോർമുലയുടെ ഡിനോമിനേറ്ററിൽ ഒരു ഘടകം പോലും ഇല്ല എന്നത് ശ്രദ്ധിക്കുക (14) പൂജ്യത്തിന് തുല്യം. സിഐ സ്ഥിരാങ്കങ്ങളുടെ മൂല്യങ്ങൾ കണക്കാക്കിയ ശേഷം, നൽകിയിരിക്കുന്ന പോയിന്റുകളിൽ ഇന്റർപോളേറ്റഡ് ഫംഗ്ഷന്റെ മൂല്യങ്ങൾ കണക്കാക്കാൻ നിങ്ങൾക്ക് അവ ഉപയോഗിക്കാം.

സൂത്രവാക്യങ്ങൾ (13), (14) എന്നിവ കണക്കിലെടുത്ത് ലഗ്രാഞ്ച് ഇന്റർപോളേഷൻ പോളിനോമിയലിന്റെ (11) ഫോർമുല ഇങ്ങനെ എഴുതാം

qi (x - x0)(x - x1) K (x - xi -1)(x - xi +1) K (x - xn)

1.4.1.Lagrange ഫോർമുല ഉപയോഗിച്ച് മാനുവൽ കണക്കുകൂട്ടലുകളുടെ ഓർഗനൈസേഷൻ

ലഗ്രാഞ്ച് ഫോർമുലയുടെ നേരിട്ടുള്ള പ്രയോഗം സമാനമായ നിരവധി കണക്കുകൂട്ടലുകളിലേക്ക് നയിക്കുന്നു. ചെറിയ വലിപ്പത്തിലുള്ള പട്ടികകൾക്കായി, ഈ കണക്കുകൂട്ടലുകൾ സ്വമേധയാ അല്ലെങ്കിൽ ഒരു പ്രോഗ്രാം പരിതസ്ഥിതിയിൽ നടത്താം

ആദ്യ ഘട്ടത്തിൽ, മാനുവൽ കണക്കുകൂട്ടലുകൾക്കുള്ള ഒരു അൽഗോരിതം ഞങ്ങൾ പരിഗണിക്കും. ഭാവിയിൽ, ഇതേ കണക്കുകൂട്ടലുകൾ പരിസ്ഥിതിയിൽ ആവർത്തിക്കണം

മൈക്രോസോഫ്റ്റ് എക്സൽഅല്ലെങ്കിൽ OpenOffice.org Calc.

ചിത്രത്തിൽ. നാല് നോഡുകൾ നിർവചിച്ചിരിക്കുന്ന ഇന്റർപോളേറ്റഡ് ഫംഗ്‌ഷന്റെ യഥാർത്ഥ പട്ടികയുടെ ഒരു ഉദാഹരണം ചിത്രം 6 കാണിക്കുന്നു.

ചിത്രം.6. ഇന്റർപോളേറ്റഡ് ഫംഗ്‌ഷന്റെ നാല് നോഡുകൾക്കുള്ള പ്രാരംഭ ഡാറ്റ അടങ്ങുന്ന പട്ടിക

പട്ടികയുടെ മൂന്നാമത്തെ നിരയിൽ, ഫോർമുലകൾ (14) ഉപയോഗിച്ച് കണക്കാക്കിയ ഗുണകങ്ങളുടെ qi മൂല്യങ്ങൾ ഞങ്ങൾ എഴുതുന്നു. n=3 എന്നതിനായുള്ള ഈ ഫോർമുലകളുടെ ഒരു റെക്കോർഡ് ചുവടെയുണ്ട്.

q0=Y0/(x0-x1)/(x0-x2)/(x0-x3)q1=Y1/(x1-x0)/(x1-x2)/(x1-x3)(16) q2=Y2/( x2-x0)/(x2-x1)/(x2-x3)q3=Y3/(x3-x0)/(x3-x1)/(x3-x2)

മാനുവൽ കണക്കുകൂട്ടലുകൾ നടപ്പിലാക്കുന്നതിനുള്ള അടുത്ത ഘട്ടം, ഫോർമുലകൾ (13) അനുസരിച്ച് നടപ്പിലാക്കുന്ന li(x) (j=0,1,2,3) മൂല്യങ്ങളുടെ കണക്കുകൂട്ടലാണ്.

ഞങ്ങൾ പരിഗണിക്കുന്ന നാല് നോഡുകളുള്ള പട്ടികയുടെ പതിപ്പിനായി ഈ ഫോർമുലകൾ എഴുതാം:

l0(x)=q0(x-x1)·(x-x2)·(x-x3),

l1(x)=q1(x-x0)·(x-x2)·(x-x3),

l2(x)=q2(x-x0)·(x-x1)·(x-x3),(17) l3(x)=q3(x-x0)·(x-x1)·(x-x2) .

ലി(xj) (j=0,1,2,3) എന്ന ബഹുപദങ്ങളുടെ മൂല്യങ്ങൾ കണക്കാക്കി പട്ടിക സെല്ലുകളിൽ എഴുതാം. ഫോർമുല (11) അനുസരിച്ച് Ycalc(x) എന്ന ഫംഗ്‌ഷന്റെ മൂല്യങ്ങൾ വരിയായി li (xj) മൂല്യങ്ങൾ സംഗ്രഹിച്ചതിന്റെ ഫലമായി ലഭിക്കും.

കണക്കാക്കിയ മൂല്യങ്ങളുടെ നിരകളും Ycalc(x) മൂല്യങ്ങളുടെ നിരയും ഉൾപ്പെടെ പട്ടികയുടെ ഫോർമാറ്റ് ചിത്രം 8-ൽ കാണിച്ചിരിക്കുന്നു.

അരി. 8. ആർഗ്യുമെന്റ് xi യുടെ എല്ലാ മൂല്യങ്ങൾക്കും ഫോർമുലകൾ (16), (17), (11) ഉപയോഗിച്ച് നടത്തിയ മാനുവൽ കണക്കുകൂട്ടലുകളുടെ ഫലങ്ങളുള്ള പട്ടിക

ചിത്രത്തിൽ കാണിച്ചിരിക്കുന്ന പട്ടിക സൃഷ്ടിച്ച ശേഷം. 8, ഫോർമുലകൾ (17), (11) എന്നിവ ഉപയോഗിച്ച് നിങ്ങൾക്ക് ആർഗ്യുമെന്റ് X ന്റെ ഏത് മൂല്യത്തിനും ഇന്റർപോളേറ്റഡ് ഫംഗ്‌ഷന്റെ മൂല്യം കണക്കാക്കാം. ഉദാഹരണത്തിന്, X=1 ന് ഞങ്ങൾ ലി(1) (i=0,) മൂല്യങ്ങൾ കണക്കാക്കുന്നു 1,2,3):

l0(1)= 0.7763; l1(1)= 3.5889; l2(1)=-1.5155;l3(1)= 0.2966.

li(1) ന്റെ മൂല്യങ്ങൾ സംഗ്രഹിച്ചാൽ നമുക്ക് Yinterp(1)=3.1463 മൂല്യം ലഭിക്കും.

1.4.2. മൈക്രോസോഫ്റ്റ് എക്സൽ പ്രോഗ്രാം പരിതസ്ഥിതിയിൽ ലാഗ്രാഞ്ച് ഫോർമുലകൾ ഉപയോഗിച്ച് ഒരു ഇന്റർപോളേഷൻ അൽഗോരിതം നടപ്പിലാക്കൽ

ഇൻറർപോളേഷൻ അൽഗോരിതം നടപ്പിലാക്കുന്നത്, മാനുവൽ കണക്കുകൂട്ടലുകൾ പോലെ, ചിത്രത്തിൽ qi എന്ന ഗുണകങ്ങൾ കണക്കാക്കുന്നതിനുള്ള സൂത്രവാക്യങ്ങൾ എഴുതുന്നതിലൂടെ ആരംഭിക്കുന്നു. 9 പട്ടിക നിരകൾ കാണിക്കുന്നു മൂല്യങ്ങൾ നൽകിയിരിക്കുന്നുആർഗ്യുമെന്റ്, ഇന്റർപോളേറ്റഡ് ഫംഗ്ഷൻ, ഗുണകങ്ങൾ ക്വി. ഈ പട്ടികയുടെ വലതുവശത്ത് C നിരയിലെ സെല്ലുകളിൽ എഴുതിയിരിക്കുന്ന സൂത്രവാക്യങ്ങൾ qi ഗുണകങ്ങളുടെ മൂല്യങ്ങൾ കണക്കാക്കുന്നു.

ВС2: "=B2/((A2-A3)*(A2-A4)*(A2-A5))" Ж q0

ВС3: "=B3/((A3-A4)*(A3-A5)*(A3-A2))" Ж q1

ВС4: "=B4/((A4-A5)*(A4-A2)*(A4-A3))" Ж q2

ВС5: "=B5/((A5-A2)*(A5-A3)*(A5-A4))" Ж q3

അരി. 9 ഗുണകങ്ങളുടെ പട്ടിക qi, കണക്കുകൂട്ടൽ സൂത്രവാക്യങ്ങൾ

സെൽ C2-ൽ q0 ഫോർമുല നൽകിയ ശേഷം, അത് C3 സെല്ലുകളിലൂടെ C5-ലേക്ക് നീട്ടുന്നു. അതിനുശേഷം ഈ സെല്ലുകളിലെ സൂത്രവാക്യങ്ങൾ ചിത്രത്തിൽ കാണിച്ചിരിക്കുന്ന ഫോമിന് (16) അനുസരിച്ച് ക്രമീകരിക്കുന്നു. 9.

Ycalc(xi),

ഫോർമുലകൾ (17) നടപ്പിലാക്കുമ്പോൾ, ഡി, ഇ, എഫ്, ജി എന്നീ നിരകളിലെ സെല്ലുകളിൽ li (x) (i=0,1,2,3) മൂല്യങ്ങൾ കണക്കാക്കുന്നതിനുള്ള സൂത്രവാക്യങ്ങൾ ഞങ്ങൾ എഴുതുന്നു. മൂല്യം കണക്കാക്കുന്നതിനായി സെൽ D2 ൽ l0(x0) ഞങ്ങൾ ഫോർമുല എഴുതുന്നു:

=$C$2*($A2-$A$3)*($A2-$A$4)*($A2-$A$5),

നമുക്ക് l0 (xi) (i=0,1,2,3) മൂല്യങ്ങൾ ലഭിക്കും.

Li(x0) (i=1,2,3) കണക്കാക്കുന്നതിനുള്ള കമ്പ്യൂട്ടേഷണൽ ഫോർമുലകൾ രൂപപ്പെടുത്തുന്നതിന് E, F, G നിരകളിലുടനീളം ഫോർമുല നീട്ടാൻ $A2 ലിങ്ക് ഫോർമാറ്റ് നിങ്ങളെ അനുവദിക്കുന്നു. നിങ്ങൾ ഒരു വരിയിൽ ഒരു ഫോർമുല വലിച്ചിടുമ്പോൾ, ആർഗ്യുമെന്റ് കോളത്തിന്റെ സൂചിക മാറില്ല. l0(x0) ഫോർമുല വരച്ചതിനുശേഷം li(x0) (i=1,2,3) കണക്കാക്കാൻ, ഫോർമുലകൾ (17) അനുസരിച്ച് അവ ശരിയാക്കേണ്ടത് ആവശ്യമാണ്.

H നിരയിൽ ഞങ്ങൾ സ്ഥാപിക്കുന്നു എക്സൽ ഫോർമുലകൾഫോർമുല ഉപയോഗിച്ച് li(x) സംഗ്രഹിക്കാൻ

(11)അൽഗരിതം.

ചിത്രത്തിൽ. പരിസ്ഥിതിയിൽ നടപ്പിലാക്കിയ ഒരു പട്ടിക ചിത്രം 10 കാണിക്കുന്നു മൈക്രോസോഫ്റ്റ് പ്രോഗ്രാമുകൾഎക്സൽ. പട്ടികയുടെ സെല്ലുകളിൽ എഴുതിയിരിക്കുന്ന സൂത്രവാക്യങ്ങളുടെ കൃത്യതയുടെ അടയാളവും നിർവഹിച്ച കമ്പ്യൂട്ടേഷണൽ പ്രവർത്തനങ്ങളും ഫലമായുണ്ടാകുന്ന ഡയഗണൽ മാട്രിക്സ് li(xj) (i=0,1,2,3),(j=0,1,2, 3), ചിത്രത്തിൽ കാണിച്ചിരിക്കുന്ന ഫലങ്ങൾ ആവർത്തിക്കുന്നു. 8, കൂടാതെ സോഴ്സ് ടേബിളിന്റെ നോഡുകളിലെ ഇന്റർപോളേറ്റഡ് ഫംഗ്ഷന്റെ മൂല്യങ്ങളുമായി പൊരുത്തപ്പെടുന്ന മൂല്യങ്ങളുടെ ഒരു നിര.

അരി. 10. മൂല്യങ്ങളുടെ പട്ടിക li(xj) (j=0,1,2,3), Ycalc(xj)

ചിലതിൽ മൂല്യങ്ങൾ കണക്കാക്കാൻ ഇന്റർമീഡിയറ്റ് പോയിന്റുകൾമതി

കോളം A യുടെ സെല്ലുകളിൽ, സെൽ A6 മുതൽ ആരംഭിക്കുന്നു, നിങ്ങൾ ഇന്റർപോളേറ്റഡ് ഫംഗ്ഷന്റെ മൂല്യങ്ങൾ നിർണ്ണയിക്കാൻ ആഗ്രഹിക്കുന്ന ആർഗ്യുമെന്റ് X ന്റെ മൂല്യങ്ങൾ നൽകുക. തിരഞ്ഞെടുക്കുക

പട്ടികയുടെ അവസാന (5-ാമത്തെ) വരിയിൽ, l0(xn) മുതൽ Ycalc(xn) വരെയുള്ള സെല്ലുകൾ തിരഞ്ഞെടുത്ത സെല്ലുകളിൽ എഴുതിയിരിക്കുന്ന ഫോർമുലകൾ അവസാനത്തേത് അടങ്ങുന്ന വരിയിലേക്ക് നീട്ടുക.

ആർഗ്യുമെന്റ് x ന്റെ നിർദ്ദിഷ്ട മൂല്യം.

ചിത്രത്തിൽ. ഫംഗ്‌ഷൻ മൂല്യം മൂന്ന് പോയിന്റുകളിൽ കണക്കാക്കുന്ന ഒരു പട്ടിക 11 കാണിക്കുന്നു: x=1, x=2, x=3. ഉറവിട ഡാറ്റ പട്ടികയുടെ വരി നമ്പറുകൾക്കൊപ്പം ഒരു അധിക കോളം പട്ടികയിൽ അവതരിപ്പിച്ചു.

അരി. 11. ലഗ്രാഞ്ച് ഫോർമുലകൾ ഉപയോഗിച്ച് ഇന്റർപോളേറ്റഡ് ഫംഗ്ഷനുകളുടെ മൂല്യങ്ങളുടെ കണക്കുകൂട്ടൽ

ഇന്റർപോളേഷന്റെ ഫലങ്ങൾ പ്രദർശിപ്പിക്കുന്നതിൽ കൂടുതൽ വ്യക്തതയ്ക്കായി, ആരോഹണ ക്രമത്തിൽ, നിരയിൽ ക്രമീകരിച്ച ആർഗ്യുമെന്റ് X മൂല്യങ്ങളുടെ ഒരു നിര ഉൾപ്പെടുന്ന ഒരു പട്ടിക ഞങ്ങൾ നിർമ്മിക്കും. പ്രാരംഭ മൂല്യങ്ങൾഫംഗ്ഷനുകൾY(X), കോളം

ഇന്റർപോളേഷൻ ഫോർമുല എങ്ങനെ ഉപയോഗിക്കാമെന്നും തെർമോഡൈനാമിക്സിലെ (ഹീറ്റ് എഞ്ചിനീയറിംഗ്) പ്രശ്നങ്ങൾ പരിഹരിക്കുന്നതിൽ ഏതാണ് ഉപയോഗിക്കേണ്ടതെന്നും എന്നോട് പറയൂ

ഇവാൻ ഷെസ്റ്റാകോവിച്ച്

ഏറ്റവും ലളിതവും എന്നാൽ പലപ്പോഴും കൃത്യമല്ലാത്തതുമായ ഇന്റർപോളേഷൻ രേഖീയമാണ്. നിങ്ങൾക്ക് ഇതിനകം അറിയപ്പെടുന്ന രണ്ട് പോയിന്റുകൾ (X1 Y1), (X2 Y2) ഉള്ളപ്പോൾ, X1 നും X2 നും ഇടയിൽ സ്ഥിതി ചെയ്യുന്ന ചില X ന്റെ ദിവസത്തെ Y മൂല്യങ്ങൾ നിങ്ങൾ കണ്ടെത്തേണ്ടതുണ്ട്. അപ്പോൾ ഫോർമുല ലളിതമാണ്.
Y=(U2-U1)*(X-X1)/(X2-X1)+U1
വഴിയിൽ, ഈ ഫോർമുല X1..X2 ഇടവേളയ്ക്ക് പുറത്തുള്ള X മൂല്യങ്ങൾക്കും പ്രവർത്തിക്കുന്നു, എന്നാൽ ഇത് ഇതിനകം എക്സ്ട്രാപോളേഷൻ എന്ന് വിളിക്കപ്പെടുന്നു, ഈ ഇടവേളയിൽ നിന്ന് ഗണ്യമായ അകലത്തിൽ ഇത് വളരെ വലിയ പിശക് നൽകുന്നു.
വേറെയും ധാരാളം ശകാരവാക്കുകൾ ഉണ്ട്. ഇന്റർപോളേഷൻ രീതികൾ - ഒരു പാഠപുസ്തകം വായിക്കാനോ ഇന്റർനെറ്റ് സ്കോർ ചെയ്യാനോ ഞാൻ നിങ്ങളെ ഉപദേശിക്കുന്നു.
ഗ്രാഫിക് ഇന്റർപോളേഷന്റെ രീതിയും സാധ്യമാണ് - അറിയപ്പെടുന്ന പോയിന്റുകളിലൂടെ ഒരു ഗ്രാഫ് സ്വമേധയാ വരയ്ക്കുകയും ആവശ്യമായ X-ന് വേണ്ടി ഗ്രാഫിൽ നിന്ന് Y കണ്ടെത്തുകയും ചെയ്യുക. ;)

നോവൽ

നിങ്ങൾക്ക് രണ്ട് അർത്ഥങ്ങളുണ്ട്. ഏകദേശം ആശ്രിതത്വം (ലീനിയർ, ക്വാഡ്രാറ്റിക്, ..)
ഈ ഫംഗ്‌ഷന്റെ ഗ്രാഫ് നിങ്ങളുടെ രണ്ട് പോയിന്റുകളിലൂടെ കടന്നുപോകുന്നു. അതിനിടയിൽ എവിടെയെങ്കിലും നിങ്ങൾക്ക് ഒരു മൂല്യം ആവശ്യമാണ്. ശരി, നിങ്ങൾ അത് പ്രകടിപ്പിക്കുക!
ഉദാഹരണത്തിന്. പട്ടികയിൽ, 22 ഡിഗ്രി താപനിലയിൽ, പൂരിത നീരാവി മർദ്ദം 120,000 Pa ആണ്, 26, 124,000 Pa ആണ്. അപ്പോൾ 23 ഡിഗ്രി 121000 Pa താപനിലയിൽ.

ഇന്റർപോളേഷൻ (കോർഡിനേറ്റുകൾ)

മാപ്പിൽ ഒരു കോർഡിനേറ്റ് ഗ്രിഡ് ഉണ്ട് (ചിത്രം).
അതിൽ അറിയപ്പെടുന്ന ചില റഫറൻസ് പോയിന്റുകൾ (n>3) ഉണ്ട്, ഓരോന്നിനും രണ്ടെണ്ണമുണ്ട് x,y മൂല്യങ്ങൾ- പിക്സലുകളിൽ കോർഡിനേറ്റുകളും മീറ്ററിൽ കോർഡിനേറ്റുകളും.
പിക്സലുകളിലെ കോർഡിനേറ്റുകൾ അറിഞ്ഞുകൊണ്ട് മീറ്ററിൽ ഇന്റർമീഡിയറ്റ് കോർഡിനേറ്റ് മൂല്യങ്ങൾ കണ്ടെത്തേണ്ടത് ആവശ്യമാണ്.
ലീനിയർ ഇന്റർപോളേഷൻ അനുയോജ്യമല്ല - ലൈനിന് പുറത്തുള്ള പിശക് വളരെ വലുതാണ്.
ഇതുപോലെ: (Xc എന്നത് മീറ്ററിൽ കോർഡിനേറ്റ് ആണ്, Xp എന്നത് കാളിനൊപ്പം പിക്സലിലുള്ള കോർഡിനേറ്റാണ്, Xc3 എന്നത് കാളയിൽ ആവശ്യമുള്ള മൂല്യമാണ്)
Xc3= (Xc1-Xc2)/(Xp1-Xp2)*(Xp3-Xp2)+Xc2
Yc3= (Yc1-Yc2)/(Yp1-Yp2)*(Yp3-Yp2)+Yc2

Xc, Yc എന്നിവ കണ്ടെത്തുന്നതിനുള്ള ഒരേ ഫോർമുല എങ്ങനെ കണ്ടെത്താം, രണ്ടല്ല (ഇവിടെയുള്ളത് പോലെ), N അറിയപ്പെടുന്ന റഫറൻസ് പോയിന്റുകൾ കണക്കിലെടുക്കുക?

ജോക്ക ഫേൺ ലോഡ്

രേഖാമൂലമുള്ള സൂത്രവാക്യങ്ങളാൽ വിലയിരുത്തുമ്പോൾ, പിക്സലുകളിലും മീറ്ററുകളിലും കോർഡിനേറ്റ് സിസ്റ്റങ്ങളുടെ അക്ഷങ്ങൾ യോജിക്കുന്നുണ്ടോ?
അതായത്, Xp -> Xc സ്വതന്ത്രമായും Yp -> Yc സ്വതന്ത്രമായും ഇന്റർപോളേറ്റ് ചെയ്യപ്പെടുന്നു. ഇല്ലെങ്കിൽ, നിങ്ങൾ Xp,Yp->Xc, Xp,Yp->Yc എന്നീ ദ്വിമാന ഇന്റർപോളേഷൻ ഉപയോഗിക്കേണ്ടതുണ്ട്, ഇത് ടാസ്ക്കിനെ കുറച്ച് സങ്കീർണ്ണമാക്കുന്നു.
എക്‌സ്‌പി, എക്‌സ്‌സി എന്നീ കോർഡിനേറ്റുകൾ ചില ആശ്രിതത്വത്താൽ ബന്ധപ്പെട്ടിരിക്കുന്നുവെന്ന് അനുമാനിക്കപ്പെടുന്നു.
ആശ്രിതത്വത്തിന്റെ സ്വഭാവം അറിയാമെങ്കിൽ (അല്ലെങ്കിൽ അനുമാനിക്കുകയാണെങ്കിൽ, ഉദാഹരണത്തിന്, Xc=a*Xp^2+b*Xp+c എന്ന് ഞങ്ങൾ അനുമാനിക്കുന്നു), അപ്പോൾ നമുക്ക് ഈ ആശ്രിതത്വത്തിന്റെ പരാമീറ്ററുകൾ ലഭിക്കും (നൽകിയിരിക്കുന്ന ആശ്രിതത്വത്തിന് a, b, c) ഉപയോഗിക്കുന്നു റിഗ്രഷൻ വിശകലനം(കുറഞ്ഞ ചതുര രീതി) . ഈ രീതിയിൽ, നിങ്ങൾ ഒരു നിശ്ചിത ആശ്രിതത്വം Xc (Xp) വ്യക്തമാക്കുകയാണെങ്കിൽ, റഫറൻസ് ഡാറ്റയെ ആശ്രയിക്കുന്നതിന്റെ പാരാമീറ്ററുകൾക്കായി നിങ്ങൾക്ക് ഒരു ഫോർമുല ലഭിക്കും. ഈ രീതി, പ്രത്യേകിച്ച്, കണ്ടെത്താനും അനുവദിക്കുന്നു രേഖീയ ആശ്രിതത്വം, ഏറ്റവും മികച്ച മാർഗ്ഗംതൃപ്തികരമായ ഈ സെറ്റ്ഡാറ്റ.
പോരായ്മ: ഈ രീതിയിൽ, Xp കൺട്രോൾ പോയിന്റുകളുടെ ഡാറ്റയിൽ നിന്ന് ലഭിച്ച Xc കോർഡിനേറ്റുകൾ വ്യക്തമാക്കിയതിൽ നിന്ന് വ്യത്യസ്തമായിരിക്കും. ഉദാഹരണത്തിന്, പരീക്ഷണ പോയിന്റുകളിലൂടെ വരച്ച ഏകദേശ നേർരേഖ ഈ പോയിന്റുകളിലൂടെ കൃത്യമായി കടന്നുപോകുന്നില്ല.
കൃത്യമായ കത്തിടപാടുകൾ ആവശ്യമാണെങ്കിൽ, ആശ്രിതത്വത്തിന്റെ സ്വഭാവം അജ്ഞാതമാണെങ്കിൽ, ഇന്റർപോളേഷൻ രീതികൾ ഉപയോഗിക്കേണ്ടതുണ്ട്. ഗണിതശാസ്ത്രപരമായി ഏറ്റവും ലളിതമായത് ലഗ്രാഞ്ച് ഇന്റർപോളേഷൻ പോളിനോമിയൽ ആണ്, അത് കൃത്യമായി റഫറൻസ് പോയിന്റുകളിലൂടെ കടന്നുപോകുന്നു. എന്നിരുന്നാലും, കാരണം ഉയർന്ന ബിരുദംഈ ബഹുപദം വലിയ സംഖ്യറഫറൻസ് പോയിന്റുകളും മോശം നിലവാരംഇന്റർപോളേഷൻ, അത് ഉപയോഗിക്കാതിരിക്കുന്നതാണ് നല്ലത്. താരതമ്യേന ലളിതമായ ഫോർമുലയാണ് നേട്ടം.
സ്പ്ലൈൻ ഇന്റർപോളേഷൻ ഉപയോഗിക്കുന്നതാണ് നല്ലത്. ഈ രീതിയുടെ സാരം, രണ്ട് അയൽ പോയിന്റുകൾക്കിടയിലുള്ള ഓരോ വിഭാഗത്തിലും, പഠനത്തിൻ കീഴിലുള്ള ആശ്രിതത്വം ഒരു ബഹുപദത്താൽ ഇന്റർപോളേറ്റ് ചെയ്യപ്പെടുന്നു, കൂടാതെ രണ്ട് ഇടവേളകളുടെ ചേരുന്ന പോയിന്റുകളിൽ സുഗമമായ അവസ്ഥകൾ എഴുതപ്പെടുന്നു എന്നതാണ്. ഈ രീതിയുടെ പ്രയോജനം ഇന്റർപോളേഷന്റെ ഗുണനിലവാരമാണ്. പോരായ്മകൾ - പിൻവലിക്കാൻ ഏതാണ്ട് അസാധ്യമാണ് പൊതു ഫോർമുല, ഓരോ വിഭാഗത്തിലെയും പോളിനോമിയലിന്റെ ഗുണകങ്ങൾ അൽഗോരിതമായി നിങ്ങൾ കണ്ടെത്തേണ്ടതുണ്ട്. ദ്വിമാന ഇന്റർപോളേഷനിലേക്ക് സാമാന്യവൽക്കരിക്കാനുള്ള ബുദ്ധിമുട്ടാണ് മറ്റൊരു പോരായ്മ.

ഇന്റർപോളേഷൻ എന്നത് ഒരു തരം ഏകദേശമാണ്, അതിൽ നിർമ്മിച്ച ഫംഗ്‌ഷന്റെ വക്രം ലഭ്യമായ ഡാറ്റ പോയിന്റുകളിലൂടെ കൃത്യമായി കടന്നുപോകുന്നു.

ഇന്റർപോളേഷനോട് അടുത്ത് ഒരു ടാസ്‌ക് ഉണ്ട്, അതിൽ ഒരു സങ്കീർണ്ണമായ ഫംഗ്‌ഷനെ മറ്റൊരു ലളിതമായ ഫംഗ്‌ഷന്റെ ഏകദേശ കണക്ക് ഉൾക്കൊള്ളുന്നു. ഒരു നിശ്ചിത ഫംഗ്‌ഷൻ ഉൽ‌പാദനപരമായ കണക്കുകൂട്ടലുകൾക്ക് വളരെ സങ്കീർണ്ണമാണെങ്കിൽ, നിങ്ങൾക്ക് അതിന്റെ മൂല്യം നിരവധി പോയിന്റുകളിൽ കണക്കാക്കാൻ ശ്രമിക്കാം, അവയിൽ നിന്ന് നിർമ്മിക്കുക, അതായത്, ഇന്റർപോളേറ്റ്, ഒരു ലളിതമായ പ്രവർത്തനം. തീർച്ചയായും, ലളിതമായ ഒരു ഫംഗ്‌ഷൻ ഉപയോഗിക്കുന്നത് യഥാർത്ഥ ഫംഗ്‌ഷൻ പോലെ കൃത്യമായ ഫലങ്ങൾ ഉണ്ടാക്കുന്നില്ല. എന്നാൽ ചില ക്ലാസുകളിലെ പ്രശ്‌നങ്ങളിൽ, കണക്കുകൂട്ടലുകളുടെ ലാളിത്യത്തിലും വേഗതയിലും നേടിയ നേട്ടം ഫലങ്ങളിൽ ഉണ്ടാകുന്ന പിശകിനെ മറികടക്കും.

ഓപ്പറേറ്റർ ഇന്റർപോളേഷൻ എന്നറിയപ്പെടുന്ന തികച്ചും വ്യത്യസ്തമായ ഒരു ഗണിത ഇന്റർപോളേഷനും എടുത്തുപറയേണ്ടതാണ്. ഓപ്പറേറ്റർ ഇന്റർപോളേഷനെക്കുറിച്ചുള്ള ക്ലാസിക് കൃതികളിൽ റൈസ്-തോറിൻ സിദ്ധാന്തവും മാർസിങ്കിവിച്ച് സിദ്ധാന്തവും ഉൾപ്പെടുന്നു, അവ മറ്റ് പല കൃതികൾക്കും അടിസ്ഥാനമാണ്.

നിർവചനങ്ങൾ

ഒരു നിശ്ചിത പ്രദേശത്ത് നിന്നുള്ള നോൺ-കോൺസിഡിങ്ങ് പോയിന്റുകളുടെ () ഒരു സിസ്റ്റം നമുക്ക് പരിഗണിക്കാം. ഫംഗ്‌ഷൻ മൂല്യങ്ങൾ ഈ പോയിന്റുകളിൽ മാത്രം അറിയട്ടെ:

ഒരു നിശ്ചിത ക്ലാസ് ഫംഗ്ഷനുകളിൽ നിന്ന് ഒരു ഫംഗ്ഷൻ കണ്ടെത്തുന്നതാണ് ഇന്റർപോളേഷൻ പ്രശ്നം

ഉദാഹരണം

1. താഴെ വിവരിച്ചിരിക്കുന്നതു പോലെ നമുക്ക് ഒരു ടേബിൾ ഫംഗ്ഷൻ ഉണ്ടായിരിക്കട്ടെ, അത് നിരവധി മൂല്യങ്ങൾക്ക് അനുബന്ധ മൂല്യങ്ങൾ നിർണ്ണയിക്കുന്നു:


0	0
1	0,8415
2	0,9093
3	0,1411
4	−0,7568
5	−0,9589
6	−0,2794

സൂചിപ്പിച്ചിരിക്കുന്നതല്ലാതെ മറ്റെവിടെയെങ്കിലും അത്തരമൊരു ഫംഗ്ഷന് എന്ത് മൂല്യമുണ്ടാകുമെന്ന് കണ്ടെത്താൻ ഇന്റർപോളേഷൻ ഞങ്ങളെ സഹായിക്കുന്നു (ഉദാഹരണത്തിന്, at x = 2,5).

ഇന്നുവരെ, നിരവധി വ്യത്യസ്ത ഇന്റർപോളേഷൻ രീതികളുണ്ട്. ഏറ്റവും അനുയോജ്യമായ അൽഗോരിതം തിരഞ്ഞെടുക്കുന്നത് ചോദ്യങ്ങൾക്കുള്ള ഉത്തരങ്ങളെ ആശ്രയിച്ചിരിക്കുന്നു: തിരഞ്ഞെടുത്ത രീതി എത്ര കൃത്യമാണ്, അത് ഉപയോഗിക്കുന്നതിനുള്ള ചെലവ് എന്താണ്, ഇന്റർപോളേഷൻ പ്രവർത്തനം എത്ര സുഗമമാണ്, അതിന് എത്ര ഡാറ്റ പോയിന്റുകൾ ആവശ്യമാണ്, മുതലായവ.

2. ഇന്റർമീഡിയറ്റ് മൂല്യം കണ്ടെത്തുക (ലീനിയർ ഇന്റർപോളേഷൻ വഴി).

6000	15.5
6378	?
8000	19.2

ഇന്റർപോളേഷൻ രീതികൾ

അടുത്തുള്ള അയൽക്കാരന്റെ ഇന്റർപോളേഷൻ

ഇന്റർപോളേഷന്റെ ഏറ്റവും ലളിതമായ രീതി അടുത്തുള്ള അയൽക്കാരനായ ഇന്റർപോളേഷൻ ആണ്.

ബഹുപദങ്ങൾ വഴിയുള്ള ഇന്റർപോളേഷൻ

IMN-1, IMN-2
ലഗ്രാഞ്ച് പോളിനോമിയൽ (ഇന്റർപോളേഷൻ പോളിനോമിയൽ)
എയ്റ്റ്കന്റെ പദ്ധതി പ്രകാരം

വിപരീത ഇന്റർപോളേഷൻ (എക്സ് കൊടുത്തിരിക്കുന്ന y കണക്കാക്കുന്നു)

ന്യൂട്ടന്റെ ഫോർമുല ഉപയോഗിച്ച് റിവേഴ്സ് ഇന്റർപോളേഷൻ

നിരവധി വേരിയബിളുകളുടെ ഒരു പ്രവർത്തനത്തിന്റെ ഇന്റർപോളേഷൻ

മറ്റ് ഇന്റർപോളേഷൻ രീതികൾ

ത്രികോണമിതി ഇന്റർപോളേഷൻ

ബന്ധപ്പെട്ട ആശയങ്ങൾ

എക്സ്ട്രാപോളേഷൻ - ഒരു നിശ്ചിത ഇടവേളയ്ക്ക് പുറത്തുള്ള പോയിന്റുകൾ കണ്ടെത്തുന്നതിനുള്ള രീതികൾ (കർവ് എക്സ്റ്റൻഷൻ)
ഏകദേശം - ഏകദേശ വളവുകൾ നിർമ്മിക്കുന്നതിനുള്ള രീതികൾ

ഇതും കാണുക

പരീക്ഷണാത്മക ഡാറ്റ സുഗമമാക്കൽ

വിക്കിമീഡിയ ഫൗണ്ടേഷൻ. 2010.

പര്യായപദങ്ങൾ:

മറ്റ് നിഘണ്ടുവുകളിൽ "ഇന്റർപോളേഷൻ" എന്താണെന്ന് കാണുക:

1) ഏതെങ്കിലും ഗണിതശാസ്ത്ര പദപ്രയോഗത്തിന്റെ നൽകിയിരിക്കുന്ന മൂല്യങ്ങളുടെ ഒരു ശ്രേണിയിൽ നിന്ന്, അതിന്റെ ഇന്റർമീഡിയറ്റ് മൂല്യങ്ങൾ നിർണ്ണയിക്കുന്നതിനുള്ള ഒരു മാർഗം; ഉദാഹരണത്തിന്, പീരങ്കി ചാനൽ അച്ചുതണ്ടിന്റെ 1°, 2°, 3°, 4° മുതലായവയുടെ എലവേഷൻ കോണിലുള്ള പീരങ്കിപ്പന്തിന്റെ ഫ്ലൈറ്റ് റേഞ്ച് അനുസരിച്ച്, ഇത് ഉപയോഗിച്ച് നിർണ്ണയിക്കാനാകും... ... റഷ്യൻ ഭാഷയുടെ വിദേശ പദങ്ങളുടെ നിഘണ്ടു

തിരുകൽ, ഇന്റർപോളേഷൻ, ഉൾപ്പെടുത്തൽ, റഷ്യൻ പര്യായപദങ്ങളുടെ നിഘണ്ടു തിരയുക. ഇന്റർപോളേഷൻ, ബോക്സ് കാണുക റഷ്യൻ ഭാഷയുടെ പര്യായപദങ്ങളുടെ നിഘണ്ടു. പ്രായോഗിക ഗൈഡ്. എം.: റഷ്യൻ ഭാഷ. Z. E. അലക്സാണ്ട്രോവ. 2... പര്യായപദ നിഘണ്ടു

ഇന്റർപോളേഷൻ- അറിയപ്പെടുന്ന രണ്ട് പോയിന്റുകൾക്കിടയിലുള്ള ഇന്റർമീഡിയറ്റ് മൂല്യങ്ങളുടെ കണക്കുകൂട്ടൽ. ഉദാഹരണത്തിന്: ലീനിയർ ലീനിയർ ഇന്റർപോളേഷൻ എക്‌സ്‌പോണൻഷ്യൽ എക്‌സ്‌പോണൻഷ്യൽ ഇന്റർപോളേഷൻ രണ്ട് വർണ്ണങ്ങൾക്കിടയിലുള്ള മേഖലയിൽ പിക്‌സലുകൾ വരുമ്പോൾ ഒരു കളർ ഇമേജ് ഔട്ട്‌പുട്ട് ചെയ്യുന്ന പ്രക്രിയ... ... സാങ്കേതിക വിവർത്തകന്റെ ഗൈഡ്

- (ഇന്റർപോളേഷൻ) അറിയപ്പെടുന്ന അളവുകളുടെ ഒരു ശ്രേണിയിലെ രണ്ട് പോയിന്റുകൾക്കിടയിൽ സ്ഥിതി ചെയ്യുന്ന ഒരു അജ്ഞാത അളവിന്റെ മൂല്യം കണക്കാക്കൽ. ഉദാഹരണത്തിന്, 10 വർഷത്തെ ഇടവേളകളിൽ നടത്തിയ ജനസംഖ്യാ സെൻസസിൽ നിന്ന് ലഭിച്ച രാജ്യത്തെ ജനസംഖ്യയുടെ സൂചകങ്ങൾ അറിയുന്നത്, നിങ്ങൾക്ക്... ... ബിസിനസ് നിബന്ധനകളുടെ നിഘണ്ടു

ലാറ്റിനിൽ നിന്ന്, യഥാർത്ഥത്തിൽ, "വ്യാജം". പകർപ്പെഴുത്തുകളോ വായനക്കാരോ ഉണ്ടാക്കിയ കൈയെഴുത്തുപ്രതികളിൽ തെറ്റായ ഭേദഗതികൾ അല്ലെങ്കിൽ പിന്നീട് ഉൾപ്പെടുത്തലുകൾക്ക് നൽകിയിരിക്കുന്ന പേരാണിത്. പുരാതന എഴുത്തുകാരുടെ കൈയെഴുത്തുപ്രതികളെ വിമർശിക്കാൻ ഈ പദം പലപ്പോഴും ഉപയോഗിക്കുന്നു. ഈ കയ്യെഴുത്തുപ്രതികളിൽ...... സാഹിത്യ വിജ്ഞാനകോശം

അറിയപ്പെടുന്ന നിരവധി മൂല്യങ്ങളെ അടിസ്ഥാനമാക്കി ഒരു നിശ്ചിത പാറ്റേണിന്റെ (ഫംഗ്ഷൻ) ഇന്റർമീഡിയറ്റ് മൂല്യങ്ങൾ കണ്ടെത്തുന്നു. ഇംഗ്ലീഷിൽ: ഇന്റർപോളേഷൻ ഇതും കാണുക: ഡാറ്റാ ട്രാൻസ്ഫോർമേഷൻസ് ഫിനാൻഷ്യൽ ഡിക്ഷണറി ഫിനാം... സാമ്പത്തിക നിഘണ്ടു

ഇന്റർപോളേഷൻ- ഒപ്പം, എഫ്. ഇന്റർപോളേഷൻ f. lat. ഇന്റർപോളേഷ്യോ മാറ്റം; മാറ്റം, വക്രീകരണം. 1. പിന്നീടുള്ള ഉത്ഭവത്തിന്റെ തിരുകൽ, അതിൽ l. ഒറിജിനലിൽ പെടാത്ത വാചകം. BAS 1. പ്രാചീന കയ്യെഴുത്തുപ്രതികളിൽ എഴുത്തുകാർ പരിചയപ്പെടുത്തിയ നിരവധി ഇന്റർപോളേഷനുകൾ ഉണ്ട്. ഉഷ്. 1934. 2… റഷ്യൻ ഭാഷയുടെ ഗാലിസിസത്തിന്റെ ചരിത്ര നിഘണ്ടു

ഇന്റർപോളേഷൻ- (ഇന്റർപോളേഷ്യോ), അനുഭവത്തിന്റെ നികത്തൽ. നഷ്‌ടമായ ഇന്റർമീഡിയറ്റ് മൂല്യങ്ങളുള്ള ഒരു അളവിന്റെ മൂല്യങ്ങളുടെ ഒരു ശ്രേണി. ഇന്റർപോളേഷൻ മൂന്ന് തരത്തിൽ ചെയ്യാം: ഗണിതശാസ്ത്രം, ഗ്രാഫിക്കൽ. യുക്തിസഹവും. അവ ഒരു പൊതു സിദ്ധാന്തത്തെ അടിസ്ഥാനമാക്കിയുള്ളതാണ്... ഗ്രേറ്റ് മെഡിക്കൽ എൻസൈക്ലോപീഡിയ

- (ലാറ്റിൻ ഇന്റർപോളേഷ്യോ മാറ്റം, മാറ്റം എന്നിവയിൽ നിന്ന്), അറിയപ്പെടുന്ന ചില മൂല്യങ്ങളെ അടിസ്ഥാനമാക്കി ഒരു അളവിന്റെ ഇന്റർമീഡിയറ്റ് മൂല്യങ്ങൾ കണ്ടെത്തുന്നു. ഉദാഹരണത്തിന്, x0, xn, x0 എന്നീ പോയിന്റുകൾക്കിടയിലുള്ള x പോയിന്റുകളിൽ y = f(x) ഫംഗ്‌ഷന്റെ മൂല്യങ്ങൾ കണ്ടെത്തുന്നത് ... ആധുനിക വിജ്ഞാനകോശം

- (ലാറ്റിൻ ഇന്റർപോളേഷ്യോ മാറ്റൽ മാറ്റത്തിൽ നിന്ന്), ഗണിതത്തിലും സ്ഥിതിവിവരക്കണക്കിലും, അറിയപ്പെടുന്ന ചില മൂല്യങ്ങളെ അടിസ്ഥാനമാക്കി ഒരു അളവിന്റെ ഇന്റർമീഡിയറ്റ് മൂല്യങ്ങൾ കണ്ടെത്തുന്നു. ഉദാഹരണത്തിന്, xo x1 പോയിന്റുകൾക്കിടയിലുള്ള x പോയിന്റുകളിൽ f(x) എന്ന ഫംഗ്‌ഷന്റെ മൂല്യങ്ങൾ കണ്ടെത്തുന്നു ... ബിഗ് എൻസൈക്ലോപീഡിക് നിഘണ്ടു

അറിയപ്പെടുന്ന മൂല്യങ്ങളുടെ ഒരു നിരയിൽ നിങ്ങൾ കണ്ടെത്തേണ്ട ഒരു സാഹചര്യമുണ്ട് ഇന്റർമീഡിയറ്റ് ഫലങ്ങൾ. ഗണിതശാസ്ത്രത്തിൽ ഇതിനെ ഇന്റർപോളേഷൻ എന്ന് വിളിക്കുന്നു. IN എക്സൽ നൽകിടാബുലാർ ഡാറ്റയ്ക്കും ഗ്രാഫുകൾ പ്ലോട്ടിംഗ് ചെയ്യുന്നതിനും ഈ രീതി ഉപയോഗിക്കാം. ഈ രീതികൾ ഓരോന്നും നോക്കാം.

ഇന്റർപോളേഷൻ ഉപയോഗിക്കാവുന്ന പ്രധാന വ്യവസ്ഥ, ആവശ്യമുള്ള മൂല്യം ഡാറ്റ അറേയ്‌ക്കുള്ളിൽ ആയിരിക്കണം, അതിന്റെ പരിധിക്ക് പുറത്തല്ല എന്നതാണ്. ഉദാഹരണത്തിന്, നമുക്ക് 15, 21, 29 എന്നീ ആർഗ്യുമെന്റുകൾ ഉണ്ടെങ്കിൽ, ആർഗ്യുമെന്റ് 25-ന്റെ ഫംഗ്ഷൻ കണ്ടെത്താൻ നമുക്ക് ഇന്റർപോളേഷൻ ഉപയോഗിക്കാം. എന്നാൽ ആർഗ്യുമെന്റ് 30-ന് അനുയോജ്യമായ മൂല്യം കണ്ടെത്താൻ ഇനി ഒരു മാർഗവുമില്ല. ഈ നടപടിക്രമവും എക്സ്ട്രാപോളേഷനും തമ്മിലുള്ള പ്രധാന വ്യത്യാസം ഇതാണ്.

രീതി 1: ടാബുലാർ ഡാറ്റയ്ക്കുള്ള ഇന്റർപോളേഷൻ

ഒന്നാമതായി, ഒരു പട്ടികയിൽ സ്ഥിതിചെയ്യുന്ന ഡാറ്റയ്ക്കുള്ള ഇന്റർപോളേഷന്റെ ആപ്ലിക്കേഷനുകൾ നോക്കാം. ഉദാഹരണത്തിന്, നമുക്ക് ആർഗ്യുമെന്റുകളുടെ ഒരു നിരയും അവയുടെ അനുബന്ധ ഫംഗ്ഷൻ മൂല്യങ്ങളും എടുക്കാം, അവയുടെ ബന്ധം വിവരിക്കാം. രേഖീയ സമവാക്യം. ഈ ഡാറ്റ ചുവടെയുള്ള പട്ടികയിൽ കാണിച്ചിരിക്കുന്നു. ആർഗ്യുമെന്റിനുള്ള അനുബന്ധ പ്രവർത്തനം നമ്മൾ കണ്ടെത്തേണ്ടതുണ്ട് 28 . ഇത് ചെയ്യാനുള്ള എളുപ്പവഴി ഓപ്പറേറ്റർ ഉപയോഗിക്കുക എന്നതാണ് പ്രവചനം.

രീതി 2: ഗ്രാഫ് അതിന്റെ ക്രമീകരണങ്ങൾ ഉപയോഗിച്ച് ഇന്റർപോളേറ്റ് ചെയ്യുക

ഫംഗ്ഷൻ ഗ്രാഫുകൾ നിർമ്മിക്കുമ്പോഴും ഇന്റർപോളേഷൻ നടപടിക്രമം ഉപയോഗിക്കാം. ഗ്രാഫ് അടിസ്ഥാനമാക്കിയുള്ള പട്ടിക ചുവടെയുള്ള ചിത്രത്തിലെന്നപോലെ ആർഗ്യുമെന്റുകളിലൊന്നിന്റെ അനുബന്ധ ഫംഗ്ഷൻ മൂല്യത്തെ സൂചിപ്പിക്കുന്നില്ലെങ്കിൽ അത് പ്രസക്തമാണ്.

നിങ്ങൾക്ക് കാണാനാകുന്നതുപോലെ, ഗ്രാഫ് ശരിയാക്കി, ഇന്റർപോളേഷൻ ഉപയോഗിച്ച് വിടവ് നീക്കം ചെയ്തു.

രീതി 3: ഒരു ഫംഗ്ഷൻ ഉപയോഗിച്ച് ഗ്രാഫ് ഇന്റർപോളേറ്റ് ചെയ്യുക

ഉപയോഗിച്ച് നിങ്ങൾക്ക് ഗ്രാഫ് ഇന്റർപോളേറ്റ് ചെയ്യാനും കഴിയും പ്രത്യേക പ്രവർത്തനംഎൻ.ഡി. അവൾ മടങ്ങുന്നു നിർവചിക്കാത്ത മൂല്യങ്ങൾനിർദ്ദിഷ്ട സെല്ലിലേക്ക്.

ഓടാതെ തന്നെ നിങ്ങൾക്ക് ഇത് ചെയ്യാൻ കഴിയും ഫംഗ്ഷൻ വിസാർഡ്, കൂടാതെ ഒരു ശൂന്യമായ സെല്ലിലേക്ക് മൂല്യം നൽകുന്നതിന് കീബോർഡ് ഉപയോഗിക്കുക "#N/A"ഉദ്ധരണികൾ ഇല്ലാതെ. എന്നാൽ ഇത് ഏത് ഉപയോക്താവിന് കൂടുതൽ സൗകര്യപ്രദമാണ് എന്നതിനെ ആശ്രയിച്ചിരിക്കുന്നു.

നിങ്ങൾക്ക് കാണാനാകുന്നതുപോലെ, Excel-ൽ നിങ്ങൾക്ക് ഫംഗ്ഷൻ ഉപയോഗിച്ച് ടാബ്ലർ ഡാറ്റയായി ഇന്റർപോളേറ്റ് ചെയ്യാൻ കഴിയും പ്രവചനം, ഒപ്പം ഗ്രാഫിക്സും. പിന്നീടുള്ള സാഹചര്യത്തിൽ, ഇത് ചാർട്ട് ക്രമീകരണങ്ങൾ ഉപയോഗിച്ചോ ഫംഗ്ഷൻ ഉപയോഗിച്ചോ ചെയ്യാം എൻ.ഡി, ഒരു പിശക് ഉണ്ടാക്കുന്നു "#N/A". ഏത് രീതിയാണ് ഉപയോഗിക്കേണ്ടതെന്ന് തിരഞ്ഞെടുക്കുന്നത് പ്രശ്ന പ്രസ്താവനയെയും ഉപയോക്താവിന്റെ വ്യക്തിഗത മുൻഗണനകളെയും ആശ്രയിച്ചിരിക്കുന്നു.

ബിൽ ജെലന്റെ പുസ്തകത്തിലെ ഒരു അധ്യായമാണിത്.

വെല്ലുവിളി: ചില എഞ്ചിനീയറിംഗ് ഡിസൈൻ പ്രശ്നങ്ങൾക്ക് പാരാമീറ്റർ മൂല്യങ്ങൾ കണക്കാക്കാൻ പട്ടികകൾ ആവശ്യമാണ്. പട്ടികകൾ വ്യതിരിക്തമായതിനാൽ, ഒരു ഇന്റർമീഡിയറ്റ് പാരാമീറ്റർ മൂല്യം ലഭിക്കുന്നതിന് ഡിസൈനർ ലീനിയർ ഇന്റർപോളേഷൻ ഉപയോഗിക്കുന്നു. പട്ടികയിൽ (ചിത്രം 1) നിലത്തിന് മുകളിലുള്ള ഉയരം (നിയന്ത്രണ പാരാമീറ്റർ), കാറ്റിന്റെ വേഗത (കണക്കാക്കിയ പാരാമീറ്റർ) എന്നിവ ഉൾപ്പെടുന്നു. ഉദാഹരണത്തിന്, 47 മീറ്റർ ഉയരത്തിന് അനുയോജ്യമായ കാറ്റിന്റെ വേഗത നിങ്ങൾക്ക് കണ്ടെത്തണമെങ്കിൽ, നിങ്ങൾ ഫോർമുല പ്രയോഗിക്കണം: 130 + (180 - 130) * 7 / (50 - 40) = 165 മീ / സെക്കന്റ്.

കുറിപ്പ് ഡൗൺലോഡ് ചെയ്യുക അല്ലെങ്കിൽ ഫോർമാറ്റിൽ, ഉദാഹരണങ്ങൾ ഫോർമാറ്റിൽ

രണ്ട് നിയന്ത്രണ പാരാമീറ്ററുകൾ ഉണ്ടെങ്കിൽ എന്തുചെയ്യും? ഒരു ഫോർമുല ഉപയോഗിച്ച് കണക്കുകൂട്ടലുകൾ നടത്താൻ കഴിയുമോ? പട്ടിക (ചിത്രം 2) ഘടനകളുടെ വിവിധ ഉയരങ്ങൾക്കും സ്പാനുകൾക്കുമുള്ള കാറ്റിന്റെ മർദ്ദ മൂല്യങ്ങൾ കാണിക്കുന്നു. 25 മീറ്റർ ഉയരത്തിലും 300 മീറ്റർ പരിധിയിലും കാറ്റിന്റെ മർദ്ദം കണക്കാക്കേണ്ടത് ആവശ്യമാണ്.

പരിഹാരം: ഒരു നിയന്ത്രണ പാരാമീറ്റർ ഉപയോഗിച്ച് കേസിനായി ഉപയോഗിക്കുന്ന രീതി വിപുലീകരിച്ച് ഞങ്ങൾ പ്രശ്നം പരിഹരിക്കുന്നു. ഈ ഘട്ടങ്ങൾ പാലിക്കുക:

ചിത്രത്തിൽ കാണിച്ചിരിക്കുന്ന പട്ടികയിൽ നിന്ന് ആരംഭിക്കുക. 2. J1, J2 എന്നിവയിൽ യഥാക്രമം ഉയരത്തിനും സ്‌പാനിനും സോഴ്‌സ് സെല്ലുകൾ ചേർക്കുക (ചിത്രം 3).

അരി. 3. സെല്ലുകളിലെ ഫോർമുലകൾ J3:J17 മെഗാഫോർമുലയുടെ പ്രവർത്തനത്തെ വിശദീകരിക്കുന്നു

ഫോർമുലകളുടെ എളുപ്പത്തിനായി, പേരുകൾ നിർവ്വചിക്കുക (ചിത്രം 4).

സെൽ J3-ൽ നിന്ന് സെൽ J17-ലേക്ക് തുടർച്ചയായി നീങ്ങിക്കൊണ്ട് ഫോർമുല വർക്ക് ചെയ്യുന്നത് കാണുക.

മെഗാഫോർമുല നിർമ്മിക്കാൻ റിവേഴ്സ് സീക്വൻഷ്യൽ സബ്സ്റ്റിറ്റ്യൂഷൻ ഉപയോഗിക്കുക. സെൽ J17-ൽ നിന്ന് J19-ലേക്ക് ഫോർമുല ടെക്സ്റ്റ് പകർത്തുക. ഫോർമുലയിലെ J15 എന്ന റഫറൻസ് സെല്ലിലെ മൂല്യം ഉപയോഗിച്ച് മാറ്റിസ്ഥാപിക്കുക: J7+(J8-J7)*J11/J13. ഇത്യാദി. ഫലം 984 പ്രതീകങ്ങൾ അടങ്ങുന്ന ഒരു ഫോർമുലയാണ്, ഈ രൂപത്തിൽ അത് മനസ്സിലാക്കാൻ കഴിയില്ല. അറ്റാച്ചുചെയ്തിരിക്കുന്ന Excel ഫയലിൽ നിങ്ങൾക്ക് ഇത് നോക്കാം. ഇത്തരത്തിലുള്ള മെഗാ ഫോർമുല ഉപയോഗിക്കുന്നതിന് ഉപയോഗപ്രദമാണോ എന്ന് എനിക്ക് ഉറപ്പില്ല.

സംഗ്രഹം: ഒരു പരാമീറ്ററിന്റെ ഇന്റർമീഡിയറ്റ് മൂല്യം ലഭിക്കാൻ ലീനിയർ ഇന്റർപോളേഷൻ ഉപയോഗിക്കുന്നു പട്ടിക മൂല്യങ്ങൾപരിധി അതിരുകൾക്കായി മാത്രം വ്യക്തമാക്കിയിരിക്കുന്നു; രണ്ട് നിയന്ത്രണ പാരാമീറ്ററുകൾ ഉപയോഗിച്ച് ഒരു കണക്കുകൂട്ടൽ രീതി നിർദ്ദേശിക്കപ്പെടുന്നു.