രീതി കൃത്രിമ അടിസ്ഥാനം(എം-ടാസ്ക്).

പ്രധാന പ്രശ്നത്തിന്റെ രൂപത്തിൽ എഴുതിയതും റഫറൻസ് പ്ലാനുകൾ ഉള്ളതുമായ നിരവധി ലീനിയർ പ്രോഗ്രാമിംഗ് പ്രശ്നങ്ങൾക്ക്, വെക്റ്ററുകളിൽ എപ്പോഴും m യൂണിറ്റ് വെക്റ്ററുകൾ ഉണ്ടാകില്ല.

ഇനിപ്പറയുന്ന പ്രശ്നം പരിഗണിക്കുക:

ഒരു ഫംഗ്‌ഷന്റെ പരമാവധി നമ്മൾ കണ്ടെത്തേണ്ടതുണ്ടെന്ന് കരുതുക

എഫ് = സി 1 x 1 + സി 2 x 2 + ……+ സി എൻ x എൻ (1)

വ്യവസ്ഥകൾ പ്രകാരം

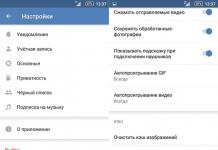
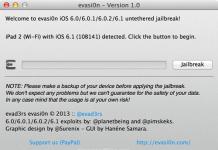
……………………………………… (2)

എവിടെ ബി ഐ  0 ( ഐ=l, m), എം<.>എൻകൂടാതെ P 1, P 2, ..., P n എന്നീ വെക്റ്ററുകളിൽ m യൂണിറ്റുകളൊന്നുമില്ല.

നിർവ്വചനം. ഒരു ഫംഗ്ഷന്റെ പരമാവധി മൂല്യം നിർണ്ണയിക്കുന്നതിനുള്ള ചുമതല

എഫ്= സി 1 x 1 + സി 2 x 2 + ……+ സി എൻ x എൻ -എംx എൻ +1 - ... - എംx എൻ + എം (3)

വ്യവസ്ഥകൾ പ്രകാരം

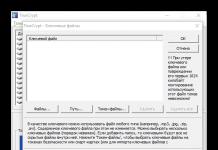
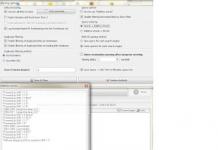
……………………………………… (4)

ഇവിടെ M എന്നത് മതിയായ പോസിറ്റീവ് സംഖ്യയാണ്, അതിന്റെ നിർദ്ദിഷ്ട മൂല്യം സാധാരണയായി വ്യക്തമാക്കിയിട്ടില്ല, പ്രശ്നം (1) - (2) മായി ബന്ധപ്പെട്ട് ഒരു വിപുലീകൃത പ്രശ്നം (M-ടാസ്ക്) എന്ന് വിളിക്കുന്നു.

വിപുലമായ ചുമതലയുണ്ട് റഫറൻസ് പ്ലാൻ

X=(0; 0; ...; 0; ബി 1 ; ബി 2 ; ...;ബി എം).

യൂണിറ്റ് വെക്റ്ററുകളുടെ സിസ്റ്റം നിർണ്ണയിച്ചിരിക്കുന്നു P n +1 ; ആർ n+2 , … ആർ p+t , m-ro വെക്റ്റർ സ്പേസിന്റെ അടിസ്ഥാനം ഉണ്ടാക്കുന്നു, അതിനെ വിളിക്കുന്നു കൃതിമമായ.വെക്റ്ററുകൾ സ്വയം, അതുപോലെ വേരിയബിളുകൾ x n + i ( ഐ=l, എം), വിളിക്കുന്നു കൃതിമമായ.വിപുലീകരിച്ച പ്രശ്നത്തിന് ഒരു റഫറൻസ് പ്ലാൻ ഉള്ളതിനാൽ, അതിന്റെ പരിഹാരം കണ്ടെത്താനാകും സിംപ്ലക്സ് രീതി.

സിദ്ധാന്തം ഒപ്റ്റിമൽ ആണെങ്കിൽ X*=( x* 1 , x* 2 , ...; x*എൻ , x* n +1 ; ...; x*n+m) വിപുലമായ ചുമതല (3) - (4) കൃത്രിമ വേരിയബിളുകളുടെ മൂല്യങ്ങൾ x* n + i =0 ( ഐ=1, എം), അത് X*=( x* 1 , x* 2 , ...; x*n) പ്രശ്നത്തിനുള്ള ഒപ്റ്റിമൽ പ്ലാൻ ആണ് (1) - (2).

അതിനാൽ, വിപുലീകൃത പ്രശ്നത്തിന് കണ്ടെത്തിയ ഒപ്റ്റിമൽ പ്ലാനിൽ, കൃത്രിമ വേരിയബിളുകളുടെ മൂല്യങ്ങൾ പൂജ്യത്തിന് തുല്യമാണെങ്കിൽ, യഥാർത്ഥ പ്രശ്നത്തിനുള്ള ഒപ്റ്റിമൽ പ്ലാൻ ലഭിക്കും.

ഇൻഡക്സ് ലൈൻ മൂല്യങ്ങൾ ∆ 0 , ∆ 1 , ..., ∆ n രണ്ട് ഭാഗങ്ങൾ ഉൾക്കൊള്ളുന്നു, അവയിലൊന്നിനെ ആശ്രയിച്ചിരിക്കുന്നു എം,എന്നാൽ മറ്റേയാൾ ചെയ്യുന്നില്ല. ഒരു സാധാരണ സിംപ്ലക്സ് ടേബിളിനേക്കാൾ ഒരു വരി കൂടി അടങ്ങുന്ന സിംപ്ലക്സ് ടേബിൾ പൂരിപ്പിക്കുക. ഈ സാഹചര്യത്തിൽ, (m+2)th വരിയിൽ ഗുണകങ്ങൾ അടങ്ങിയിരിക്കുന്നു എം,കൂടാതെ (m+1)-ൽ - അടങ്ങാത്ത നിബന്ധനകൾ എം.ഒരു റഫറൻസ് പ്ലാനിൽ നിന്ന് മറ്റൊന്നിലേക്ക് നീങ്ങുമ്പോൾ, (m+2) വരിയുടെ കേവല മൂല്യത്തിലെ ഏറ്റവും വലിയ നെഗറ്റീവ് സംഖ്യയുമായി ബന്ധപ്പെട്ട ഒരു വെക്റ്റർ അടിസ്ഥാനത്തിലേക്ക് അവതരിപ്പിക്കുന്നു. അടിസ്ഥാനത്തിൽ നിന്ന് ഒഴിവാക്കിയ ഒരു കൃത്രിമ വെക്റ്റർ ഇനിപ്പറയുന്ന സിംപ്ലക്സ് പട്ടികയിൽ രേഖപ്പെടുത്തിയിട്ടില്ല. ഒരു റഫറൻസ് പ്ലാനിൽ നിന്ന് മറ്റൊന്നിലേക്ക് മാറുമ്പോൾ സിംപ്ലക്സ് ടേബിളുകളുടെ വീണ്ടും കണക്കുകൂട്ടൽ അനുസരിച്ച് നടപ്പിലാക്കുന്നു പൊതു നിയമങ്ങൾസിംപ്ലക്സ് രീതി.

(m+2)-ലൈൻ വഴിയുള്ള ആവർത്തന പ്രക്രിയ ഇത് വരെ തുടരുന്നു:

ഒന്നുകിൽ എല്ലാ കൃത്രിമ വെക്റ്ററുകളും അടിസ്ഥാനത്തിൽ നിന്ന് ഒഴിവാക്കില്ല;

അല്ലെങ്കിൽ എല്ലാ കൃത്രിമ വെക്റ്ററുകളും ഒഴിവാക്കിയിട്ടില്ല, എന്നാൽ (m+2)മത്തെ വരിയിൽ ∆ 1, ..., ∆ n സൂചികകളിൽ കൂടുതൽ നെഗറ്റീവ് ഘടകങ്ങളൊന്നും അടങ്ങിയിട്ടില്ല.

ആദ്യ സന്ദർഭത്തിൽ, അടിസ്ഥാനം യഥാർത്ഥ പ്രശ്നത്തിന്റെ ചില റഫറൻസ് പ്ലാനുമായി പൊരുത്തപ്പെടുന്നു കൂടാതെ അതിന്റെ ഒപ്റ്റിമൽ പ്ലാനിന്റെ നിർണ്ണയം (m+1)th വരിയിൽ തുടരുന്നു.

രണ്ടാമത്തെ സാഹചര്യത്തിൽ, ∆ 0 ന്റെ മൂല്യം നെഗറ്റീവ് ആണെങ്കിൽ, യഥാർത്ഥ പ്രശ്നത്തിന് പരിഹാരമില്ല; ∆ 0 =0 ആണെങ്കിൽ, യഥാർത്ഥ പ്രശ്നത്തിന്റെ കണ്ടെത്തിയ റഫറൻസ് പ്ലാൻ ഡീജനറേറ്റ് ആണ്, കൂടാതെ അടിസ്ഥാനത്തിൽ കൃത്രിമ അടിസ്ഥാന വെക്റ്ററുകളിൽ ഒന്നെങ്കിലും അടങ്ങിയിരിക്കുന്നു.

പ്രശ്നത്തിന് പരിഹാരം കണ്ടെത്തുന്നതിനുള്ള ഘട്ടങ്ങൾ (1) - (2)

കൃത്രിമ അടിസ്ഥാന രീതി:

ഒരു വിപുലീകൃത പ്രശ്നം രചിക്കുക (3) - (4).

വിപുലീകരിച്ച പ്രശ്നത്തിന്റെ റഫറൻസ് പ്ലാൻ കണ്ടെത്തുക.

ഉപയോഗിച്ച് സാധാരണ കണക്കുകൂട്ടലുകൾസിംപ്ലക്സ് രീതി അടിസ്ഥാനത്തിൽ നിന്ന് കൃത്രിമ വേരിയബിളുകൾ ഒഴിവാക്കുന്നു. തൽഫലമായി, ഒന്നുകിൽ യഥാർത്ഥ പ്രശ്നത്തിന്റെ റഫറൻസ് പ്ലാൻ (1) - (2) കണ്ടെത്തി, അല്ലെങ്കിൽ അതിന്റെ പരിഹരിക്കാനാകാത്തത് സ്ഥാപിക്കപ്പെടുന്നു.

പ്രശ്നത്തിന്റെ കണ്ടെത്തിയ റഫറൻസ് പ്ലാൻ ഉപയോഗിച്ച് (1) - (2), അവർ ഒന്നുകിൽ സിംപ്ലക്സ് രീതി ഉപയോഗിച്ച് യഥാർത്ഥ പ്രശ്നത്തിന്റെ ഒപ്റ്റിമൽ പ്ലാൻ കണ്ടെത്തുന്നു, അല്ലെങ്കിൽ അതിന്റെ പരിഹരിക്കാനാകാത്തത് സ്ഥാപിക്കുക.

ഉദാഹരണം.

ഒരു ഫംഗ്‌ഷന്റെ ഏറ്റവും കുറഞ്ഞ തുക കണ്ടെത്തുക എഫ്= - 2x 1 + 3x 2 - 6x 3 - x 4

പി നിയന്ത്രണങ്ങളോടെ:

2x 1 +x 2 -2x 3 +x 4 =24

x 1 +2x 2 +4x 3 ≤22

x 1 -x 2 +2x 3 ≥10

x ഐ ≥0, ഐ=1,4

പരിഹാരം.

നമുക്ക് അത് എഴുതാം ഈ ചുമതലപ്രധാന പ്രശ്നത്തിന്റെ രൂപത്തിൽ: പ്രവർത്തനത്തിന്റെ പരമാവധി കണ്ടെത്തുക എഫ്= 2x 1 - 3x 2 + 6x 3 + x 4

നിയന്ത്രണങ്ങളോടെ:

2x 1 +x 2 -2x 3 +x 4 =24

x 1 +2x 2 +4x 3 +x 5 =22

x 1 -x 2 +2x 3 - x 6= 10

x ഐ ≥0, ഐ=1, 6

അവസാന പ്രശ്നത്തിന്റെ സമവാക്യങ്ങളുടെ സിസ്റ്റത്തിൽ, അജ്ഞാതർക്കുള്ള ഗുണകങ്ങളുടെ വെക്റ്ററുകൾ പരിഗണിക്കുക:

വെക്റ്ററുകളിൽ പി 1, ആർ 2 , ... പി 6 രണ്ടെണ്ണം മാത്രം (പി 4, പി 5). അതിനാൽ ഇൻ ഇടത് വശംപ്രശ്ന നിയന്ത്രണ സംവിധാനത്തിന്റെ മൂന്നാമത്തെ സമവാക്യത്തിൽ, ഞങ്ങൾ ഒരു അധിക നോൺ-നെഗറ്റീവ് വേരിയബിൾ x ചേർക്കുന്നു 7 ഫംഗ്‌ഷൻ പരമാവധിയാക്കുന്നതിനുള്ള വിപുലമായ പ്രശ്‌നം പരിഗണിക്കുക

എഫ്= 2x 1 - 3x 2 + 6x 3 + x 4 - എം 7

നിയന്ത്രണങ്ങളോടെ:

2x 1 +x 2 -2x 3 +x 4 =24

x 1 +2x 2 +4x 3 +x 5 =22

x 1 -x 2 +2x 3 - x 6 +x 7= 10

വിപുലീകൃത പ്രശ്നത്തിന് ഒരു റഫറൻസ് പ്ലാൻ X = (0; 0; 0; 24; 22; 0; 10) ഉണ്ട്, മൂന്ന് യൂണിറ്റ് വെക്റ്ററുകളുടെ ഒരു സിസ്റ്റം നിർവ്വചിച്ചിരിക്കുന്നു: P 4 , P 5 , P 7 .

ഇരട്ട (അനുബന്ധ) പ്രശ്നത്തിന്റെ ആശയം ലീനിയർ പ്രോഗ്രാമിംഗ്.

നിർമ്മാണ നിയമങ്ങൾ ഇരട്ട പ്രശ്നം.

ഓരോ ലീനിയർ പ്രോഗ്രാമിംഗ് പ്രശ്‌നത്തിലും (LPP), യഥാർത്ഥ പ്രശ്‌നവുമായി ബന്ധപ്പെട്ട് ഇരട്ട പ്രശ്‌നം (അല്ലെങ്കിൽ അനുബന്ധം) എന്ന് വിളിക്കുന്നു, അതിനെ നേരിട്ടുള്ള ഒന്ന് എന്ന് വിളിക്കുന്നു.

സ്റ്റാൻഡേർഡ് രൂപത്തിൽ എഴുതിയ നേരിട്ടുള്ള പ്രശ്നവുമായി ബന്ധപ്പെട്ട് ഇരട്ട പ്രശ്നം നിർമ്മിച്ചിരിക്കുന്നു:

F=c 1 x 1 +c 2 x 2 +…+c n x n  പരമാവധി (3.6)

a 11 x 1 +a 12 x 2 +…+a 1n x n ≤ b 1,

a 21 x 1 +a 22 x 2 +…+a 2n x n ≤ b 2,

………………………………

a k1 x 1 +a k2 x 2 +…+a kn x n ≤ =b k , (3.7)

a k+1.1 x 1 +a k+1.2 x 2 +…+a k+1,n x n =b k+1 ,

………………………………

a m1 x 1 +a m2 x 2 +…+a mn x n =b m,

x j ≥ 0, , എൽ≤ n (3.8)

ഒരു ഫംഗ്ഷന്റെ ഏറ്റവും കുറഞ്ഞ മൂല്യം കണ്ടെത്തുന്നതിനുള്ള പ്രശ്നം

L = b 1 y 1 + b 2 y 2 + ... + b m y m (3.9)

വ്യവസ്ഥകൾ പ്രകാരം

a 11 y 1 + a 12 y 2 +…+ a m1 y m ≥ c 1

a 21 y 1 + a 22 y 2 +…+ a m2 y m ≥ c 2

………………………………

a 1 എൽ y 1 + a 2 എൽ y 2 +…+ ഒരു മ എൽ y m≥ c എൽ (3.10)

എ എൽ+1.1 y 1 + എ എൽ+1.2 y 2 +…+ എ എൽ+1,m y m = c l+1

………………………………

a m1 y 1 + a m2 y 2 +…+ a mn y m = c m

y i ≥ 0, , k ≤ m (3.11)

ഡ്യുവൽ ടു പ്രശ്നം (3.6) - (3.8) എന്ന് വിളിക്കുന്നു.

ഇരട്ട പ്രശ്നം നിർമ്മിക്കുന്നതിനുള്ള നിയമങ്ങൾ പട്ടികയിൽ നൽകിയിരിക്കുന്നു:

ZLP യുടെ ഘടനാപരമായ സവിശേഷതകൾ	ലീനിയർ പ്രോഗ്രാമിംഗ് പ്രശ്നം
		ഇരട്ട
1. ഒബ്ജക്റ്റീവ് ഫംഗ്ഷൻ	പരമാവധിയാക്കൽ (പരമാവധി)	ചെറുതാക്കൽ (മിനിറ്റ്)
2. വേരിയബിളുകളുടെ എണ്ണം	n വേരിയബിളുകൾ	നേരിട്ടുള്ള പ്രശ്നത്തിന്റെ (3.7) നിയന്ത്രണങ്ങളുടെ എണ്ണത്തിന് തുല്യമാണ്, y i , i.e. എം
3. നിയന്ത്രണങ്ങളുടെ എണ്ണം	മീറ്റർ നിയന്ത്രണങ്ങൾ	നേരിട്ടുള്ള പ്രശ്നത്തിന്റെ വേരിയബിളുകളുടെ എണ്ണത്തിന് തുല്യമാണ് x j , അതായത് n
4. നിയന്ത്രണ സംവിധാനത്തിലെ ഗുണകങ്ങളുടെ മാട്രിക്സ്
5. ഒബ്ജക്റ്റീവ് ഫംഗ്ഷനിലെ വേരിയബിളുകളുടെ ഗുണകങ്ങൾ	c 1 ,c 2, ...,c n	b 1 ,b 2, ...,b m
6. വലത് ഭാഗംനിയന്ത്രണങ്ങളുടെ സംവിധാനങ്ങൾ	b 1 ,b 2, ...,b m	c 1 ,c 2, ...,c n
7. നിയന്ത്രണങ്ങളുടെ സംവിധാനത്തിലെ അടയാളങ്ങൾ	a) x j ≥ 0 - നോൺ-നെഗറ്റിവിറ്റി അവസ്ഥ	jth പരിമിതിക്ക് "≥" എന്ന ചിഹ്നമുണ്ട്
	b) x j എന്ന വേരിയബിളിൽ നോൺ-നെഗറ്റിവിറ്റി വ്യവസ്ഥ ചുമത്തിയിട്ടില്ല	jth പരിമിതിക്ക് “=” ചിഹ്നമുണ്ട്
	c) i-th പരിമിതിക്ക് "≤" എന്ന ചിഹ്നമുണ്ട്	വേരിയബിൾ y i ≥0
	d) i-th നിയന്ത്രണത്തിന് “=” ചിഹ്നമുണ്ട്	y i എന്ന വേരിയബിളിൽ നോൺ-നെഗറ്റിവിറ്റി വ്യവസ്ഥ ചുമത്തിയിട്ടില്ല

കുറിപ്പ്

നേരിട്ടുള്ള പരമാവധി പ്രശ്‌നവും ഇരട്ട മിനിമം പ്രശ്‌നവും പരസ്പരമുള്ള ഇരട്ട പ്രശ്‌നങ്ങളാണ്. അതിനാൽ, നമുക്ക് പ്രശ്നം (3.9) - (3.11) നേരിട്ടുള്ള ZLP, പ്രശ്നം (3.6) - (3.8) അതിന്റെ ഇരട്ട പ്രശ്നം എന്നിവ പരിഗണിക്കാം. ഈ സാഹചര്യത്തിൽ, ഒരു ഡ്യുവൽ PLP നിർമ്മിക്കുന്നതിനുള്ള നിയമങ്ങൾ സംരക്ഷിക്കപ്പെടുന്നു, കൂടെ മാത്രം ആ മാറ്റത്താൽ, ഏറ്റവും കുറഞ്ഞ പ്രശ്നം പ്രാഥമികമായി കണക്കാക്കുന്നു.

യഥാർത്ഥ പ്രശ്നം പരമാവധി (മിനിറ്റ്) ലും നിയന്ത്രണങ്ങളുടെ സംവിധാനത്തിലും പരിഹരിച്ചാൽ ഐ-ഇ ( ജെ-f) നിയന്ത്രണത്തിന് “≤” (“≥”) ചിഹ്നമുണ്ട്, തുടർന്ന് ഇരട്ട പ്രശ്നം നിർമ്മിക്കുന്നതിന് ഇത് ആവശ്യമാണ്:

a) അല്ലെങ്കിൽ രണ്ട് ഭാഗങ്ങളും ഗുണിക്കുക ഐ th ( ജെ-th) അസമത്വം (-1) വഴി അടയാളം മാറ്റുക "≤" ("≥")

b) അല്ലെങ്കിൽ കൊണ്ടുവരിക ഐ-ഇ ( ജെ-e) ഒരു അധിക വേരിയബിൾ x അവതരിപ്പിക്കുന്നതിലൂടെ സമത്വത്തിലേക്കുള്ള നിയന്ത്രണം n+ ഐ ≥0

നമുക്ക് ഫോമിൽ ZLP പരിഹരിക്കാം

ഈ സാഹചര്യത്തിൽ പൊതു പദ്ധതിസിംപ്ലക്സ് രീതിചില മാറ്റങ്ങൾക്ക് വിധേയമാകുന്നു. അതായത്:

1) ചില പിന്തുണാ പരിഹാരത്തിന്റെ അടിസ്ഥാനവും അതിന്റെ അനുബന്ധവും അനുവദിക്കുക സിംപ്ലക്സ് ടേബിൾ. IN മുകളിലെ വരിഈ പട്ടികയിൽ (കോളം തലക്കെട്ടുകൾ) സ്വതന്ത്ര വേരിയബിളുകൾ അടങ്ങിയിരിക്കുന്നു, ഇടതുവശത്തെ കോളത്തിൽ അടിസ്ഥാന വേരിയബിളുകൾ അടങ്ങിയിരിക്കുന്നു; വലത്തേയറ്റത്തെ കോളം സ്വതന്ത്ര അംഗങ്ങളുടെ കോളമാണ്, ഏറ്റവും കൂടുതൽ താഴെ വരിഒരു ചരടാണ് വസ്തുനിഷ്ഠമായ പ്രവർത്തനംആപേക്ഷിക എസ്റ്റിമേറ്റുകളുടെ വെക്റ്റർ എന്ന് വിളിക്കുന്നു. ബാക്കിയുള്ള പട്ടിക ഉള്ളടക്കങ്ങൾ ഫ്രീ വേരിയബിളുകളുടെ അനുബന്ധ നിരകളുമായി ബന്ധപ്പെട്ട കൺസ്ട്രെയിന്റ് മാട്രിക്സിന്റെ നിരകളാണ്. ആപേക്ഷിക എസ്റ്റിമേറ്റുകളുടെ വെക്റ്ററിന്റെ കോർഡിനേറ്റുകൾ റൂൾ അനുസരിച്ച് കാണപ്പെടുന്നു: ഒബ്ജക്റ്റീവ് ഫംഗ്ഷനിലെ അടിസ്ഥാന വേരിയബിളുകളുടെ ഗുണകങ്ങളുടെ വെക്റ്റർ സ്കെയിലർ ആയി ഗുണിക്കുന്നു ഐസിംപ്ലെക്‌സ് ടേബിളിന്റെ th കോളം, കണ്ടെത്തിയ സംഖ്യയിൽ നിന്ന് അനുബന്ധ ഫ്രീ വേരിയബിളിനുള്ള ഒബ്ജക്റ്റീവ് ഫംഗ്‌ഷന്റെ ഗുണകം കുറയ്ക്കുക.

2) എല്ലാ ആപേക്ഷിക എസ്റ്റിമേറ്റുകളും (ഈ പട്ടികയുടെ താഴത്തെ വരി) നെഗറ്റീവ് അല്ലെങ്കിൽ, ഒരു ഒപ്റ്റിമൽ റഫറൻസ് സൊല്യൂഷൻ നിർമ്മിച്ചു.

3) ഒരു നെഗറ്റീവ് എസ്റ്റിമേറ്റ് ഉണ്ടെങ്കിൽ, അനുബന്ധ കോളം (പരിഹരിക്കുന്നത്) പോസിറ്റീവ് അല്ലാത്ത ഘടകങ്ങൾ ഉൾക്കൊള്ളുന്നുവെങ്കിൽ, വസ്തുനിഷ്ഠമായ പ്രവർത്തനം പരിഹരിക്കാനാവില്ല Z(എക്സ്), അതായത്, പരമാവധി Z(എക്സ്) ®+¥.

4) അല്ലാത്തപക്ഷം, മുൻനിര ഘടകം തിരഞ്ഞെടുത്ത് (മുൻനിര നിര വ്യക്തമാക്കുന്നു) അതിനൊപ്പം ജോർദാൻ എലിമിനേഷൻ ഘട്ടം നടത്തുക, ഒരു പുതിയ സിംപ്ലക്സ് പട്ടികയിലേക്ക് നീങ്ങുക, അത് പോയിന്റ് 2 ൽ വിശകലനം ചെയ്യുന്നു).

കൃത്രിമ അടിസ്ഥാന രീതി

യൂണിറ്റ് വെക്റ്ററുകളുടെ അടിസ്ഥാനത്തിലുള്ള ഒരു പ്രാരംഭ റഫറൻസ് സൊല്യൂഷൻ പ്രശ്നത്തിന് ഇല്ലെങ്കിൽ, എൽപി പ്രശ്നങ്ങൾ പരിഹരിക്കാൻ കൃത്രിമ അടിസ്ഥാന രീതി ഉപയോഗിക്കുന്നു.

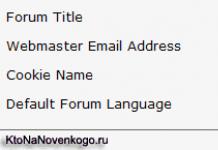
എൽപി പ്രശ്നം നൽകട്ടെ കാനോനിക്കൽ രൂപം, അതായത്, ഇതിന് ഫോം (2.1.1) ഉണ്ട്, അതിൽ യൂണിറ്റ് അടിസ്ഥാനമില്ല. ഈ പ്രശ്നത്തിന് ഞങ്ങൾ ഒരു സഹായ പ്രശ്നം (AP) നിർമ്മിക്കുന്നു:

ഇവിടെ w 1 , w 2 ,…, w m- കൃത്രിമ വേരിയബിളുകൾ. വെക്റ്റർ രൂപത്തിൽ നിയന്ത്രണങ്ങൾ എഴുതാം: എ 1 x 1 +എ 2 x 2 +…+എ എൻ എക്സ് എൻ+എ എൻ +1 w 1 +…+A n + m w m =ബി, എവിടെ , , ..., , , , ..., , . അങ്ങനെ, വെക്‌ടറുകൾ, , ..., ഒരു യൂണിറ്റ് അടിസ്ഥാനമായി മാറുന്നു ആർ എം, കൂടാതെ ഈ വെക്റ്ററുകളുമായി ബന്ധപ്പെട്ട എല്ലാ കൃത്രിമ വേരിയബിളുകളും അടിസ്ഥാനമായിരിക്കും. അടുത്തതായി, ഒരു സാധാരണ സിംപ്ലക്സ് ടേബിൾ നിർമ്മിക്കുന്നു. വസ്തുനിഷ്ഠമായ പ്രവർത്തനത്തിന്റെ പരിധിയില്ലാത്തതിനാൽ പ്രശ്നത്തിന് പരിഹാരമില്ലെങ്കിൽ, അതേ കാരണത്താൽ യഥാർത്ഥ പ്രശ്നത്തിനും പരിഹാരമില്ല. സിംപ്ലക്സ് രീതിയിൽ നിന്ന് പരിചിതമായ ആവശ്യമായ പരിവർത്തനങ്ങളുടെ ഫലമായി, നമുക്ക് VZ-നുള്ള ഒപ്റ്റിമൽ സിംപ്ലക്സ് ടേബിൾ ലഭിക്കുമെന്ന് നമുക്ക് അനുമാനിക്കാം. അത് വ്യക്തമാണ് പരമാവധി മൂല്യംഒബ്ജക്റ്റീവ് ഫംഗ്ഷൻ VZ 0 ന് തുല്യമാണ്, അതായത് പരമാവധി എഫ്=0. പരമാവധി ആണെങ്കിൽ എഫ്<0, то исходная задача ЛП не имеет решения в силу несовместности системы ограничений. Предположим, что max എഫ്=0. അപ്പോൾ ഇനിപ്പറയുന്ന സാഹചര്യങ്ങൾ സാധ്യമാണ്:

1) എല്ലാ കൃത്രിമ വേരിയബിളുകളും സ്വതന്ത്രമാവുകയും പട്ടികയിൽ നിന്ന് ഒഴിവാക്കപ്പെടുകയും ചെയ്തു. ഈ സാഹചര്യത്തിൽ, കൃത്രിമ വേരിയബിളുകൾക്കും അവസാന നിരയ്ക്കും അനുയോജ്യമായ നിരകൾ ഞങ്ങൾ മറികടക്കുന്നു. പകരം, ഞങ്ങൾ എസ്റ്റിമേറ്റുകളുടെ ഒരു പുതിയ വരി നൽകുന്നു, എന്നാൽ യഥാർത്ഥ ഒബ്ജക്റ്റീവ് ഫംഗ്ഷൻ ഉപയോഗിക്കുന്നു Z(എക്സ്). അങ്ങനെ, യഥാർത്ഥ എൽപി പ്രശ്നത്തിനായുള്ള പ്രാരംഭ സിംപ്ലക്സ് ടേബിൾ ഞങ്ങൾക്ക് ലഭിച്ചു, അതിന് ഞങ്ങൾ സിംപ്ലക്സ് രീതി പ്രയോഗിക്കുന്നു;

2) പ്രശ്നത്തിന്റെ ഒപ്റ്റിമൽ പരിഹാരത്തിൽ, കുറഞ്ഞത് ഒരു കൃത്രിമ വേരിയബിളെങ്കിലും അടിസ്ഥാനമായി തുടരുന്നു. അപ്പോൾ:

a) ഒന്നുകിൽ ബാക്കിയുള്ള അടിസ്ഥാന കൃത്രിമ വേരിയബിളുകളുമായി ബന്ധപ്പെട്ട വരികളിലെ എല്ലാ സംഖ്യകളും 0 ന് തുല്യമാണ്;

b) അല്ലെങ്കിൽ 0-ൽ നിന്ന് കുറഞ്ഞത് ഒരെണ്ണമെങ്കിലും ഉണ്ട്.

ആദ്യ സന്ദർഭത്തിൽ, ഞങ്ങൾ പോയിന്റ് 1-ൽ ഉള്ളതുപോലെ തന്നെ ചെയ്യുന്നു). രണ്ടാമത്തേതിൽ, ഞങ്ങൾ ഏതെങ്കിലും നോൺ-സീറോ ഘടകത്തെ മുൻനിര ഘടകമായി തിരഞ്ഞെടുത്ത് ജോർദാൻ എലിമിനേഷൻ ഘട്ടം നടത്തുന്നു. ഒരു നിശ്ചിത എണ്ണം ഘട്ടങ്ങൾക്ക് ശേഷം ഞങ്ങൾ പോയിന്റ് 1) അല്ലെങ്കിൽ പോയിന്റ് 2)a) എത്തും.

വെക്റ്ററുകൾക്കിടയിൽ ആണെങ്കിൽ ശ്രദ്ധിക്കുക എ ജെ , ജെ=1,2,…,എൻ, അടിസ്ഥാനത്തിലേക്ക് പ്രവേശിക്കാൻ കഴിയുന്ന വെക്റ്ററുകൾ ഉണ്ടായിരുന്നു, പിന്നെ കൃത്രിമ വേരിയബിളുകൾ അടിസ്ഥാന വേരിയബിൾ ഇല്ലാത്ത നിയന്ത്രണങ്ങളുടെ സിസ്റ്റത്തിന്റെ സമവാക്യങ്ങളിൽ മാത്രമേ അവതരിപ്പിക്കുകയുള്ളൂ.

ഉദാഹരണം. പ്രവർത്തനം പരമാവധിയാക്കുക Z=x 1 +2x 2 -2x 3 നിയന്ത്രണങ്ങളോടെ

പരിഹാരം. നമുക്ക് ഒറിജിനൽ ലീനിയർ പ്രോഗ്രാമിംഗ് പ്രശ്നം ഒരു കാനോനിക്കൽ ഒന്നാക്കി മാറ്റാം (കാണുക (2.1.1). ഇത് ചെയ്യുന്നതിന്, ഞങ്ങൾ അധിക നോൺ-നെഗറ്റീവ് വേരിയബിളുകൾ നിയന്ത്രണങ്ങളിലേക്ക് അവതരിപ്പിക്കുന്നു. അതായത്, ആദ്യത്തെ അസമത്വത്തിലേക്ക് - വേരിയബിൾ x 4 "+" ചിഹ്നം, രണ്ടാമത്തേത് - x 5 ഒരു "-" അടയാളം (§2.2 കാണുക). നിയന്ത്രണങ്ങളുടെ സംവിധാനം ഇനിപ്പറയുന്ന രൂപത്തിലായിരിക്കും:

നമുക്ക് ഈ സിസ്റ്റം വെക്റ്റർ രൂപത്തിൽ എഴുതാം: എ 1 x 1 +എ 2 x 2 +എ 3 x 3 +എ 4 x 4 +എ 5 x 5 =ബി, എവിടെ

ഈ നിയന്ത്രണ സംവിധാനത്തിൽ യൂണിറ്റ് അടിസ്ഥാനമില്ലെന്ന് വ്യക്തമാണ്. ഇതിനർത്ഥം വെക്റ്ററുകൾക്കിടയിൽ എന്നാണ് എ ജെആവശ്യമായ മൂന്ന് യൂണിറ്റ് വെക്‌ടറുകളൊന്നുമില്ല, അവയ്ക്ക് അടിസ്ഥാനം ആവശ്യമാണ് ആർ 3. എന്നിരുന്നാലും, വെക്റ്റർ ശ്രദ്ധിക്കുക എ 4 അടിസ്ഥാനത്തിന്റെ ഭാഗമാണ്. ഇത് അടിസ്ഥാന വേരിയബിളുമായി യോജിക്കുന്നു x 4 . രണ്ട് യൂണിറ്റ് വെക്റ്ററുകൾ കൂടി കണ്ടെത്തേണ്ടത് ആവശ്യമാണ്. ഇത് ചെയ്യുന്നതിന്, ഞങ്ങൾ കൃത്രിമ അടിസ്ഥാന രീതി പ്രയോഗിക്കുന്നു. അടിസ്ഥാന വേരിയബിൾ ഇല്ലാത്ത നിയന്ത്രണ സമവാക്യങ്ങളിലേക്ക് നമുക്ക് കൃത്രിമ വേരിയബിളുകൾ അവതരിപ്പിക്കാം. x 4 കൂടാതെ ഇനിപ്പറയുന്ന സഹായ പ്രശ്നം (AP) നിർമ്മിക്കുക:

എഫ്=-w 1 -w 2 ®പരമാവധി

എവിടെ w 1 , w 2 - കൃത്രിമ വേരിയബിളുകൾ. വെക്റ്റർ രൂപത്തിൽ വായു മലിനീകരണ നിയന്ത്രണ സംവിധാനത്തിന് ഇനിപ്പറയുന്ന രൂപമുണ്ട്: എ 1 x 1 +എ 2 x 2 +എ 3 x 3 +എ 4 x 4 +എ 5 x 5 +എ 6 w 1 +എ 7 w 2 =ബി, എവിടെ വെക്റ്ററുകൾ എ ജെ , ജെ=1,2,3,4,5 മുകളിൽ പറഞ്ഞിരിക്കുന്ന അതേ രീതിയിൽ നിർവചിച്ചിരിക്കുന്നു, കൂടാതെ . അങ്ങനെ, വെക്റ്ററുകൾ എ 4 , എ 6 , എ 7 ഒരു അടിസ്ഥാനമായി മാറുന്നു ആർ 3 അവ അടിസ്ഥാന വേരിയബിളുകളുമായി (ബിപി) യോജിക്കുന്നു - x 4 , w 1 , w 2. മറ്റെല്ലാ വേരിയബിളുകളും, അതായത് x 1 , x 2 , x 3 , x 5 പേരെ സ്വതന്ത്രരായി (എസ്പി) പ്രഖ്യാപിച്ചു. അടുത്തതായി, എയർ ഇൻടേക്കിന് ഞങ്ങൾ സാധാരണ സിംപ്ലക്സ് രീതി പ്രയോഗിക്കുന്നു. മുമ്പത്തെപ്പോലെ, §5.1 കാണുക, ഫ്രീ വേരിയബിളുകൾക്ക് പൂജ്യത്തിന് തുല്യമായ മൂല്യങ്ങൾ നൽകി പ്രാരംഭ റഫറൻസ് ഡിസൈൻ ലഭിക്കും. ഈ സാഹചര്യത്തിൽ, അടിസ്ഥാന വേരിയബിളുകൾ സ്വതന്ത്ര ഗുണകങ്ങളുടെ നിരയുടെ അനുബന്ധ വരിയിലെ സംഖ്യകൾക്ക് തുല്യമായ മൂല്യങ്ങൾ എടുക്കുന്നു. IN, അതാണ് x 1 =x 2 =x 3 =x 5 =0¸ എ x 4 =8, w 1 =4, w 2 =12. പ്രാരംഭ റഫറൻസ് പ്ലാനിന് അനുയോജ്യമായ ഒരു സിംപ്ലക്സ് പട്ടിക ഞങ്ങൾ നിർമ്മിക്കുന്നു:

എസ്പി ബിപി.	x 1	x 2	x 3	x 5	ബി
x 4		-3
w 1				-1
w 2		-2
എഫ്	-4		-3		-16

ഒപ്റ്റിമൽ സിംപ്ലക്‌സ് ടേബിൾ ലഭിക്കുന്നതുവരെ അല്ലെങ്കിൽ പരിഹരിക്കാനാകാത്തത് ലഭിക്കുന്നതുവരെ സിംപ്ലക്സ് രീതിയുടെ ആവശ്യമായ പരിവർത്തനങ്ങൾ ഈ പട്ടിക ഉപയോഗിച്ച് ഞങ്ങൾ നടപ്പിലാക്കുന്നു (§5.1 കാണുക). ഞങ്ങളുടെ കാര്യത്തിൽ, ഇതിനകം രണ്ടാം ഘട്ടത്തിൽ നമുക്ക് ഇനിപ്പറയുന്ന സിംപ്ലക്സ് പട്ടിക ലഭിക്കും:

എസ്പി ബിപി.	w 1	x 2	x 3	w 2	ബി
x 4	-0,5	-3	-0,5	-0,5
x 1	0,25		0,75	0,25
x 5	-0,75	-2
എഫ്

ഈ പട്ടിക EOI-ക്ക് അനുയോജ്യമാകും. അതേ സമയം, എല്ലാ കൃത്രിമ വേരിയബിളുകളും സ്വതന്ത്രവും പരമാവധി ആയിത്തീർന്നു എഫ്=0. ഡമ്മി വേരിയബിളുകൾക്കും അവസാന നിരയ്ക്കും അനുയോജ്യമായ നിരകൾ ക്രോസ് ചെയ്യുക, യഥാർത്ഥ ഒബ്ജക്റ്റീവ് ഫംഗ്ഷൻ ഉപയോഗിച്ച് എസ്റ്റിമേറ്റുകളുടെ ഒരു പുതിയ നിര നൽകുക Z(എക്സ്), ഒറിജിനൽ എൽപി പ്രശ്‌നത്തിന് ഞങ്ങൾ പ്രാരംഭ സിംപ്ലക്സ് പട്ടിക നേടുന്നു:

എസ്പി ബിപി.	x 2	x 3	ബി
x 4	-3	-0,5
x 1		0,75
x 5	-2
Z	-2	2,75

അവസാന പട്ടിക വിശകലനം ചെയ്ത ശേഷം, വസ്തുനിഷ്ഠമായ പ്രവർത്തനത്തിന്റെ പരിധിയില്ലാത്തതിനാൽ യഥാർത്ഥ എൽപി പ്രശ്‌നത്തിന് പരിഹാരമില്ലെന്ന് ഞങ്ങൾ നിഗമനം ചെയ്യുന്നു.

ഉദാഹരണം. പ്രവർത്തനം ചെറുതാക്കുക നിയന്ത്രണങ്ങൾക്ക് കീഴിൽ

ഞങ്ങൾ അധിക നോൺ-നെഗറ്റീവ് വേരിയബിളുകൾ അവതരിപ്പിക്കുകയും , , , വസ്തുനിഷ്ഠമായ പ്രവർത്തനത്തിന്റെ പരമാവധി കണ്ടെത്തുന്നതിനുള്ള പ്രശ്നത്തിലേക്ക് നീങ്ങുകയും ചെയ്താൽ, യഥാർത്ഥ പ്രശ്നം ഫോം എടുക്കും:

അടിസ്ഥാന പരിഹാരത്തിന് (അനുവദനീയമായ പ്ലാൻ) ഫോം ഉണ്ടായിരിക്കും: , a , , w 1 =10, w 2 =5. പ്രാരംഭ റഫറൻസ് പ്ലാനിന് അനുസൃതമായി ഞങ്ങൾ എയർഫീൽഡിനായി ഒരു സിംപ്ലക്സ് പട്ടിക നിർമ്മിക്കുന്നു:

എസ്പി ബിപി.	x 1	x 2	x 3	x 4	ബി
w 1			-1
w 2				-1
x 5
x 6	-1
എഫ്	-1	-1			-15

ജോർദാൻ-ഗോസ് രീതി ഉപയോഗിച്ച് പരിവർത്തനങ്ങൾ നടത്തുന്നു, രണ്ടാം ഘട്ടത്തിൽ നമുക്ക് VZ (5.2.2) ന്റെ ഒപ്റ്റിമൽ സിംപ്ലക്സ് പട്ടിക ലഭിക്കും. ഡമ്മി വേരിയബിളുകൾക്കും അവസാന നിരയ്ക്കും അനുയോജ്യമായ നിരകൾ ക്രോസ് ചെയ്യുക, ഒബ്ജക്റ്റീവ് ഫംഗ്ഷൻ ഉപയോഗിച്ച് സ്‌കോറുകളുടെ ഒരു പുതിയ നിര നൽകുക Z 1 (എക്സ്), പ്രശ്നത്തിനുള്ള പ്രാരംഭ സിംപ്ലക്സ് ടേബിൾ ഞങ്ങൾ നേടുന്നു (5.2.1).

കൃത്രിമ അടിസ്ഥാന രീതി അൽഗോരിതത്തിന് ഇനിപ്പറയുന്ന സവിശേഷതകൾ ഉണ്ട്:

1. വിപുലീകൃത പ്രശ്നത്തിന്റെ പ്രാരംഭ റഫറൻസ് സൊല്യൂഷനിൽ ഒരു ഗുണകം ഉപയോഗിച്ച് ഒബ്ജക്റ്റീവ് ഫംഗ്ഷനിൽ ഉൾപ്പെടുത്തിയിരിക്കുന്ന കൃത്രിമ വേരിയബിളുകൾ അടങ്ങിയിരിക്കുന്നു എന്ന വസ്തുത കാരണം - എം(പരമാവധി ടാസ്ക്കിൽ) അല്ലെങ്കിൽ + എം(മിനിമം പ്രശ്നത്തിൽ), വ്യവസ്ഥകളുടെ വെക്റ്ററുകളുടെ വികാസത്തിന്റെ എസ്റ്റിമേറ്റിൽ രണ്ട് പദങ്ങളും ഉൾപ്പെടുന്നു , അവയിലൊന്ന് ആശ്രയിക്കുന്നില്ല എം, മറ്റൊന്ന് ആശ്രയിച്ചിരിക്കുന്നു എം. കാരണം എംഐക്യവുമായി താരതമ്യപ്പെടുത്തുമ്പോൾ ഏകപക്ഷീയമായി വലുത് ( എം>> 1), തുടർന്ന് കണക്കുകൂട്ടലിന്റെ ആദ്യ ഘട്ടത്തിൽ, അടിസ്ഥാനത്തിലേക്ക് കൊണ്ടുവന്ന വെക്റ്ററുകൾ കണ്ടെത്തുന്നതിന്, എസ്റ്റിമേറ്റുകളുടെ നിബന്ധനകൾ മാത്രമേ ഉപയോഗിക്കുന്നുള്ളൂ. .

2. റഫറൻസ് സൊല്യൂഷന്റെ അടിസ്ഥാനത്തിൽ ഉരുത്തിരിഞ്ഞ കൃത്രിമ വേരിയബിളുകളുമായി ബന്ധപ്പെട്ട വെക്റ്ററുകൾ പരിഗണനയിൽ നിന്ന് ഒഴിവാക്കിയിരിക്കുന്നു.

3. കൃത്രിമ വേരിയബിളുകളുമായി ബന്ധപ്പെട്ട എല്ലാ വെക്റ്ററുകളും അടിസ്ഥാനത്തിൽ നിന്ന് ഒഴിവാക്കിയ ശേഷം, ആശ്രയിക്കാത്ത എസ്റ്റിമേറ്റ് ഉപയോഗിച്ച് സാധാരണ സിംപ്ലക്സ് രീതി ഉപയോഗിച്ച് കണക്കുകൂട്ടൽ തുടരുന്നു. എം.

4. വിപുലീകൃത പ്രശ്നം പരിഹരിക്കുന്നതിൽ നിന്ന് യഥാർത്ഥ പ്രശ്നം പരിഹരിക്കുന്നതിലേക്കുള്ള മാറ്റം മുകളിൽ തെളിയിക്കപ്പെട്ട 4.1-4.3 സിദ്ധാന്തങ്ങൾ ഉപയോഗിച്ചാണ് നിർമ്മിച്ചിരിക്കുന്നത്.

ഉദാഹരണം 4.4.കൃത്രിമ അടിസ്ഥാന രീതി ഉപയോഗിച്ച് ഒരു ലീനിയർ പ്രോഗ്രാമിംഗ് പ്രശ്നം പരിഹരിക്കുക

.

പരിഹാരം. നമുക്ക് ഒരു വിപുലീകൃത ടാസ്ക് സൃഷ്ടിക്കാം. നിയന്ത്രണ സംവിധാനത്തിന്റെ സമവാക്യങ്ങളുടെ ഇടത് വശത്തേക്ക് ഒരു ഗുണകം (എല്ലായ്പ്പോഴും) +1 ഉള്ള നോൺ-നെഗറ്റീവ് കൃത്രിമ വേരിയബിളുകൾ ഞങ്ങൾ അവതരിപ്പിക്കുന്നു. സമവാക്യങ്ങളുടെ വലതുവശത്ത് അവതരിപ്പിച്ച കൃത്രിമ വേരിയബിളുകൾ എഴുതുന്നത് സൗകര്യപ്രദമാണ്. ആദ്യ സമവാക്യത്തിൽ നമ്മൾ പ്രവേശിക്കുന്നു, രണ്ടാമത്തേതിൽ - . ഈ പ്രശ്നം പരമാവധി കണ്ടെത്തുന്നതിനുള്ള ഒരു പ്രശ്നമാണ്, അതിനാൽ അവ ഒരു ഗുണകം ഉപയോഗിച്ച് ഒബ്ജക്റ്റീവ് ഫംഗ്ഷനിലേക്ക് അവതരിപ്പിക്കുന്നു - എം. നമുക്ക് ലഭിക്കുന്നു

പ്രശ്നത്തിന് ഒരു പ്രാഥമിക റഫറൻസ് പരിഹാരമുണ്ട് യൂണിറ്റ് അടിസ്ഥാനത്തിൽ .

റഫറൻസ് സൊല്യൂഷനും റഫറൻസ് സൊല്യൂഷനിലെ ഒബ്ജക്റ്റീവ് ഫംഗ്‌ഷന്റെ മൂല്യവും അടിസ്ഥാനമാക്കി ഞങ്ങൾ കണ്ടീഷൻ വെക്‌ടറുകളുടെ എസ്റ്റിമേറ്റ് കണക്കാക്കുന്നു.

.
.

ഞങ്ങൾ ഉറവിട ഡാറ്റ ഒരു സിംപ്ലക്സ് പട്ടികയിൽ രേഖപ്പെടുത്തുന്നു (പട്ടിക 4.6).

പട്ടിക 4.6

അതേ സമയം, എസ്റ്റിമേറ്റുകളും കണക്കുകൂട്ടലുകളുടെ സൗകര്യാർത്ഥം, ഞങ്ങൾ രണ്ട് വരികളിൽ എഴുതുന്നു: ആദ്യത്തേതിൽ - ആശ്രയിക്കാത്ത നിബന്ധനകൾ എം, രണ്ടാമത്തേതിൽ - നിബന്ധനകൾ , ഇതിനെ ആശ്രയിച്ച് എം. മൂല്യങ്ങൾ ഇല്ലാതെ സൂചിപ്പിക്കാൻ സൗകര്യപ്രദമാണ് എം, മനസ്സിൽ വെച്ചുകൊണ്ട്, എന്നിരുന്നാലും, അത് അവിടെയുണ്ട്.

പരമാവധി പ്രശ്‌നത്തിന് നെഗറ്റീവ് എസ്റ്റിമേറ്റ് ഉള്ളതിനാൽ പ്രാരംഭ പിന്തുണാ പരിഹാരം അനുയോജ്യമല്ല. റഫറൻസ് സൊല്യൂഷന്റെ അടിസ്ഥാനത്തിൽ നൽകിയ വെക്റ്ററിന്റെ എണ്ണവും അടിസ്ഥാനത്തിൽ നിന്ന് ഉരുത്തിരിഞ്ഞ വെക്റ്ററിന്റെ എണ്ണവും ഞങ്ങൾ തിരഞ്ഞെടുക്കുന്നു. ഇത് ചെയ്യുന്നതിന്, അടിസ്ഥാനത്തിലേക്ക് നെഗറ്റീവ് എസ്റ്റിമേറ്റ് ഉള്ള ഓരോ വെക്റ്ററുകളും അവതരിപ്പിക്കുമ്പോൾ ഒബ്ജക്റ്റീവ് ഫംഗ്ഷന്റെ ഇൻക്രിമെന്റുകൾ ഞങ്ങൾ കണക്കാക്കുകയും ഈ ഇൻക്രിമെന്റിന്റെ പരമാവധി കണ്ടെത്തുകയും ചെയ്യുന്നു. ഈ സാഹചര്യത്തിൽ, എസ്റ്റിമേറ്റുകളുടെ നിബന്ധനകൾ (ഇല്ലാതെ എം) കുറഞ്ഞത് ഒരു ടേമെങ്കിലും അവഗണിക്കപ്പെടുന്നു (കൂടെ എം) പൂജ്യത്തിൽ നിന്ന് വ്യത്യസ്തമായിരിക്കില്ല. ഇക്കാര്യത്തിൽ, എസ്റ്റിമേറ്റുകളുടെ നിബന്ധനകളുള്ള ലൈൻ ലൈൻ ഉള്ളിടത്തോളം പട്ടികയിൽ ഉണ്ടാകണമെന്നില്ല . ഞങ്ങൾ കണ്ടെത്തുന്നു കെ= 3.

മൂന്നാമത്തെ നിരയിൽ "", ഞങ്ങൾ രണ്ടാമത്തെ വരിയിലെ കോഫിഫിഷ്യന്റ് 1 പരിഹരിക്കുന്ന ഘടകമായി തിരഞ്ഞെടുത്ത് ജോർദാൻ പരിവർത്തനം നടത്തുന്നു.

അടിസ്ഥാനത്തിൽ നിന്ന് ഉരുത്തിരിഞ്ഞ വെക്റ്റർ പരിഗണനയിൽ നിന്ന് ഒഴിവാക്കിയിരിക്കുന്നു (ക്രോസ് ഔട്ട്). ഞങ്ങൾ റഫറൻസ് പരിഹാരം നേടുന്നു അടിസ്ഥാനത്തിൽ (പട്ടിക 4.7). നെഗറ്റീവ് എസ്റ്റിമേറ്റ് ഉള്ളതിനാൽ പരിഹാരം ഒപ്റ്റിമൽ അല്ല = — 1.

പട്ടിക 4.7

"" കോളത്തിൽ ഞങ്ങൾ പോസിറ്റീവ് എലമെന്റിനെ മാത്രമേ പരിഹരിക്കുന്നുള്ളൂ, പുതിയ ഒരു റഫറൻസ് സൊല്യൂഷനിലേക്ക് നീങ്ങുന്നു അടിസ്ഥാനത്തിൽ (പട്ടിക 4.8).

പട്ടിക 4.8

ഈ റഫറൻസ് സൊല്യൂഷനാണ് വിപുലീകൃത പ്രശ്നത്തിനുള്ള ഏറ്റവും ഒപ്റ്റിമൽ പരിഹാരം, കാരണം പരമാവധി പ്രശ്‌നത്തിൽ അടിസ്ഥാനത്തിൽ ഉൾപ്പെടുത്താത്ത എല്ലാ വെക്‌ടറുകൾക്കുമുള്ള എസ്റ്റിമേറ്റ് പോസിറ്റീവ് ആണ്. സിദ്ധാന്തം 4.1 പ്രകാരം, യഥാർത്ഥ പ്രശ്നവും ഉണ്ട് ഒപ്റ്റിമൽ പരിഹാരം, പൂജ്യം കൃത്രിമ വേരിയബിളുകൾ നിരസിച്ചുകൊണ്ട് വിപുലീകൃത പ്രശ്നത്തിന്റെ ഒപ്റ്റിമൽ പരിഹാരത്തിൽ നിന്ന് ലഭിക്കുന്നത്, അതായത്. എക്സ്* = (0,0,6,2).

ഉത്തരം:പരമാവധി Z(എക്സ്) = -10 at .

ഉദാഹരണം 4.5.കൃത്രിമ അടിസ്ഥാന രീതി ഉപയോഗിച്ച് മിശ്രിത നിയന്ത്രണങ്ങളുള്ള ഒരു ലീനിയർ പ്രോഗ്രാമിംഗ് പ്രശ്നം പരിഹരിക്കുക

പരിഹാരം. ഞങ്ങൾ ലീനിയർ പ്രോഗ്രാമിംഗ് പ്രശ്നം കുറയ്ക്കുന്നു കാനോനിക്കൽ രൂപം. ഇത് ചെയ്യുന്നതിന്, ഞങ്ങൾ യഥാക്രമം ഒന്നും മൂന്നും നിയന്ത്രണങ്ങളിൽ അധിക വേരിയബിളുകൾ അവതരിപ്പിക്കുന്നു. നമുക്ക് ലഭിക്കുന്നു

.

ഞങ്ങൾ ഒരു വിപുലീകൃത പ്രശ്നം സൃഷ്ടിക്കുന്നു, അതിനായി ഞങ്ങൾ കൃത്രിമ വേരിയബിളുകൾ യഥാക്രമം രണ്ടാമത്തെയും മൂന്നാമത്തെയും സമവാക്യങ്ങളിലേക്ക് അവതരിപ്പിക്കുന്നു. നമുക്ക് ലഭിക്കുന്നു

ഈ വിപുലീകൃത പ്രശ്നത്തിന് ഒരു പ്രാഥമിക പിന്തുണ പരിഹാരമുണ്ട്

യൂണിറ്റ് അടിസ്ഥാനത്തിൽ , . റഫറൻസ് സൊല്യൂഷനെ അടിസ്ഥാനമാക്കി ഞങ്ങൾ കണ്ടീഷൻ വെക്റ്ററുകളുടെ എസ്റ്റിമേറ്റ് കണക്കാക്കുകയും മുമ്പത്തെ ഉദാഹരണത്തിലെ അതേ രീതിയിൽ സിംപ്ലക്സ് ടേബിളിൽ എഴുതുകയും ചെയ്യുന്നു. ഏറ്റവും കുറഞ്ഞ പ്രശ്‌നത്തിൽ വെക്‌ടറുകൾക്ക് പോസിറ്റീവ് എസ്റ്റിമേറ്റ് ഉള്ളതിനാൽ പരിഹാരം അനുയോജ്യമല്ല. പിന്തുണാ പരിഹാരങ്ങൾ മെച്ചപ്പെടുത്തുന്നു. ഓരോ റഫറൻസ് പരിഹാരത്തിനും അതിന്റേതായ പട്ടികയുണ്ട്. എല്ലാ പട്ടികകളും ഒന്നിന് താഴെ മറ്റൊന്നായി എഴുതാം, അവയെ ഒരൊറ്റ പട്ടികയിലേക്ക് സംയോജിപ്പിച്ച് (പട്ടിക 4.9).

പട്ടിക 4.9

ഒബ്ജക്റ്റീവ് ഫംഗ്ഷനിൽ വലിയ കുറവിലേക്ക് നയിക്കുന്ന വെക്റ്ററുകളിൽ ഏതാണ് അല്ലെങ്കിൽ പ്രാഥമിക പിന്തുണ പരിഹാരത്തിന്റെ അടിസ്ഥാനത്തിലേക്ക് ഞങ്ങൾ നിർണ്ണയിക്കുന്നു. ഞങ്ങൾ കണ്ടെത്തുന്നു കെ= 2, അതായത് അടിസ്ഥാനത്തിലേക്ക് വെക്റ്റർ അവതരിപ്പിക്കുന്നതാണ് നല്ലത്. അടിസ്ഥാനം ഉപയോഗിച്ച് ഞങ്ങൾ രണ്ടാമത്തെ പിന്തുണാ പരിഹാരം നേടുന്നു . ഒബ്ജക്റ്റീവ് ഫംഗ്ഷൻ . വെക്‌ടറിന് പോസിറ്റീവ് മൂല്യമുള്ളതിനാൽ ഈ പരിഹാരവും ഒപ്റ്റിമൽ അല്ല . ഞങ്ങൾ വെക്റ്ററിനെ അടിസ്ഥാനത്തിലേക്ക് പരിചയപ്പെടുത്തുന്നു, അടിസ്ഥാനം ഉപയോഗിച്ച് ഞങ്ങൾ മൂന്നാമത്തെ റഫറൻസ് പരിഹാരം നേടുന്നു . ഒബ്ജക്റ്റീവ് ഫംഗ്ഷൻ . ഈ പരിഹാരം ഒപ്റ്റിമൽ ആണ്, പക്ഷേ ഒന്നല്ല, കാരണം അടിസ്ഥാനത്തിൽ ഉൾപ്പെടുത്താത്ത വെക്റ്ററിന് പൂജ്യം മതിപ്പ് ഉണ്ട്. അതിനാൽ, ഒരു പുതിയ റഫറൻസ് സൊല്യൂഷനിലേക്ക് നീങ്ങേണ്ടത് ആവശ്യമാണ്, അത് ഒപ്റ്റിമലും ആയിരിക്കും. ഇത് ചെയ്യുന്നതിന്, നിങ്ങൾ അടിസ്ഥാനത്തിലേക്ക് വെക്റ്റർ അവതരിപ്പിക്കേണ്ടതുണ്ട്.

നമുക്ക് നാലാമത്തെ റഫറൻസ് (ഒപ്റ്റിമൽ) പരിഹാരത്തിലേക്ക് പോകാം

അടിസ്ഥാനത്തോടെ , അതിൽ . വിപുലീകരിച്ച പ്രശ്നത്തിനുള്ള ഒപ്റ്റിമൽ സൊല്യൂഷനുകൾക്ക് പൂജ്യം കൃത്രിമ വേരിയബിളുകളാണുള്ളത്. അതിനാൽ (സിദ്ധാന്തം 4.1 പ്രകാരം) യഥാർത്ഥ പ്രശ്നത്തിനും രണ്ട് ഒപ്റ്റിമൽ പരിഹാരങ്ങളുണ്ട് ഒപ്പം . യഥാർത്ഥ പ്രശ്നത്തിന്റെ ഒപ്റ്റിമൽ പരിഹാരത്തിൽ ഞങ്ങൾ അധിക വേരിയബിളുകൾ എഴുതുന്നില്ല.

ഉത്തരം: ചെയ്തത് , , , .

സിംപ്ലക്സ് എന്ന വാക്ക്

ഇംഗ്ലീഷ് അക്ഷരങ്ങളിൽ സിംപ്ലക്സ് എന്ന വാക്ക് (ട്രാൻസ്ലിറ്റ്) - സിംപ്ലക്സ്

സിംപ്ലക്സ് എന്ന വാക്കിൽ 8 അക്ഷരങ്ങൾ അടങ്ങിയിരിക്കുന്നു: e, k l m p s s

സിംപ്ലക്സ് എന്ന വാക്കിന്റെ അർത്ഥം. എന്താണ് സിംപ്ലക്സ്?

സിംപ്ലക്സ്

സിംപ്ലക്സ് (ലാറ്റിൻ സിംപ്ലക്സിൽ നിന്ന് - ലളിതം) (ഗണിതശാസ്ത്രം), ഏറ്റവും ലളിതമായ കോൺവെക്സ് പോളിഹെഡ്രോൺ നൽകിയ നമ്പർഅളവുകൾ n. n = 3 ആയിരിക്കുമ്പോൾ, ത്രിമാന ഘടന ക്രമരഹിതമായ, ടെട്രാഹെഡ്രോൺ ഉൾപ്പെടെ ഒരു ഏകപക്ഷീയമാണ്.

ടി.എസ്.ബി. - 1969-1978

ഒരേ ഹൈപ്പർപ്ലെയിനിൽ കിടക്കാത്ത n+1 ലംബങ്ങളുള്ള n-ഡൈമൻഷണൽ സ്പേസിലെ ഒരു കോൺവെക്സ് ബഹുഭുജമാണ് സിംപ്ലക്സ്. n-ഡൈമൻഷണൽ സ്‌പെയ്‌സിൽ n പോയിന്റുകൾ എല്ലായ്പ്പോഴും ഒരേ ഹൈപ്പർപ്ലെയിനിൽ കിടക്കുന്നതിനാൽ S. ഒരു പ്രത്യേക ക്ലാസായി വേർതിരിച്ചിരിക്കുന്നു.

slovar-lopatnikov.ru

ഒരേ ഹൈപ്പർപ്ലെയിനിൽ കിടക്കാത്ത n+1 ലംബങ്ങളുള്ള n-ഡൈമൻഷണൽ സ്പേസിലെ ഒരു കോൺവെക്സ് ബഹുഭുജമാണ് സിംപ്ലക്സ്. n-ഡൈമൻഷണൽ സ്‌പെയ്‌സിൽ n പോയിന്റുകൾ എല്ലായ്പ്പോഴും ഒരേ ഹൈപ്പർപ്ലെയിനിൽ കിടക്കുന്നതിനാൽ S. ഒരു പ്രത്യേക ക്ലാസായി വേർതിരിച്ചിരിക്കുന്നു.

ലോപട്നിക്കോവ്. - 2003

സബ് സിംപ്ലക്സ്

ഉപയോഗത്തിനും ഡോസിനുമുള്ള സബ് സിംപ്ലക്സ് നിർദ്ദേശങ്ങൾ: വാമൊഴിയായി, ഭക്ഷണത്തിനിടയിലോ ശേഷമോ, ആവശ്യമെങ്കിൽ, ഉറക്കസമയം മുമ്പ്. ഉപയോഗിക്കുന്നതിന് മുമ്പ് കുപ്പി ശക്തമായി കുലുക്കുക.

കൃത്രിമ അടിസ്ഥാനം ഉപയോഗിച്ച് സിംപ്ലക്സ് രീതി ഉപയോഗിച്ച് ZLP പരിഹരിക്കുന്നു

സസ്പെൻഷൻ പൈപ്പറ്റിൽ നിന്ന് ഒഴുകാൻ തുടങ്ങുന്നതിന്...

സബ് സിംപ്ലക്സ് സജീവ ചേരുവ ›› സിമെത്തിക്കോൺ* (സിമെത്തിക്കോൺ*) ലാറ്റിൻ നാമം സാബ് സിംപ്ലക്സ് എടിഎക്സ്:›› A02DA കാർമിനേറ്റീവ് മരുന്നുകൾ ഫാർമക്കോളജിക്കൽ ഗ്രൂപ്പ്...

മരുന്നുകളുടെ നിഘണ്ടു. - 2005

SAB® SIMPLEX (SAB® SIMPLEX) ഓറൽ സസ്പെൻഷൻ വെള്ള മുതൽ ചാര-വെളുപ്പ് വരെ, ചെറുതായി വിസ്കോസ്, സ്വഭാവഗുണമുള്ള പഴം (വാനില-റാസ്ബെറി) ഗന്ധം. 100 മില്ലി സിമെത്തിക്കോൺ 6.919 ഗ്രാം…

ഷോക്ക് സിംപ്ലക്സ്

CHOQUET SIMPLEX എന്നത് പ്രാദേശികമായി കോൺവെക്സ് സ്പേസ് E-യിലെ ഒരു ശൂന്യമല്ലാത്ത കോംപാക്ട് കോൺവെക്സ് സെറ്റ് X ആണ്, അതിന് ഇനിപ്പറയുന്ന ഗുണങ്ങളുണ്ട്: E സ്പേസിൽ ഒരു ഹൈപ്പർപ്ലെയ്ൻ ആയി ഉൾച്ചേർക്കുമ്പോൾ, ഒരു പ്രൊജക്റ്റിംഗ് കോൺ ഉണ്ട്.

ഷെഫീൽഡ് സിംപ്ലക്സ്

"ഷെഫീൽഡ്-സിംപ്ലക്സ്" - ലൈറ്റ് മെഷീൻ-ഗൺ കവചിത വാഹനം സായുധ സേനറഷ്യൻ സാമ്രാജ്യം. ബ്രിട്ടീഷ് കമ്പനിയായ ഷെഫീൽഡ്-സിംപ്ലക്സ് സ്വന്തം പാസഞ്ചർ കാറിന്റെ ഷാസിയെ അടിസ്ഥാനമാക്കി വികസിപ്പിച്ച...

en.wikipedia.org

നോർഡിട്രോപിൻ സിംപ്ലക്സ്

നോർഡിട്രോപിൻ സിംപ്ലെക്സ് സൂചനകൾ: വളർച്ചാ ഹോർമോണുകളുടെ കുറവ് അല്ലെങ്കിൽ വിട്ടുമാറാത്ത വൃക്കസംബന്ധമായ പരാജയം (പ്രീയുബർട്ടൽ പ്രായത്തിൽ), ഷെറെഷെവ്സ്കി-ടർണർ സിൻഡ്രോം എന്നിവ കാരണം കുട്ടികളിൽ വളർച്ചാ മാന്ദ്യം...

NORDITROPIN® SIMPLEX® (NORDITROPIN SimpleXx) സബ്ക്യുട്ടേനിയസ് അഡ്മിനിസ്ട്രേഷനുള്ള പരിഹാരം 1.5 മില്ലി (1 കാട്രിഡ്ജ്) സോമാട്രോപിൻ 10 മില്ലിഗ്രാം 1.5 മില്ലി - കാട്രിഡ്ജുകൾ (1) - കോണ്ടൂർ സെൽ പാക്കേജിംഗ് (1) - കാർഡ്ബോർഡ് പായ്ക്കുകൾ.

ഡയറക്ടറി മരുന്നുകൾ"വിദാൽ"

സ്റ്റാൻഡേർഡ് സിംപ്ലക്സ്

സ്റ്റാൻഡേർഡ് സിംപ്ലക്സ് - 1) S. s. - e i=(0,..., 1,..., 0), i=0,..., n (the യൂണിറ്റ് ഓണാണ് i-th സ്ഥലം), അതായത്.

ഗണിത വിജ്ഞാനകോശം. - 1977-1985

ഡ്യുവൽ സിംപ്ലക്സ് രീതി

ഒരു ലീനിയർ പ്രോഗ്രാമിംഗ് പ്രശ്നം പരിഹരിക്കാൻ ഡ്യുവൽ സിംപ്ലക്സ് രീതി ഉപയോഗിക്കാം, ഏത് സംഖ്യകളുമാകാം സമവാക്യങ്ങളുടെ സിസ്റ്റത്തിന്റെ സ്വതന്ത്ര നിബന്ധനകൾ. സാധാരണ നിലയിൽ സിംപ്ലക്സ് അൽഗോരിതംപ്ലാൻ എപ്പോഴും സാധുതയുള്ളതായിരിക്കണം.

en.wikipedia.org

റഷ്യന് ഭാഷ

സിംപ്ലക്സ്/.

മോർഫെമിക്-സ്പെല്ലിംഗ് നിഘണ്ടു. - 2002

പ്രഭാഷണങ്ങൾ തിരയുക

കൃത്രിമ അടിസ്ഥാന രീതി ഉപയോഗിച്ച് ഒരു പ്രശ്നം പരിഹരിക്കുന്നതിനുള്ള ഒരു ഉദാഹരണം.

ഒരു ഫംഗ്‌ഷന്റെ ഏറ്റവും കുറഞ്ഞ തുക കണ്ടെത്തുക F=-2×1+3×2 – 6×3 – x4വ്യവസ്ഥകൾ പ്രകാരം

പരിഹാരം.പ്രധാന പ്രശ്നത്തിന്റെ രൂപത്തിൽ ഈ പ്രശ്നം എഴുതാം: ഫംഗ്ഷന്റെ പരമാവധി കണ്ടെത്തുക F1=2×1 – 3×2 + 6×3 + x4വ്യവസ്ഥകൾ പ്രകാരം

അവസാന പ്രശ്നത്തിന്റെ സമവാക്യങ്ങളുടെ സിസ്റ്റത്തിൽ, അജ്ഞാതർക്കുള്ള ഗുണകങ്ങളുടെ വെക്റ്ററുകൾ പരിഗണിക്കുക:

A1= A2= എ 3= എ 4= എ 5= എ 6=

വെക്റ്ററുകൾക്കിടയിൽ A1,…, എ 6 രണ്ടെണ്ണം മാത്രം ( എ 4 ഒപ്പം എ 5). അതിനാൽ, നിയന്ത്രണ സംവിധാനത്തിന്റെ മൂന്നാമത്തെ സമവാക്യത്തിന്റെ ഇടതുവശത്ത് ഞങ്ങൾ ഒരു അധിക നോൺ-നെഗറ്റീവ് വേരിയബിൾ ചേർക്കുന്നു. x 7 ഒപ്പം ഫംഗ്ഷൻ പരമാവധിയാക്കുന്നതിനുള്ള വിപുലമായ പ്രശ്നം പരിഗണിക്കുക

F=2×1 – 3×2 + 6×3 + x4 – Mx7

വ്യവസ്ഥകൾ പ്രകാരം

വിപുലീകൃത പ്രശ്നത്തിന് ഒരു റഫറൻസ് പ്ലാൻ X=(0; 0; 0; 24; 22; 0; 10) ഉണ്ട്, മൂന്ന് യൂണിറ്റ് വെക്റ്ററുകളുടെ ഒരു സിസ്റ്റം നിർവ്വചിക്കുന്നു: എ 4 , A5 , A7 .

പട്ടിക 1

ഐ	അടിസ്ഥാനം	Сσ	A0	-3	—എം
A1	A2	A3	A4	A5	A6	P7
A4	-2
A5
A7	—എം	-1	-1
എം+1			-8
എം+2			-10	-1	-2

ഞങ്ങൾ അഞ്ച് വരികൾ അടങ്ങുന്ന ആവർത്തന I യുടെ പട്ടിക (1) സമാഹരിക്കുന്നു. നാലാമത്തെയും അഞ്ചാമത്തെയും വരികൾ പൂരിപ്പിക്കുന്നതിന് ഞങ്ങൾ കണ്ടെത്തുന്നു എഫ് 0, വ്യത്യാസ മൂല്യങ്ങൾ zj - cj(j=):

എഫ് 0 = 24-10M;

z1-c1= 0–എം;

z2-c2 = 4+എം;

z3-c3= –8–2എം;

z4-c4=0+എം;

z5-c5=0+എം;

z6-c6= 0+എം;

z7-c7=0+എം;

മൂല്യങ്ങൾ എഫ് 0 ഒപ്പം zj-cjരണ്ട് പദങ്ങൾ ഉൾക്കൊള്ളുന്നു, അവയിലൊന്ന് അടങ്ങിയിരിക്കുന്നു എം, മറ്റേത് അല്ല.

ആവർത്തന പ്രക്രിയയുടെ സൗകര്യാർത്ഥം, ഉൾപ്പെടുന്ന സംഖ്യ എം, അഞ്ചാമത്തെ വരിയിൽ എഴുതുക, കൂടാതെ അടങ്ങാത്ത പദം എം, – നാലാമത്തെ വരിയിൽ.

വെക്റ്ററുകളുടെ നിരകളിൽ പട്ടിക 1 ന്റെ അഞ്ചാമത്തെ വരിയിൽ എജെ (ജെ= ) രണ്ട് നെഗറ്റീവ് സംഖ്യകളുണ്ട് (-1 ഒപ്പം -2). ഈ സംഖ്യകളുടെ സാന്നിധ്യം വിപുലീകൃത പ്രശ്നത്തിനുള്ള ഈ റഫറൻസ് പ്ലാൻ അനുയോജ്യമല്ലെന്ന് സൂചിപ്പിക്കുന്നു. വിപുലീകരിച്ച പ്രശ്നത്തിന്റെ പുതിയ റഫറൻസ് പ്ലാനിലേക്ക് പോകാം.

കൃത്രിമ അടിസ്ഥാന രീതി.

ഞങ്ങൾ വെക്റ്ററിനെ അടിസ്ഥാനത്തിലേക്ക് പരിചയപ്പെടുത്തുന്നു A3. അടിസ്ഥാനത്തിൽ നിന്ന് ഒഴിവാക്കിയ വെക്റ്റർ നിർണ്ണയിക്കാൻ, ഞങ്ങൾ θ=min(22/4; 10/2)=10/2 കണ്ടെത്തുന്നു. അതിനാൽ, വെക്റ്റർ A7അടിസ്ഥാനത്തിൽ നിന്ന് ഒഴിവാക്കിയിരിക്കുന്നു. ഈ വെക്റ്ററിനെ തുടർന്നുള്ള ഏതെങ്കിലും അടിത്തറയിലേക്ക് നൽകുന്നതിൽ അർത്ഥമില്ല, അതിനാൽ ഭാവിയിൽ ഈ വെക്റ്ററിന്റെ കോളം പൂരിപ്പിക്കില്ല (പട്ടിക 2 ഉം 3 ഉം).

ഞങ്ങൾ ആവർത്തനത്തിന്റെ പട്ടിക II രചിക്കുന്നു (പട്ടിക 2). കൃത്രിമ വെക്റ്റർ അടിസ്ഥാനത്തിൽ നിന്ന് ഒഴിവാക്കിയതിനാൽ അതിൽ നാല് വരികൾ മാത്രമേ അടങ്ങിയിട്ടുള്ളൂ.

പട്ടിക 2

ഐ	അടിസ്ഥാനം	Сσ	A0	-3
A1	A2	A3	A4	A5	A6
A4	-1
A5	-1
A3	1/2	-1/2	-1/2
എം+1			-4

മേശയിൽ നിന്ന് കാണാൻ കഴിയുന്നതുപോലെ. 2, യഥാർത്ഥ പ്രശ്നത്തിന് റഫറൻസ് പ്ലാൻ ആണ് എക്സ്=(0;0;5;34;2).

ഒപ്റ്റിമലിറ്റിക്കായി ഇത് പരിശോധിക്കാം. ഇത് ചെയ്യുന്നതിന്, നാലാമത്തെ വരിയുടെ ഘടകങ്ങൾ പരിഗണിക്കുക. വെക്റ്റർ നിരയിലെ ഈ വരിയിൽ A6ഒരു നെഗറ്റീവ് നമ്പർ ഉണ്ട് (-4). തൽഫലമായി, ഈ റഫറൻസ് പ്ലാൻ ഒപ്റ്റിമൽ അല്ല, വെക്റ്റർ അവതരിപ്പിച്ചുകൊണ്ട് മെച്ചപ്പെടുത്താം A6.വെക്റ്റർ അടിസ്ഥാനത്തിൽ നിന്ന് ഒഴിവാക്കിയിരിക്കുന്നു A5. ഞങ്ങൾ ആവർത്തനത്തിന്റെ പട്ടിക III സമാഹരിക്കുന്നു.

പട്ടിക 3

അക്കങ്ങൾക്കിടയിൽ പട്ടിക 3 ന്റെ നാലാമത്തെ വരിയിൽ ∆jനെഗറ്റീവ് അല്ല. യഥാർത്ഥ പ്രശ്നത്തിന്റെ പുതിയ റഫറൻസ് പ്ലാൻ കണ്ടെത്തി എന്നാണ് ഇതിനർത്ഥം എക്സ്*=(0; 0; 11/2; 35; 0; 1) ഒപ്റ്റിമൽ ആണ്. ഈ പ്ലാൻ ഉപയോഗിച്ച്, രേഖീയ രൂപത്തിന്റെ മൂല്യം Fmax = 68.

എല്ലാ ആവർത്തനങ്ങളും തുടർച്ചയായി രേഖപ്പെടുത്തിയിരിക്കുന്ന ഒരു പട്ടിക ഉപയോഗിച്ച് ഈ പ്രശ്നത്തിനുള്ള പരിഹാരം നടപ്പിലാക്കാൻ കഴിയും.

©2015-2018 poisk-ru.ru
എല്ലാ അവകാശങ്ങളും അവയുടെ രചയിതാക്കൾക്കുള്ളതാണ്. ഈ സൈറ്റ് കർത്തൃത്വം അവകാശപ്പെടുന്നില്ല, എന്നാൽ നൽകുന്നു സ്വതന്ത്ര ഉപയോഗം.
പകർപ്പവകാശ ലംഘനവും വ്യക്തിഗത ഡാറ്റ ലംഘനവും

ഇതുവരെ, ഞങ്ങൾ പ്രശ്നം സമഗ്രമായി പരിഗണിച്ചു, അതിന്റെ പരിഹാരം സിംപ്ലക്സ് രീതിയുടെ ഏറ്റവും ലളിതമായ അൽഗോരിതം അടിസ്ഥാനമാക്കിയാണ് നടപ്പിലാക്കിയത്, കാരണം എല്ലാ നിയന്ത്രണങ്ങളും രൂപത്തിൽ കുറവോ തുല്യമോ ആയിരുന്നു. ഈ സാഹചര്യത്തിൽ, അധിക ടാസ്ക് വേരിയബിളുകൾഒരു യൂണിറ്റ് അടിസ്ഥാനം രൂപീകരിക്കുക. എന്നാൽ നിയന്ത്രണങ്ങളുടെ സമ്പ്രദായം കാനോനിക്കൽ രൂപത്തിലാണ് അവതരിപ്പിച്ചിരിക്കുന്നത്, പക്ഷേ അത് ഒരു യൂണിറ്റ് അടിസ്ഥാനത്തിലേക്ക് ചുരുക്കിയിട്ടില്ല.

അത്തരം പ്രശ്നങ്ങൾ പരിഹരിക്കുമ്പോൾ, അത് അവതരിപ്പിച്ചു കൃത്രിമ അടിസ്ഥാന രീതി. വേരിയബിളുകളുടെ എണ്ണം സമവാക്യങ്ങളുടെ എണ്ണത്തേക്കാൾ ഗണ്യമായി കവിയുമ്പോൾ ഇത് പ്രത്യേകിച്ചും സൗകര്യപ്രദമാണ്.

ഒരു ഉദാഹരണം ഉപയോഗിച്ച് കൃത്രിമ അടിസ്ഥാനം ഉപയോഗിച്ച് സിംപ്ലക്സ് രീതി ഉപയോഗിച്ച് പ്രശ്നം പരിഹരിക്കുന്നതിനുള്ള അൽഗോരിതം നമുക്ക് പരിഗണിക്കാം.

ഉദാഹരണം 1

പരമാവധി Z=4X1+2X2+X3 കണ്ടെത്തുക

3Х1+2Х2+Х3=15

Хj³0, j=1,...,3

നമുക്ക് കാനോനിക്കൽ രൂപത്തിലേക്ക് പോകാം:

X1+X2+X3-X4=8

2Х1+Х2+Х3+Х5=8

3Х1+2Х2+Х3=15

Хj³0, j=1,...,5

Zmax=4X1+2X2+X3+0×X4+0×X5

ഈ സംവിധാനംഅധിക വേരിയബിളായ X4-ന് മൈനസ് ഒന്നിന്റെ ഗുണകം ഉള്ളതിനാൽ നിയന്ത്രണങ്ങൾക്ക് യൂണിറ്റ് അടിസ്ഥാനമില്ല, കൂടാതെ മൂന്നാമത്തെ പരിമിതിയെ ഒരു സമവാക്യം പ്രതിനിധീകരിക്കുകയും അടിസ്ഥാന വേരിയബിൾ ഇല്ലാതിരിക്കുകയും ചെയ്യുന്നു. ഒരു യൂണിറ്റ് അടിസ്ഥാനം ലഭിക്കുന്നതിന്, ഞങ്ങൾ അനുബന്ധ നിയന്ത്രണങ്ങൾ അവതരിപ്പിക്കുന്നു കൃത്രിമ വേരിയബിളുകൾപോസിറ്റീവ് ഗുണകങ്ങളുള്ള y1, y2 എന്നിവ (+1).

പ്രശ്നത്തിന്റെ ഗണിതശാസ്ത്രപരമായ ഔപചാരികവൽക്കരണത്തിനായി മാത്രമാണ് കൃത്രിമ വേരിയബിളുകൾ അവതരിപ്പിക്കുന്നത് എന്നത് ശ്രദ്ധിക്കേണ്ടതാണ്. അതിനാൽ, അടിസ്ഥാന വേരിയബിളുകൾക്കിടയിൽ കൃത്രിമ വേരിയബിളുകൾ അന്തിമ പരിഹാരത്തിൽ ഉൾപ്പെടുത്താൻ കഴിയാത്ത തരത്തിലായിരിക്കണം കണക്കുകൂട്ടൽ പദ്ധതി. ഈ ആവശ്യത്തിനായി, ഒബ്ജക്റ്റീവ് ഫംഗ്ഷനിലെ കൃത്രിമ വേരിയബിളുകൾക്കായി, ഒരു കോഫിഫിഷ്യന്റ് എം അവതരിപ്പിച്ചു, ഇത് വളരെ സൂചിപ്പിക്കുന്നു. വലിയ സംഖ്യ. പ്രായോഗികമായി (പ്രത്യേകിച്ച് ഒരു കമ്പ്യൂട്ടറിൽ ഒരു പ്രശ്നം പരിഹരിക്കുമ്പോൾ), M ന് പകരം, അവർ ഒരു പ്രത്യേക വലിയ സംഖ്യ എടുക്കുന്നു, ഉദാഹരണത്തിന്, 10000. മാത്രമല്ല, ഒരു പ്രശ്നം പരമാവധി പരിഹരിക്കുമ്പോൾ, ഈ ഗുണകം ഒരു മൈനസ് ഉപയോഗിച്ച് ഒബ്ജക്റ്റീവ് ഫംഗ്ഷനിലേക്ക് പ്രവേശിക്കുന്നു. അടയാളം, കൂടാതെ കുറഞ്ഞത് പരിഹരിക്കുമ്പോൾ, ഒരു പ്ലസ് ചിഹ്നം. ഇപ്പോൾ നമ്മൾ T (M) -പ്രശ്നം പരിഹരിക്കും, ഇതിന്റെ ഒബ്ജക്റ്റീവ് ഫംഗ്ഷനിൽ Z- ടാസ്ക്കിന്റെ ഒബ്ജക്റ്റീവ് ഫംഗ്ഷനും ഒരു കോഫിഫിഷ്യന്റ് ±M ഉള്ള കൃത്രിമ വേരിയബിളുകളും അടങ്ങിയിരിക്കുന്നു, അതായത്.

T=Z-M S yi, ഒബ്ജക്റ്റീവ് ഫംഗ്‌ഷന്റെ പരമാവധി പരിഹരിക്കുമ്പോൾ ഒപ്പം

T=Z+M S y, ഒബ്ജക്റ്റീവ് ഫംഗ്‌ഷന്റെ മിനിമം സോൾവ് ചെയ്യുമ്പോൾ

ഞങ്ങളുടെ കാര്യത്തിൽ:

X1+X2+X3-X4+y1=8

2Х1+Х2+Х3+Х5=8

3Х1+2Х2+Х3+y2=15

Хj³0, j=1,...,5

പരമാവധി= 4X1+2X2+X3+0×X4+0×X5 - M(y1+y2)

ഈ പ്രശ്നം സിംപ്ലക്സ് പട്ടികകളിൽ പരിഹരിച്ചിരിക്കുന്നു, എന്നാൽ സൗകര്യാർത്ഥം ഒബ്ജക്റ്റീവ് ഫംഗ്ഷൻ 2 വരികളായി തിരിച്ചിരിക്കുന്നു:

ആദ്യ വരിയിൽ എം കോഫിഫിഷ്യന്റ് അടങ്ങിയിട്ടില്ലാത്ത കണക്കുകൾ ഞങ്ങൾ എഴുതുന്നു;

രണ്ടാമത്തെ വരിയിൽ ഓരോ ഫ്രീ വേരിയബിളിനുമുള്ള എസ്റ്റിമേറ്റുകൾ അടങ്ങിയിരിക്കുന്നു, അതിൽ കോഫിഫിഷ്യന്റ് എം അടങ്ങിയിരിക്കുന്നു.

ഈ രണ്ട് വരികളിലെ മൂലകങ്ങളുടെ (സ്കോറുകൾ) കണക്കുകൂട്ടൽ ഫോർമുല (2) അനുസരിച്ച് നടത്തുന്നു. വ്യത്യാസം മാത്രം:

Z- വരി എസ്റ്റിമേറ്റുകൾ കണക്കാക്കുമ്പോൾ, Z ഫംഗ്ഷനിൽ ഉൾപ്പെടുത്തിയിരിക്കുന്ന Cj ഗുണകങ്ങൾ കണക്കിലെടുക്കണം;

എം-ലൈൻ എസ്റ്റിമേറ്റ് കണക്കാക്കുമ്പോൾ, ഈ ഗുണകം കണക്കിലെടുക്കുന്നില്ല, കൂടാതെ എം ഒരു പൊതു ഘടകമായി എടുക്കുന്നു.

ടി-ടാസ്‌കും ഇസഡ് ടാസ്‌ക്കും തുല്യമാകുന്നതിന്, yi പൂജ്യത്തിന് തുല്യമാകേണ്ടത് ആവശ്യമാണ്. അതിനാൽ, y i പൂജ്യം അല്ലാത്തിടത്തോളം, സിംപ്ലക്സ് മെത്തേഡ് അൽഗോരിതം ഉപയോഗിച്ച് രണ്ടാമത്തെ വരിയിലെ എസ്റ്റിമേറ്റുകളെ അടിസ്ഥാനമാക്കി പരിഹരിക്കുന്ന കോളം തിരഞ്ഞെടുക്കപ്പെടുന്നു.

y i പൂജ്യത്തിന് തുല്യമായതിന് ശേഷം മാത്രമേ, ആദ്യ സൂചിക ലൈൻ ഉപയോഗിച്ച് കൂടുതൽ കണക്കുകൂട്ടൽ നടത്തൂ, അതായത്. -റെഗുലർ Z-ടാസ്ക്.

മാത്രമല്ല, കൃത്രിമ വേരിയബിൾ അടിസ്ഥാനത്തിൽ നിന്ന് ഉരുത്തിരിഞ്ഞുവരുമ്പോൾ, ഞങ്ങൾ അതിനെ സിംപ്ലെക്സ് പട്ടികയിൽ നിന്ന് പുറത്താക്കും, അടുത്ത സിംപ്ലക്സ് പട്ടികയിൽ മുമ്പത്തെ പരിഹരിക്കുന്ന കോളം ഉണ്ടാകില്ല.

എം-പ്രശ്നത്തിന്റെ ഒപ്റ്റിമൽ സൊല്യൂഷനുകളും ഇസഡ്-പ്രശ്നവും തമ്മിൽ ഒരു ബന്ധമുണ്ട്, ഇനിപ്പറയുന്നവ സ്ഥാപിച്ചു സിദ്ധാന്തം:

1. എം-പ്രശ്നത്തിനുള്ള ഒപ്റ്റിമൽ സൊല്യൂഷനിൽ എല്ലാ കൃത്രിമ വേരിയബിളുകളും (y i) പൂജ്യത്തിന് തുല്യമാണെങ്കിൽ, ഈ പരിഹാരം Z- പ്രശ്നത്തിനുള്ള ഒപ്റ്റിമൽ പരിഹാരമായിരിക്കും.

2. എം-പ്രശ്നത്തിന്റെ ഒപ്റ്റിമൽ സൊല്യൂഷനിൽ കൃത്രിമ വേരിയബിളുകളിലൊന്നെങ്കിലും പൂജ്യത്തിൽ നിന്ന് വ്യത്യസ്തമാണെങ്കിൽ, നിയന്ത്രണങ്ങളുടെ സിസ്റ്റത്തിന്റെ പൊരുത്തക്കേട് കാരണം Z- പ്രശ്‌നത്തിന് പരിഹാരമില്ല.

3. M-പ്രശ്നം പരിഹരിക്കാനാകാത്തതായി മാറുകയാണെങ്കിൽ (T®+¥ അല്ലെങ്കിൽ -¥), പരിമിതികളുടെ സിസ്റ്റത്തിന്റെ പൊരുത്തക്കേട് കാരണം അല്ലെങ്കിൽ Z എന്ന ഫംഗ്ഷൻ പരിധിയില്ലാത്തതിനാൽ യഥാർത്ഥ പ്രശ്‌നവും പരിഹരിക്കാനാവില്ല.

നമുക്ക് ആദ്യത്തെ സിംപ്ലക്സ് പട്ടിക ഉണ്ടാക്കാം. M-രീതി ഉപയോഗിച്ച് പരിഹരിക്കുമ്പോൾ, പരിഹരിക്കുന്ന കോളം M- വരിയിൽ തിരഞ്ഞെടുക്കാം യഥാർത്ഥ മൂല്യംനെഗറ്റീവ് എസ്റ്റിമേറ്റ് (പരമാവധി പരിഹരിക്കുമ്പോൾ) ഏറ്റവും വലിയ പോസിറ്റീവ് എസ്റ്റിമേറ്റ് അനുസരിച്ചല്ല (മിനിമം പരിഹരിക്കുമ്പോൾ), എന്നാൽ അടിസ്ഥാനത്തിൽ നിന്ന് Y-യെ വേഗത്തിൽ നീക്കം ചെയ്യുന്ന ഒന്ന് അനുസരിച്ച്. IN ഈ ഉദാഹരണത്തിൽ(-3) സ്കോർ ഉള്ള ഫ്രീ വേരിയബിളായ X2 ന്റെ കോളമായിരിക്കും പരിഹരിക്കുന്ന കോളം.

പട്ടിക 3.1.

ആദ്യം സിംപ്ലക്സ് ടേബിൾ

ഇസഡ്-ലൈൻ പൂരിപ്പിക്കുന്നത് ഫോർമുല (2) അനുസരിച്ച് നടക്കുന്നു:

a00 = 0 × 8– 0 = 0

a01 =0 × 2– 4 = -4

a02 =0 × 1– 2 = -2

a03 =0 × 1– 1 = -1

а02 =0 × 0– 0 = 0

എം-ലൈൻ പൂരിപ്പിക്കൽ:

а¢00 = -M × 8 + (–М) × 15 = -23M

a¢01 = -M × 1 + (–M) × 3 = -4M

а¢02 = -M × 1 + (–М) × 2= -3M

а¢03 = -എം × 1+ (–എം) × 1 = -2 എം

а¢04 = -M ×(-1)+ (–М) × 0 = 1M

ഞങ്ങൾ ഒരു പൊതു ഘടകമായി M എടുക്കുന്നു.

റെസല്യൂഷൻ ലൈനിലെ അവസാന നിരയിൽ 0 അടങ്ങിയിരിക്കുന്നു, അതിനാൽ ഫ്രീ വേരിയബിൾ X4 ന്റെ കോളം മാറ്റങ്ങളില്ലാതെ കൈമാറ്റം ചെയ്യപ്പെടുന്നു.

പട്ടിക 3.2.

രണ്ടാമത്തെ സിംപ്ലക്സ് പട്ടിക

രണ്ടാമത്തെ പട്ടികയിൽ, നമുക്ക് രണ്ട് സമാനമായ മിനിമൽ സിംപ്ലെക്സ് ബന്ധങ്ങൾ ലഭിക്കുന്നതിനാൽ, ഒരു ജീർണിച്ച പരിഹാരം ലഭിക്കും. അതിനാൽ, അടയാളം കണക്കിലെടുത്ത് പരിഹരിക്കുന്ന നിരയുടെ മൂലകങ്ങളുമായുള്ള നിരയുടെ മൂലകങ്ങളുടെ ബന്ധം ഞങ്ങൾ കണ്ടെത്തുന്നു.

പട്ടിക 3.3.

മൂന്നാമത്തെ സിംപ്ലക്സ് പട്ടിക

ഇപ്പോൾ ഞങ്ങൾ സാധാരണ സിംപ്ലക്സ് രീതി ഉപയോഗിച്ച് പരിഹരിക്കുന്നു.

പട്ടിക 3.4.

നാലാമത്തെ സിംപ്ലക്സ് പട്ടിക

സെന്റ്.പി	സി ജെ
ബി.പി.	സി.ഐ	ai0	X5	X4
X3				-1
X1
X2			-2	-1
Z

മൂല്യനിർണ്ണയ വരിയിൽ, എല്ലാ ഘടകങ്ങളും നോൺ-നെഗറ്റീവ് മൂല്യങ്ങളാണ്, അതിനാൽ ഒപ്റ്റിമൽ പരിഹാരം ലഭിക്കും:

Zmax=15 Xopt(0,7,1,0,0)

ഉദാഹരണം2

ഒബ്ജക്റ്റീവ് ഫംഗ്‌ഷന്റെ ഏറ്റവും കുറഞ്ഞ (Z®min) ലേക്ക് പ്രശ്നം പരിഹരിച്ചു. അവസാന ആവർത്തനത്തിൽ ഞങ്ങൾക്ക് ഇനിപ്പറയുന്ന പട്ടിക ലഭിച്ചു:

പട്ടിക 3.5.

ഏറ്റവും പുതിയ സിംപ്ലക്സ് പട്ടിക

സെന്റ്.പി	സി ജെ
ബി.പി.	സി.ഐ	ai0	X1	X3	X4
U1	എം	-1/2	-1/2	-1/2	-1
X5		1/2	1/2	1/2
X2		15/2	3/2	1/2
Z			-1
	എം	-1/2	-1/2	-1/2	-1

ടി-പ്രശ്നത്തിൽ, ഒരു ഒപ്റ്റിമൽ പരിഹാരം ലഭിച്ചു, കാരണം എം-വരിയിൽ കൂടുതൽ പോസിറ്റീവ് എസ്റ്റിമേറ്റുകൾ ഇല്ല, അതായത്. ഒരു പരിഹരിക്കുന്ന നിരയുടെ തിരഞ്ഞെടുപ്പ് അസാധ്യമാണ്, കൂടാതെ U1 അടിസ്ഥാനത്തിലുമാണ്. ഈ സാഹചര്യത്തിൽ, യഥാർത്ഥ പ്രശ്നത്തിന് പരിഹാരമില്ല നിയന്ത്രണ സംവിധാനത്തിന്റെ പൊരുത്തക്കേട്.