Simpleks metoda− ovo je metoda urednog nabrajanja referentnih planova (sređenost se osigurava monotonom promjenom vrijednosti funkcije cilja pri prelasku na sljedeći plan). U tom slučaju potrebno je poštovati načelo: svaki sljedeći korak treba poboljšati ili, u ekstremnim slučajevima, ne pogoršati vrijednost funkcije cilja.
Za rješavanje ZLP simpleks metoda dovodi se u kanonski oblik, t.j. Od ograničenja – nejednakosti – potrebno je napraviti ograničenja – jednakost. Da bi se to postiglo, u svako ograničenje uvodi se dodatni nenegativan faktor bilančna varijabla znakom “+” ako je znak nejednakosti “£”, i znakom “–” ako je znak nejednakosti “³”.
U funkciji cilja te dodatne varijable uključene su s nula koeficijenata, tj. unos funkcije cilja neće se promijeniti. Svaka varijabla koja ne podliježe uvjetu nenegativnosti može se predstaviti kao razlika dviju nenegativnih varijabli: .
Ako ograničenja zadatka odražavaju dostupnost i potrošnju resursa, tada je brojčana vrijednost dodatne varijable u planu zadatka, zapisana u kanonskom obliku, jednaka količini neiskorištenog resursa.
Za rješavanje problema koristit ćemo se simpleks metodom skraćene simpleksne tablice sustava linearnih jednadžbi i modificiranu Jordanovu metodu eliminacije.
1. Izrada prvog referentnog plana
Zadatak ostaje isti. Prevedimo standardni oblik sustava nejednadžbi (1) u kanonski oblik sustava jednadžbi uvođenjem dodatnih bilančnih varijabli x 3 , x 4 , x 5 ,x 6 .
 ili
ili 
U ekonomskom smislu, vrijednosti dodatnih varijabli x 3 , x 4 , x 5 utvrditi preostale sirovine nakon prodaje proizvoda.
Matrica dobivenog sustava jednadžbi ima oblik:

Vidi se da u matrici A bazni minor 4. reda je determinanta sastavljena od jediničnih koeficijenata za dodatne varijable x 3 , x 4 , x 5 ,x 6, budući da je različit od nule i jednak 1. To znači da su vektori stupaca za ove varijable linearno neovisni, tj. oblik osnova, i odgovarajuće varijable x 3 , x 4 , x 5 ,x 6 su osnovni(glavni). Varijable x 1 , x 2 će biti pozvan besplatno(neosnovni).
Ako su slobodne varijable x 1 i x 2 zadane različite vrijednosti, tada rješavanjem sustava s obzirom na osnovne varijable dobivamo beskonačan broj parcijalnih rješenja. Ako slobodnim varijablama daju samo nulte vrijednosti, tada se iz beskonačnog skupa partikularnih rješenja može birati osnovna rješenja- osnovni planovi.
Da bismo saznali mogu li varijable biti bazične, potrebno je izračunati determinantu koja se sastoji od koeficijenata tih varijabli. Ako ta determinanta nije jednaka nuli, onda te varijable mogu biti bazične.
Broj osnovnih rješenja i odgovarajući broj grupa osnovnih varijabli ne može biti veći od , gdje n– ukupan broj varijabli, r– broj osnovnih varijabli, r≤ m≤ n.
Za naš zadatak r = 4; n= 6. Zatim ![]() , tj. Moguće je 15 grupa od 4 osnovne varijable (ili 15 osnovnih rješenja).
, tj. Moguće je 15 grupa od 4 osnovne varijable (ili 15 osnovnih rješenja).
Riješimo sustav jednadžbi za osnovne varijable x 3 , x 4 , x 5 ,x 6:

Pod pretpostavkom da slobodne varijable x 1 = 0, x 2 = 0, dobivamo vrijednosti osnovnih varijabli: x 3 = 312; x 4 = 15; x 5 = 24;x 6 = –10, tj. osnovno rješenje će biti = (0; 0; 312; 15; 24; –10).
Ovo osnovno rješenje je neprihvatljivo, jer x 6 = –10 ≤ 0, a prema uvjetima ograničenja x 6 ≥ 0. Stoga umjesto varijable x 6 kao osnovu treba uzeti drugu varijablu među slobodnim x 1 ili x 2 .
Daljnje rješenje ćemo provesti koristeći skraćene simpleks tablice, popunjavajući retke prve tablice koeficijentima sustava kako slijedi (tablica 1):
Tablica 1

F-linija se zove indeks. Ispunjen je koeficijentima ciljne funkcije uzetim sa suprotnim predznakom, budući da se jednadžba funkcije može prikazati u obliku F = 0 – (– 4x 1 – 3x 2).
U rubrici besplatni članovi b i postoji negativan element b 4 = –10, tj. Rješenje sustava nije važeće. Da bi se dobilo izvedivo rješenje (referentni plan), element b 4 mora biti nenegativan.
Odaberite x 6 -niz s negativnim slobodnim članom. Ova linija sadrži negativne elemente. Odaberite bilo koji od njih, na primjer, "–1" in x 1 -stupac, i x Stupac 1 se uzima kao stupac rezolucije(utvrdit će da je varijabla x 1 prijeći će s besplatnog na osnovno).
Dijelimo besplatne članove b i na odgovarajuće elemente a je stupac rezolucije, dobivamo evaluacijski odnosiΘ ja= = (24, 15, 12, 10). Od njih biramo najmanji pozitivan (minΘ ja=10), što će odgovarati linija dopuštenja. Omogućujući niz definira varijablu x j, koji u sljedećem koraku strši iz baze i postaje slobodan. Eto zašto x Linija od 6 je linija za omogućavanje, a element "–1" je permisivni element. Zaokružimo ga. Varijable x 1 i x 6 je zamijenjeno.
Procijenjeni omjeri Θ ja u svakom retku određuju se prema pravilima:
1) Θ ja= ako b i I a je imaju različite znakove;
2) Θ ja= ∞, ako b i= 0 i a je < 0;
3) Θ ja= ∞, ako a je = 0;
4) Θ ja= 0 ako b i= 0 i a je > 0;
5) Θ ja= ako b i I a je imaju iste znakove.
Izvodimo korak modificirane Jordanove eliminacije (JEME) s razlučujućim elementom i sastavljamo novu tablicu (tablica 2) prema sljedećem pravilu:
1) umjesto razlučnog elementa (RE) postavlja se vrijednost koja je njegov inverz, tj. ;
2) elementi niza za omogućavanje podijeljeni su na RE;
3) elementi stupca rezolucije dijele se na RE i mijenja se predznak;
4) preostali elementi se nalaze prema pravilu pravokutnika:
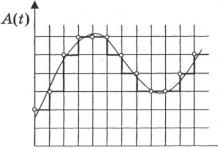
Sa stola 2 jasno je da slobodni pojmovi u b i- stupac je nenegativan, stoga se dobiva početno izvodljivo rješenje - prvi referentni plan= (10; 0; 182; 5; 4; 0). U ovom slučaju, vrijednost funkcije F() = 40. Geometrijski to odgovara vrhu F(10; 0) poligon rješenja (slika 1).
Tablica 2

2. Provjeravamo optimalnost plana. Referentni plan nije optimalan, jer u F-linija ima negativan koeficijent “–4”. Poboljšavamo plan.
3. Pronalaženje novog referentnog plana
Dopuštajući element odabiremo prema pravilu:
Biramo najmanji negativni koeficijent u F-redak “–4”, koji definira stupac rezolucije – x 6; varijabla x 6 se pretvaraju u osnovne;
Pronalaženje odnosa Θ ja, među njima odabiremo najmanju pozitivnu, koja odgovara liniji rezolucije:
min Θ ja = min(14, 5, 2, ∞) = 2, dakle, x 5-linija – omogućavanje, promjenjivo x 5 se pretvaraju u slobodne (varijable x 5 i x 6 je zamijenjeno).
Na sjecištu razlučujućeg retka i stupca nalazi se razlučujući element “2”;
Izvodimo korak SMGI i gradimo tablicu. 3 prema gornjem pravilu i dobivamo novi referentni plan = (12; 0; 156; 3; 0; 2).
Tablica 3

4. Provjera optimalnosti novog referentnog plana
Referentni plan također nije optimalan, jer u F-linija ima negativan koeficijent “–1”. Vrijednost funkcije F() = 48, što geometrijski odgovara vrhu E(12; 0) poligon rješenja (slika 1). Poboljšavamo plan.
5. Pronalaženje novog referentnog plana
x Stupac 2 je dopušten jer u F-liniji, najmanji negativni koeficijent “–1” je u x 2-stupac (Δ 2 = –1). Nalazimo najmanji Θ ja: min Θ ja = min(≈ 9, 6, ∞, 24) = 6, dakle, x 4-linijski – dopuštajući. Element rezolucije "1/2". Zamijenite varijable x 2 i x 4. Izvodimo korak SMGI i gradimo tablicu. 4, dobivamo novi referentni plan = (9; 6; 51; 0; 0; 5).
6. Provjera optimalnosti referentnog plana
U F-linija, svi koeficijenti su nenegativni, stoga je referentni plan optimalan. Geometrijski odgovara točki D(9; 6) (vidi sliku 1). Optimalni plan daje maksimalnu vrijednost funkcije cilja ![]() c.u.
c.u.
Ovdje je ručno (ne applet) rješenje dvaju problema korištenjem simplex metode (slično rješenju appleta) s detaljnim objašnjenjima kako bi se razumio algoritam za rješavanje problema korištenjem simplex metode. Prvi zadatak sadrži znakove nejednakosti samo “≤” (problem s početnom bazom), drugi može sadržavati znakove “≥”, “≤” ili “=” (problem s umjetnom bazom), različito se rješavaju.
Simpleksna metoda, rješavanje problema s početnom bazom
1)Simpleks metoda za problem s početnom bazom (svi znakovi nejednakosti ograničenja " ≤ ").
Upišimo problem kanonski obliku, tj. prepisujemo ograničenja nejednakosti u obliku jednakosti, dodajući bilanca stanja varijable:

Ovaj sustav je sustav s bazom (baze s 1, s 2, s 3, svaka od njih je uključena u samo jednu jednadžbu sustava s koeficijentom 1), x 1 i x 2 su slobodne varijable. Problemi koji se rješavaju simpleks metodom moraju imati sljedeća dva svojstva: - sustav ograničenja mora biti sustav jednadžbi s bazom; -slobodni članovi svih jednadžbi u sustavu moraju biti nenegativni.
Rezultirajući sustav je sustav s bazom i njegovi slobodni članovi su nenegativni, tako da se možemo primijeniti simpleks metoda. Kreirajmo prvu simpleks tablicu (Iteracija 0) za rješavanje problema simpleks metoda, tj. tablicu koeficijenata funkcije cilja i sustav jednadžbi za pripadajuće varijable. Ovdje "BP" znači stupac osnovnih varijabli, "Rješenje" znači stupac desnih strana jednadžbi sustava. Rješenje nije optimalno, jer postoje negativni koeficijenti u z-retku.
iteracija simpleks metode 0
|
Stav |
|||||||
Kako bismo poboljšali rješenje, prijeđimo na sljedeću iteraciju simpleks metoda, dobivamo sljedeću simpleks tablicu. Da biste to učinili, morate odabrati omogućiti stupac, tj. varijabla koja će biti uključena u bazu pri sljedećoj iteraciji simpleks metode. Odabire se prema najvećem apsolutnom negativnom koeficijentu u z-retku (u problemu maksimuma) - u početnoj iteraciji simpleks metode to je stupac x 2 (koeficijent -6).
Zatim odaberite omogućiti niz, tj. varijabla koja će napustiti bazu pri sljedećoj iteraciji simpleks metode. Odabire se najmanjim omjerom stupca “Odluka” prema odgovarajućim pozitivnim elementima stupca rezolucije (stupac “Omjer”) - u početnoj iteraciji to je red s 3 (koeficijent 20).
Permisivni element nalazi se na sjecištu razlučujućeg stupca i razlučujućeg retka, njegova ćelija je označena bojom, jednaka je 1. Stoga će pri sljedećoj iteraciji simpleks metode varijabla x 2 zamijeniti s 1 u bazi. Imajte na umu da se odnos ne traži u z-stringu; tamo se stavlja crtica "-". Ako postoje identični minimalni odnosi, odabire se bilo koji od njih. Ako su svi koeficijenti u stupcu rezolucije manji ili jednaki 0, tada je rješenje problema beskonačno.
Ispunimo sljedeću tablicu “Iteracija 1”. Dobit ćemo ga iz tablice “Iteration 0”. Cilj daljnjih transformacija je pretvoriti stupac rezolucije x2 u stupac jedinice (s jedinicom umjesto elementa rezolucije i nulama umjesto preostalih elemenata).
1) Izračunajte redak x 2 tablice "Iteracija 1". Prvo, podijelimo sve članove razrješavajućeg retka s 3 tablice "Iteracija 0" s razlučujućim elementom (u ovom slučaju je jednak 1) ove tablice, dobivamo redak x 2 u tablici "Iteracija 1" . Jer razlučujući element u ovom slučaju jednak je 1, tada će se red s 3 tablice "Iteracija 0" podudarati s retkom x 2 tablice "Iteracija 1". Red x 2 tablice Iteracije 1 dobili smo 0 1 0 0 1 20, preostali redovi tablice Iteracije 1 bit će dobiveni iz ovog retka i redaka tablice Iteracije 0 kako slijedi:
2) Izračun z-retka tablice "Iteracija 1". Umjesto -6 u prvom retku (z-redak) u stupcu x2 tablice Iteracije 0, treba postojati 0 u prvom retku tablice Iteracije 1. Da biste to učinili, pomnožite sve elemente retka x 2 tablice "Iteracija 1" 0 1 0 0 1 20 sa 6, dobit ćemo 0 6 0 0 6 120 i zbrojite ovaj red s prvim redom (z - red) tablice "Iteracija 0" -4 -6 0 0 0 0, dobivamo -4 0 0 0 6 120. U stupcu x 2 pojavljuje se nula 0, cilj je postignut. Elementi stupca rezolucije x 2 označeni su crvenom bojom.
3) Izračun retka s 1 tablice "Iteracija 1". Umjesto 1 u prvom retku tablice "Iteracija 0" trebala bi stajati 0 u tablici "Iteracija 1". Da biste to učinili, pomnožite sve elemente retka x 2 tablice "Iteracija 1" 0 1 0 0 1 20 s -1, dobijete 0 -1 0 0 -1 -20 i dodajte ovaj red sa s 1 - redom tablici "Iteration 0" 2 1 1 0 0 64, dobivamo redak 2 0 1 0 -1 44. U stupcu x 2 dobivamo traženu 0.
4) Izračunajte red s 2 u tablici "Iteracija 1". Na mjestu 3 u s 2 retku tablice "Iteracija 0" treba biti 0 u tablici "Iteracija 1". Da biste to učinili, pomnožite sve elemente retka x 2 tablice "Iteracija 1" 0 1 0 0 1 20 s -3, dobit ćemo 0 -3 0 0 -3 -60 i dodajte ovaj red sa s 1 - retkom od tablici "Iteracija 0" 1 3 0 1 0 72, dobivamo redak 1 0 0 1 -3 12. U stupcu x 2 dobiven je traženi stupac 0 u tablici “Iteracija 1”. jedinica, sadrži jednu 1, a ostatak 0.
Redovi tablice "Iteracija 1" dobivaju se prema sljedećem pravilu:
Novi red = Stari red – (Koeficijent stupca rezolucije starog retka)*(Novi redak rezolucije).
Na primjer, za z-string imamo:
Stari z-niz (-4 -6 0 0 0 0) -(-6)*Novi razrješavajući niz -(0 -6 0 0 -6 -120) =Novi z-niz (-4 0 0 0 6 120).
Za sljedeće tablice preračunavanje elemenata tablice radi se na sličan način, pa ga izostavljamo.
iteracija simpleks metode 1
|
Stav |
|||||||
Razrješavanje stupca x 1, razrješavanje reda s 2, s 2 izlazi iz baze, x 1 ulazi u bazu. Na potpuno isti način dobivamo preostale simpleks tablice dok ne dobijemo tablicu sa svim pozitivnim koeficijentima u z-retku. Ovo je znak optimalne tablice.
iteracija simpleks metode 2
|
Stav |
|||||||
Razrješavajući stupac s 3, razrješavajući red s 1, s 1 izlazi iz baze, s 3 ulazi u bazu.
iteracija simpleks metode 3
|
Stav |
|||||||
U z-retku svi koeficijenti su nenegativni, pa je dobiveno optimalno rješenje x 1 = 24, x 2 = 16, z max = 192.
| - | x 1 | + | x 2 | - | S 1 | = | 1 | ||||||||||
| x 1 | +3 | x 2 | + | S 2 | = | 15 | |||||||||||
| - | 2 | x 1 | + | x 2 | + | S 3 | = | 4 |
| - | x 1 | + | x 2 | - | S 1 | + | Dakle, određen je element koji će biti osnova. Dalje brojimo. | = | 1 | |||||||||||
| x 1 | +3 | x 2 | + | S 2 | = | 15 | ||||||||||||||
| - | 2 | x 1 | + | x 2 | + | S 3 | = | 4 |
| R 1 x 1 = 0 x 2 = 0 S 1 = 0 |
S 2 = 15 S 3 = 4 R 1 = 1 |
| x 1 | x 2 | S 1 | S 2 | S 3 | Dakle, određen je element koji će biti osnova. Dalje brojimo. | Korak #1 | Θ |
| -1 | 1 | -1 | 0 | 0 | 1 | 1 | 1: 1 = 1 |
| 1 | 3 | 0 | 1 | 0 | 0 | 15 | 15: 3 = 5 |
| -2 | 1 | 0 | 0 | 1 | 0 | 4 | 4: 1 = 4 |
| 1 | -1 | 1 | 0 | 0 | 0 | Sv. član | |
| -1 | 1 | -1 | 0 | 0 | 1 | 1 | |
| 4 | 0 | 3 | 1 | 0 | -3 | 12 | |
| -1 | 0 | 1 | 0 | 1 | -1 | 3 | |
| 0 | 0 | 0 | 0 | 0 | 1 | W - 1 |
| - | x 1 | + | x 2 | - | S 1 | = | 1 | ||||||||||
| 4 | x 1 | + | 3 | S 1 | + | S 2 | = | 12 | |||||||||
| - | x 1 | + | S 1 | + | S 3 | = | 3 |
| x 1 | x 2 | S 1 | S 2 | S 3 | Korak #1 | Θ |
| -1 | 1 | -1 | 0 | 0 | 1 | |
| 4 | 0 | 3 | 1 | 0 | 12 | 12: 4 = 3 |
| -1 | 0 | 1 | 0 | 1 | 3 | |
| 4 | 0 | 1 | 0 | 0 | W - 0 | |
| -1 | 1 | -1 | 0 | 0 | 1 | |
| 1 | 0 | 3/4 | 1/4 | 0 | 3 | |
| -1 | 0 | 1 | 0 | 1 | 3 | |
| 4 | 0 | 1 | 0 | 0 | W - 0 | |
| 0 | 1 | -1/4 | 1/4 | 0 | 4 | |
| 1 | 0 | 3/4 | 1/4 | 0 | 3 | |
| 0 | 0 | 7/4 | 1/4 | 1 | 6 | |
| 0 | 0 | -2 | -1 | 0 | F - 1 |
| F - 13 S 1 = 0 S 2 = 0 |
x 1 = 3 x 2 = 4 S 3 = 6 |
je iterativni proces usmjerenog rješavanja sustava jednadžbi u koracima, koji započinje referentnim rješenjem i, u potrazi za najboljom opcijom, kreće se duž kutnih točaka područja izvodljivog rješenja, poboljšavajući vrijednost funkcije cilja sve dok funkcija cilja dosegne optimalnu vrijednost. Svrha usluge
- . Usluga je dizajnirana za online rješavanje problema linearnog programiranja (LPP) koristeći simpleks metodu u sljedećim notnim oblicima:
- u obliku simpleks tablice (metoda Jordanove transformacije); osnovni obrazac za snimanje;
modificirana simpleks metoda; u obliku stupca; u linijskom obliku.
Sljedeći U ovom slučaju nemojte uzimati u obzir ograničenja poput x i ≥ 0. Ako u zadatku nema ograničenja za neki x i, tada se ZLP mora pretvoriti u KZLP ili koristiti ovu uslugu. Prilikom rješavanja automatski se određuje korištenje M-metoda (simpleksna metoda s umjetnom osnovom) i.dvostupanjska simpleks metoda
Sljedeće se također koristi s ovim kalkulatorom:
Grafička metoda za rješavanje ZLP
Rješenje transportnog problema
Pomoću internetske usluge možete odrediti cijenu matrične igre (donje i gornje granice), provjeriti prisutnost sedlaste točke, pronaći rješenje za mješovitu strategiju pomoću sljedećih metoda: minimaks, simpleks metoda, grafička (geometrijska ) metoda, Brownova metoda.
Ekstrem funkcije dviju varijabli
Problemi dinamičkog programiranja
Podijelite 5 homogenih serija robe između tri tržišta kako biste ostvarili najveći prihod od njihove prodaje. Prihod od prodaje na svakom tržištu G(X) ovisi o broju prodanih serija proizvoda X i prikazan je u tablici.
| Količina proizvoda X (u serijama) | Prihod G(X) | ||
| 1 | 2 | 3 | |
| 0 | 0 | 0 | 0 |
| 1 | 28 | 30 | 32 |
| 2 | 41 | 42 | 45 |
| 3 | 50 | 55 | 48 |
| 4 | 62 | 64 | 60 |
| 5 | 76 | 76 | 72 |
Algoritam Simplex metode uključuje sljedeće korake:
- Izrada prvog temeljnog plana. Prijelaz na kanonski oblik problema linearnog programiranja uvođenjem nenegativnih dodatnih bilančnih varijabli.
- Provjera optimalnosti plana. Ako postoji barem jedan koeficijent indeksne linije manji od nule, tada plan nije optimalan i potrebno ga je poboljšati.
- Određivanje vodećeg stupca i retka. Od negativnih koeficijenata indeksne linije odabire se najveći u apsolutnoj vrijednosti. Zatim se elementi stupca slobodnih članova simpleks tablice dijele na elemente istog predznaka vodećeg stupca.
- Izrada novog referentnog plana. Prijelaz na novi plan provodi se kao rezultat ponovnog izračuna simpleksne tablice metodom Jordan-Gauss.
Ako je potrebno pronaći ekstrem funkcije cilja, tada govorimo o pronalaženju minimalne vrijednosti (F(x) → min, vidi primjer rješenja minimiziranja funkcije) i maksimalne vrijednosti ((F(x ) → max, pogledajte primjer rješenja za maksimiziranje funkcije)
Ekstremno rješenje postiže se na granici područja mogućih rješenja na jednom od vrhova kutnih točaka poligona ili na segmentu između dvije susjedne kutne točke.
Temeljni teorem linearnog programiranja. Ako funkcija cilja ZLP dosegne ekstremnu vrijednost u nekoj točki u području mogućih rješenja, tada uzima tu vrijednost u kutnoj točki. Ako funkcija cilja ZLP dosegne ekstremnu vrijednost u više od jedne kutne točke, tada uzima istu vrijednost u bilo kojoj od konveksnih linearnih kombinacija tih točaka.
Suština simpleks metode. Kretanje do optimalne točke provodi se pomicanjem od jedne kutne točke do susjedne, čime se približava i brže X opt. Takva shema za nabrajanje točaka, nazvana simpleks metoda, predložio R. Danzig.
Kutne točke karakteriziraju m osnovnih varijabli, pa se prijelaz iz jedne kutne točke u susjednu može postići promjenom samo jedne osnovne varijable u bazi u varijablu iz nebaze.
Implementacija simpleks metode, zbog različitih karakteristika i formulacija problema LP, ima različite modifikacije.
Izrada simpleks tablica nastavlja se dok se ne dobije optimalno rješenje. Kako možete koristiti simpleks tablicu da odredite da je rješenje problema linearnog programiranja optimalno?
Ako zadnji redak (vrijednosti funkcije cilja) ne sadrži negativne elemente, dakle, pronaći će optimalni plan.
Napomena 1. Ako je jedna od osnovnih varijabli jednaka nuli, tada je ekstremna točka koja odgovara takvom osnovnom rješenju degenerirana. Degeneracija se javlja kada postoji dvosmislenost u izboru linije vodilje. Možda uopće nećete primijetiti degeneraciju problema ako odaberete drugu liniju kao vodič. U slučaju dvosmislenosti treba odabrati redak s najnižim indeksom kako bi se izbjeglo ponavljanje.
Opaska 2. Neka su u nekoj ekstremnoj točki sve simpleks razlike nenegativne D k ³ 0 (k = 1..n+m), tj. dobije se optimalno rješenje i postoji A k - vektor bez baze za koji je D k = 0. Tada se maksimum postiže barem u dvije točke, tj. postoji alternativni optimum. Ako ovu varijablu x k uvedemo u bazu, vrijednost funkcije cilja se neće promijeniti.
Napomena 3. Rješenje dualnog problema nalazi se u posljednjoj simpleks tablici. Posljednjih m komponenti vektora simpleksnih razlika (u stupcima varijabli bilance) optimalno su rješenje dualnog problema. Vrijednosti objektivnih funkcija izravnog i dualnog problema u optimalnim točkama podudaraju se.
Napomena 4. Pri rješavanju problema minimizacije u bazu se uvodi vektor s najvećom pozitivnom simpleks razlikom. Zatim se primjenjuje isti algoritam kao i za problem maksimizacije.
Ako je naveden uvjet "Potrebno je da se sirovine tipa III potpuno utroše", tada je odgovarajući uvjet jednakost.