Ako je svakoj točki X = (x 1, x 2, ... x n) iz skupa (X) točaka n-dimenzionalnog prostora pridružena jedna dobro definirana vrijednost varijable z, tada se kaže da je dano funkcija n varijabli z = f(x 1, x 2, ...x n) = f (X).
U ovom slučaju se pozivaju varijable x 1, x 2, ... x n nezavisne varijable ili argumenti funkcije, z - zavisna varijabla, a simbol f označava zakon dopisivanja. Skup (X) se zove domena definicije funkcije (ovo je određeni podskup n-dimenzionalnog prostora).
Na primjer, funkcija z = 1/(x 1 x 2) je funkcija dviju varijabli. Njegovi argumenti su varijable x 1 i x 2, a z je zavisna varijabla. Područje definicije je cijela koordinatna ravnina, s izuzetkom pravaca x 1 = 0 i x 2 = 0, tj. bez x- i ordinatne osi. Zamjenom bilo koje točke iz domene definicije u funkciju, prema zakonu korespondencije dobivamo određeni broj. Na primjer, uzimajući točku (2; 5), t.j. x 1 = 2, x 2 = 5, dobivamo
z = 1/(2*5) = 0,1 (tj. z(2; 5) = 0,1).
Funkcija oblika z = a 1 x 1 + a 2 x 2 + ... + a n x n + b, gdje su a 1, a 2,... i n, b konstantni brojevi, naziva se linearni. Može se smatrati zbrojem n linearnih funkcija varijabli x 1, x 2, ... x n. Pozivaju se sve ostale funkcije nelinearni.
Na primjer, funkcija z = 1/(x 1 x 2) je nelinearna, a funkcija z =
= x 1 + 7x 2 - 5 – linearno.
Bilo koja funkcija z = f (X) = f(x 1, x 2, ... x n) može se pridružiti n funkcija jedne varijable ako fiksiramo vrijednosti svih varijabli osim jedne.
Na primjer, funkcije triju varijabli z = 1/(x 1 x 2 x 3) mogu se pridružiti trima funkcijama jedne varijable. Ako fiksiramo x 2 = a i x 3 = b, tada će funkcija poprimiti oblik z = 1/(abx 1); ako fiksiramo x 1 = a i x 3 = b, tada će poprimiti oblik z = 1/(abx 2); ako fiksiramo x 1 = a i x 2 = b, tada će poprimiti oblik z = 1/(abx 3). U u ovom slučaju sve tri funkcije imaju isti oblik. Nije uvijek tako. Na primjer, ako za funkciju dviju varijabli fiksiramo x 2 = a, tada će ona poprimiti oblik z = 5x 1 a, tj. funkciju snage, a ako fiksiramo x 1 = a, tada će ona poprimiti oblik, tj. eksponencijalna funkcija.
Raspored funkcija dviju varijabli z = f(x, y) je skup točaka u trodimenzionalnom prostoru (x, y, z), čija je aplikata z povezana s apscisom x i ordinatom y funkcionalnom relacijom
z = f (x, y). Ovaj grafikon predstavlja neku površinu u trodimenzionalnom prostoru (na primjer, kao na slici 5.3).
Može se dokazati da ako je funkcija linearna (tj. z = ax + by + c), tada je njezin graf ravnina u trodimenzionalnom prostoru. Ostali primjeri 3D grafikoni Preporuča se samostalno učiti uz Kremerov udžbenik (str. 405-406).
Ako postoji više od dvije varijable (n varijabli), tada raspored funkcija je skup točaka u (n+1)-dimenzionalnom prostoru za koji se x koordinata n+1 izračunava u skladu sa zadanim funkcionalnim zakonom. Takav se graf naziva hiperpovršina(Za linearna funkcija – hiperravnina), a predstavlja i znanstvenu apstrakciju (nemoguće ju je dočarati).

Slika 5.3 – Graf funkcije dviju varijabli u trodimenzionalnom prostoru
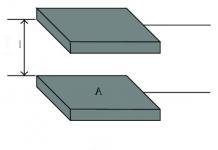
Ravna površina funkcija od n varijabli je skup točaka u n-dimenzionalnom prostoru tako da je u svim tim točkama vrijednost funkcije ista i jednaka C. Sam broj C u ovom slučaju naziva se razini.
Obično je za istu funkciju moguće konstruirati beskonačan broj ravnih ploha (koje odgovaraju različitim razinama).
Za funkciju dviju varijabli ravan ima oblik linije razine.
Na primjer, razmotrite z = 1/(x 1 x 2). Uzmimo C = 10, tj. 1/(x 1 x 2) = 10. Tada je x 2 = 1/(10x 1), tj. na ravnini će linija razine imati oblik prikazan na slici 5.4 kao puna linija. Uzimajući drugu razinu, na primjer, C = 5, dobivamo liniju razine u obliku grafa funkcije x 2 = 1/(5x 1) (prikazano točkastom linijom na slici 5.4).

Slika 5.4 - Linije funkcionalne razine z = 1/(x 1 x 2)
Pogledajmo još jedan primjer. Neka je z = 2x 1 + x 2. Uzmimo C = 2, tj. 2x 1 + x 2 = 2. Tada je x 2 = 2 - 2x 1, tj. na ravnini će linija razine imati oblik ravne crte, prikazane na slici 5.5 punom linijom. Uzimajući drugu razinu, na primjer, C = 4, dobivamo liniju razine u obliku ravne linije x 2 = 4 - 2x 1 (prikazano točkastom linijom na slici 5.5). Linija razine za 2x 1 + x 2 = 3 prikazana je na slici 5.5 kao točkasta linija.
Lako je provjeriti da će za linearnu funkciju dviju varijabli svaka linija razine biti ravna crta na ravnini, a sve linije razine biti će međusobno paralelne.

Slika 5.5 - Linije funkcionalne razine z = 2x 1 + x 2
Definiranje funkcije više varijabli
Pri razmatranju funkcija jedne varijable istaknuli smo da se pri proučavanju mnogih pojava moraju susresti funkcije dviju ili više neovisnih varijabli. Navedimo nekoliko primjera.
Primjer 1. Kvadrat S pravokutnik sa stranicama jednakih duljina x I na, izražava se formulom S = xy. Svaki par vrijednosti x I na odgovara određenoj vrijednosti površine S; S je funkcija dviju varijabli.
Primjer 2. Volumen V pravokutni paralelopiped s bridovima jednakih duljina x, na, z, izražava se formulom V= xyz. Ovdje V postoji funkcija triju varijabli x, na, z.
Primjer 3.
Raspon R let projektila ispaljenih početnom brzinom v 0 iz pištolja čija je cijev nagnuta prema horizontali pod kutom izražava se formulom  (ako zanemarimo otpor zraka). Ovdje g– ubrzanje sile teže. Za svaki par vrijednosti v 0 i ova formula daje određenu vrijednost R, tj. R je funkcija dviju varijabli v 0 i .
(ako zanemarimo otpor zraka). Ovdje g– ubrzanje sile teže. Za svaki par vrijednosti v 0 i ova formula daje određenu vrijednost R, tj. R je funkcija dviju varijabli v 0 i .
Primjer 4.
 . Ovdje I postoji funkcija četiri varijable x, na, z, t.
. Ovdje I postoji funkcija četiri varijable x, na, z, t.
Definicija 1. Ako svaki par ( x, na) vrijednosti dvije varijable neovisne jedna o drugoj x I na iz nekog područja njihove promjene D, odgovara određenoj vrijednosti količine z, onda to kažemo z postoji funkcija dvije nezavisne varijable x I na, definirana u području D.
Simbolički se funkcija dviju varijabli označava na sljedeći način:
z= f(x, g), z = F(x, g) itd.
Funkcija dviju varijabli može se odrediti, na primjer, pomoću tablice ili analitički - koristeći formulu, kao što je učinjeno u primjerima koji su gore razmotreni. Na temelju formule možete izraditi tablicu vrijednosti funkcije za neke parove vrijednosti nezavisnih varijabli. Dakle, za prvi primjer možete izraditi sljedeću tablicu:
S = xy
U ovoj tablici, na sjecištu retka i stupca koji odgovaraju određenim vrijednostima x I na, upisuje se odgovarajuća vrijednost funkcije S. Ako funkcionalna ovisnost z= f(x, g) dobiva se kao rezultat mjerenja količine z Prilikom eksperimentalnog proučavanja bilo koje pojave odmah se dobije tablica koja određuje z kao funkcija dviju varijabli. U ovom slučaju funkcija je određena samo tablicom.
Kao u slučaju jedne nezavisne varijable, funkcija dviju varijabli ne postoji, općenito govoreći, ni za jednu vrijednost x I na.
Definicija 2. Skup parova ( x, na) vrijednosti x I na, pri čemu je određena funkcija z= f(x, g), zove se domena definicije ili područje postojanja ovu funkciju.
Geometrijski je jasno prikazano područje definiranja funkcije. Ako svaki par vrijednosti x I na prikazat ćemo točkom M(x, na) u avionu Ohoo, tada će domena definiranja funkcije biti prikazana kao određeni skup točaka na ravnini. Ovu zbirku točaka također ćemo nazvati domenom definicije funkcije. Konkretno, domena definicije može biti cijela ravnina. U nastavku ćemo se uglavnom baviti područjima koja predstavljaju dijelovima aviona, omeđen linijama. Linija ograničenja ovo područje, pozvat ćemo granica područja. Točke regije koje ne leže na granici će se zvati unutarnje točke područja. Područje koje se sastoji samo od unutarnjih točaka naziva se otvoren ili otvoren. Ako rubne točke također pripadaju regiji, tada se regija naziva zatvoreno. Područje se naziva ograničenim ako postoji takva konstanta S, da je udaljenost bilo koje točke M područje od podrijetla OKO manje S, tj. | OM| < S.
Primjer 5. Odredite prirodnu domenu funkcije
z = 2x – na.
Analitički izraz 2 x – na ima smisla za bilo koju vrijednost x I na. Prema tome, prirodno područje definiranja funkcije je cijela ravnina Ohoo.
Primjer 6.
 .
.
Da bi z imao realnu vrijednost, potrebno je da ispod korijena postoji nenegativan broj, tj. x I na mora zadovoljiti nejednakost 1 – x 2 – na 2 0, odn x 2 + na 2 1.
Sve točke M(x, na), čije koordinate zadovoljavaju navedenu nejednakost, leže u krugu radijusa 1 sa središtem u ishodištu i na rubu tog kruga.
Primjer 7.
 .
.
Budući da su logaritmi definirani samo za pozitivni brojevi, tada nejednakost mora biti zadovoljena x + na> 0, ili na > x.
To znači da domena definiranosti funkcije z je polovica ravnine koja se nalazi iznad crte na = x, ne uključujući samu ravnu liniju.
Primjer 8. Površina trokuta S predstavlja baznu funkciju x i visine na: S= xy/2.
Područje definiranja ove funkcije je domena x 0, na 0 (budući da osnovica trokuta i njegova visina ne mogu biti ni negativne ni nula). Imajte na umu da se domena definicije funkcije koja se razmatra ne podudara s prirodnom domenom definicije analitičkog izraza s kojim je funkcija navedena, budući da je prirodna domena definicije izraza xy/ 2 je očito cijela ravnina Ohoo.
Definicija funkcije dviju varijabli može se lako generalizirati na slučaj tri ili više varijabli.
Definicija 3. Ako svaki razmatrani skup vrijednosti varijable x, na, z, …, u, t odgovara određenoj varijabilnoj vrijednosti w, onda ćemo nazvati w funkcija nezavisnih varijabli x, na, z, …, u, t i napiši w= F(x, na, z, …, u, t) ili w= f(x, na, z, …, u, t) i tako dalje.
Kao i za funkciju dviju varijabli, možemo govoriti o domeni definiranja funkcije tri, četiri ili više varijabli.
Tako npr. za funkciju tri promjenjivo područje Definicija je određena zbirka trojki brojeva ( x, na, z). Odmah napomenimo da svaka trojka brojeva definira određenu točku M(x, na, z) u svemiru Ohooz. Prema tome, domena definiranja funkcije triju varijabli je određeni skup točaka u prostoru.
Slično možemo govoriti o domeni definiranja funkcije četiriju varijabli u= f(x, g, z, t) kao o nekom skupu četvorki brojeva ( x, g, z, t). Međutim, domena definicije funkcije četiri odn više varijable više ne dopušta jednostavnu geometrijsku interpretaciju.
Primjer 2 prikazuje funkciju od tri varijable definirane za sve vrijednosti x, na, z.
Primjer 4 prikazuje funkciju četiri varijable.
Primjer 9. .
Ovdje w– funkcija četiriju varijabli x, na, z, I, definiran vrijednostima varijabli koje zadovoljavaju odnos:
Pojam funkcije više varijabli
Uvedimo pojam funkcije više varijabli.
Definicija 1. Neka svaka točka M iz skupa točaka ( M) Euklidski prostor Em prema nekom zakonu, određeni broj se stavlja u dopisivanje I iz numeričkog skupa U. Onda ćemo to reći na setu ( M) funkcija je dana i =f(M).Štoviše, skupovi ( M) I U nazivaju se redom domena definicije (pridjeljivanja) i domena promjene funkcije f(M).
Kao što znate, funkcija jedne varijable na = f(x) prikazan je na ravnini kao linija. U slučaju dviju varijabli, domena definicije ( M P) funkcije z = f(x, y) predstavlja skup točaka na koordinatnoj ravnini Ohoo(Slika 8.1). Koordinirati z nazvao primijeniti, a zatim se sama funkcija prikazuje kao ploha u prostoru E3 . Slično, funkcija iz T varijable

definiran na skupu ( M) Euklidski prostor Em, predstavlja hiperpovršinu u euklidskom prostoru Em+1.

Neke vrste funkcija više varijabli
Pogledajmo primjere funkcija nekoliko varijabli i pronađimo njihove domene definiranja.

E3
.
Područje definiranja ove funkcije je cijeli skup točaka ravnine ooh Raspon ove funkcije je interval X; privatno dvostruko [,] Y; privatni dvostruki [,] Z; // Popis izolinija javni popis
Za demonstraciju rada razreda, mali probna aplikacija WPF, koji gradi linije razine za funkciju oblika: z = x^2 + y^2 na rešetki 10 x 10.
MainWindow.xaml datoteka:
I kodna datoteka MainWindow.xaml.cs:
Korištenje System.Linq; koristeći System.Windows; koristeći System.Windows.Controls; koristeći System.Windows.Media; koristeći System.Windows.Shapes; prostor imena WpfLinesLevels ( ///
Rezultat testnog primjera prikazan je na slici.