Problemi linearnog programiranja (LPP). Razni oblici pisanja problema linearnog programiranja

Općenito, zadatak linearno programiranje je napisan na takav način da su ograničenja i jednadžbe i nejednadžbe, a varijable mogu biti nenegativne ili se proizvoljno mijenjati. U slučaju kada su sva ograničenja jednadžbe i sve varijable zadovoljavaju uvjet nenegativnosti, problem linearnog programiranja naziva se kanoničkim. Može se prikazati koordinatnom, vektorskom ili matričnom notacijom.

1. Problem kanonskog linearnog programiranja u koordinatnom zapisu ima oblik

U kompaktnijem obliku ovaj se problem može napisati pomoću znaka zbroja,

(1.7)

2. Problem kanonskog linearnog programiranja u vektorski zapis izgleda kao

(1.8)

Gdje ,

3. Problem kanonskog linearnog programiranja u matričnom zapisu ima oblik

(1.9)

, .

Ovdje A– matrica koeficijenata sustava jednadžbi, X– matrica-stupac problemske varijable, – matrica-stupac desnih dijelova sustava ograničenja.

Često se koriste problemi linearnog programiranja, tzv simetričan, koji u matričnom zapisu imaju oblik

(1.10)

(1.11)

1.4. Dovođenje zajednički zadatak linearno programiranje
kanonskom obliku

U većini metoda za rješavanje problema linearnog programiranja pretpostavlja se da se sustav ograničenja sastoji od jednadžbi i prirodnih uvjeta za nenegativnost varijabli. Međutim, pri sastavljanju matematičkih modela ekonomske zadaće ograničenja se uglavnom oblikuju u sustave nejednakosti, pa je potrebno moći prijeći sa sustava nejednadžbi na sustav jednadžbi. U tu svrhu dokazujemo sljedeći teorem.

Teorem 1.1. O zamjeni nejednadžbe jednadžbom. Svaka odluka nejednakosti

odgovara jedinstvenom rješenju jednadžbe

i nejednakosti

, (1.14)

i obrnuto, svako rješenje jednadžbe (1.13) i nejednadžbe (1.14) odgovara jedinstvenom rješenju nejednadžbe (1.12).

Dokaz. Neka je rješenje nejednadžbe (1.12), tada je . Označimo razliku između desne i lijeve strane ove nejednakosti s , tj.

Očito . Umjesto toga zamijenimo u jednadžbu (1.13). varijabilne vrijednosti , dobivamo

Dakle, zadovoljava jednadžbu (1.13) i nejednadžbu (1.14). To znači da je prvi dio teorema dokazan.

Neka su sada zadovoljene jednadžba (1.13) i nejednakost (1.14), tj. imamo

Odbacujući nenegativnu vrijednost na lijevoj strani posljednje jednakosti, dobivamo

tj. zadovoljava nejednakost (1.12). Teorem je dokazan.

Ako je nejednakost , tada se u nju mora uvesti dodatna nenegativna varijabla lijeva strana sa znakom minus, tj.

Nazivaju se nenegativne varijable uvedene u ograničenja nejednakosti kako bi se one pretvorile u jednadžbe dodatne varijable. Upisuju se dodatne varijable ciljna funkcija s nula koeficijenata i stoga ne utječu na njegovu vrijednost.

U slučaju kada problem ima proizvoljno mijenjanje varijabli, tada se svaka takva varijabla zamjenjuje razlikom dviju nenegativnih varijabli, tj. , Gdje I .

Ponekad je potrebno prijeći u problemu s pronalaženja minimuma na pronalaženje maksimuma ili obrnuto. Da biste to učinili, dovoljno je promijeniti predznake svih koeficijenata funkcije cilja u suprotne, au suprotnom ostaviti problem nepromijenjenim. Ovako dobivena optimalna rješenja problema maksimuma i minimuma podudaraju se, a vrijednosti funkcija cilja za optimalna rješenja razlikuju se samo predznakom.

Primjer 1.1. dovesti do kanonski oblik problem linearnog programiranja.

Otopina. Prijeđimo na problem nalaženja maksimuma funkcije cilja. Da bismo to učinili, mijenjamo predznake koeficijenata funkcije cilja. Za transformaciju druge i treće nejednadžbe sustava ograničenja u jednadžbe uvodimo nenegativne dodatne varijable (u matematičkom modelu ta je operacija označena slovom D). Varijabla se uvodi u lijevu stranu druge nejednadžbe sa znakom “+” jer nejednadžba ima oblik . Varijabla se uvodi u lijevu stranu treće nejednadžbe s predznakom “-” budući da nejednadžba ima oblik . Varijable se unose u funkciju cilja s koeficijentom jednaka nuli. Varijabla na koju nije nametnut uvjet nenegativnosti zamjenjuje se razlikom , . Problem pišemo u kanonskom obliku

U nekim slučajevima postaje nužno reducirati kanonski problem na simetrični problem. Pogledajmo primjer.

Primjer 1.2. dovesti do simetričan pogled problem linearnog programiranja

: Problemi linearnog programiranja (LPP)

1. Linearno programiranje

2. Vrste problema linearnog programiranja

3. Obrasci za evidentiranje PAP-ova

4. Kanonski oblik problema linearnog programiranja

Linearno programiranje

Linearno programiranje je grana matematičkog programiranja koja se koristi u razvoju metoda za pronalaženje ekstrema linearnih funkcija nekoliko varijabli pod linearnim dodatna ograničenja, nametnuti varijablama.

Prema vrsti problema koje rješavaju, metode LP dijele se na univerzalne i specijalne. Korištenjem univerzalne metode Svaki problem linearnog programiranja (LPP) može se riješiti. Posebni uzimaju u obzir značajke modela problema, njegovu ciljnu funkciju i sustav ograničenja.

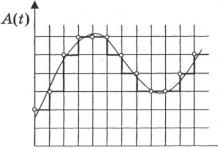
Glavna značajka problema linearnog programiranja je da se ekstrem funkcije cilja nalazi na granici područja mogućih rješenja.

Slika 1 - Ekstrem funkcije cilja

Matematički model ZLP-a zapisan je na sljedeći način:

max (ili min) Z=z(X),(1)

ODR se može prikazati sustavom linearne jednadžbe odnosno nejednakosti.

Vektor X = (x 1, x 2, .... x p) je vektor upravljanja ili učinak upravljanja.

Dopušteni plan X, u kojem kriterij optimalnosti Z=z(X) dostiže ekstremnu vrijednost, naziva se optimalnim i označava se sa X*, a ekstremna vrijednost funkcije cilja sa Z*=z(X*).

Vrste problema linearnog programiranja

Metode linearnog programiranja široko se koriste u industrijskim poduzećima pri optimizaciji proizvodnog programa, njegovoj raspodjeli po radionicama i vremenskim intervalima, pri utovaru asortimana opreme, planiranju tokova tereta, određivanju plana prometa itd.

Najčešći tip zadataka je zadatak optimalno korištenje sredstva. Neka neka proizvodna jedinica (radionica, poduzeće, udruženje itd.), na temelju tržišnih uvjeta, tehničke mogućnosti i dostupnih resursa, može proizvesti n razne vrste proizvodi poznati pod brojevima j.

Pri proizvodnji proizvoda poduzeće je ograničeno raspoloživim resursima čiju ćemo količinu označiti s m, a vektor resursa B = (b 1, b 2, ..., b t). Poznati su i tehnološki koeficijenti a ij koji pokazuju stopu utroška i-tog resursa za proizvodnju jedinice j-tog proizvoda. Izlazna učinkovitost jedinice j-i proizvodi karakteriziran profitom p j .

Potrebno je utvrditi plan proizvodnje X = (x 1, x 2, ..., x p), maksimizirajući profit poduzeća sa zadanim resursima.

Funkcija cilja izgleda ovako

pod ograničenjima

Često asortiman proizvoda utvrđuje viša organizacija, tj. njegove količine moraju biti unutar određenih granica D u j i D u j: tada se postavlja sljedeće ograničenje:

U osnovi je model problema optimalnog korištenja resursa modeli za optimizaciju godišnjeg proizvodnog programa poduzeća. Model uključuje ograničenja vremena rada opreme.

Zadržavajući isti zapis, pišemo kroz b j i c j, redom, prodajnu cijenu i trošak po jedinici jth proizvoda. Kao kriteriji optimalnosti mogu se uzeti sljedeći:

1) maksimalni profit

2) minimalni troškovi proizvodnje

3) maksimalni učinak u vrijednosnom smislu (prihod od prodaje proizvoda)

Primjer. Poduzeće može proizvesti četiri vrste proizvoda 1, 2, 3 i 4. Zajamčena je prodaja bilo kojeg volumena. Tijekom kvartala, poduzeće ima radnu snagu od 100 radnih smjena, poluproizvode težine 260 kg i alatne strojeve od 370 radnih smjena. Stope potrošnje resursa i dobit po jedinici svake vrste proizvoda prikazani su u tablici 1.

Potrebno:

a) šminkati se matematički model zadatak utvrđivanja plana proizvodnje kojim će se ostvariti maksimalna dobit;

b) riješite zadatak sa zahtjevom pakiranja tako da broj jedinica trećeg proizvoda bude 3 puta više količine prvo jedinice;

c) pronaći optimalan asortiman za dodatni uvjeti: proizvodite prvi proizvod najmanje 25 jedinica, treći - ne više od 30, a drugi i četvrti - u omjeru 1:3.

Tablica 1

Početni podaci

Matematički model problema:

funkcija cilja:

max: Z=40x 1 +50x 2 +100x 3 +80x 4

s ograničenjima:

a) za radna sredstva:

2,5x 1 +2,5x 2 +2x 3 +1,5x 4 ? 100;

za poluproizvode:

4x 1 +10x 2 +4x 3 +6x 4 ? 260;

za alatne strojeve:

8x 1 +7x 2 +4x 3 +10x 4 ? 370;

uvjet nenegativnosti:

b) dodatni zahtjev za konfiguraciju bit će izražen uvjetom

3x 1 =x 3, tj. 3x 1 x 3 =0;

c) predstavimo rubne uvjete i konfiguracijski uvjet na sljedeći način: x 1 25,

x 3?30, 3*x 2 = x 4.

Problem narudžbe ili utovara izmjenjivih grupa opreme. Radi se o o raspodjela narudžbi između m (i=1,..., m) poduzeća (radnje, strojevi, izvođači) različitih proizvodno-tehnoloških karakteristika, ali međusobno zamjenjivih u smislu ispunjavanja narudžbi. Potrebno je izraditi plan izdavanja narudžbi u kojem bi zadatak bio izvršen, a pokazatelj učinkovitosti dosegao ekstremnu vrijednost.

Formulirajmo problem matematički. Neka se n vrsta proizvoda treba proizvesti korištenjem m homogenih grupa opreme. Plan proizvodnje za svaku vrstu proizvoda određeno razdoblje dana skupom x j (j=1,2, …n). Snaga svake vrste opreme je ograničena i jednaka b i. Poznata je tehnološka matrica A=|a ij ||, gdje je a ij broj proizvedenih jedinica j-tog proizvoda u jedinici vremena i-ta oprema. Matrica C je matrica troškova, gdje su c ij troškovi povezani s outputom j-te jedinice proizvoda na i-toj opremi. X je vektor izlaznog volumena.

Model problema će imati sljedeći oblik:

ciljna funkcija - minimiziranje troškova provedbe svih naloga

s ograničenjima:

a) prema snazi opreme

b) za proizvodnju

c) uvjet nenegativnosti

Taj se problem naziva distributivni ili distribucijski problem.

Ako je za neke vrste proizvoda dopušteno prekoračenje plana, tada će ograničenje (b) imati oblik

Sljedeće se također može uzeti kao ciljna dobit:

a) maksimalan profit

b) minimalni trošak strojnog vremena

Jer Svaki model sadrži pojednostavljujuće premise; za ispravnu primjenu dobivenih rezultata potrebno je jasno razumijevanje suštine tih pojednostavljenja, što nam u konačnici omogućuje izvođenje zaključka o njihovoj prihvatljivosti ili nedopustivosti. Najznačajnije pojednostavljenje u razmatranim modelima je pretpostavka izravno proporcionalnog (linearnog) odnosa između obujma potrošnje resursa i obujma proizvodnje, koji se specificira pomoću troškovnih normi a ij . Očito, ova pretpostavka nije uvijek ispunjena. Dakle, obujmi potrošnje mnogih resursa (na primjer dugotrajne imovine) naglo se mijenjaju - ovisno o promjenama u proizvodnom programu X. Druge premise za pojednostavljenje uključuju pretpostavke o neovisnosti cijena j od obujma x j, što vrijedi samo za određene granice njihove promjene. Također je važno poznavati ta "ranjiva" područja jer ona ukazuju na temeljne smjerove za poboljšanje modela.

Obrasci za PAP evidenciju

Postoje 3 oblika bilježenja PAP-a:

1) u obliku funkcija

max(ili min)Z=,max(ili min)Z=,

2) vektorski oblik

(skalarni produkt vektora)

pod ograničenjima

A 1 x 1 +A 2 x 2 +..+A n x n = B

Gdje su vektori

C = (C 1, C 2 .. C n), X = (X 1, X 2 .. X n) i.

3) matrični oblik

pod ograničenjima

gdje je C = (c 1, c 2,...c n),

Kanonski oblik problema linearnog programiranja

Ako su sva ograničenja u problemu linearnog programiranja jednadžbe i uvjeti nenegativnosti nametnuti su svim varijablama x j, tada se to naziva problemom linearnog programiranja u kanonskom obliku ili problemom kanonskog linearnog programiranja (CLP).

pod ograničenjima

Da bi se prešlo sa ZLP na CLLP, potrebno je prijeći s ograničenja nejednakosti na ograničenja jednakosti i zamijeniti varijable koje ne poštuju uvjete nenegativnosti.

Pravila za dovođenje ZLP u kanonski oblik:

1) ako postoje ograničenja desna strana negativan, tada se ovo ograničenje treba pomnožiti s -1;

2) ako među ograničenjima postoje nejednakosti, onda se uvođenjem dodatnih nenegativnih varijabli one pretvaraju u jednakosti;

3) ako neka varijabla xk nema ograničenja predznaka, tada se u funkciji cilja i u svim ograničenjima zamjenjuje razlikom između dvije nove nenegativne varijable: xk=x * k - xl, gdje je l sumarni indeks, x * k>=, xl >=0.

Pogledajmo primjer. Dovedimo to u kanonski oblik:

U svaku jednadžbu sustava ograničenja uvedimo izravnavajuće varijable x 4, x 5, x 6. Sustav će biti napisan u obliku jednakosti, au prvoj i trećoj jednadžbi sustava ograničenja s lijeve strane s predznakom “+” upisuju se varijable x 4, x 6, a u drugoj jednadžbi x 5 upisuje se znakom “-”.

Slobodni članovi u kanonskom obliku moraju biti pozitivni, pomnožite posljednje dvije jednadžbe s -1:

U kanonskom obliku pisanja problema linearnog programiranja, sve varijable uključene u sustav ograničenja moraju biti nenegativne. Pretpostavimo da

Zamjena ovaj izraz u sustav ograničenja i funkciju cilja i pisanjem varijabli rastućim indeksnim redoslijedom, dobivamo problem linearnog programiranja prikazan u kanonskom obliku:

optimizacija simplex linearno programiranje

MP zadaci

Opći PAP nazvao <,=,>=)bi (i=1,n) (2) u skladu s xj>

Simetrično < либо = и не отрицательных переменных и задача минимизации функции (1) при linearna ograničenja u nejednakostima s predznakom > Kanonski mješoviti.

min f(x) = -max(-f(x))

<=b (5)соответствует вполне определенное решение х1…хn, xn+1 уравненияa1x1+…+anxn+xn+1=b (6) при условии что хn+1>

Geometrijska interpretacija funkcije cilja i ograničenja ZLP-a. Geometrijska formulacija ZLP.

Neka je zadan problem f=c1x1+c2x2-max (1).

a11x1+a12x2<=b1 }

am1x1+am2x2<=bm}

x1>=0, x2>=0 (3)

Plan problema (x1,x2) je točka na ravnini. Svaka nejednakost sa-mi 2 prikaza. je poluravnina. Poluravnina je konveksan skup. Konveksan naziva se skup u kojem točke segmenta koji spaja (x1 i x2) koje pripadaju tom skupu također pripadaju skupu. C-ma 2 predstavlja sjecište poluravnina. Prilikom prelaska možete dobiti:

1) konveksno poligonalno zatvoreno područje.

2) konveksno otvoreno poligonalno područje

3) jedna točka

4) prazan skup

5) greda i segment

Geometrijska interpretacija funkcije cilja: Funkcija 1 je familija paralelnih ravnih pravaca, koji se nazivaju linijama razine (pravci konstantne vrijednosti ciljne funkcije). Parcijalne derivacije funkcije u odnosu na x1 i x2 pokazuju brzinu porasta ciljne funkcije duž koordinata osi. Vektor gradijenta pokazuje smjer najbržeg porasta funkcije cilja Za problem 1-3 vektor gradijenta = (c1;c2) napušta točku (0,0) i usmjerava se na točku s koordinatama (c1;c2). Vektor gradijenta je okomit na linije razine. Sjecište poluravnina obično se naziva područje dopuštenih rješenja (ADD).

Glavni teorem LP. Shematski dijagram rješenja ZLP-a, što proizlazi iz ovog teorema.

Ako ZLP ima rješenje, tada funkcija cilja postiže ekstremnu vrijednost u barem jednoj od ekstremnih točaka planskog poliedra. Ako funkcija cilja dosegne ekstremnu vrijednost u više od jedne ekstremne točke, tada ona doseže jednu te istu vrijednost u bilo kojoj točki, koja je njihova konveksna linearna kombinacija. Kod ručnog rješavanja ZLP-a zgodno je koristiti tablični unos.

BP		SP -Xm+1 -Xm+2 -Xn
x1	b1o	b11 b12 b1n-m
x2	b2o	b21 b22 b2n-m
xm	bm	bm1 bm2 bmn-m
f	buu	bo1 bo2 bon-m

Algoritam simpleks metode.

1. model problema dovesti u kanonski oblik;

2. pronaći početni referentni plan;

3. napiši zadatak u jednostavnom obliku. stol;

5. prijeći na novi referentni plan, na novi simp. stol. Za prelazak na novi referentni plan dovoljno je jednu osnovnu varijablu zamijeniti slobodnom. Varijabla uključena u bazu i odgovarajući stupac razlučivosti određeni su najvećim apsolutno negativnim elementom f-retka. Varijabla koja isključuje iz baze i odgovarajuća razlučujuća linija određene su najmanjim simpleks omjerom, tj. odnos elemenata stupca jedinice prema odgovarajućem elementu stupca rezolucije. Simpleksni omjer je nenegativna veličina. Na sjecištu razlučujućeg retka i razlučujućeg stupca nalazi se razlučujući element u odnosu na koji simpleks transformacija sljedeći pravilo: 1. elementi dopuštajućeg niza dijele se na dopuštajući element; 2. elementi razlučnog stupca dijele se na razlučni element i mijenjaju predznak na suprotan; 3. preostali elementi tablice su presloženi prema pravilu pravokutnika:

bij bis bkj=(bkj*bis-bij*bks)/bi

Drugi teorem dualnosti.

ako jedan od dualnih problema ima optimalan plan, onda je i drugi rješiv, tj. ima optički plan. U ovom slučaju, ekstremne vrijednosti funkcija cilja se podudaraju (j=od 1 do n) Σcjxj*= (i=od 1 do m)Σbiyi* ako je u originalu. problem, funkcija cilja je neograničena na skupu planova, a zatim u dvostruki problem sustav ograničenja je nedosljedan.

Teorem o rangu TK matrice.

Rang matrice A transportnog problema je za jedan manji od broja jednadžbi: r(A)=m+n-1.

39. Algoritam za izradu početnog referentnog plana ZLP.

Kako bismo pronašli početni referentni plan, možemo predložiti sljedeće algoritam:

1. zadatak napiši u obliku Jordanove tablice tako da svi elementi stupca slobodnih članova budu nenegativni, tj. nejednakost aio>=0 (i=1,m) je bila zadovoljena. One jednadžbe u kojima su slobodni članovi negativni prvo se pomnože s -1.

		-x1….. -xn
0=	a1o	a11…. a1n
…..	…..	………………………..
0=	amo	am1…..amn
f=		-c1…. -cn

Transformirajte tablicu koristeći Jordanove korake eliminacije, zamjenjujući nule u lijevom stupcu odgovarajućim x-om. Istovremeno, na svakom koraku može se odabrati dopušteno bilo koji stupac koji sadrži barem jedan pozitivan element. Redak za razlučivanje određen je najmanjim omjerom slobodnih članova prema odgovarajućim pozitivnim elementima stupca za razlučivanje. Ako se tijekom procesa iznimke naiđe na niz 0, svi elementi što je nula, a slobodni član je različit od nule, tada sustav nema rješenja graničnih jednadžbi. Ako naiđemo na 0-redak u kojem, osim slobodnog člana, nema drugih pozitivnih elemenata, tada sustav restriktivnih jednadžbi nema nenegativnih rješenja Ako familija restriktivnih jednadžbi spojnica, tada će se nakon određenog broja koraka sve nule u lijevom stupcu zamijeniti s x i time dobiti određenu bazu, a time i odgovarajući referentni plan.

40. Algoritam za izradu optimalnog referentnog plana ZLP.

Hoov inicijalni plan podrške ispituje se radi optimalnosti.

Ako u f-redu nema negativnih elemenata (ne računajući slobodni član), -plan je optimalan. Ako f-linija također ne sadrži nulti elementi, tada postoji samo jedan optimalan plan; ako među elementima postoji barem jedna nula, tada postoji beskonačan broj optimalnih planova. Ako postoji barem jedan negativan element u f-retku, a nema pozitivnih elemenata u odgovarajućem stupcu, tada funkcija cilja nije ograničena u izvedivom području. Problem nije rješiv. Ako postoji barem jedan negativan element u f-retku, au svakom stupcu s takvim elementom postoji barem jedan pozitivan element, tada možete prijeći na novi referentni plan koji je bliži optimalnom. Da biste to učinili, stupac s negativnim elementom u f-retku uzima se kao popustljiv; Oni određuju razrješujući niz iz minimalne simpleks relacije i izvode Jordanov korak eliminacije. Dobiveni referentni plan ponovno se ispituje na optimalnost. To se ponavlja dok se ne pronađe optimalni referentni plan ili dok se ne utvrdi nerješivost problema.

Algoritam metode Gomori.

1. Simpleks metodom pronalazi se optimalni plan za problem. Ako sve komponente optimalan plan cjelina, onda je optimalna. U suprotnom prijeđite na 2. korak

2. Među necjelobrojnim komponentama treba odabrati onu s razlomački dio je najveći i, koristeći odgovarajući redak simpleks tablice, formulirajte točnu graničnu vrijednost pomoću formule

(n-m,s=1)∑ (αkm+1)Xm+1≥(βk)

3. Transformirajte formuliranu nejednadžbu u ekvivalentnu nultu jednakost i uključite je simplex tablica s necijelobrojnim optimalnim planom

4. Dobiveni prošireni problem rješava se simpleks metodom. Ako rezultirajući plan nije cijeli broj, prijeđite na korak 2.

Ako se tijekom procesa rješavanja pojavi crta s necijelobrojnim slobodnim članom i drugim cjelobrojnim koeficijentima, tada odgovarajuća jednadžba nema rješenje u cijelim brojevima. U ovom slučaju, izvorni problem je također nerješiv u cijelim brojevima. Gomorijeva metoda ima ograničenu primjenu. Uz njegovu pomoć preporučljivo je riješiti male zadatke, jer broj interakcija može biti vrlo velik.

Razni oblici ZLP zapisi (opći, kanonski, simetrični)

MP zadaci: određivanje optimalnog plana, određivanje optimalnog obujma proizvodnje, određivanje optimalne kombinacije usjeva, formiranje optimalnog paketa sredstava, maksimiziranje profita banaka i dr.

Opći ZLP zove se problem maksimizacije (minimizacije). linearna funkcija f=Σcj*xj-max(min) (1) pod linearnim ograničenjima ∑aij *xj(=<,=,>=)bi (i=1,n) (2) uz uvjet xj>=0(j=1,n1), xj-proizvoljno (j=n1+1,n)(3) gdje su cj,aij, bikonstantni brojevi .

Simetrično Oblik pisanja ZLP-a naziva se problem maksimiziranja funkcije (1) pod linearnim ograničenjima u predznačenim nejednadžbama< либо = и не отрицательных переменных и задача минимизации функции (1) при линейных ограничениях в неравенствах со знаком >ili = i nenegativne varijable. Kanonski Oblik zapisa ZLP-a naziva se problem funkcije maksimuma (1) pod linearnim ograničenjima jednakosti i nenegativnih varijabli. Svaki drugi oblik se zove mješoviti.

min f(x) = -max(-f(x))

Transformacija nejednadžbe u jednadžbu i obrnuto provodi se na temelju leme: za svako rješenje x1...xn nejednadžbe a1x1+...+anxn<=b (5)соответствует вполне определенное решение х1…хn, xn+1 уравненияa1x1+…+anxn+xn+1=b (6) при условии что хn+1>=0(7) i obrnuto. Svako rješenje x1…xn,xn+1 jednadžbe 6 i nejednadžbe 7 odgovara rješenju x1…xn nejednadžbe 5.

Za prelazak sa stražnjeg sim obrasca na stražnji kanonski obrazac, morate unijeti bilansne (izjednačujuće) varijable. Ovo se temelji na teoremu o nejednakosti: svaka se nejednakost može prikazati kao jednadžba ili jednostavna nejednadžba.

Kanonski oblik ZLP- problem linearnog programiranja oblika ax = b gdje je a matrica koeficijenata, b vektor ograničenja.

Svrha usluge. Online kalkulator dizajniran je za prijelaz JPP-a na KZLP. Dovođenje problema u kanonski oblik znači da će sva ograničenja imati oblik jednakosti uvođenjem dodatnih varijabli.
Ako nijednoj varijabli x j nije nametnuto ograničenje, tada se ono zamjenjuje razlikom dodatnih varijabli, x j = x j1 - x j2, x j1 ≥ 0, x j2 ≥ 0.

upute. Odaberite broj varijabli i broj redaka (broj ograničenja). Dobiveno rješenje sprema se u Word datoteku.

Kako svesti problem linearnog programiranja na kanonski oblik

Matematički model ZLP-a naziva se osnovni, ako su ograničenja u njemu prikazana u obliku jednadžbi pod uvjetom da su varijable nenegativne.

Matematički model je tzv kanonski, ako je njegov sustav ograničenja predstavljen u obliku sustava od m linearno neovisnih jednadžbi (rang sustava r=m), sustav se dodjeljuje jedinična osnova, definirane su slobodne varijable i funkcija cilja je izražena u terminima slobodnih varijabli. U ovom slučaju, desne strane jednadžbi su nenegativne (b i ≥ 0).

Varijable uključene u jednu od jednadžbi sustava s koeficijentom jedan i odsutne u drugim jednadžbama nazivaju se osnovne nepoznanice, i svi ostali - besplatno.

Rješenje sustava naziva se osnovni, ako su slobodne varijable u njemu jednake 0, a ima oblik:
X baze = (0, 0; b 1 , …, b m), f(X baze) = c 0

Osnovno rješenje je kutna točka skupa rješenja sustava, tj. definira vrh poligona rješenja modela. Među takvim rješenjima je i ono u kojem objektivna funkcija zauzima optimalna vrijednost.

Osnovno rješenje nazivamo referentnim ako je dopustivo, tj. sve desne strane jednadžbi sustava (ili nejednadžbi) su pozitivne b i ≥ 0.

Kompaktni oblik kanonskog modela je:
AX = b
X ≥ 0
Z = CX (maks.)

Pojam dopustivog rješenja, područje dopustivih rješenja, optimalno rješenje problema linearnog programiranja.
Definicija 1. Vektor X koji zadovoljava sustav ZLP ograničenja, uključujući uvjete nenegativnosti, ako ih ima, naziva se dopustivim rješenjem ZLP-a.
Definicija 2. Skup svih prihvatljivih rješenja čini područje prihvatljivih rješenja (ADA) PLP-a.
Definicija 3. Izvedivo rješenje za koje funkcija cilja doseže maksimum (ili minimum) naziva se optimalnim rješenjem.

Primjer br. 1. Smanjite sljedeći LP problem na kanonski oblik: F(X) = 5x 1 + 3x 2 → max pod ograničenjima:
2x 1 + 3x 2 ≤20
3x 1 + x 2 ≤15
4x 1 ≤16
3x 2 ≤12
Model je napisan u standardni obrazac. Uvedimo ravnotežne nenegativne varijable x 3 , x 4 , x 5 , x 6 , koje dodajemo na lijeve strane ograničenja nejednakosti. Sve dodatne varijable uvodimo u funkciju cilja s koeficijentima jednakima nuli:
U prvoj nejednakosti značenja (≤) uvodimo osnovnu varijablu x 3 . U 2. nejednadžbi značenja (≤) uvodimo osnovnu varijablu x 4 . U trećoj nejednadžbi uvodimo osnovnu varijablu x 5 . U 4. nejednadžbi - osnovna varijabla x 6. Dobivamo kanonski oblik modela:
2x 1 + 3x 2 + 1x 3 + 0x 4 + 0x 5 + 0x 6 = 20
3x 1 + 1x 2 + 0x 3 + 1x 4 + 0x 5 + 0x 6 = 15
4x 1 + 0x 2 + 0x 3 + 0x 4 + 1x 5 + 0x 6 = 16
0x 1 + 3x 2 + 0x 3 + 0x 4 + 0x 5 + 1x 6 = 12
F(X) = 5x 1 + 3x 2 + 0x 3 + 0x 4 + 0x 5 + 0x 6 → maks.

Primjer br. 2. Pronađite dva referentna rješenja sustava
x 1 + 2x 4 - 2x 5 = 4
x 3 + 3x 4 + x 5 = 5
x 2 + 3x 5 = 2

Upisivanje funkcije cilja i sustava ograničenja razne zadatke linearno programiranje nije isto: u nekim problemima potrebno je pronaći minimum funkcije cilja, au drugima - maksimum; u nekim slučajevima tražene varijable ovise o jednom indeksu, au drugim o dva; u nekim problemima ograničenja su navedena u obliku sustava linearne nejednakosti, au ostalima – u obliku sustava linearnih jednadžbi. U praksi je također moguće imati probleme u kojima su neka ograničenja u obliku linearnih nejednadžbi, a neka u obliku linearnih jednadžbi. Također, ne moraju svi problemi zahtijevati nenegativnost varijabli.

Uzimanje u obzir takve raznolikosti problema linearnog programiranja zahtijeva razvoj posebnih metoda za rješavanje pojedinih klasa istih. Usmjerit ćemo pažnju na učenje opća svojstva i metode linearnog programiranja napisane u takozvanom kanonskom obliku.

Ako u problemu linearnog programiranja sustav početnih ograničenja poprimi oblik jednadžbi poput

i trebate pronaći maksimum linearne funkcije cilja

tada se problem linearnog programiranja smatra napisanim u kanonskom obliku.

Svaki problem linearnog programiranja može se lako svesti na kanonski oblik. U općem slučaju, za to je dovoljno moći, prvo, svesti problem minimiziranja funkcije cilja na problem njezinog maksimiziranja, drugo, prijeći s ograničenja nejednakosti na ograničenja jednakosti, i treće, promijeniti one varijable koje su ne podliježe uvjetu nenegativnosti .

U slučaju kada treba pronaći minimum funkcije , možemo nastaviti s pronalaženjem maksimuma funkcije , budući da je sljedeća izjava istinita:
.

Ograničenje-nejednakost izvorni problem, koji izgleda kao " ", može se pretvoriti u ograničenje jednadžbe dodavanjem dodatne ne-negativne varijable na njegovu lijevu stranu i ograničenja nejednakosti oblika " ” – oduzimanjem dodatne nenegativne varijable s njegove lijeve strane.

Imajte na umu da je broj uvedenih dodatnih nenegativnih varijabli uvijek jednak broju nejednakosti u izvornom sustavu ograničenja.

Dodatne uvedene varijable imaju vrlo specifično ekonomsko značenje. Dakle, ako ograničenja izvornog problema linearnog programiranja odražavaju troškove i dostupnost proizvodnih resursa, tada numerička vrijednost dodatna varijabla pokazuje količinu odgovarajućeg neiskorištenog resursa.

Napomenimo također da ako neka varijabla ne poštuje uvjet nenegativnosti, tada se mora zamijeniti s dvije nenegativne varijable I , prihvativši
.

Primjer. Napišite sljedeći problem linearne optimizacije u kanonskom obliku: pronađite minimum funkcije
pod ograničenjima

Otopina

U ovom zadatku treba pronaći minimum funkcije cilja, a sustav ograničenja uključuje četiri nejednadžbe. Kako biste to napisali u kanonskom obliku, trebate prijeći s ograničenja nejednakosti na ograničenja jednadžbi, te također transformirati funkciju cilja.

Budući da je broj nejednakosti uključenih u sustav ograničenja problema četiri, ovaj se prijelaz mora izvesti uz uvođenje četiri dodatne nenegativne varijable. Štoviše, u drugoj i četvrtoj nejednakosti postoji znak " ", pa dodajemo dodatne varijable na njihovu lijevu stranu. U prvoj i trećoj nejednakosti stoji znak “ “, što znači da oduzimamo dodatne varijable s njihove lijeve strane.