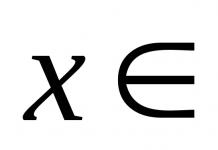Määritelmä 1

Sarja kaikista antijohdannaisista annettu toiminto Tietylle segmentille määritettyä $y=f(x)$ kutsutaan tietyn funktion $y=f(x)$ määrittelemättömäksi integraaliksi. Epämääräinen integraali merkitty symbolilla $\int f(x)dx $.

Kommentti

Määritelmä 2 voidaan kirjoittaa seuraavasti:

\[\int f(x)dx =F(x)+C.\]

Ei kaikilta irrationaalinen toiminto integraali voidaan ilmaista alkeisfunktioilla. Suurin osa näistä integraaleista voidaan kuitenkin pelkistää käyttämällä rationaalifunktioiden integraaleja, jotka voidaan ilmaista alkeisfunktioina.

$\int R\left(x,x^(m/n) ,...,x^(r/s) \right)dx $;

$\int R\left(x,\left(\frac(ax+b)(cx+d) \right)^(m/n) ,...,\left(\frac(ax+b)(cx) +d) \oikea)^(r/s) \oikea)dx $;

$\int R\left(x,\sqrt(ax^(2) +bx+c) \right)dx $.

minä

Kun löydetään integraali muotoa $\int R\left(x,x^(m/n) ,...,x^(r/s) \right)dx $, on suoritettava seuraava korvaus:

Tällä korvauksella jokainen muuttujan $x$ murtoluku ilmaistaan ​​muuttujan $t$ kokonaislukupotenssilla. Tämän seurauksena integrand-funktio muutetaan muotoon rationaalinen toiminto muuttujasta $t$.

Esimerkki 1

Suorita integrointi:

\[\int \frac(x^(1/2) dx)(x^(3/4) +1) .\]

Ratkaisu:

$k=4$ on murto-osien $\frac(1)(2) ,\, \, \frac(3)(4) $ yhteinen nimittäjä.

\ \[\begin(array)(l) (\int \frac(x^(1/2) dx)(x^(3/4) +1) =4\int \frac(t^(2) ) (t^(3) +1) \cdot t^(3) dt =4\int \frac(t^(5) )(t^(3) +1) dt =4\int \left(t^( 2) -\frac(t^(2) )(t^(3) +1) \oikea)dt =4\int t^(2) dt -4\int \frac(t^(2) )(t ^(3) +1) dt =\frac(4)(3) \cdot t^(3) -) \\ (-\frac(4)(3) \cdot \ln |t^(3) +1 |+C)\end(array)\]

\[\int \frac(x^(1/2) dx)(x^(3/4) +1) =\frac(4)(3) \cdot \left+C\]

II

Kun etsitään integraali muotoa $\int R\left(x,\left(\frac(ax+b)(cx+d) \right)^(m/n) ,...,\left(\frac (ax+ b)(cx+d) \right)^(r/s) \right)dx $ on tarpeen suorittaa seuraava korvaus:

jossa $k$ on murto-osien $\frac(m)(n) ,...,\frac(r)(s) $ yhteinen nimittäjä.

Tämän substituution seurauksena integrandifunktio muunnetaan muuttujan $t$ rationaaliseksi funktioksi.

Esimerkki 2

Suorita integrointi:

\[\int \frac(\sqrt(x+4) )(x) dx .\]

Ratkaisu:

Tehdään seuraava vaihto:

\ \[\int \frac(\sqrt(x+4) )(x) dx =\int \frac(t^(2) )(t^(2) -4) dt =2\int \left(1 +\frac(4)(t^(2) -4) \oikea)dt =2\int dt +8\int \frac(dt)(t^(2) -4) =2t+2\ln \vasen |\frac(t-2)(t+2) \right|+C\]

Käänteisen vaihdon jälkeen saamme lopputuloksen:

\[\int \frac(\sqrt(x+4) )(x) dx =2\sqrt(x+4) +2\ln \left|\frac(\sqrt(x+4) -2)(\ sqrt(x+4) +2) \right|+C.\]

III

Kun löydetään integraali, jonka muoto on $\int R\left(x,\sqrt(ax^(2) +bx+c) \right)dx $, suoritetaan ns. Euler-substituutio (yksi kolmesta mahdollisesta substituutiosta on käytetty).

Eulerin ensimmäinen vaihto

Tapaukseen $a>

Ottamalla "+"-merkin $\sqrt(a) $:n edessä, saamme

Esimerkki 3

Suorita integrointi:

\[\int \frac(dx)(\sqrt(x^(2) +c) ) .\]

Ratkaisu:

Tehdään seuraava korvaus (tapaus $a=1>0$):

\[\sqrt(x^(2) +c) =-x+t,\, \, x=\frac(t^(2) -c)(2t) ,\, \, dx=\frac(t ^(2) +c)(2t^(2) ) dt,\, \, \sqrt(x^(2) +c) =-\frac(t^(2) -c)(2t) +t= \frac(t^(2) +c)(2t) .\] \[\int \frac(dx)(\sqrt(x^(2) +c) ) =\int \frac(\frac(t^) (2) +c)(2t^(2) ) dt)(\frac(t^(2) +c)(2t) ) =\int \frac(dt)(t) =\ln |t|+C \]

Käänteisen vaihdon jälkeen saamme lopputuloksen:

\[\int \frac(dx)(\sqrt(x^(2) +c) ) =\ln |\sqrt(x^(2) +c) +x|+C.\]

Eulerin toinen vaihto

Tapauksessa $c>0$ on suoritettava seuraava korvaus:

Ottamalla "+"-merkin $\sqrt(c) $:n edessä, saamme

Esimerkki 4

Suorita integrointi:

\[\int \frac((1-\sqrt(1+x+x^(2) ))^(2) )(x^(2) \sqrt(1+x+x^(2) ) ) dx .\]

Ratkaisu:

Tehdään seuraava vaihto:

\[\sqrt(1+x+x^(2) ) =xt+1.\]

\ \[\sqrt(1+x+x^(2) ) =xt+1=\frac(t^(2) -t+1)(1-t^(2) ) \] \

$\int \frac((1-\sqrt(1+x+x^(2) ))^(2) )(x^(2) \sqrt(1+x+x^(2) ) ) dx = \int \frac((-2t^(2) +t)^(2) (1-t)^(2) (1-t^(2))(2t^(2) -2t+2))( (1-t^(2))^(2) (2t-1)^(2) (t^(2) -t+1)(1-t^(2))^(2) ) dt =\ int \frac(t^(2) )(1-t^(2) ) dt =-2t+\ln \left|\frac(1+t)(1-t) \right|+C$ Tehtyään toisinpäin vaihto, saamme lopputuloksen:

\[\begin(array)(l) (\int \frac((1-\sqrt(1+x+x^(2) ))^(2) )(x^(2) \sqrt(1+x +x^(2) ) dx =-2\cdot \frac(\sqrt(1+x+x^(2) ) -1)(x) +\ln \left|\frac(x+\sqrt(1 + x+x^(2) ) -1)(x-\sqrt(1+x+x^(2) ) +1) \right|+C=-2\cdot \frac(\sqrt(1+x + x^(2) ) -1)(x) +) \\ (+\ln \left|2x+2\sqrt(1+x+x^(2) ) +1\right|+C) \end ( array)\]

Eulerin kolmas vaihto

Irrationaalisten funktioiden luokka on hyvin laaja, joten ei yksinkertaisesti voi olla universaalia tapaa integroida niitä. Tässä artikkelissa yritämme korostaa eniten tyypillisiä lajeja irrationaaliset integrandifunktiot ja yhdistä integrointimenetelmä niihin.

On tapauksia, joissa on tarkoituksenmukaista käyttää erotusmerkin merkitsemismenetelmää. Esimerkiksi kun etsitään muodon epämääräisiä integraaleja, missä s– rationaalinen murtoluku.

Esimerkki.

Etsi epämääräinen integraali .

Ratkaisu.

Sitä ei ole vaikea huomata. Siksi laitamme sen erotusmerkin alle ja käytämme antijohdannaisten taulukkoa:

Vastaus:

.

13. Murtoluku lineaarinen substituutio

Integraalit, joiden tyyppi on a, b, c, d ovat reaalilukuja, a, b,..., d, g luonnollisia lukuja, pelkistetään rationaalifunktion integraaleiksi substituutiolla, jossa K on funktion pienin yhteinen kerrannainen. murtolukujen nimittäjät

Korvaamisesta todellakin seuraa, että

eli x ja dx ilmaistaan ​​t:n rationaalisilla funktioilla. Lisäksi jokainen murto-osuuden aste ilmaistaan ​​t:n rationaalisen funktion kautta.

Esimerkki 33.4. Etsi integraali

Ratkaisu: Murtolukujen 2/3 ja 1/2 nimittäjien pienin yhteinen kerrannainen on 6.

Siksi laitamme x+2=t 6, x=t 6 -2, dx=6t 5 dt, joten

Esimerkki 33.5. Määritä korvaus integraalien löytämiseksi:

Ratkaisu: I 1 substituutiolle x=t 2, I 2 substituutiolle

14. Trigonometrinen substituutio

Tyypin integraalit pelkistetään funktioiden integraaleiksi, jotka rationaalisesti riippuvat trigonometrisista funktioista käyttämällä seuraavia trigonometrisiä substituutioita: x = ensimmäisen integraalin sint; x=a tgt toiselle integraalille;

Esimerkki 33.6. Etsi integraali

Ratkaisu: Laitetaan x=2 sin t, dx=2 cos tdt, t=arcsin x/2. Sitten

Tässä integrandi on rationaalinen funktio suhteessa x:ään ja Valitsemalla täydellinen neliö radikaalin alta ja tekemällä substituutio, osoitetun tyyppiset integraalit pelkistetään jo tarkasteltavan tyypin integraaleiksi, eli tyypin integraaleiksi. Nämä integraalit voidaan laskea käyttämällä sopivia trigonometrisiä substituutioita.

Esimerkki 33.7. Etsi integraali

Ratkaisu: Koska x 2 +2x-4=(x+1) 2 -5, niin x+1=t, x=t-1, dx=dt. Siksi Laitetaan

Huomautus: Integroitu tyyppi On tarkoituksenmukaista löytää käyttämällä substituutiota x=1/t.

15. Tarkka integraali

Olkoon funktio määritelty segmentissä ja oltava siinä antiderivaata. Ero on ns selvä integraali toimii segmentin varrella ja merkitsee. Niin,

Ero on siis kirjoitettu muotoon . Numeroita kutsutaan integraation rajoja .

Esimerkiksi yksi funktion antijohdannaisista. Siksi

16 . Jos c on vakioluku ja funktio ƒ(x) on integroitavissa , niin

eli vakiotekijä c voidaan ottaa pois määrätyn integraalin etumerkistä.

▼Määritetään integraalisumma funktiolle ƒ(x). Meillä on:

Tästä seuraa, että funktio c ƒ(x) on integroitavissa [a; b] ja kaava (38.1) on voimassa.▲

2. Jos funktiot ƒ 1 (x) ja ƒ 2 (x) ovat integroitavissa [a;b]:ssä, niin integroitavissa [a; b] niiden summa u

eli summan integraali on yhtä suuri kuin integraalien summa.

▼
▲

Ominaisuus 2 koskee minkä tahansa äärellisen määrän termejä.

3.

Tämä ominaisuus voidaan hyväksyä määritelmän mukaan. Tämän ominaisuuden vahvistaa myös Newton-Leibnizin kaava.

4. Jos funktio ƒ(x) on integroitavissa [a; b] ja a< с < b, то

eli koko segmentin integraali on yhtä suuri kuin tämän segmentin osien integraalien summa. Tätä ominaisuutta kutsutaan määrätyn integraalin additiivisuudeksi (tai additiivisuudeksi).

Jaettaessa janaa [a;b] osiin sisällytämme pisteen c jakopisteiden lukumäärään (tämä voidaan tehdä integraalisumman rajan riippumattomuuden vuoksi janan [a;b] jakomenetelmästä osiin). Jos c = x m, niin integraalisumma voidaan jakaa kahteen summaan:

Jokainen kirjoitetuista summista on integraali, vastaavasti, segmenteille [a; b], [a; s] ja [s; b]. Siirtymällä viimeisen yhtälön rajaan n → ∞ (λ → 0), saadaan yhtäläisyys (38.3).

Ominaisuus 4 pätee mihin tahansa pisteiden a, b, c sijaintiin (oletetaan, että funktio ƒ (x) on integroitavissa suuremmalla tuloksena olevista segmenteistä).

Joten esimerkiksi jos a< b < с, то

(käytettiin ominaisuuksia 4 ja 3).

5. "Keskiarvojen lause." Jos funktio ƒ(x) on jatkuva välillä [a; b], sitten on tonka, jossa on є [a; b] sellainen

▼Meillä on Newton-Leibnizin kaavalla

jossa F"(x) = ƒ(x). Sovellettaessa Lagrangen lausetta (funktion äärellisen inkrementin lause) erotukseen F(b)-F(a) saadaan

F(b)-F(a) = F"(c) (b-a) = ƒ(c) (b-a).▲

Ominaisuudella 5 ("keskiarvolause") arvolle ƒ (x) ≥ 0 on yksinkertainen geometrinen merkitys: määrätyn integraalin arvo on joillekin c є (a; b) yhtä suuri kuin suorakulmion pinta-ala korkeudella ƒ (c) ja pohjalla b-a (katso kuva 170). Määrä

kutsutaan funktion ƒ(x) keskiarvoksi välillä [a; b].

6. Jos funktio ƒ (x) säilyttää etumerkkinsä segmentissä [a; b], jossa a< b, то интегралимеет тот же знак, что и функция. Так, если ƒ(х)≥0 на отрезке [а; b], то

▼Keskiarvolauseella (ominaisuus 5)

missä c є [a; b]. Ja koska ƒ(x) ≥ 0 kaikille x О [a; b], sitten

ƒ(с)≥0, b-а>0.

Siksi ƒ(с) (b-а) ≥ 0, ts. ▲

7. Jatkuvien funktioiden välinen epäyhtälö välillä [a; b], (a

▼Koska ƒ 2 (x)-ƒ 1 (x) ≥0, sitten kun a< b, согласно свойству 6, имеем

Tai ominaisuuden 2 mukaan

Huomaa, että on mahdotonta erottaa eriarvoisuutta.

8. Integraalin estimointi. Jos m ja M ovat vastaavasti funktion y = ƒ (x) pienin ja suurin arvo segmentillä [a; b], (a< b), то

▼Koska minkä tahansa x є [a;b] kohdalla meillä on m≤ƒ(x)≤М, niin ominaisuuden 7 mukaan meillä on

Soveltamalla ominaisuutta 5 ääriintegraaleihin saadaan

▲

Jos ƒ(x)≥0, niin ominaisuus 8 on kuvattu geometrisesti: kaarevan puolisuunnikkaan pinta-ala on suljettu niiden suorakulmioiden alueiden väliin, joiden kanta on , ja joiden korkeus on m ja M (ks. kuva 171).

9. Määrätyn integraalin moduuli ei ylitä integrandin moduulin integraalia:

▼Soveltamalla ominaisuutta 7 ilmeisiin epäyhtälöihin -|ƒ(x)|≤ƒ(x)≤|ƒ(x)| saadaan

Siitä seuraa

▲

10. Määrätyn integraalin derivaatta suhteessa muuttujan ylärajaan on yhtä suuri kuin integrandi, jossa integrointimuuttuja korvataan tällä rajalla, ts.

Kuvion pinta-alan laskeminen on yksi vaikeimmista alueteorian ongelmista. Koulun geometrian kurssilla opimme löytämään geometristen perusmuotojen alueita, kuten ympyrän, kolmion, rombin jne. Kuitenkin paljon useammin joudut laskemaan monimutkaisempien lukujen alueita. Tällaisia ​​ongelmia ratkaistaessa on turvauduttava integraalilaskentaan.

Tässä artikkelissa tarkastelemme kaarevan puolisuunnikkaan pinta-alan laskemisen ongelmaa ja lähestymme sitä geometrisessa mielessä. Tämän avulla voimme selvittää suoran yhteyden määrätyn integraalin ja kaarevan puolisuunnikkaan alueen välillä.

Aiemmin löysimme sen derivaatan tietyn funktion perusteella, erilaisten kaavojen ja sääntöjen ohjaamana. Johdannaisella on lukuisia käyttötarkoituksia: se on liikkeen nopeus (tai yleisemmin minkä tahansa prosessin nopeus); funktion kuvaajan tangentin kulmakerroin; derivaatan avulla voit tutkia funktion monotonisuutta ja äärimmäisyyttä; se auttaa ratkaisemaan optimointiongelmia.

Mutta tunnetun liikelain mukaisen nopeuden löytämisongelman ohella on myös käänteinen ongelma - ongelma liikelain palauttamisesta tunnetun nopeuden mukaan. Tarkastellaanpa yhtä näistä ongelmista.

Esimerkki 1. Aineellinen piste liikkuu suoraviivaisesti, sen liikkeen nopeus hetkellä t saadaan kaavasta v=gt. Löydä liikkeen laki.
Ratkaisu. Olkoon s = s(t) haluttu liikelaki. Tiedetään, että s"(t) = v(t). Tämä tarkoittaa, että ongelman ratkaisemiseksi on valittava funktio s = s(t), jonka derivaatta on yhtä suuri kuin gt. Ei ole vaikea arvata että \(s(t) = \frac(gt^ 2)(2)\).
\(s"(t) = \left(\frac(gt^2)(2) \right)" = \frac(g)(2)(t^2)" = \frac(g)(2) \ cdot 2t = gt\)
Vastaus: \(s(t) = \frac(gt^2)(2) \)

Huomaa heti, että esimerkki on ratkaistu oikein, mutta epätäydellisesti. Saimme \(s(t) = \frac(gt^2)(2) \). Itse asiassa ongelmalla on äärettömän monta ratkaisua: mikä tahansa muotoa \(s(t) = \frac(gt^2)(2) + C\ oleva funktio, jossa C on mielivaltainen vakio, voi toimia laina liike, koska \(\left (\frac(gt^2)(2) +C \oikea)" = gt \)

Ongelman tarkentamiseksi jouduimme korjaamaan alkutilanteen: osoittamaan liikkuvan pisteen koordinaatin jossain vaiheessa, esimerkiksi t = 0. Jos esimerkiksi s(0) = s 0, niin yhtälö s(t) = (gt 2)/2 + C saadaan: s(0) = 0 + C, eli C = s 0. Nyt liikelaki on yksiselitteisesti määritelty: s(t) = (gt 2)/2 + s 0.

Matematiikassa toistensa käänteisoperaatioille annetaan eri nimiä, keksitään erityisiä merkintöjä, esimerkiksi: neliöinti (x 2) ja neliöjuuri (\(\sqrt(x)\)), sini (sin x) ja arcsini (arcsin x) ja jne. Tietyn funktion derivaatan löytämisprosessia kutsutaan erilaistuminen, ja käänteisoperaatio, eli prosessi, jossa funktio löydetään tietystä derivaatasta, on integraatio.

Itse termi "johdannainen" voidaan perustella "arkipäiväisillä termeillä": funktio y = f(x) "syntää" uuden funktion y" = f"(x). Funktio y = f(x) toimii ikään kuin se olisi "vanhempi", mutta matemaatikot eivät luonnollisesti kutsu sitä "vanhemmiksi" tai "tuottajaksi", he sanovat, että se on suhteessa funktioon y" = f"(x) , ensisijainen kuva tai primitiivinen.

Määritelmä. Funktiota y = F(x) kutsutaan antiderivaatiiviseksi funktiolle y = f(x) välissä X, jos yhtälö F"(x) = f(x) pätee \(x \in X\)

Käytännössä väliä X ei yleensä määritellä, vaan se on oletettu (funktion luonnollisena määrittelyalueena).

Annetaan esimerkkejä.
1) Funktio y = x 2 on antiderivaata funktiolle y = 2x, koska minkä tahansa x:n yhtälö (x 2)" = 2x on tosi
2) Funktio y = x 3 on antiderivaava funktiolle y = 3x 2, koska minkä tahansa x:n yhtälö (x 3)" = 3x 2 on tosi
3) Funktio y = sin(x) on antiderivaava funktiolle y = cos(x), koska minkä tahansa x:n yhtälö (sin(x))" = cos(x) on tosi

Löytäessäsi antijohdannaisia ​​ja johdannaisia ​​ei käytetä vain kaavoja, vaan myös joitain sääntöjä. Ne liittyvät suoraan vastaaviin johdannaisten laskentasääntöihin.

Tiedämme, että summan derivaatta on yhtä suuri kuin sen derivaattojen summa. Tämä sääntö luo vastaavan säännön antijohdannaisten löytämiseksi.

Sääntö 1. Summan antiderivaata on yhtä suuri kuin antiderivaattien summa.

Tiedämme, että vakiotekijä voidaan ottaa pois derivaatan merkistä. Tämä sääntö luo vastaavan säännön antijohdannaisten löytämiseksi.

Sääntö 2. Jos F(x) on f(x) antiderivaata, niin kF(x) on kf(x) antiderivaata.

Lause 1. Jos y = F(x) on antiderivaata funktiolle y = f(x), niin funktion y = f(kx + m) antiderivaata on funktio \(y=\frac(1)(k)F (kx+m) \)

Lause 2. Jos y = F(x) on antiderivaata funktiolle y = f(x) välillä X, niin funktiolla y = f(x) on äärettömän monta antiderivaavaa, ja ne kaikki ovat muotoa y = F(x) + C.

Integrointimenetelmät

Muuttuvan korvausmenetelmä (korvausmenetelmä)

Integrointimenetelmä substituutiolla sisältää uuden integrointimuuttujan (eli substituution) käyttöönoton. Tässä tapauksessa annettu integraali pelkistetään uudeksi integraaliksi, joka on taulukkomainen tai siihen pelkistävissä. Ei ole olemassa yleisiä menetelmiä korvausten valitsemiseksi. Kyky määrittää substituutio oikein hankitaan harjoittelemalla.
Olkoon tarpeen laskea integraali \(\textstyle \int F(x)dx \). Tehdään substituutio \(x= \varphi(t) \) missä \(\varphi(t) \) on funktio, jolla on jatkuva derivaatta.
Sitten \(dx = \varphi " (t) \cdot dt \) ja määrittelemättömän integraalin integrointikaavan invarianssiominaisuuden perusteella saadaan integrointikaava korvaamalla:
\(\int F(x) dx = \int F(\varphi(t)) \cdot \varphi " (t) dt \)

Muodon \(\textstyle \int \sin^n x \cos^m x dx \) lausekkeiden integrointi

Jos m on pariton, m > 0, niin substituutiosta on helpompi tehdä sin x = t.
Jos n on pariton, n > 0, niin on kätevämpää tehdä substituutio cos x = t.
Jos n ja m ovat parillisia, on kätevämpää tehdä substituutio tg x = t.

Integrointi osien mukaan

Integrointi osittain - soveltamalla seuraavaa integrointikaavaa:
\(\textstyle \int u \cdot dv = u \cdot v - \int v \cdot du \)
tai:
\(\textstyle \int u \cdot v" \cdot dx = u \cdot v - \int v \cdot u" \cdot dx \)

Joidenkin funktioiden epämääräisten integraalien (antiderivaatojen) taulukko

$$ \int 0 \cdot dx = C $$ $$ \int 1 \cdot dx = x+C $$ $$ \int x^n dx = \frac(x^(n+1))(n+1 ) +C \;\; (n \neq -1) $$ $$ \int \frac(1)(x) dx = \ln |x| +C $$ $$ \int e^x dx = e^x +C $$ $$ \int a^x dx = \frac(a^x)(\ln a) +C \;\; (a>0, \;\; a \neq 1) $$ $$ \int \cos x dx = \sin x +C $$ $$ \int \sin x dx = -\cos x +C $$ $ $ \int \frac(dx)(\cos^2 x) = \text(tg) x +C $$ $$ \int \frac(dx)(\sin^2 x) = -\text(ctg) x +C $$ $$ \int \frac(dx)(\sqrt(1-x^2)) = \text(arcsin) x +C $$ $$ \int \frac(dx)(1+x^2 ) = \teksti(arctg) x +C $$ $$ \int \teksti(ch) x dx = \teksti(sh) x +C $$ $$ \int \teksti(sh) x dx = \teksti(ch) ) x +C $$

Tässä osiossa käsitellään rationaalisten funktioiden integrointimenetelmää. 7.1. Lyhyt tietoa rationaalisista funktioista Yksinkertaisin rationaalinen funktio on kymmenesosasteen polynomi, ts. funktio muotoa jossa ovat reaalivakiot, ja a0 Φ 0. Polynomi Qn(x), jonka kerrointa a0 = 1 kutsutaan pelkistetyksi. Reaalilukua b kutsutaan polynomin Qn(z) juureksi, jos Q„(b) = 0. Tiedetään, että jokainen polynomi Qn(x), jolla on todelliset kertoimet, hajotetaan yksiselitteisesti reaalitekijöiksi, joiden muoto on p, q ovat todellisia kertoimia, ja neliötekijöillä ei ole todellisia juuria, joten niitä ei voida hajottaa todellisiksi lineaarisiksi tekijöiksi. Yhdistämällä identtiset tekijät (jos niitä on) ja olettamalla yksinkertaisuuden vuoksi, että polynomi Qn(x) pelkistyy, voimme kirjoittaa sen tekijöiden jakamisen muodossa jossa ovat luonnolliset luvut. Koska polynomin Qn(x) aste on yhtä suuri kuin n, niin kaikkien eksponentien a, /3,..., A summa, joka on lisätty kaikkien eksponentien ω,..., q kaksoissummalla, on yhtä suuri. to n: Polynomin juurta a kutsutaan yksinkertaiseksi tai yksinkertaiseksi , jos a = 1, ja moninkertaiseksi, jos a > 1; Lukua a kutsutaan juuren a monikertaiseksi. Sama koskee muita polynomin juuria. Rationaalinen funktio f(x) tai rationaalinen murtoluku on kahden polynomin suhde, ja oletetaan, että polynomeilla Pm(x) ja Qn(x) ei ole yhteisiä kertoimia. Rationaalista murtolukua kutsutaan oikeaksi, jos osoittajan polynomin aste on pienempi kuin nimittäjässä olevan polynomin aste, ts. Jos m n, niin rationaalista murtolukua kutsutaan vääräksi murtoluvuksi, ja tässä tapauksessa jakamalla osoittaja nimittäjällä polynomien jakosäännön mukaisesti, se voidaan esittää muodossa, jossa on joitain polynomeja, ja ^^ on oikea rationaalinen murto-osa. Esimerkki 1. Rationaalinen murtoluku on väärä murtoluku. Jakamalla "kulmalla", meillä on Siksi. Tässä. ja se on oikea murto-osa. Näiden vakioiden löytämiseksi yhtälön (I) oikea puoli tuodaan yhteiseen nimittäjään, ja sitten vasemman ja oikean puolen osoittajien kertoimet samalla potenssilla tasataan. Tämä antaa lineaarisen yhtälöjärjestelmän, josta löydetään tarvittavat vakiot. . Tätä tuntemattomien vakioiden löytämismenetelmää kutsutaan määrittelemättömien kertoimien menetelmäksi. Joskus on kätevämpää käyttää toista menetelmää tuntemattomien vakioiden etsimiseen, mikä koostuu siitä, että osoittajien yhtälön jälkeen saadaan identiteetti x:n suhteen, jossa argumentille x annetaan joitain arvoja, esim. juurista, mikä johtaa yhtälöihin vakioiden löytämiseksi. On erityisen kätevää, jos nimittäjällä Q„(x) on vain todellisia yksinkertaisia ​​juuria. Esimerkki 2. Jaa rationaalinen murto yksinkertaisemmiksi murto-osiksi. Jaamme nimittäjän kertoimiin: Koska nimittäjän juuret ovat todellisia ja erilaisia, niin kaavan (1) perusteella murto-osan hajoaminen yksinkertaisimpaan on muotoa: Vähentämällä "sen tasa-arvon oikea kunnia" yhteinen nimittäjä ja yhtälöimällä sen vasemmalla ja oikealla puolella olevat osoittajat, saadaan identiteetti tai Löydämme tuntemattomat kertoimet A. 2?, C kahdella tavalla. Ensimmäinen tapa Tasaa kertoimet samoille x:n, t.v:n potenssille. (vapaalla termillä) ja identiteetin vasemmalla ja oikealla puolella saadaan lineaarinen yhtälöjärjestelmä tuntemattomien kertoimien A, B, C löytämiseksi: Tällä järjestelmällä on ainutlaatuinen ratkaisu C Toinen menetelmä. Koska nimittäjän juuret repeytyvät kohdassa i 0, saadaan 2 = 2A, josta A * 1; g i 1, saamme -1 * -B, josta 5 * 1; x i 2, saamme 2 = 2C. mistä C» 1, ja vaadittu laajennus on muotoa 3. Rehlozhnt ei yksinkertaisin murtoluku rationaalinen murtoluku 4 Jaamme polynomin, joka on päinvastainen, tekijöiksi: . Nimittäjällä on kaksi erilaista reaalijuurta: x\ = 0 monikerroin 3. Siksi tämän murtoluvun hajottaminen ei ole yksinkertaisin: Pelistämällä oikean puolen yhteiseksi nimittäjäksi löydämme tai Ensimmäinen menetelmä. Kertoimien yhtäläisyys samoille x:n potenssille viimeisen identiteetin vasemmalla ja oikealla puolella. saamme lineaarisen yhtälöjärjestelmän. Tällä järjestelmällä on ainutlaatuinen ratkaisu ja vaadittava laajennus on toinen menetelmä. Tuloksena olevassa identiteetissä, kun x = 0, saadaan 1 a A2 tai A2 = 1; kenttä* homo x = -1, saamme -3 i B) tai Bj i -3. Kun korvataan kertoimien A\ ja B) löydetyt arvot, identiteetti saa muotoa tai Putting x = 0 ja sitten x = -I. huomaamme, että = 0, B2 = 0 ja. tämä tarkoittaa B\ = 0. Näin saadaan jälleen esimerkki 4. Laajenna rationaalinen murto-osa 4 yksinkertaisemmiksi murto-osiksi. Siksi yksinkertaisiin murtolukuihin hajotuksen tulisi olla muodossa Täältä saamme tai. Yhtälöimällä x:n synaksipotenssien kertoimet viimeisen yhtälön vasemmalla ja oikealla puolella, saamme mistä löydämme, ja siksi on huomattava, että joissakin tapauksissa laajennuksia yksinkertaisiin murtolukuihin voidaan saada nopeammin ja helpommin toimimalla jollain muulla tavalla, käyttämättä määräämättömien kertoimien menetelmää Esimerkiksi saadaksesi murto-osan jaottelun esimerkissä 3, voit lisätä ja vähentää osoittajassa 3x2 ja jakaa alla olevan kuvan mukaisesti. 7.2. Yksinkertaisten murtolukujen integrointi, Kuten edellä mainittiin, mikä tahansa väärä rationaalinen murtoluku voidaan esittää jonkin polynomin ja oikean rationaalisen murtoluvun summana (§7), ja tämä esitys on ainutlaatuinen. Polynomin integrointi ei ole vaikeaa, joten harkitse oikean rationaalisen murtoluvun integrointia. Koska mikä tahansa oikea rationaalinen murtoluku voidaan esittää yksinkertaisten murtolukujen summana, sen integrointi pelkistyy yksinkertaisten murtolukujen integraatioon. Tarkastellaanpa nyt kysymystä heidän integroinnistaan. III. Kolmannen tyypin yksinkertaisimman murtoluvun integraalin löytämiseksi eristetään binomiaalin täydellinen neliö neliötrinomista: Koska toinen termi on yhtä suuri kuin a2, missä ja sitten teemme substituution. Sitten, ottaen huomioon integraalin lineaariset ominaisuudet, saadaan: Esimerkki 5. Etsi integraali 4 Integrandifunktio on kolmannen tyypin yksinkertaisin murto-osa, koska neliötrinomilla x1 + Ax + 6 ei ole todellisia juuria (sen diskriminantilla on negatiivinen: , ja osoittaja sisältää ensimmäisen asteen polynomin. Siksi toimimme seuraavasti: 1) valitse täydellinen neliö nimittäjästä 2) korvaa (tässä 3) * yhdellä integraalilla Löytääksesi integraalin. Neljännen tyypin yksinkertaisin murto-osa, laitamme, kuten edellä, . Sitten saadaan A:lla merkitty oikealla puolella oleva integraali ja muunnetaan se seuraavasti: Oikean puolen integraali integroidaan osilla, olettaen mistä tai Rationaalisten funktioiden integrointi Lyhyt tietoa rationaalisista funktioista Yksinkertaisten murtolukujen integrointi Yleinen tapaus Irrationaalin integrointi funktiot Eulerin ensimmäinen substituutio Toinen Euler-substituutio Kolmas substituutio Euler Olemme saaneet ns. toistuvan kaavan, jonka avulla voimme löytää integraalin Jk mille tahansa k = 2, 3,. ... Todellakin, integraali J\ on taulukkomuotoinen: Laittamalla toistuvuuskaavaan, löydämme tietäen ja laittamalla A = 3, voimme helposti löytää Jj ja niin edelleen. Lopputuloksena korvaamalla kaikkialla t:n ja a:n sijaan niiden lausekkeet x:n ja kertoimien p ja q suhteen, saadaan alkuperäiselle integraalille sen lauseke x:n ja annetuilla luvuilla M, LG, p, q. Esimerkki 8. Uusi integraali ”Integrandifunktio on neljännen tyypin yksinkertaisin murto-osa, koska neliötrinomin diskriminantti on negatiivinen, ts. Tämä tarkoittaa, että nimittäjällä ei ole todellisia juuria ja osoittaja on 1. asteen polynomi. 1) Valitsemme nimittäjästä kokonaisen neliön 2) Teemme korvauksen: Integraali saa muotoa: Laitetaan toistuvuuskaava * = 2, a3 = 1. meillä on, ja siksi haluttu integraali on yhtä suuri Palattaessa muuttujaan x saadaan lopulta 7.3. Yleinen tapaus Kappaleiden tuloksista. Tämän osan 1 ja 2 seuraavat välittömästi tärkeää lausetta. Lause! 4. Minkä tahansa rationaalisen funktion epämääräinen integraali on aina olemassa (väleillä, joissa murto-osan nimittäjä Q„(x) φ 0) ja se ilmaistaan ​​äärellisen määrän alkeisfunktioiden kautta, eli se on algebrallinen summa, termit joista voidaan kertoa vain rationaalisia murtolukuja, luonnollisia logaritmeja ja arktangentteja. Joten murto-rationaalisen funktion epämääräisen integraalin löytämiseksi tulee edetä seuraavalla tavalla: 1) jos rationaalinen murtoluku on virheellinen, niin jakamalla osoittaja nimittäjällä, koko osa eristetään, eli tämä funktio. on esitetty polynomin ja oikean rationaalisen murtoluvun summana; 2) sitten tuloksena olevan oikean murtoluvun nimittäjä hajotetaan lineaaristen ja neliötekijöiden tuloksi; 3) tämä oikea murto-osa jaetaan yksinkertaisten murto-osien summaksi; 4) integraalin lineaarisuutta ja vaiheen 2 kaavoja käyttämällä löydetään kunkin termin integraalit erikseen. Esimerkki 7. Etsi integraali M Koska nimittäjä on kolmannen kertaluvun polynomi, integrandifunktio on virheellinen murto-osa. Korostamme sen koko osan: Siksi meillä on. Oikean murtoluvun nimittäjällä on phi erilliset todelliset juuret: ja siksi sen hajoamisella yksinkertaisiksi murtoluvuiksi on muoto, josta löydämme. Antamalla argumentille x arvot, jotka ovat yhtä suuria kuin nimittäjän juuret, saamme tästä identiteetistä, että: Siksi vaadittu integraali on yhtä suuri kuin esimerkki 8. Etsi integraali 4 Integrandi on oikea murtoluku, jonka nimittäjä on kaksi erilaista reaalijuurta: x - 1:n O-kerroin ja 3:n kerrannaiskerroin x = 1, Siksi integrandin laajentaminen yksinkertaisiksi murtoluvuiksi saa muotoa Tuo tämän yhtälön oikean puolen yhteiseen nimittäjään ja pienentää yhtälön molempia puolia tällä nimittäjällä saamme tai. Yhdistämme kertoimet samalle x:n potenssille tämän identiteetin vasemmalla ja oikealla puolella: Täältä löydämme. Korvaamalla kerrointen löydetyt arvot laajennuksen saamme Integroimalla: Esimerkki 9. Etsi integraali 4 Murtoluvun nimittäjällä ei ole todellisia juuria. Siksi integrandin laajennuksen yksinkertaisiksi murtoluvuiksi saamme tämän identiteetin vasemmalla ja oikealla puolella olevien x:n samojen potenssien kertoimien muotoa siten, mistä löydämme, ja siksi huomautuksen. Esitetyssä esimerkissä integrandifunktio voidaan esittää yksinkertaisten murtolukujen summana yksinkertaisemmalla tavalla, nimittäin murtoluvun osoittajassa valitaan nimittäjästä bin ja sitten tehdään termi jako: § 8. Irrationaalisten funktioiden integrointi Funktion muotoa, jossa Pm ja £?„ ovat astetyyppisiä polynomeja, muuttujissa uub2,... kutsutaan ubu2j:n rationaalifunktioksi... Esimerkiksi toisen asteen polynomiksi kahdessa muuttujassa u\ ja u2 on muoto, jossa - joitain reaalivakioita, ja esimerkki 1, funktio on muuttujien z ja y rationaalinen funktio, koska se edustaa sekä kolmannen asteen polynomin että polynomin suhdetta viidennen asteen eikä se ole marjakuusifunktio. Siinä tapauksessa, että muuttujat puolestaan ​​ovat muuttujan x funktioita: silloin funktiota ] kutsutaan esimerkin funktioiden rationaaliseksi funktioksi. Funktio on r- ja rvdikvlv Pryaivr 3:n rationaalinen funktio. Muodon funktio ei ole x:n ja radikaalin y/r1 + 1 rationaalinen funktio, vaan se on funktioiden rationaalinen funktio. Kuten esimerkit osoittavat, irrationaalin integraalit funktioita ei aina ilmaista perusfunktioiden kautta. Esimerkiksi sovelluksissa usein esiintyviä integraaleja ei ilmaista perusfunktioina; näitä integraaleja kutsutaan ensimmäisen ja toisen tyyppisiksi elliptisiksi integraaleiksi. Tarkastellaanpa niitä tapauksia, joissa irrationaalisten funktioiden integraatio voidaan pelkistää joidenkin substituutioiden avulla rationaalisten funktioiden integraatioksi. 1. Olkoon tarpeen löytää integraali, jossa R(x, y) on sen argumenttien x ja y rationaalinen funktio; m £ 2 - luonnollinen luku; a, 6, c, d ovat todellisia vakioita, jotka täyttävät ehdon ad - bc ^ O (jos ad - be = 0, kertoimet a ja b ovat verrannollisia kertoimiin c ja d, joten suhde ei riipu x:stä tämä tarkoittaa, että tässä tapauksessa integrandifunktio on muuttujan x rationaalinen funktio, jonka integroinnista keskusteltiin aiemmin). Seuraavaksi löydämme tai yksinkertaistamisen jälkeen Siksi missä A1 (t) on *:n rationaalinen funktio, koska rationaalisen funktion rationaaliset funadiat sekä rationaalisten funktioiden tulo ovat rationaalifunktioita. Osaamme integroida rationaalisia toimintoja. Olkoon sitten vaadittu integraali yhtä suuri kuin At. IvYti integraali 4 Integrand*-funktio on rationaalinen funktio. Siksi asetetaan t = Siis Rationaalisten funktioiden integrointi Lyhyt tietoa rationaalisista funktioista Yksinkertaisten murtolukujen integrointi Yleinen tapaus Irrationaalisten funktioiden integrointi Eulerin ensimmäinen substituutio Eulerin toinen substituutio Eulerin kolmas substituutio Näin saadaan Primar 5. Etsi integraali Murtoluvun yhteinen nimittäjä potenssien x eksponentti on 12, joten integrandi funktio voidaan esittää muodossa 1 _ 1_, mikä osoittaa, että se on rationaalinen funktio: Otetaan tämä huomioon. Näin ollen 2. Tarkastellaan muotoisia inteph-funktioita, joissa osaintefaalinen funktio on sellainen, että korvaamalla siinä oleva radikaali \/ax2 + bx + c y:llä, saadaan funktio R(x) y) - rationaalinen molempien argumenttien x suhteen. ja y. Tämä integraali pelkistetään toisen muuttujan rationaalisen funktion integraaliksi käyttämällä Eulerin substituutioita. 8.1. Eulerin ensimmäinen substituutio Olkoon kerroin a > 0. Asetetaan tai Siten löydetään x u:n rationaalisena funktiona, mikä tarkoittaa, että esitetty substituutio ilmaisee siis rationaalisesti *:lla. Siksi meillä on huomautus. Ensimmäinen Euler-substituutio voidaan ottaa myös muodossa Esimerkki 6. Etsitään integraali Siksi meillä on dx Eulerin substituutio, osoita, että Y 8.2. Eulerin toinen substituutio Olkoon trinomilla ax2 + bx + c eri reaalijuuret R] ja x2 (kertoimella voi olla mikä tahansa etumerkki). Tässä tapauksessa oletetaan Koska siitä lähtien saamme Koska x,dxn y/ax2 + be + c ilmaistaan ​​rationaalisesti t:llä, niin alkuperäinen integraali pelkistetään rationaalisen funktion integraaliksi, eli missä Tehtävä. Osoita Eulerin ensimmäistä substituutiota käyttämällä, että se on t:n rationaalinen funktio. Esimerkki 7. Etsi integraali dx M -funktio ] - x1:llä on erilaiset todelliset juuret. Tästä syystä käytämme toista Euler-substituutiota korvaamalla löydetyt lausekkeet Given?v*gyvl; saamme 8.3. Kolmas Euler substascom Olkoon kerroin c > 0. Muutetaan muuttuja asettamalla. Huomaa, että rationaalisen funktion integraalin pelkistämiseksi integraaliksi riittää ensimmäinen ja toinen Euler-substituutio. Itse asiassa, jos diskriminantti b2 -4ac > 0, niin toisen asteen trinomin ax + bx + c juuret ovat reaalisia, ja tässä tapauksessa voidaan soveltaa toista Eulerin substituutiota. Jos sitten trinomin etumerkki ax2 + bx + c osuu yhteen kertoimen a etumerkin kanssa ja koska trinomin on oltava positiivinen, niin a > 0. Tässä tapauksessa voidaan soveltaa Eulerin ensimmäistä substituutiota. Yllä mainitun tyyppisten integraalien löytämiseksi ei aina ole suositeltavaa käyttää Eulerin substituutioita, koska niille on mahdollista löytää muita integrointimenetelmiä, jotka johtavat tavoitteeseen nopeammin. Tarkastellaan joitain näistä integraaleista. 1. Löytääksesi muodon integraalit, eristä oikea neliö kolmiosaisen neliöstä: missä Tämän jälkeen tee substituutio ja saa missä kertoimilla a ja P on eri etumerkit tai ne ovat molemmat positiivisia. Sillä, ja myös arvolla > 0, integraali pelkistetään logaritmiksi, ja jos on, arsiniseksi. klo. Etsi imtegral 4 Sokak sitten. Olettaen, että saamme Prmmar 9. Etsi. Olettaen x -, meillä on 2. Muodon integraali pelkistetään integraaliksi y vaiheesta 1 seuraavasti. Ottaen huomioon, että derivaatta ()" = 2, korostamme sen osoittajassa: 4 Tunnistamme osoittajassa radikaalilausekkeen derivaatan. Koska (x, niin meillä on esimerkin 9 tulos huomioon ottaen 3. Integraalit, joiden muoto on P„(x) on polynomin n-aste, voidaan löytää epämääräisten kertoimien menetelmällä, joka koostuu seuraavasta. Oletetaan, että yhtälö on Esimerkki 10. Mahtava integraali missä Qn-i (s) on (n - 1) asteen polynomi, jolla on epämääräisiä kertoimia: Tuntemattomien kertoimien löytämiseksi erotetaan (1):n oikea puoli yhteiseksi nimittäjäksi. vasemman puolen nimittäjä, eli y/ax2 + bx + c, vähentäen (2):n molemmat puolet, joilla saadaan identiteetti, jonka molemmilla puolilla on n-asteisia polynomeja (3) vasemmalle ja oikealle puolelle saadaan n + 1 yhtälöt, joista saadaan tarvittavat kertoimet j4*(fc = 0,1,2,..., n ) korvaamalla niiden arvot oikealle puolelle (1) ja löytämällä integraalin + c saamme vastauksen tälle integraalille. Esimerkki 11. Etsi integraali Laitetaan Erottamalla yhtälön molemmat puvut, saadaan Tuomalla oikea puoli yhteiseen nimittäjään ja vähentämällä molemmat puolet sillä, saadaan identiteetti tai. Yhtälöimällä kertoimet samoilla x:n potenssilla saadaan yhtälöjärjestelmä, josta löydämme = Sitten löydämme integraalin yhtälön (4) oikealta puolelta: Näin ollen vaadittava integraali on yhtä suuri

Ei ole olemassa universaalia tapaa ratkaista irrationaalisia yhtälöitä, koska niiden luokka vaihtelee määrällisesti. Artikkelissa tuodaan esiin tyypillisiä yhtälötyyppejä substituutiolla integrointimenetelmällä.

Suoran integrointimenetelmän käyttämiseksi on tarpeen laskea ∫ k x + b p d x -tyyppiset epämääräiset integraalit, joissa p on rationaalinen murtoluku, k ja b reaalikertoimia.

Esimerkki 1

Etsi ja laske funktion y = 1 3 x - 1 3 antiderivaatat.

Ratkaisu

Integrointisäännön mukaan on tarpeen soveltaa kaavaa ∫ f (k x + b) d x = 1 k F (k x + b) + C, ja antiderivaatataulukko osoittaa, että tähän funktioon on olemassa valmis ratkaisu . Me ymmärrämme sen

∫ d x 3 x - 1 3 = ∫ (3 x - 1) - 1 3 d x = 1 3 1 - 1 3 + 1 (3 x - 1) - 1 3 + 1 + C = = 1 2 (3 x - 1 ) 2 3 + C

Vastaus:∫ d x 3 x - 1 3 = 1 2 (3 x - 1) 2 3 + C .

On tapauksia, joissa on mahdollista käyttää differentiaalimerkin yhdistämismenetelmää. Tämä ratkaistaan ​​periaatteella löytää epämääräiset integraalit muotoa ∫ f " (x) · (f (x)) p d x , kun p:n arvoa pidetään rationaalisena murtolukuna.

Esimerkki 2

Etsi epämääräinen integraali ∫ 3 x 2 + 5 x 3 + 5 x - 7 7 6 d x .

Ratkaisu

Huomaa, että d x 3 + 5 x - 7 = x 3 + 5 x - 7 "d x = (3 x 2 + 5) d x. Sitten on tarpeen sisällyttää differentiaalimerkki käyttämällä antiderivaatataulukoita. Saamme, että

∫ 3 x 2 + 5 x 3 + 5 x - 7 7 6 d x = ∫ (x 3 + 5 x - 7) - 7 6 (3 x 2 + 5) d x = = ∫ (x 3 + 5 x - 7 ) - 7 6 p (x 3 + 5 x - 7) = x 3 + 5 x - 7 = z = = ∫ z - 7 6 d z = 1 - 7 6 + 1 z - 7 6 + 1 + C = - 6 z - 1 6 + C = z = x 3 + 5 x - 7 = - 6 (x 3 + 5 x - 7) 6 + C

Vastaus:∫ 3 x 2 + 5 x 3 + 5 x - 7 7 6 d x = - 6 (x 3 + 5 x - 7) 6 + C .

Epämääräisten integraalien ratkaisemiseen liittyy muotoa ∫ d x x 2 + p x + q oleva kaava, jossa p ja q ovat reaalikertoimia. Sitten sinun on valittava koko neliö juuren alta. Me ymmärrämme sen

x 2 + p x + q = x 2 + p x + p 2 2 - p 2 2 + q = x + p 2 2 + 4 q - p 2 4

Käyttämällä epämääräisten integraalien taulukossa olevaa kaavaa saamme:

∫ d x x 2 ± α = ln x + x 2 ± α + C

Sitten lasketaan integraali:

∫ d x x 2 + p x + q = ∫ d x x + p 2 2 + 4 q - p 2 4 = = ln x + p 2 + x + p 2 2 + 4 q - p 2 4 + C = = ln x + p 2 + x 2 + p x + q + C

Esimerkki 3

Etsi muodon ∫ d x 2 x 2 + 3 x - 1 epämääräinen integraali.

Ratkaisu

Laskeaksesi sinun on poistettava numero 2 ja asetettava se radikaalin eteen:

∫ d x 2 x 2 + 3 x - 1 = ∫ d x 2 x 2 + 3 2 x - 1 2 = 1 2 ∫ d x x 2 + 3 2 x - 1 2

Valitse täydellinen neliö radikaalilausekkeessa. Me ymmärrämme sen

x 2 + 3 2 x - 1 2 = x 2 + 3 2 x + 3 4 2 - 3 4 2 - 1 2 = x + 3 4 2 - 17 16

Sitten saadaan epämääräinen integraali muotoa 1 2 ∫ d x x 2 + 3 2 x - 1 2 = 1 2 ∫ d x x + 3 4 2 - 17 16 = = 1 2 ln x + 3 4 + x 2 + 3 2 x - 12 + C

Vastaus: d x x 2 + 3 x - 1 = 1 2 ln x + 3 4 + x 2 + 3 2 x - 1 2 + C

Irrationaalisten funktioiden integrointi suoritetaan samalla tavalla. Koskee muotoa y = 1 - x 2 + p x + q olevia funktioita.

Esimerkki 4

Etsi epämääräinen integraali ∫ d x - x 2 + 4 x + 5 .

Ratkaisu

Ensin sinun on johdettava lausekkeen nimittäjän neliö juuren alta.

∫ d x - x 2 + 4 x + 5 = ∫ d x - x 2 - 4 x - 5 = = ∫ d x - x 2 - 4 x + 4 - 4 - 5 = ∫ d x - x - 2 2 - 9 = ∫ d x - (x - 2) 2 + 9

Taulukon integraalin muoto on ∫ d x a 2 - x 2 = a r c sin x a + C, jolloin saadaan, että ∫ d x - x 2 + 4 x + 5 = ∫ d x - (x - 2) 2 + 9 = a r c sin x - 2 3 +C

Vastaus:∫ d x - x 2 + 4 x + 5 = a r c sin x - 2 3 + C .

Prosessi, jolla löydetään muotoa y = M x + N x 2 + p x + q olevat antiderivatiiviset irrationaaliset funktiot, joissa olemassa olevat M, N, p, q ovat todellisia kertoimia ja ovat samanlaisia ​​kuin kolmannen tyypin yksinkertaisten murtolukujen integrointi . Tässä muutoksessa on useita vaiheita:

summaamalla differentiaali juuren alle, eristämällä lausekkeen koko neliö juuren alta käyttämällä taulukkokaavoja.

Esimerkki 5

Etsi funktion y = x + 2 x 2 - 3 x + 1 antiderivaatat.

Ratkaisu

Ehdosta saamme, että d (x 2 - 3 x + 1) = (2 x - 3) d x ja x + 2 = 1 2 (2 x - 3) + 7 2, sitten (x + 2) d x = 1 2 (2 x - 3) + 7 2 d x = 1 2 d (x 2 - 3 x + 1) + 7 2 d x .

Lasketaan integraali: ∫ x + 2 x 2 - 3 x + 1 d x = 1 2 ∫ d (x 2 - 3 x + 1) x 2 - 3 x + 1 + 7 2 ∫ d x x 2 - 3 x + 1 = = 1 2 ∫ (x 2 - 3 x + 1) - 1 2 d (x 2 - 3 x + 1) + 7 2 ∫ d x x - 3 2 2 - 5 4 = = 1 2 1 - 1 2 + 1 x 2 - 3 x + 1 - 1 2 + 1 + 7 2 ln x - 3 2 + x - 3 2 - 5 4 + C = = x 2 - 3 x + 1 + 7 2 ln x - 3 2 + x 2 - 3 x + 1 + C

Vastaus:∫ x + 2 x 2 - 3 x + 1 d x = x 2 - 3 x + 1 + 7 2 ln x - 3 2 + x 2 - 3 x + 1 + C .

Funktion ∫ x m (a + b x n) p d x epämääräisten integraalien haku suoritetaan korvausmenetelmällä.

Ratkaisua varten on otettava käyttöön uusia muuttujia:

1. Kun p on kokonaisluku, x = z N otetaan huomioon ja N on m:n yhteinen nimittäjä, n.
2. Kun m + 1 n on kokonaisluku, niin a + b x n = z N ja N on p:n nimittäjä.
3. Kun m + 1 n + p on kokonaisluku, vaaditaan muuttuja a x - n + b = z N, ja N on luvun p nimittäjä.

Esimerkki 6

Etsi määrällinen integraali ∫ 1 x 2 x - 9 d x .

Ratkaisu

Saamme, että ∫ 1 x 2 x - 9 d x = ∫ x - 1 · (- 9 + 2 x 1) - 1 2 d x . Tästä seuraa, että m = - 1, n = 1, p = - 1 2, jolloin m + 1 n = - 1 + 1 1 = 0 on kokonaisluku. Voit ottaa käyttöön uuden muuttujan muodossa - 9 + 2 x = z 2. On välttämätöntä ilmaista x z:llä. Tuotoksena saamme sen

9 + 2 x = z 2 ⇒ x = z 2 + 9 2 ⇒ d x = z 2 + 9 2 " d z = z d z - 9 + 2 x = z

On välttämätöntä tehdä korvaus annettuun integraaliin. Meillä se on

∫ d x x 2 x - 9 = ∫ d z z 2 + 9 2 z = 2 ∫ d z z 2 + 9 = = 2 3 a r c t g z 3 + C = 2 3 a r c c t g 2 x - 9 3 + C

Vastaus:∫ d x x 2 x - 9 = 2 3 a r c c t g 2 x - 9 3 + C .

Irrationaalisten yhtälöiden ratkaisun yksinkertaistamiseksi käytetään perusintegrointimenetelmiä.

Jos huomaat tekstissä virheen, korosta se ja paina Ctrl+Enter