3. loeng. Simplex tabelid. Algoritm simpleks meetod.

§ 3 LIHTNE MEETOD

3.1. Simpleksmeetodi üldine idee. Geomeetriline tõlgendus

Graafiline meetod on rakendatav väga kitsale probleemide klassile lineaarne programmeerimine: see suudab tõhusalt lahendada probleeme, mis ei sisalda rohkem kui kahte muutujat. Käsitleti lineaarse programmeerimise põhiteoreeme, millest järeldub, et kui lineaarse programmeerimise ülesandel on optimaalne lahendus, siis vastab see lahenduspolühedri vähemalt ühele nurgapunktile ja langeb kokku, vastavalt vähemalt, piirangute süsteemi ühe lubatava põhilahendusega. Näidati iga lineaarse programmeerimise probleemi lahendamise viis: loetleda piiratud arv piirangute süsteemi teostatavaid põhilahendusi ja valida nende hulgast see, millel sihtfunktsioon teeb optimaalse lahenduse. Geomeetriliselt vastab see lahenduse hulktahuka kõigi nurgapunktide loetlemisele. Selline ammendav otsing viib lõpuks optimaalse lahenduseni (kui see on olemas), kuid selle praktiline rakendamine on seotud tohutute raskustega, kuna tegelike probleemide puhul võib teostatavate põhilahenduste arv, kuigi piiratud, olla äärmiselt suur.

Otsitavate lubatavate põhilahenduste arvu saab vähendada, kui otsingut ei teostata juhuslikult, vaid võttes arvesse lineaarfunktsiooni muutusi, s.o. tagades, et kõik järgmine lahendus oli lineaarfunktsiooni väärtuste järgi eelmisest "parem" (või vähemalt "mitte halvem") (maksimumi leidmisel suurendades, miinimumi leidmisel vähendades
). See otsing võimaldab teil optimaalse leidmisel sammude arvu vähendada. Selgitame seda graafilise näitega.

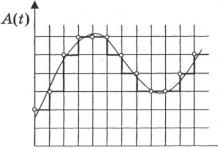
Olgu teostatavate lahenduste piirkond esindatud hulknurgaga ABCDE. Oletame, et selle nurgapunkt A vastab esialgsele teostatavale baaslahendusele. Juhuslik otsing eeldaks viie teostatava baaslahenduse testimist, mis vastavad polügooni viiele nurgapunktile. Jooniselt on aga selgelt näha, et peale tipu A kasulik on liikuda naabertippu IN, ja seejärel optimaalsesse punkti KOOS. Viie tipu asemel läbisime ainult kolm tippu, parandades järjekindlalt lineaarfunktsiooni.

Lahenduse järjestikuse täiustamise idee pani aluse universaalsele meetodile lineaarse programmeerimise probleemide lahendamiseks - simpleksmeetod või plaani järjestikuse täiustamise meetod.

Simpleksmeetodi geomeetriline tähendus seisneb järjestikuses üleminekus piirangu polüeedri ühest tipust (nimetatakse esialgseks) naaberpunktile, milles lineaarne funktsioon võtab ülesande eesmärgi suhtes parima (vähemalt mitte halvima) väärtuse; kuni optimaalse lahenduse leidmiseni - tipp kus optimaalne väärtus eesmärgi funktsioon (kui probleemil on lõplik optimum).

Simpleksmeetodi pakkus esmakordselt välja Ameerika teadlane J. Danzig 1949. aastal, kuid juba 1939. aastal töötas meetodi ideed välja vene teadlane L.V. Kantorovitš.

Simpleksmeetod, mis võimaldab lahendada mis tahes lineaarse programmeerimise probleemi, on universaalne. Praegu kasutatakse seda arvutiarvutustes, kuid lihtsaid näiteid simpleksmeetodil saab lahendada käsitsi.

Simpleksmeetodi - lahenduse järjestikuse täiustamise - rakendamiseks on vaja valdada kolm põhielementi:

meetod probleemi esialgse võimaliku põhilahenduse määramiseks;

parimale (täpsemalt, mitte halvemale) lahendusele ülemineku reegel;

leitud lahenduse optimaalsuse kontrollimise kriteerium.

Simpleksmeetodi kasutamiseks tuleb lineaarse programmeerimise probleem taandada kanooniline vorm, st. piirangute süsteem tuleb esitada võrrandite kujul.

Kirjanduses on piisavalt detailselt kirjeldatud: esialgse tugiplaani leidmine (esialgne lubatav põhilahendus), ka kunstliku baasmeetodi kasutamine, optimaalse tugiplaani leidmine, ülesannete lahendamine simplekstabelite abil.

3.2. Simpleksmeetodi algoritm.

Vaatleme ZLP lahendust simpleksmeetodil ja esitame selle maksimeerimisülesandega seoses.

1. Ülesande tingimustest lähtuvalt koostatakse selle matemaatiline mudel.

2. Koostatud mudel teisendatakse kanooniline vorm. Sel juhul saab kindlaks teha esialgse võrdlusplaaniga aluse.

3. Ülesande kanooniline mudel on kirjutatud simplekstabeli kujul, nii et kõik vabad liikmed on mittenegatiivsed. Kui esialgne võrdlusplaan on valitud, jätkake sammuga 5.

Simplekstabel: piiranguvõrrandite süsteem ja sihtfunktsioon sisestatakse avaldiste kujul, mis on lahendatud algaluse suhtes. Koefitsiente sisaldav rida objektiivne funktsioon
, kutsus
– sihtfunktsiooni string või string.

4. Leidke esialgne võrdlusplaan, sooritades simpleksteisendusi positiivsete lahutuselementidega, mis vastavad minimaalsetele simpleksseotele ja arvestamata elementide märke.
- jooned. Kui teisenduste käigus tekib 0-rida, mille kõik elemendid, välja arvatud vaba liige, on nullid, siis on ülesande piiranguvõrrandi süsteem ebaühtlane. Kui kohtame 0-rida, milles peale vaba liikme muid positiivseid elemente ei ole, siis pole restriktiivsete võrrandite süsteemil mittenegatiivseid lahendeid.

Nimetame süsteemi (2.55), (2.56) redutseerimise uuele alusele simpleksteisendus . Kui vaadelda simpleksteisendust kui formaalset algebralist tehtet, siis võib märgata, et selle toimingu tulemusena jaotuvad rollid ümber kahe muutuja vahel, mis kuuluvad teatud lineaarsete funktsioonide süsteemi: üks muutuja muutub sõltuvast sõltumatuks ja teine. , vastupidi, sõltumatust ülalpeetavaks. Seda operatsiooni tuntakse algebras kui Jordani väljalangemise etapp.

5. Leitud esialgse toetusplaani optimaalsust uuritakse:

a) kui sees
– reas pole negatiivseid elemente (vaba tähtaega arvestamata), siis on plaan optimaalne. Kui nulle pole, siis on ainult üks optimaalne plaan; kui on vähemalt üks null, siis on optimaalseid plaane lõpmatu arv;

b) kui c
– reas on vähemalt üks negatiivne element, mis vastab mittepositiivsete elementide veerule, siis
;

c) kui sees
- real on vähemalt üks negatiivne element ja selle veerus on vähemalt üks positiivne element, siis saate liikuda uuele võrdlusplaan, optimaalsele lähemal. Selleks tuleb määratud veerg määrata lahutusveeruks, kasutades minimaalset simplekssuhet, leida lahutusrida ja sooritada simpleksteisendus. Saadud võrdlusplaani optimaalsust kontrollitakse uuesti. Kirjeldatud protsessi korratakse kuni optimaalse plaani saamiseni või kuni probleemi lahendamatuse tuvastamiseni.

Aluses sisalduva muutuja koefitsientide veergu nimetatakse lahendamiseks. Seega negatiivse elemendi poolt baasi sisestatud muutuja valimine (või lahendava veeru valimine).
-stringid, pakume suurendavat funktsiooni
.

Baasist välja jäetava muutuja määramine on veidi keerulisem. Selleks koostavad nad vabade liikmete suhted lahendava veeru positiivsete elementide vahel (sellisi seoseid nimetatakse simpleksiks) ja leiavad nende hulgast väikseima, mis määrab välistatud muutujat sisaldava rea ​​(lahutav). Alusest välja jäetud muutuja valik (või lahutusrea valik) vastavalt minimaalsele simpleksseosele tagab, nagu juba kindlaks tehtud, baaskomponentide positiivsuse uues võrdlusplaanis.

Algoritmi punktis 3 eeldatakse, et vabade liikmete veeru kõik elemendid on mittenegatiivsed. See nõue pole vajalik, kuid kui see on täidetud, tehakse kõik järgnevad simpleksteisendused ainult positiivsete lahutuselementidega, mis on arvutuste jaoks mugav. Kui vabade terminite veerus on negatiivsed arvud, valitakse lahendav element järgmiselt:

1) vaata näiteks mõnele negatiivsele vabaterminile vastavat rida – rida ja vali selles negatiivne element ning vastav veerg loetakse lahendavaks (eeldame, et ülesande piirangud on järjepidevad);

2) moodustab vabaterminite veeru elementide seosed vastavate samatähistega lahendava veeru elementidega (simpleksseosed);

3) vali lihtseostest väikseim. See määrab lubava stringi. Olgu see näiteks r-joon;

4) lahutusveeru ja rea ​​ristumiskohast leitakse lahutuselement. Kui element on lubav –stringid, siis pärast simpleksteisendust muutub selle stringi vaba liige positiivseks. Vastasel juhul pöördume järgmises etapis uuesti selle poole - rida. Kui probleem on lahendatav, siis pärast teatud arvu samme ei jää vabade terminite veergu negatiivseid elemente.

Kui teatud tegelik tootmissituatsioon on väljendatud PLP-vormingus, siis lisamuutujatel, mis tuleb mudelisse kanoonilisele vormile teisendamise käigus sisestada, on alati teatud majanduslik tähendus.

Üks optimeerimisülesannete lahendamise meetoditest ( tavaliselt seostatakse miinimumi või maksimumi leidmisega) nimetatakse lineaarset programmeerimist. Lihtne meetod sisaldab tervet rühma algoritme ja meetodeid lineaarse programmeerimise probleemide lahendamiseks. Nimetatakse üks neist meetoditest, mis hõlmab lähteandmete salvestamist ja nende ümberarvutamist spetsiaalsesse tabelisse tabeliline simpleksmeetod.

Vaatleme lahenduse näitel tabeli simpleksmeetodi algoritmi tootmisülesanne, mis taandub maksimaalset kasumit tagava tootmisplaani leidmisele.

Sisendandmed simpleksmeetodi probleemi jaoks

Ettevõte toodab 4 tüüpi tooteid, töödeldes neid 3 masinal.

Ajastandardid (min/tk) toodete töötlemiseks masinates on määratud maatriksiga A:

Masina tööaja fond (min) on määratud maatriksis B:

Iga tooteühiku müügist saadav kasum (RUB/tk) saadakse maatriksiga C:

Tootmisülesande eesmärk

Koostage tootmisplaan, mis maksimeerib ettevõtte kasumit.

Ülesande lahendamine tabeli simpleksmeetodi abil

(1) Tähistagem X1, X2, X3, X4 igat tüüpi toodete kavandatud arvu. Siis soovitud plaan: ( X1, X2, X3, X4)

(2) Kirjutame plaani piirangud võrrandisüsteemi kujul:

(3) Siis on sihtkasum:

See tähendab, et tootmisplaani täitmisest saadav kasum peaks olema maksimaalne.

(4) Saadud tingimusliku ekstreemumi ülesande lahendamiseks asendame võrratuste süsteemi süsteemiga lineaarvõrrandid lisades sellesse täiendavaid mittenegatiivseid muutujaid ( X5, X6, X7).

(5) Aktsepteerigem järgmist võrdlusplaan:

X1 = 0, X2 = 0, X3 = 0, X4 = 0, X5 = 252, X6 = 144, X7 = 80

(6) Sisestame andmed sisse simpleks laud:

Viimasele reale sisestame sihtfunktsiooni koefitsiendid ja selle väärtuse enda vastupidine märk;

(7) Valige sisse viimane rida suurim (modulo) on negatiivne arv.

Arvutame b = N / valitud_veeru_üksused

Valime b arvutatud väärtuste hulgast vähemalt.

Valitud veeru ja rea ​​ristumiskoht annab meile lahendava elemendi. Muudame aluse muutujaks, mis vastab lahendavale elemendile ( X5 kuni X1).

• Lahutav element ise muutub 1-ks.
• Eraldusrea elementide puhul – a ij (*) = a ij / RE ( see tähendab, et jagame iga elemendi lahendava elemendi väärtusega ja saame uued andmed).
• Eraldusvõime veeru elementide puhul lähtestatakse need lihtsalt nulli.
• Tabeli ülejäänud elemendid arvutame ümber ristkülikureegli abil.

a ij (*) = a ij – (A * B / RE)

Nagu näete, võtame praeguse ümberarvutatava lahtri ja lahendava elemendiga lahtri. Need moodustavad ristküliku vastasnurgad. Järgmisena korrutame väärtused selle ristküliku kahe teise nurga lahtritest. See töö ( A * B) jaga lahutuselemendiga ( RE). Ja lahutage praegusest ümberarvutatavast lahtrist ( a ij), mis juhtus. Saame uue väärtuse - a ij (*).

(9) Kontrolli viimast rida uuesti ( c) sees negatiivsete arvude olemasolu. Kui neid pole, on optimaalne plaan leitud, minge aadressile viimane etapp probleemi lahendamine. Kui on, pole plaan veel optimaalne ja simplekstabel tuleb uuesti ümber arvutada.

Kuna viimasel real on jälle negatiivsed arvud, alustame arvutuste uut iteratsiooni.

(10) Kuna viimasel real puuduvad negatiivsed elemendid, siis see tähendab, et oleme leidnud optimaalse tootmisplaani! Nimelt: toodame neid tooteid, mis on kolinud veergu “Bas” - X1 ja X2. Teame iga toodanguühiku tootmisest saadavat kasumit ( maatriks C). Jääb üle korrutada toodete 1 ja 2 leitud tootmismahud kasumiga 1 tüki kohta, saame lõpliku ( maksimum! ) antud tootmisplaani kasum.

VASTUS:

X1 = 32 tk., X2 = 20 tk., X3 = 0 tk., X4 = 0 tk.

P = 48 * 32 + 33 * 20 = 2196 hõõruda.

Galyautdinov R.R.

© Materjali kopeerimine on lubatud ainult siis, kui sellel on otsene hüperlink

. Simpleksmeetodi algoritm

Näide 5.1. Lahendage simpleksmeetodi abil järgmine lineaarse programmeerimise probleem:

Lahendus:

I iteratsioon:

x3, x4, x5, x6 x1,x2. Väljendame põhimuutujaid vabadena:

Vähendame sihtfunktsiooni järgmine vaade:

Saadud ülesande põhjal moodustame esialgse simplekstabeli:

Tabel 5.3

Originaal simplekslaud

				Hindavad suhted

Põhilahenduse definitsiooni kohaselt on vabad muutujad võrdsed nulliga ja põhimuutujate väärtused on võrdsed vabade arvude vastavate väärtustega, st:

3. etapp: PAP piirangute süsteemi ühilduvuse kontrollimine.

Sellel iteratsioonil (tabelis 5.3) ei tuvastata piirangusüsteemi mittevastavuse märki (märk 1) (st ei ole negatiivse vaba arvuga rida (v.a sihtfunktsiooni rida), milles seda poleks olema vähemalt üks negatiivne element (st vaba muutuja negatiivne koefitsient)).

Sellel iteratsioonil (tabelis 5.3) sihtfunktsiooni piiramatuse märki (märk 2) ei tuvastatud (st sihtfunktsiooni real ei ole negatiivse elemendiga veergu (v.a vabade arvude veerg). ), milles poleks vähemalt üht positiivset elementi) .

Kuna leitud põhilahendus ei sisalda negatiivseid komponente, on see lubatav.

6. etapp: optimaalsuse kontroll.

Leitud põhilahendus ei ole optimaalne, kuna optimaalsuse kriteeriumi (märk 4) järgi ei tohiks sihtfunktsiooni real olla negatiivseid elemente ( tasuta number seda joont ei võeta selle tunnuse arvestamisel arvesse). Seetõttu liigume vastavalt simpleksmeetodi algoritmile 8. etappi.

Kuna leitud põhilahend on lubatav, siis otsime lahendavat veergu järgmise skeemi järgi: määrame sihtfunktsiooni real negatiivsete elementidega veerud (v.a vabade arvude veerg). Tabeli 5.3 kohaselt on kaks sellist veergu: veerg “ x1" ja veerg " x2" Sellistest veergudest valitakse see, mis sisaldab sihtfunktsiooni rea väikseimat elementi. Temast saab lubaja. veerg " x2" sisaldab väikseimat elementi (–3) võrreldes veeruga " x1

Lahutusjoone määramiseks leiame vabade arvude positiivsed hinnangulised suhted lahutusveeru elementidega, mis võetakse lahendatuks.

Tabel 5.4

Originaal simplekslaud

Tabelis 5.4 vastab väikseim positiivne hinnanguline seos reale “ x5"Seepärast on see lubatav.

Lubava veeru ja lubamisrea ristumiskohas asuv element loetakse lubavaks. Meie näites on see element, mis asub joone " ristumiskohas x5" ja veerud " x2».

Lahenduselement näitab ühte alust ja ühte vaba muutujat, mis tuleb simplekstabelis vahetada, et liikuda uuele "täiustatud" baaslahendusele. IN antud juhul need on muutujad x5 Ja x2, uues simplekstabelis (tabel 5.5) vahetame need ära.

9.1. Lahutava elemendi transformatsioon.

Tabeli 5.4 eraldusvõime element teisendatakse järgmiselt:

Saadud tulemuse sisestame sarnasesse lahtrisse tabelis 5.5.

9.2. Eraldusvõime stringi teisendamine.

Jagame tabeli 5.4 lahutusrea elemendid selle simplekstabeli lahutuselemendiga, tulemused mahuvad uue simplekstabeli (tabel 5.5) sarnastesse lahtritesse. Resolutsioonistringi elementide teisendused on toodud tabelis 5.5.

9.3. Eraldusvõime veeru teisendamine.

Jagame tabeli 5.4 eraldusvõime veeru elemendid selle simplekstabeli eraldusvõime elemendiga ja tulemus võetakse vastupidise märgiga. Saadud tulemused sobivad uue simplekstabeli sarnastesse lahtritesse (tabel 5.5). Eraldusvõime veeru elementide teisendused on toodud tabelis 5.5.

9.4. Simplekstabeli ülejäänud elementide teisendus.

Ülejäänud simplekstabeli elementide (st elemendid, mis ei asu lahutusreas ja lahutusveerus) teisendamine toimub ristküliku reegli järgi.

Näiteks kaaluge joone ristumiskohas asuva elemendi teisendamist x3" ja veerud "", tähistame seda tingimuslikult " x3" Tabelis 5.4 joonistame mõtteliselt ristküliku, mille üks tipp asub lahtris, mille väärtust me teisendame (st lahtris " x3") ja teine ​​(diagonaaltipp) on lahutuselemendiga lahtris. Ülejäänud kaks tippu (teise diagonaali) on üheselt määratud. Seejärel lahtri teisendatud väärtus " x3" on võrdne selle lahtri eelmise väärtusega, millest on lahutatud murdosa, mille nimetajas on lahutuselement (tabelist 5.4) ja lugejas on kahe teise kasutamata tipu korrutis, st:

« x3»: .

Teiste lahtrite väärtused teisendatakse sarnaselt:

« x 3 x 1»: ;

« x4»: ;

« x4x1»: ;

« x6»: ;

« x 6 x 1»: ;

«»: ;

« x1»: .

Nende ümberkujundamiste tulemusena saime uue simpleks laud(Tabel 5.5).

II iteratsioon:

1. etapp: simplekstabeli koostamine.

Tabel 5.5

Simplex tabelII iteratsioonid

				Hinnanguline suhe

2. etapp: põhilahuse määramine.

Simpleksteisenduste tulemusena saadi uus aluseline lahendus (tabel 5.5):

Nagu näete, on selle põhilahenduse korral sihtfunktsiooni väärtus 15, mis on suurem kui eelmise põhilahenduse puhul.

Tabeli 5.5 tunnuse 1 kohase piirangute süsteemi vastuolu ei ole tuvastatud.

4. etapp: sihtfunktsiooni piirituse kontrollimine.

Tabeli 5.5 kriteeriumi 2 kohase sihtfunktsiooni piiramatust ei selgu.

5. etapp: leitud põhilahenduse vastuvõetavuse kontrollimine.

Kriteeriumile 4 vastav leitud põhilahend ei ole optimaalne, kuna simplekstabeli (tabel 5.5) eesmärkfunktsiooni rida sisaldab negatiivset elementi: –2 (selle rea vaba arvu selle arvestamisel arvesse ei võeta iseloomulik). Seetõttu liigume edasi 8. etapi juurde.

8. etapp: lahutuselemendi määramine.

8.1. Eraldusvõime veeru määratlus.

Leitud põhilahendus on vastuvõetav, määrame sihtfunktsiooni real negatiivsete elementidega veerud (va vabade arvude veerg). Tabeli 5.5 kohaselt on ainult üks selline veerg: “ x1" Seetõttu aktsepteerime seda lubatud kujul.

8.2. Lubamisstringi definitsioon.

Tabelis 5.6 saadud positiivsete hindamissuhete väärtuste järgi on miinimumiks reale " vastav seos. x3" Seetõttu aktsepteerime seda lubatud kujul.

Tabel 5.6

Simplex tabelII iteratsioonid

				Hinnanguline suhe
				3/1=3 – min

9. etapp: simplekstabeli teisendus.

Simplekstabeli (tabel 5.6) teisendused sooritatakse samamoodi nagu eelmises iteratsioonis. Simplekstabeli elementide teisenduste tulemused on toodud tabelis 5.7.

III iteratsioon

Eelmise iteratsiooni simpleksteisenduste tulemuste põhjal koostame uue simplekstabeli:

Tabel 5.7

Simplex tabelIII iteratsioonid

				Hinnanguline suhe

2. etapp: põhilahuse määramine.

Simpleksteisenduste tulemusena saadi uus aluseline lahendus (tabel 5.7):

3. etapp: piirangute süsteemi ühilduvuse kontrollimine.

Tabeli 5.7 tunnuse 1 kohase piirangute süsteemi vastuolu ei ole tuvastatud.

4. etapp: sihtfunktsiooni piirituse kontrollimine.

Tabeli 5.7 kriteeriumi 2 kohase sihtfunktsiooni piiramatust ei selgu.

5. etapp: leitud põhilahenduse vastuvõetavuse kontrollimine.

Leitud põhilahendus vastavalt kriteeriumile 3 on vastuvõetav, kuna see ei sisalda negatiivseid komponente.

6. etapp: leitud põhilahenduse optimaalsuse kontrollimine.

Kriteeriumile 4 vastav leitud põhilahend ei ole optimaalne, kuna simplekstabeli (tabel 5.7) sihtfunktsiooni rida sisaldab negatiivset elementi: –3 (selle rea vaba arvu selle arvestamisel arvesse ei võeta iseloomulik). Seetõttu liigume edasi 8. etapi juurde.

8. etapp: lahutuselemendi määramine.

8.1. Eraldusvõime veeru määratlus.

Leitud põhilahendus on vastuvõetav, määrame sihtfunktsiooni real negatiivsete elementidega veerud (va vabade arvude veerg). Tabeli 5.7 kohaselt on ainult üks selline veerg: “ x5" Seetõttu aktsepteerime seda lubatud kujul.

8.2. Lubamisstringi definitsioon.

Vastavalt tabelis 5.8 saadud positiivsete hindamissuhete väärtustele on miinimumiks reale " vastav seos. x4" Seetõttu aktsepteerime seda lubatud kujul.

Tabel 5.8

Simplex tabelIII iteratsioonid

				Hinnanguline suhe
				5/5=1 – min

9. etapp: simplekstabeli teisendus.

Simplekstabeli (tabel 5.8) teisendused sooritatakse samamoodi nagu eelmises iteratsioonis. Simplekstabeli elementide teisenduste tulemused on toodud tabelis 5.9.

IV iteratsioon

1. etapp: uue simplekslaua ehitamine.

Eelmise iteratsiooni simpleksteisenduste tulemuste põhjal koostame uue simplekstabeli:

Tabel 5.9

Simplex tabelIV iteratsioonid

				Hinnanguline suhe
			–(–3/5)=3/5
			–(1/5)=–1/5
			–(9/5)=–9/5
			–(–3/5)=3/5

2. etapp: põhilahuse määramine.

Simpleksteisenduste tulemusena saadi uus põhilahend vastavalt tabelile 5.9, lahend on järgmine:

3. etapp: piirangute süsteemi ühilduvuse kontrollimine.

Tabeli 5.9 tunnuse 1 kohase piirangute süsteemi vastuolu ei ole tuvastatud.

4. etapp: sihtfunktsiooni piirituse kontrollimine.

Tabeli 5.9 kriteeriumi 2 kohase sihtfunktsiooni piiramatust ei selgu.

5. etapp: leitud põhilahenduse vastuvõetavuse kontrollimine.

Leitud põhilahendus vastavalt kriteeriumile 3 on vastuvõetav, kuna see ei sisalda negatiivseid komponente.

6. etapp: leitud põhilahenduse optimaalsuse kontrollimine.

Leitud põhilahendus vastavalt tunnusele 4 on optimaalne, kuna simplekstabeli (tabel 5.9) sihtfunktsiooni real ei ole negatiivseid elemente (selle tunnuse arvestamisel selle rea vaba arvu ei võeta arvesse) .

7. etapp: lahenduse alternatiivsuse kontrollimine.

Leitud lahendus on unikaalne, kuna sihtfunktsiooni rida (tabel 5.9) ei sisalda null elementi(selle tunnuse arvestamisel selle rea vaba numbrit ei võeta arvesse).

Vastus: vaadeldava ülesande sihtfunktsiooni optimaalne väärtus =24, mis saavutatakse juures.

Näide 5.2. Lahendage ülaltoodud lineaarse programmeerimise probleem tingimusel, et sihtfunktsioon on minimeeritud:

Lahendus:

I iteratsioon:

1. etapp: algse simplekstabeli moodustamine.

Algne probleem lineaarne programmeerimine on määratletud standardvorm. Viime selle kanoonilisele kujule, lisades igasse ebavõrdsuse piirangusse täiendava mittenegatiivse muutuja, st.

Saadud võrrandisüsteemis võtame lubatud (põhi)muutujad x3, x4, x5, x6, siis on vabad muutujad x1,x2. Väljendame põhimuutujaid vabadena.

Kolme kaubagrupi müügiks äriettevõte omab kolme tüüpi piiratud materiaalseid ja rahalisi ressursse summas b 1 = 240, b 2 = 200, b 3 = 160 ühikut. Samal ajal 1 kaubagrupi müügiks 1000 rubla eest. kaubakäibe korral tarbitakse esimest tüüpi ressurssi a 11 = 2 ühikut, teist tüüpi ressurssi a 21 = 4 ühikut, kolmandat tüüpi ressurssi summas 31 = 4 ühikut. 2 ja 3 kaubagrupi müügiks 1000 rubla eest. käivet tarbitakse vastavalt esimest tüüpi ressursile summas a 12 = 3, a 13 = 6 ühikut, teist tüüpi ressurssi summas a 22 = 2, a 23 = 4 ühikut, ressurssi kolmas tüüp summas a 32 = 6, a 33 = 8 ühikut . Kasum kolme kaubagrupi müügist 1 tuhande rubla eest. käive on vastavalt c 1 = 4, c 2 = 5, c 3 = 4 (tuhat rubla). Määrata kaubanduskäibe planeeritav maht ja struktuur nii, et kasum kaubandusettevõte oli maksimum.

Käibe planeerimise otsesele probleemile lahendatakse simpleksmeetodil, koostada kahekordne probleem lineaarne programmeerimine.
Installige muutujate konjugeeritud paarid sirge ja kahekordne probleem.
Muutujate konjugeeritud paaride järgi saame otsese ülesande lahendusest topeltprobleemi lahendus, milles seda toodetakse ressursside hindamine, kulutatud kaupade müügile.

Probleemi lahendamine simpleksmeetodi abil

Olgu x 1, x 2, x 3 vastavalt 1, 2, 3 rühma müüdud kaupade arv tuhandetes rublades. Siis matemaatiline mudelülesandel on vorm:

F = 4 x 1 + 5 x 2 + 4 x 3 -> max

0)))(~)" title="delim(lbrace)(maatriks(4)(1)((2x_1 + 3x_2 + 6x_3= 0)))(~)">!}

Lahendame simpleksmeetodi.

Toome sisse täiendavad muutujad x 4 ≥ 0, x 5 ≥ 0, x 6 ≥ 0, et muuta võrratused võrdsusteks.

Võtame aluseks x 4 = 240; x 5 = 200; x 6 = 160.

Sisestame andmed sisse simpleks laud

Simplex tabel nr 1

Objektiivne funktsioon:

0 240 + 0 200 + 0 160 = 0

Arvutame hinnangud järgmise valemi abil:

Δ 1 = 0 2 + 0 4 + 0 4 - 4 = - 4
Δ 2 = 0 3 + 0 2 + 0 6 - 5 = - 5
Δ 3 = 0 6 + 0 4 + 0 8 - 4 = - 4
Δ 4 = 0 1 + 0 0 + 0 0 - 0 = 0
Δ 5 = 0 0 + 0 1 + 0 0 - 0 = 0
Δ 6 = 0 0 + 0 0 + 0 1 - 0 = 0

Kuna on negatiivseid hinnanguid, pole plaan optimaalne. Madalaim punktisumma:

Toome baasi sisse muutuja x 2.

Defineerime baasist lähtuva muutuja. Selleks leiame x2 veeru jaoks väikseima mittenegatiivse suhte.

= 26.667

Väikseim mittenegatiivne: Q 3 = 26,667. Muutuja x 6 tuletame baasist

Jagage kolmas rida 6-ga.
1. realt lahutage 3. rida, korrutatuna 3-ga
2. realt lahutame 3. rea korrutatuna 2-ga

Arvutame:

Me saame uus laud:

Simplex tabel nr 2

Objektiivne funktsioon:

0 160 + 0 440/3 + 5 80/3 = 400/3

Arvutame hinnangud järgmise valemi abil:

Δ 1 = 0 0 + 0 8/3 + 5 2/3 - 4 = - 2/3
Δ 2 = 0 0 + 0 0 + 5 1 - 5 = 0
Δ 3 = 0 2 + 0 4/3 + 5 4/3 - 4 = 8/3
Δ 4 = 0 1 + 0 0 + 5 0 - 0 = 0
Δ 5 = 0 0 + 0 1 + 5 0 - 0 = 0
Δ 6 = 0 (-1)/2 + 0 (-1)/3 + 5 1/6 - 0 = 5/6

Kuna on negatiivne hinnang Δ 1 = - 2/3, ei ole plaan optimaalne.

Toome baasi sisse muutuja x 1.

Defineerime baasist lähtuva muutuja. Selleks leiame veeru x 1 väikseima mittenegatiivse suhte.

Väikseim mittenegatiivne: Q 3 = 40. Muutuja x 2 tuletame baasist

Jagage 3. rida 2/3-ga.
2. realt lahutage 3. rida, korrutatuna 8/3-ga

Arvutame:

Saame uue tabeli:

Simplex tabel nr 3

Objektiivne funktsioon:

0 160 + 0 40 + 4 40 = 160

Arvutame hinnangud järgmise valemi abil:

Δ 1 = 0 0 + 0 0 + 4 1 - 4 = 0
Δ 2 = 0 0 + 0 (-4) + 4 3/2 - 5 = 1
Δ 3 = 0 2 + 0 (-4) + 4 2 - 4 = 4
Δ 4 = 0 1 + 0 0 + 4 0 - 0 = 0
Δ 5 = 0 0 + 0 1 + 4 0 - 0 = 0
Δ 6 = 0 (-1)/2 + 0 (-1) + 4 1/4 - 0 = 1

Kuna negatiivseid hinnanguid pole, on plaan optimaalne.

Probleemi lahendus:

Vastus

x 1 = 40; x2 = 0; x 3 = 0; x 4 = 160; x 5 = 40; x6 = 0; F max = 160

See tähendab, et on vaja müüa esimest tüüpi kaupu 40 tuhande rubla ulatuses. 2. ja 3. tüüpi kaupu ei ole vaja müüa. Samal ajal maksimaalne kasum on F max = 160 tuhat rubla.

Topeltprobleemi lahendus

Kahekordsel probleemil on vorm:

Z = 240 a 1 + 200 a 2 + 160 a 3 -> min

Title="delim(lbrace)(maatriks(4)(1)((2a_1 + 4a_2 + 4a_3>=4) (3a_1 + 2a_2 + 6a_3>=5) (6a_1 + 4a_2 + 8a_3>=4) (y_1, y_2, y_3>= 0)))(~)">!}

Toome sisse täiendavad muutujad y 4 ≥ 0, y 5 ≥ 0, y 6 ≥ 0, et muuta võrratused võrdsusteks.

Otsese ja duaalse probleemi muutujate konjugeeritud paarid on järgmisel kujul:

Otsese ülesande viimasest simplekstabelist nr 3 leiame lahenduse duaalülesandele:

Z min = Fmax = 160;
y1 = A4 = 0; y2 = A5 = 0; y3 = A6 = 1; y4 = Δ1 = 0; y5 = A2 = 1; y6 = A3 = 4;

Lineaarse programmeerimise probleemid. See on vaadeldavat protsessi iseloomustavas järjestikuses konstruktsioonis. Lahendus jaguneb kolmeks põhietapiks: muutujate valik, piirangute süsteemi konstrueerimine ja eesmärgifunktsiooni otsimine.

Selle jaotuse alusel saab probleemitingimuse ümber sõnastada järgmiselt: sihtfunktsiooni ekstreemum Z(X) = f(x1, x2, … ,xn) → max (min) ja vastavad muutujad, kui on teada, et need täitma piirangute süsteemi: Φ_i ( x1, x2, … ,xn) = 0, kui i = 1, 2, …, k;Φ_i (x1, x2, … ,xn)) 0 kui i = k+1, k+ 2, …, m.

Piirangute süsteem tuleb viia kanoonilisele kujule, s.o. lineaarvõrrandi süsteemile, kus muutujate arv rohkem numbrit võrrandid (m > k). Selles süsteemis on kindlasti muutujaid, mida saab väljendada teiste muutujate kaudu ja kui see nii ei ole, siis saab neid kunstlikult sisestada. Sel juhul nimetatakse esimesi baasiks või kunstlik alus, ja teised on tasuta.

Mugavam on kasutada simpleksmeetodit konkreetne näide. Olgu lineaarne funktsioon f(x) = 6x1 + 5x2 + 9x3 ja piirangute süsteem: 5x1 + 2x2 + 3x3 ≤ 25 x1 + 6x2 + 2x3 ≤ 20, et leida maksimaalne väärtus funktsioonid f(x).

Lahendus Esimeses etapis määrake absoluutselt suvaliselt võrrandisüsteemi esialgne (referents)lahend, mis peab antud piirangute süsteemi rahuldama. Sellisel juhul on vajalik kunstliku kasutuselevõtt, s.t. põhimuutujad x4, x5 ja x6: 5x1 + 2x2 + 3x3 + x4 = 25 x1 + 6x2 + 2x3 + x5 = 4x1 + 3x3 + x6 = 18;

Nagu näete, on võrratused muudetud võrdsusteks tänu lisatud muutujatele x4, x5, x6, mis on mittenegatiivsed suurused. Seega olete viinud süsteemi kanoonilisele kujule. Muutuja x4 sisaldub esimeses võrrandis koefitsiendiga 1 ja teises võrrandis koefitsiendiga 0, sama kehtib ka muutujate x5, x6 ja vastavate võrrandite puhul, mis vastab aluse definitsioonile.

Olete süsteemi koostanud ja leidnud esialgse võrdluslahenduse – X0 = (0, 0, 0, 25, 20, 18). Edaspidiste arvutuste optimeerimiseks esitage nüüd muutujate koefitsiendid ja võrrandite vabad liikmed (= märgist paremal olevad numbrid) tabelina (vt joonist).

Simpleksmeetodi põhiolemus on viia see tabel kujule, kus kõik rea L numbrid on mittenegatiivsed. Kui selgub, et see on võimatu, siis süsteemil pole optimaalne lahendus. Alustuseks valige kõige rohkem minimaalne element sellel real on -9. Number on kolmandas veerus. Teisendage vastav x3 muutuja baasmuutujaks. Selleks jagage joon 3-ga, nii et lahtri lõpus on 1.

Nüüd vajate lahtreid ja 0-le pööramiseks. Selleks lahutage kolmanda rea ​​vastavatest numbritest 3. Teise rea elementidest - kolmanda rea ​​elemendid, korrutatuna 2-ga. rea L elemendid - korrutatuna (-9). Olete saanud teise võrdluslahendi: f(x) = L = 54, kus x1 = (0, 0, 6, 7, 8, 0).